
嗨,habrozhiteli! 本书基于蒂姆·拉夫加登(Tim Rafgarden)在Coursera和斯坦福·拉古尼塔(Stanford Lagunita)上开设的在线算法课程,这些课程的出现得益于他多年来在斯坦福大学为学生提供的讲座。
算法是计算机科学的灵魂。 您无法没有它们,它们无处不在-从网络路由和基因组计算到密码学和机器学习。 “完美算法”将使您成为真正的专业人士,他们将在雇用任何IT公司时设定任务并在生活中和面试中熟练地解决任务。 蒂姆·拉夫加登(Tim Rafgarden)将讨论渐近分析,big-O表示法,分治法,随机化,排序和选择。 本书面向已经有编程经验的读者。 您将进入一个新的高度,以了解全局,了解低层次的概念和数学上的细微差别。
* 6.3。 DSelect算法
RSelect算法在每个输入的线性时间内执行,其中数学期望与该算法执行的随机选择相关。 线性选择是否需要随机化? 在本节以及进一步的内容中,将使用确定性线性算法解决选择问题,以解决此问题。
对于排序任务,O(n log n)随机QuickSort算法的平均运行时间与确定性MergeSort算法相同,并且QuickSort和MergeSort这两种算法都是实用的实用算法。 另一方面,尽管本节中描述的确定性线性选择算法在实践中可以很好地工作,但是它不能与RSelect算法竞争。 发生这种情况的原因有两个:由于DSelect算法的运行时间中的常数常数较大,以及该算法执行的工作与附加RAM的分配和管理相关联。 尽管如此,算法中的想法是如此酷,以至于我不禁告诉您它们。
6.3.1。 绝妙的主意:中位数的中位数
RSelect算法之所以快速,是因为随机支持元素很有可能会非常好,从而在分离后对输入数组进行近似平衡的拆分,而且,相当好的支持元素也会迅速发展。 如果不允许我们使用随机化,那么如何在不做太多工作的情况下计算出一个很好的参考元素呢?
确定性线性选择中的巧妙想法是使用“中位数中位数”作为真实中位数的替代。 该算法将输入数组的元素视为运动队,并在两轮比赛中举行淘汰赛,冠军是支持者; 另请参见图。 6.1。
第一个回合是一个分组阶段,输入数组中位置1–5的元素为第一组,位置6–10中的元素为第二组,依此类推。 由五个元素组成的组的第一轮获胜者定义为元素的中位数(即第三小)。 既然有
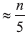
五个元素组成的组,有
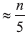
首批获奖者。 (和往常一样,为简单起见,我们忽略了分数。)锦标赛冠军定义为第一轮获胜者的中位数。
6.3.2。 DSelect算法的伪代码
如何实际计算中位数? 淘汰赛第一阶段的实施很简单,因为中位数的每次计算仅包含五个元素。 例如,每个这样的计算都可以通过蛮力执行(对于五种可能性中的每一种,请详细检查它是否是中间元素),也可以使用我们关于分类问题的信息来进行(6.1.2节)。 为了实施第二阶段,我们计算
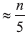
第一轮的获胜者递归。
第1–2和6–13行与RSelect算法相同。 第3至5行是该算法的唯一新部分; 他们计算输入数组的中位数,替换RSelect算法中的行,后者随机选择参考元素。
第3行和第4行计算淘汰赛第一轮的获胜者,其中五个元素的每组的中间元素使用蛮力法或排序算法计算,然后将这些获胜者复制到新的数组C中。第5行通过递归计算数组C的中位数来计算锦标赛的冠军; 因为C有一个长度(暂定)
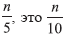
数组C的第4个序数统计量。算法的任何步骤均不使用随机化。
6.3.3。 了解DSelect算法
在计算参考元素时递归调用DSelect算法似乎是危险的循环。 要了解发生了什么,我们首先指定递归调用的总数。
正确答案是:(c)。 丢弃基本情况和满意情况(在这种情况下,参考元素是必需的订单统计信息),DSelect算法进行两次递归调用。 要了解原因,请不要过度使用; 只需逐行检查DSelect算法伪代码。 第5行有一个递归调用,第11或13行有另一个递归调用。
关于这两个递归调用,存在两个令人困惑的常见问题。 首先,RSelect算法仅进行一个递归调用是否不是事实,它为什么比我们的排序算法运行得更快? DSelect不会通过进行两个递归调用来放弃此改进吗? 6.4节显示,由于第5行的额外递归调用只能解决一个相对较小的子任务(原始数组中有20%的元素),因此我们仍然可以保存线性分析。
其次,两个递归调用起着根本不同的作用。 第5行进行递归调用的目的是为当前递归调用确定一个好的参考元素。 第11或13行上的递归调用的目标是通常的目标-递归解决当前递归调用留下的较小的剩余任务。 但是,DSelect算法中的递归结构完全遵循我们研究的所有其他分而治之算法的传统:每个递归调用都会进行少量后续的递归调用,并带有严格更精细的子任务,并且还要做一些额外的工作。 如果我们不担心诸如MergeSort或QuickSort之类的算法会永远运行,那么我们就不必担心DSelect算法。
6.3.4。 DSelect算法运行时
DSelect算法不仅仅是一个定义明确的程序,它可以在有限的时间内完成-它以线性时间运行,仅在恒定因子上完成比读取输入数据所需的更多工作。
定理6.6(DSelect算法的运行时间)。 对于长度n≥1的每个输入数组,DSelect算法的运行时间为O(n)。
与RSelect算法的运行时间原则上不超过Θ(n2)不同,DSelect算法的运行时间始终等于O(n)。 但是,实际上,您应该更喜欢RSelect而不是DSelect,因为前者在同一位置工作,并且定理6.1中平均运行时间“ O(n)”中隐藏的常数小于定理6.6中隐藏的常数。
»这本书的更多信息可以
在出版商的网站上找到»
目录»
摘录对于Khabrozhiteley优惠券20%的折扣-
算法支付纸质版本的书后,将通过电子邮件发送该书的电子版本。
PS:这本书的成本的7%将用于新计算机书籍的翻译,移交给印刷厂的书籍清单在
此处 。