🤱🏼 🧝🏻 🏧 在量子化学方面的Muon催化。第一部分：普通氢气与介子氢 🧚🏽 🔐 🐃

Mnogabukaff认为，量子化学考虑了μ子催化的原理：μ子到底如何降低所需等离子体的温度。分两部分。

第一部分的实质用一个句子表达：μ子比电子重，因此更难将其从质子上撕下来。

但是，那些希望查看分子式，图表并看到应用于最简单（准）原子的量子化学概念实质的人，在猫之下也很受欢迎。

第二部分在此链接上可用。

引言

众所周知，人类的能源消耗量每年都在增长：我们每个人都有更多的小玩意，我们必须四处走动，而我们自己也不少。因此，我们一直在思考，在哪里获取更多的能量，在哪里节省这种能量。

热核聚变（TS）是当前主要能源（煤炭，天然气，水力发电厂和核能）的一种可能替代方案。实际上，这是邪恶核能的好孪生兄弟， ~~关于沙皇炸弹，最不重要的是~~ ：将光核融合成重核，而不是将TS中的核聚变反应用作能量来源。一切似乎都很好：由于TS，我们所有的能源都以某种方式出现了，因为它在恒星中（包括在太阳内部）流动并用作光和热的源，因此所有光合作用都会发生，所有江风拂面。还要感谢TS，我们有一堆比氦重的元素（包括碳=煤，石油，天然气和铀）。
假定的主要合成反应是不同氢同位素（pro

${} _ {1} ^ {1} \ mathrm {H}$ 氘

${} _ {1} ^ {2} \ mathrm {H}$ 和tri

${} _ {1} ^ {3} \ mathrm {H}$ ）问题在于，要以自持模式启动车辆，您需要极高的温度。恒星没有问题，但是在地面条件下，这样的要求仍然是阻碍每个出口中环境友好的热核聚变产生的电流的障碍。降低温度的一种方法是muon催化。维琪告诉我们，μ子（

亩

$\亩^-$ 如此不稳定的重电子克隆（

$e ^-$ ）：它比电子重207倍，寿命仅为2.2微秒。但是，假设将此类粒子添加到发生TS的系统中，将能够降低融合新核所需的最低等离子体温度。而且由于在某些合成反应过程中会形成μ子，而不是使粒子衰减，所以应该出现新的粒子，这些粒子将继续~~参与炼金术~~燃烧氢和其他元素，并形成较重的元素。在氢的通常形式与电子被介子取代的形式之间的差异，涵盖了介子催化的全部本质。并且要看到这一点，我们需要转向量子化学及其概念，我们将要做。在这一部分中，我们将重点介绍氢原子的差异（

$\ mathrm {H ^ \ cdot = p ^ + e ^-}$ ）从其muon对应项（

$\ mathrm {p} ^ + \ mu ^-$ ），其中电子被一个介子取代。

飞越质子的巢...

几个常用词

氢原子。每个人都讨论它，并在学校的物理和化学班上进行学习，因此我们将讨论用介子取代电子如何影响其性质（能量和轨道类型）。我们从两个一般角度考虑这些粒子：

变态的（所谓的旧量子力学）
并且从普通量子力学的角度来看。

第一个考虑因素适用于学童，第二个考虑因素要求对高等数学有更深入的了解。

玻尔轨道

实际上，旧的量子力学是试图使经典力学适应描述不服从它的系统的尝试。尽管有一个完整的描述，但这种方法还是有缺陷的（我们将在下一节中讨论），它是重要且有趣的，同时异常简单。

首先，是通过旧的量子力学，物理学家设法发现了量子系统的问题，因此，从历史的角度来看，这一步骤对于改变物理学的范式是必要且重要的。
其次，玻尔对由两个带正电和负电的氢原子构成的类氢原子问题的解决方案可以解释实验观察结果，并将整个观察到的氢谱动物园串联起来。这一决定的破坏性版本使玻尔（Bohr）获得了1922年诺贝尔奖，我们将在这里考虑。

但是为了解决该问题，我们必须记住在经典情况下如何描述粒子的运动。这是物理学校的课程，但是如果有人忘记了，您可以在这里刷新您的记忆：

经典力学中如何描述质点运动？

我们通常将一个质点模型与一个粒子关联：一种无结构的物体，我们可以在其中测量其位置（

$x$ ）和速度（

点

$v = \ frac {dx} {dt} = \点{x}$ ，来自“ 速度 ”），即随着时间的流逝改变位置

$t$ 。这种点的运动描述的本质非常简单：如果我们知道某个初始时间点的位置/速度

$t_0$ ，我们可以预测其他任何时间点

$t$ ，并且此刻她将以多快的速度移动。而且，我们无所不能，不仅可以展望未来，甚至可以回顾过去：当下

$t$ 也许之前

$t_0$ （

$t <t_0$ ），根据魔术类型的所有定律，预测本身必须基于某种咒语，并且每位学习物理学的学校学者都知道这一点。这是牛顿的第二定律，仅是二阶微分方程式中的强萨满教：

$F = ma \。$ 在这里，通常， a是加速度（来自“ 加速度 ”），是速度的一阶时间导数（

$a = \ frac {d v} {dt}$ ），或第二个坐标（

$a = \ frac {d ^ 2 x} {dt ^ 2}$ ，因此是二阶）。但是除了加速这种法术之外，我们还有柔道的另一个奇迹，那就是柔道如何运动：这就是力F。众所周知，她描述了控制粒子运动的东西。所谓的一种特殊的力就是所谓的两种最基本的相互作用（万有引力，无心和电磁）。势力。在这种情况下，可以引入另一个称为势能的实体（我们将用字母V表示），该实体将指导不同系统的转换。在最底端，要预测物质点的运动，我们需要（除了其特征，例如质量和电荷）：

初始速度和位置
以力F或什至更好的势V的形式表示的支配它的定律，它将赋予牛顿第二定律以力 $F（x）=-\ frac {dV} {dx}（x）$ 。

根据这些数据，将其全部代入方程式

$F = ma$ 我们将收到粒子的轨迹：粒子在每个时刻的位置和速度值。这就是我们描述世界中我们容易观察到的运动所需要的。

让我们继续执行任务。因此，根据库仑定律，我们有两个带相反电荷的粒子相互吸引，即吸引的势能是

$V（R）= \ overbrace {\ frac {1} {4 \ pi \ varepsilon_0}} ^ {k} \ frac {q_1 q_2} {R} = k \ frac {q_1 q_2} {R}$ 其中R是粒子之间的距离，

$q_i$ -在氢原子和粒子的情况下带电

$\ mathrm {p} ^ + \ mu ^-$ 他们是平等的

$+ e \约+1.6 \乘以10 ^ {-19}$ CL表示质子和

$-e$ 电子和介子，以及

$\ varepsilon_0$ -电常数。由于电荷相反，势能随着粒子之间距离的减小而减小（即在接近过程中），这意味着质子和电子/介子相互吸引。

上图显示了这种情况。但是在某个地方我们看到了类似的系统，对吗？实际上，在我们生活的这些对中的一个对上：太阳+地球或地球+月亮，或地球+ ISS-这也是两个粒子，它们被牛顿定律表示的相似电势吸引：

$V（R）= -G \ frac {m_1 m_2} {R}$

其中G是重力常数，并且

$m_i$ -群众。

质子比电子重1836倍，并且由于介子比电子重207倍，因此质子几乎比介子重9倍。在这两种情况下，我们都有“重粒子+轻粒子”系统，因此我们近似地认为电子/介子围绕质子旋转。当然，在以下情况下，此假设的准确性

$\ mathrm {p} ^ + \ mu ^-$ 氢原子比氢原子的氢原子数要低得多，但是为说明起见，它是非常合适的。在太阳+地球的情况下，地球+ ISS通常使用相似的近似值。

我们对一个稳定的系统感兴趣，在这个稳定的系统中任何地方都不会掉下来，氢原子如果保持不变会存在很长时间。

对于太阳系所有类似物，我们都知道这种运动，对于地球+ ISS对来说，它们甚至是显而易见的：它们是稳定的轨道，在该轨道上，台站以足以不坠落的速度绕地球运动。该速度称为第一宇宙速度，即我们需要氢原子/它的μ子对应物的第一宇宙速度。通过学校公式很容易找到它（请参见上图）。

在半径为R的圆形轨道上移动时（在图中以

$a_0$ ，很快我们就可以做到这一点）您必须有速度

$v$ 。可以想象每时每刻有两个作用在绕圆飞行的粒子上的力垂直于速度矢量：

库仑引力指向中心，根据力的定义 $F =-\ frac {dV} {dR}$ 等于
$F_ \ text {K} = -k \ frac {e ^ 2} {R ^ 2}$
（假的）离心力抵消了它的作用，它试图增大轨道的半径R ，其表达式为
$F_ \文本{q} = \ frac {mv ^ 2} {R}$

其中， m是电子/介子（质子的天然卫星）的质量。

轻粒子不会碰撞成重粒子的条件是，垂直于粒子运动方向的这些力的总和应为零（

$F_ \ mathrm {K} + F_ \ mathrm {q} = 0$ ），这意味着我们得到了等式

$\ frac {mv ^ 2} {R} = k \ frac {e ^ 2} {R ^ 2}$

因此，我们得到了在轨道R的半径处以质量m飞行电子/介子的速度，以免撞到质子上：

${v} = \ sqrt {k \ frac {e ^ 2} {mR}}$

如果电子/μ子不带电，一切都会受到伤害，并且带电粒子在圆周运动时会发射电磁波（这称为辐射摩擦），这会使这种系统变得不稳定：电子/μ子会在旋转过程中发光，结果，它失去了能量并缩小了轨道的半径，最终它落在了质子上，所有东西都变成了白色的蓬松动物。但是，显然不会发生这种情况，这意味着某些小粒子的行为应该与电子/μ子这样的粒子有根本的不同。

实际上，尼尔斯·玻尔（Niels Bohr）也提出了一个非常愚蠢的假设（当时）。他承认存在一定半径的轨道，在该轨道上氢原子不发射任何东西。现在的问题是如何找到这些轨道。为简单起见，我们将在Bohr之前使用成就： de Broglie波长的表达式：

$\ lambda = \ frac {h} {p} = \ frac {h} {mv}$

历史背景

de Broglie公式是在1920年代初期（1923-1924）获得的， Bohr在1913年描述了氢原子。

假定物质（粒子）也具有波属性，并且可以将它们赋予一定的波长，这由de Broglie公式给出。然后，为了使圆周上的运动在时间上保持静止（成为驻波），要求轨道的长度（

$L = 2 \ pi R$ ）适合整数个波。

然后，电子/μ子的波动就可以这样表示（摘自Wiki ）：

用公式的语言表示为：

$2 \ pi R = n \ lambda = n \ frac {h} {mv}$

在这里代入上面获得的第一宇宙质子速度，我们得到方程

$2 \ pi R = \ frac {nh} {m} \ sqrt {\ frac {mR} {ke ^ 2}}$ 。双方都平方了，我们得到第n个固定电子/μ子轨道半径的表达式：

$R_n = n ^ 2 \左（\ overbrace {\ frac {h} {2 \ pi}} ^ {\ hbar} \ right）^ 2 \ cdot \ frac {1} {mk e ^ 2} = \ frac { n ^ 2 \ hbar ^ 2} {mk e ^ 2}$

在这里

$n = 1,2,3，\点$ （我们对要铺设的波浪数没有限制），并且

$\ hbar$ -这就是所谓的降低普朗克常数。我们堆叠的波越多，轨道半径越大。在电子的情况下，最小半径为（ n = 1）（即m等于电子的质量m _e ），这种半径称为玻尔半径，称为K.O。上图）：

$a_0 = R_0 = \ frac {\ hbar ^ 2} {m_ \ mathrm {e} ke ^ 2}$

替换数字（ ħ = 1.054×10 ^–34 J·s， m _e = 9.109×10 ^-31 kg， k = 8.99×10 ⁹ N·m ² ·C ^-2和e = −1.602×10 ^-19 C）值a ₀ = 5.29×10 ^-11 m或0.529埃（Å）。

埃是多少？

1Å= 10 ^-10 m。这很小。

在计算过程中，我们顺便引入了一个新实体：数字

$n = 1,2,3，\点$ 它决定了波数和

$\ Rightarrow$ 轨道半径，甚至电子在轨道上的速度。这个数字是学校里每个人都知道的：这是类氢原子最重要的量子数。我们将在下一节中更详细地讨论这一点，但是现在您可以尝试找到每个级别的能量。

据我们了解，一个封闭系统的能量（毫无疑问，我们的类氢原子就是这样）由两部分组成：

从动能 $T = \ frac {mv ^ 2} {2}$ ，
和潜力，在我们的案例中是库仑定律所赋予的 $V = \ frac {ke ^ 2} {R}$ 。

我们用它们的轨道速度和半径替换为选定的主体数n 。我们已经写出了半径，但是速度看起来像

$v_n ^ 2 = \ frac {k e ^ 2} {m R_n} = \ frac {k ^ 2 e ^ 4} {n ^ 2 \ hbar ^ 2}$ 。

然后

$T_n = \ frac {m v_n ^ 2} {2} = \ frac {m} {2} = \ frac {m k ^ 2 e ^ 4} {2 n ^ 2 \ hbar ^ 2}$ 。有潜力，一切都变得更简单：

$V_n =-\ frac {ke ^ 2} {R_n} =-\ frac {m k ^ 2 e ^ 4} {n ^ 2 \ hbar ^ 2}$ 。总结这些贡献，我们得到一个氢原子的总能量：

$E_n = T_n + V_n =-\ frac {m k ^ 2 e ^ 4} {2 n ^ 2 \ hbar ^ 2}$

这个公式在证明量子力学的正确性方面起着重要作用，因为在氢原子的光谱中观察到了许多谱线（莱曼，巴尔默，帕申等）。有了一个公式和一个简单的模型，就可以一次对它们全部进行解释，这是一个令人信服的论点，赞成承认玻尔的思想。

从这个最简单的模型中榨出所有汁液之后，我们可以从诚实的量子力学的角度出发，对问题进行正确的考虑。

类氢原子的轨道

其次，更重要的是什么是量子力学以及它是如何工作的。可以从各种来源记住这一点。我建议：

哈勃（Habr）发表的一篇文章：《量子力学》。理论上的最小值” （伦纳德·萨斯金德和阿里·弗里德曼同名书籍），
MFTIshnogo老师MG的精彩著作《如何理解量子力学》伊凡诺娃（可从链接下载），
在选择的dxdy论坛上，有很多帖子很好地解释了量子组的本质，
关于Lurke的非常合适的评论和历史文章，
好吧，所有垃圾也可以在Internet上找到。
VK的量子化学网络手册。

但是，这里还压缩了一些必要的东西：

量子力学如何描述粒子运动？

在量子力学中，不能使用轨迹描述粒子的运动（表示为物质点，即无结构的小垃圾）。这禁止了非常著名的海森堡不确定性原理：

$\ Delta x \ cdot \ Delta p \ geq \ frac {\ hbar} {2}$

在哪里

$\ Delta x$ 是测量粒子坐标的误差，并且

$\ Delta p$ -测量粒子动量的误差，与速度相关

$p = MV$ 。实际上，这种不等式表示：如果您非常精确地测量粒子的位置（误差

$\ Delta x$ 小），则此板在测量粒子动量时将是一个巨大的错误

$\ Delta p$ （以及速度），反之亦然。并以降低的普朗克常数ħ = 1.054571800（13）×10 ^-34 J·s表示这种关节精度的下限，这与通常的普朗克常数h为

$h = 2 \ pi \ hbar$ 。如您所见，该值非常小，因此，在我们的世界中，在常规仪器（测速仪，直尺等）的测量精度极限下，我们不会感到这种不平等的下限，因此在我们看来，一切都可以用任何准确性。
但是对于小而轻的粒子，例如电子和介子，无论我们如何努力，都不可能随时查明胡说八道的飞行地点和飞行速度。

实际上...

有量子力学的形式主义（形式主义），其中一种或另一种存在轨迹。最明显的例子是：

理查德·费曼（Richard Feynman）的轨迹上的积分技术，其中每个粒子从点“ A”移动到点“ B”时，都会（以不同程度）通过所有可能和不可能的轨迹，
De Broglie-Bohm导波的解释，在该导波中，每个粒子都像经典力学中那样仅沿一条路径运动，尽管除了普通力之外，该路径还由所谓的力来引导由粒子的波函数产生的量子力。

自然地，在两种情况下，所有结果和结论都与标准波量子力学完全相同，我们将在下文中讨论。特别是，海森堡不确定性原则不会在任何地方消失，它只是获得了不同的语义。
关于这些版本的量子力学的更多信息，可以在M. G. Ivanov的书“如何理解量子力学”中找到。

因此，为了描述量子物体的运动，需要一种新的语言和一种新的事物观，并在经过多次折磨和大量不同程度的成功尝试之后，于1926年由ErwinSchrödinger

（他的个人生活非常有趣）

Schrödinger一生只有一个妻子，这并没有阻止他或她拥有一堆情人。特别是，他与一个年轻（可能未成年）的恋人在度假时在阿尔卑斯山得出了他著名的方程式。

他得出了著名的方程，描述了任何量子系统的动力学：

$i \ hbar \ frac {\部分\ psi} {\部分t} = \帽子{H} \ psi$

除了粒子轨迹，我们还有一个新实体：波动函数

$\ psi$ 是一个复杂的（通常情况下）函数，仅取决于粒子的坐标和时间。

但是，这不是必需的。

波函数可以同时取决于粒子的坐标

$\磅/平方英寸（x）$ （此版本称为坐标表示），并且来自脉冲

$\磅/平方英寸（p）$ ，这种形式称为冲动表示。无论您选择哪种想法，它们都反映出完全相同的状态。从一种表示形式到另一种表示形式的过渡是通过傅立叶变换进行的。

量子力学的本质就在于此本质：代替准确地预测粒子的任何其他物理量的位置/速度/，我们只能准确地确定特定测量结果的概率，仅此而已。测量结果本身将是随机的，但是如果我们采用大量相同的系统并对一定量的物理量进行一堆测量，则统计结果将与我们的预测一致，但与古典物理学中的特定测量结果不一致，但与不同测量的概率一致。

特别是一次发现一个粒子的概率

$t$ 在范围内

$x \ in [x_0，x_0 + \ delta x]$ 大约相等

$\ psi ^ *（x_0，t）\ cdot \ psi（x_0，t）\ cdot \ delta x = | \ psi（x_0，t）| ^ 2 \ cdot \ delta x$ 其中“ *”代表复杂的共轭。
换句话说，数量

$| \ psi | ^ 2$ （波动函数模的平方）是粒子位置分布的概率密度，即，大致来说，粒子在空间中的“拖尾”现象。自然地，从这个意义出发，

$\ int \极限_ {-\ infty} ^ {+ \ infty} | \ psi（x）| ^ 2 dx = 1$ ，因为至少在某处找到粒子的总概率必须等于1。

但是，仅对于粒子的位置而言，一切都如此简单。在一般情况下，所有物理上可测量的量都以特殊的形式表示：运算符。这些运算符在顶部用大写字母表示，即如果我们有一些经典的价值

，那么它的量子模拟将是运算符

$\帽子{A}$ 。

实际上，运算符是需要用wave函数完成的一组转换的集合，它写为

$\帽子{A} \ psi$ 。

例如：

坐标运算符 $x$ 是的 $\帽子{x} = x$ 因此，该运算符对ψ的作用只是乘以坐标值本身，即 $\帽子{x} \ psi（x）= x \ psi（x）$ ，
脉冲算子 $p$ 是 $\ hat {p} =-i \ hbar \ frac {d} {dx}$ 因此，当它作用于波动函数时，结果将是波动函数的导数（ $\ hat {p} \ psi（x）= -i \ hbar \ frac {d \ psi（x）} {dx} = -i \ hbar \ psi'（x）$ ）

所有其他物理量都通过动量和坐标以一种或另一种方式表示（

${A} = A（x，p）$ ），而他们的运算子可通过替换获得

$\ hat {x}，\ hat {p}$ 成经典的表达方式（

$\ hat {A} = A（\ hat {x}，\ hat {p}）$ ）
以及操作员指定的物理量A的平均值

$\帽子{A}$ 如果系统处于波动函数描述的状态

$\磅/平方英寸（x）$ 计算为

$\ int \极限_ {-\ infty} ^ {+ \ infty} \ psi ^ *（x）\ hat {A} \ psi（x）dx$ 。通常，此积分以Dirac表示法编写：

$\ langle \ psi | \帽子{A} | \ psi \ rangle = \ int \极限_ {-\ infty} ^ {+ \ infty} \ psi ^ *（x）\ hat {A} \ psi（x）dx$

一位细心的读者注意到，在薛定ding方程中，已经有一个带盖的装置，

$\帽子{H}$ 。这是系统的能量算子，称为汉密尔顿算子，简称汉密尔顿算子。如前所述，粒子的能量是其动能T和势能V的总和。因此，能源运营商也看起来像：

$\帽子{H} = \帽子{T} + \帽子{V}$

通常，电势只是坐标的函数（

$V = V（x）$ ）及其具体形式取决于任务，但是经典动能看上去像我们已经知道的那样：

$T = \ frac {m v ^ 2} {2} = \ frac {p ^ 2} {2m}$ ，这意味着动能算子看起来像

$\ hat {T} = \ frac {\ hat {p} ^ 2} {2m} =-\ frac {\ hbar ^ 2} {2m} \ frac {d ^ 2} {dx ^ 2}$

。
因此，粒子的薛定ding方程写为

$i \ hbar \ frac {\局部\ psi} {\局部t} = \底线{（\ hat {T} + \ hat {V}）} _ {\ hat {H}} \ psi =-\ frac { \ hbar ^ 2} {2m} \压裂{\部分^ 2 \ psi} {d \部分^ 2} + V（x）\ psi$
这不过是一个二阶偏微分方程，从表面上看，它是一个具有复杂的热扩散系数的热方程。

在很多情况下，我们对系统的稳态问题感兴趣，这时系统没有任何作用，并且在绝对真空和~~必杀技中~~呈球形存在。在这种情况下，包含时间的薛定ding方程被简化，我们只能求解一个更简单的方程：

$\帽子{H} \ psi（x）= E \ psi（x）$

这称为平稳薛定ding方程。它的解决方案是波动函数

$\磅/平方英寸（x）$ 描述稳态和该状态的能量（ E ）。

为了找到电子/介子在质子产生的库仑电场中的运动方式，必须解决量子力学的基本方程式：薛定er方程式。由于所考虑的系统是平稳的（不会随时间变化），因此足以解决其简化形式：平稳的Schrödinger方程，其形式为

$\ underbrace {（\ overbrace {-\ frac {\ hbar ^ 2} {2m} \ cdot \ left（\ frac {\部分^ 2} {\部分x ^ 2} + \ frac {\部分^ 2} { \ partial y ^ 2} + \ frac {\部分^ 2} {\部分z ^ 2} \右）} ^ {\帽子{T}} + \大括号{-\ frac {ke ^ 2} {R}} ^ {\ hat {V}}）} _ {\ hat {H}} \ psi = E \ psi$

这个方程是一个二阶偏微分方程，在其中我们同时搜索波动函数

$\ psi（x，y，z）$ 描述系统的特定状态，并显示质子周围空间中负粒子的“拖尾”现象，以及该状态E的能量。巫术决定它随处可见。

波动函数是什么样的？

$\ psi_ {nlm}（r，\ theta，\ varphi）= \ frac {1} {\ sqrt {2n {\ cdot}（n-l-1）！ {\ cdot}（n + l）！}} {\ cdot} {\左（\ frac {2} {n a_0} \ right）} ^ {\ frac32} {\ cdot} \ exp {\左（{- \ frac {r} {n a_0}} \ right）} {\ cdot} {\左（\ frac {2r} {n a_0} \ right）} ^ {l} L_ {nl-1} ^ {2l + 1 } {\左（\ frac {2r} {n a_0} \右）} \ cdot Y_ {l，m}（\ theta，\ varphi）$

（从Wiki复制）。解以球坐标表示。

但是更简单的事情是：任何熟悉微分方程的人都可以找到类氢原子基态的解决方案。为了不惊吓其他所有人，请在扰流板中将其拆下：

如何找到1s轨道及其能量？

因此，我们在笛卡尔坐标系中有薛定ding方程

$（x，y，z）$ 。但是在氢原子/粒子的情况下更自然

$\ mathrm {p} ^ + \ mu ^-$ 它看起来像球坐标。将质子放在笛卡尔坐标的原点，然后笛卡尔将通过球面表示为

$\ begin {cases} x = R \ cdot \ cos（\ varphi）\ cdot \ sin（\ theta），\\ y = R \ cdot \ sin（\ varphi）\ cdot \ sin（\ theta），\\ z = R \ cdot \ cos（\ theta）\。 \ end {cases}$

在这里R是到质子的距离（与库仑定律相同），并且

$（\ varphi，\ theta）$ 球面角度

$\ varphi$ -平面中的极角

$x0y$ 和

$\ theta$ -粒子从该平面离开的角度：

自然，具有二阶偏导数的块也对应于新坐标：

$\ frac {\部分^ 2 \ psi} {\部分x ^ 2} + \ frac {\部分^ 2 \ psi} {\部分y ^ 2} + \ frac {\部分^ 2 \ psi} {\部分z ^ 2} = \左（\ frac {\部分^ 2 \ psi} {\部分R ^ 2} + \ frac {2} {R} \ frac {\部分\ psi} {\部分R} \右） + \括号{{1 \ R ^ 2 \ sin \ theta} {\部分\ over \部分\ theta} \左（\ sin \ theta \ frac {\部分} {\部分\ theta} \右）\ psi + \ frac {1} {R ^ 2 \ sin ^ 2 \ theta} \ frac {\部分^ 2} {\部分\ varphi ^ 2} \ psi} _ {\文本{如果存在角度依赖性}}$

看来我们的生活变得复杂了，但这并非完全正确。假设波动函数

$\ psi$ 从质子的所有方向都相同（即距中心一定距离，它均匀地分布在该半径的球体上），那么我们的波动函数不取决于角度

$（\ varphi，\ theta）$ ，这意味着很大一部分可怕的二阶导数，它随我们而消失。

结果，剩下一个方程的坐标：

$-\ frac {\ hbar ^ 2} {2m} \ left（\ frac {\部分^ 2 \ psi} {\部分R ^ 2} + \ frac {2} {R} \ frac {\部分\ psi} {\部分R} \对）-\ frac {ke ^ 2} {R} \ psi = E \ psi$

而且，它不再那么令人恐惧，但是，如何求解这样的方程式仍然不是很清楚。

因此，我们将使用肮脏的技巧：在质子紧邻的位置看这个方程（在

$R \ rightarrow 0$ ）在这种情况下，包含2件

$\ frac {1} {R}$ 飙升至巨大的价值，剩下的2名成员死亡，人数仍然很少。

他们不是吃了颠簸吗？

他们无法成长，否则将违反条件

$\ int \极限_ {-\ infty} ^ {+ \ infty} \ int \极限_ {-\ infty} ^ {+ \ infty} \ int \极限_ {-\ infty} ^ {+ \ infty} | \ psi | ^ 2 dx dy dz = 1$ ，肯定可以在某处找到该粒子，因为此积分将变为无穷大，并且将无法修复任何问题。

结果，我们只能为这些大块求解简化的方程式：

$-\ frac {\ hbar ^ 2} {2m} \ frac {2} {R} \ frac {\部分\ psi} {\部分R}-\ frac {ke ^ 2} {R} \ psi = 0$

乘以

$R$ 并在等式的不同方面推这些条件，我们得到标准的一阶差分：

$\ frac {d \ psi} {d R} =-\ frac {mke ^ 2} {\ hbar ^ 2} \ psi$

解决它很简单：

$\ frac {d \ psi} {\ psi} =-\ frac {mke ^ 2} {\ hbar ^ 2} dR \ Rightarrow \ int _ {\ psi_0 = \ psi（R = 0）} ^ {\ psi（R ）} \ frac {d \ psi} {\ psi} =-\ frac {mke ^ 2} {\ hbar ^ 2} \ int_ {0} ^ {R} dR \ Rightarrow \ ln \ left（\ frac {\ psi （R）} {\ psi_0} \ right）=-\ frac {mke ^ 2} {\ hbar ^ 2} R$

换句话说，波动函数具有以下形式：

$\ psi（R）= \ psi_0 \ cdot \ exp \左（-\底线{\ frac {mke ^ 2} {\ hbar ^ 2}} _ {1 / R_1} R \ right）= \ psi_0 \ cdot \ exp \左（-\ frac {R} {R_1} \右）$
在哪里

$\ psi_0$ 这只是某种系数，但是

$R_1 = \ frac {\ hbar ^ 2} {mke ^ 2}$ 玻尔轨道的半径是

$n = 1$ （请参阅上一节）。出乎意料的是，旧的解决方案再次出现在诚实的量子力学中。

仍然需要验证所获得的波函数是否是各地（而不仅仅是质子附近）薛定ding方程的解。为此，我们将结果解替换为原始方程式，为此可以方便地预先找到相对于R的二阶导数：

$\ frac {d ^ 2 \ psi（R）} {dR ^ 2} = \ frac {d} {dR} \底线{\ psi_0 \ exp \左（-\ frac {R} {R_1} \ right）} _ {\ psi（R）} \ cdot \左（-\ frac {1} {R_1} \ right）= \ frac {\ psi（R）} {R_1 ^ 2} = \ frac {m ^ 2k ^ 2e ^ 4} {\ hbar ^ 4} \ cdot \ psi（R）$

替换的结果是：

$\ underbrace {\ frac {mk ^ 2 e ^ 4} {2 \ hbar ^ 2} \ psi（R）} _ {-\ frac {\ hbar ^ 2} {2m} \ frac {\部分^ 2 \ psi （R）} {\部分R ^ 2}} + \底线{（-\ frac {\ hbar ^ 2} {2m} \ frac {2} {R} \ frac {\部分\ psi（R）} {\部分R}-\ frac {ke ^ 2} {R} \ psi（R））} _ {0 \ \文字{（我们已经确定）}} = E \ psi（R）$

即

$\ frac {m k ^ 2 e ^ 4} {2 \ hbar ^ 2} \ psi（R）= E \ psi（R）$ ，解决方案仍然是解决方案。和切割

$\磅/平方英寸（R）$ 在左侧和右侧，我们得到：

$E =-\ frac {m k ^ 2 e ^ 4} {2 \ hbar ^ 2}$ ，等于玻尔轨道的能量

$n = 1$ 。

薛定ding方程的求解结果是一组轨道，使用三个整数n ， l和m （称为“量子数”）对其进行描述。这些轨道的能量依赖于

$（n，l，m）$ 如下所示（以及来自化学领域的冷门知识）：

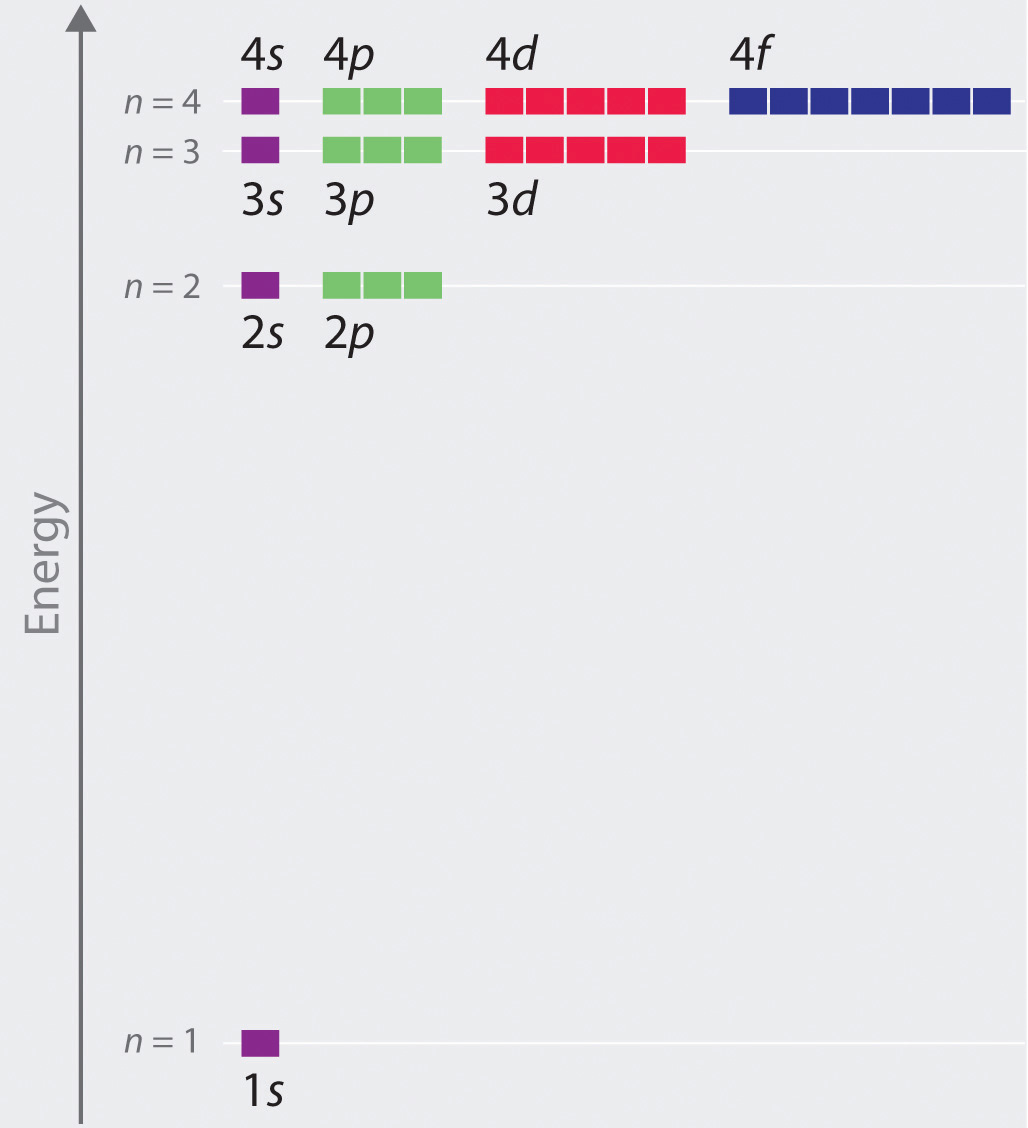
第一个数字n = 1,2,3，...我们已经见过面。这就是所谓的主量子数。它确定了水平面的能量以及玻尔轨道的大小。 (.. ) «». , / , , — , , , . n =1 n =2 ( ):

: , n . , .
l , , . n , n ( l=0,1,2,…,n ). , . , , . , ( ψ=0 ), , . - ( ):

«» . , .
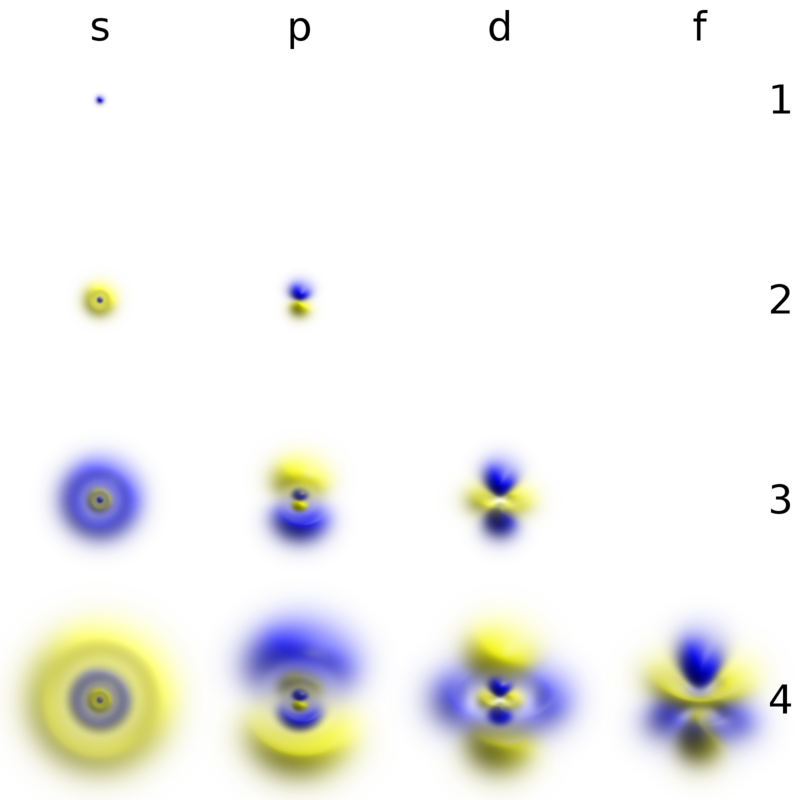
- $l=0$ , , , . s-.
- ( $l=1$ ) p-.
- 4- $l=2$ , d-. .
- 6- ( $l=3$ ) f-.
- 8- ( $l=4$ ) g-.
- 10- ( $l=5$ ) h-.
- .. 等
, ( n ) , . : , .
, m , . . 2l+1 : 。 $m = -l, -l+1, \ldots, 0 , \ldots , l-1, l$

结果是：量子情况下的能量被证明与玻尔相同，但给定n的可能状态数也变成了有限数。而且这个数字随着轨道能量的增加而增长。出乎意料，但与实验非常吻合。

那么氢原子（）从其介子类似物（ $\mathrm{H}^\cdot = \mathrm{p^+ e^-}$ ）？ $\mathrm{p}^+ \mu^-$

现在，我们应用获得的公式，以了解当电子被氢原子中的介子取代时，究竟发生了什么变化。

基态能量（即能量最小，最稳定，无处可去），主量子数n = 1。由公式给出
$E_1 = - \frac{m k^2 e^4}{2 \underbrace{n^2}_{1^2} \hbar^2} = - \frac{m k^2 e^4}{2 \hbar^2}$

当电子转移到μ子时，只有质量（ $m_{\mu} \approx 207 m_\mathrm{e}$ , — , — ). , 207 : $E_1(\mathrm{p}^+\mu^-) = 207 E_1(\mathrm{H}^\cdot)$
. //, . $\mathrm{A \rightarrow A^+ + e^-}$ , A — . , $\mathrm{A \rightarrow A^+ + \mu^-}$ . . $E=0$ . $E_n = - \frac{m k^2 e^4}{2{n^2}\hbar^2}$ $n \rightarrow + \infty$ . 即 , , / , , - (. ).

, ( $E>0$ , ).

, (IP) +/ :
$\mathrm{IP} = \underbrace{0}_{\text{ }} - \underbrace{E_1}_{\text{ }} = -E_1$

, + 207 , , .. «» , .
, «». , , (1s-)
$\psi_{1s}(R) = c\cdot \exp\left(-\frac{R}{R_1} \right)$

$R_1 = \frac{\overbrace{n^2}^{1^2} \hbar^2 }{mk e^2} = \frac{ \hbar^2 }{mk e^2}$ ，波函数随着与质子距离的增加而减小的越快，其“大小”越小，即带负电的粒子的定位。当从电子传递到质子时，该半径R ₁减小207倍；因此，事实证明，质子比电子更紧密地附着在质子上。因此，将其撕掉更加困难，因为电离本质上是向无限远轨道（即轨道）的过渡。介子需要比电子走更多的距离才能从质子中逸出。

从概念上讲，我们从公式得出的所有结论都是无限简单的：

$\ mathrm {H ^ \ cdot}$ 和

$\ mathrm {p} ^ + \ mu ^-$ 看起来一样，但由于介子较重，它更粘在质子上，因此他更难逃脱。

显然是吧？但是有了公式，它仍然更加明显。

接下来会发生什么？

本文只是下一部分的准备。

在其中，我们将直接讨论所提出的降低最低熔化温度的机制。

PS原子单位制

最后，我们讨论一种可以大大简化上面所有公式的事物。在不同的（甚至是学校）任务中，度量单位的选择可以极大地便利生活。对于量子力学，还有一个非常方便的单位系统。这就是所谓的原子单位制。它属于自然单位的类别，与人类中心单位（ SI ， GHS ）本质上相反，在自然人单位中，人们可以立即想象的数量用作参考件。例如，在SI中，长度的单位是米（大约是成年人的一条胳膊/腿的长度），质量-公斤（大约是慕尼黑啤酒节的一圈啤酒的质量），这是我们在日常生活中观察到的所有信息。

但是，自然单位制将简化相应知识领域中的公式作为基础。对于原子单位：

首先，普适的普朗克常数假定为1（ $\ hbar = 1$ ），
质量单位是电子的质量 $m_ \ mathrm {e} \约9.1 \乘以10 ^ {-31}$ 公斤
电荷单位是质子电荷（或等效地，电子电荷模量） $e = 1.6 \乘以10 ^ {-19}$ l
好吧，同时以电常数为单位 $k = \ frac {1} {4 \ pi \ varepsilon_0}$ ，因此库仑定律采用以下形式 $V（R）= \ frac {q_1 q_2} {R}$ 。

在这种情况下，氢原子基态的玻尔半径成为长度单位

$a_0 = R_1 = \ frac {\ hbar ^ 2} {m_ \ mathrm {e} k e ^ 2} = 1$ （我们记得，这大约是0.5Å）。能量的单位变为一个称为Hartree的值（以纪念Hartree的D 角），该值表示为

$E_ \ mathrm {h} = \ frac {m_ \ mathrm {e} k ^ 2 e ^ 4} {\ hbar ^ 2} = 1$ 。可以看出，以原子为单位的氢的1s能级的能量为0.5 Hartree。

在下一部分中，我们将积极参与这些部门。

有趣的事实

学校化学班的每个人都熟悉原子质量单位（amu）。这些是元素周期表中给出的（主要碳同位素质量的1/12

${} ^ {12} \ mathrm {C}$ ）因此，质量的原子单位不属于原子单位系统！ 1 amu大约等于1800质量的电子（单位原子系统的质量单位）。历史上产生了这种误解：它起源于19世纪的化学界，而20世纪上半叶出现在物理界的单位原子系统。为避免这种混乱，IUPAC将amu重命名为在道尔顿，并且自90年代以来就积极地强行指定这个名称，但不幸的是，它并不是很成功。

在量子化学方面的Muon催化。 第一部分：普通氢气与 介子氢

引言