了解Q学习，“走在岩石上”的问题

哈Ha！ 我提请您注意卢卡斯·巴斯克斯 （ Lucas Vazquez）的文章“理解Q学习，悬崖行走问题”的译文。

在上一篇文章中，我们提出了“在岩石上行走”的问题，并解决了一个没有意义的可怕算法。 这次，我们将揭示此灰色框的秘密，并看到它并不那么可怕。

总结

我们得出的结论是，通过最大化未来奖励的数量，我们还找到了实现目标的最快途径，所以我们现在的目标是找到一种实现此目标的方法！

Q学习简介

• 让我们从建立一个表开始，该表衡量某个动作在任何状态下的执行情况（我们可以用简单的标量值来衡量它，因此值越大，动作越好）
• 该表的每种状态都有一行，而每个动作都有一行。 在我们的世界中，网格具有48个状态（4个Y乘以X 12个X乘），并且允许进行4个操作（上，下，左，右），因此表格将为48 x 4。
• 该表中存储的值称为“ Q值”。
• 这些是对未来奖励金额的估计。 换句话说，他们估计在游戏结束之前，处于状态S和执行动作A之前，我们可以获得多少奖励。
• 我们使用随机值（或某个常数，例如全零）初始化表。

最佳的“ Q表”具有允许我们在每种状态下采取最佳行动的值，从而为我们提供了最终获胜的最佳方法。 问题解决了，干杯，机器人勋爵:)。

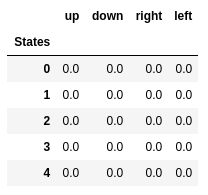前五个状态的Q值。

Q学习

• Q学习是一种“学习”这些值的算法。
• 在每一步中，我们都会获得有关世界的更多信息。
• 此信息用于更新表中的值。

例如，假设我们离目标（平方[2，11]）仅一步之遥，如果我们决定下降，我们将获得0而不是-1的奖励。
我们可以使用此信息来更新表中的状态-动作对的值，下次访问它时，我们已经知道向下移动会给我们0的奖励。

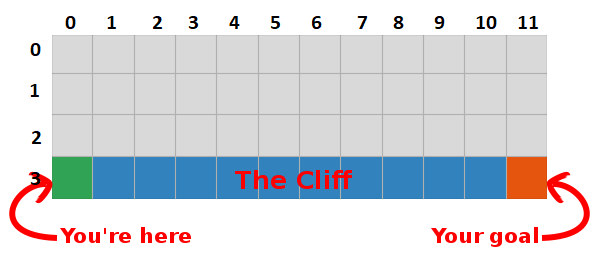
现在，我们可以进一步传播此信息！ 由于我们现在知道从平方[2，11]到目标的路径，任何将我们引向平方[2，11]的动作也将是好的，因此我们更新平方的Q值，从而将我们引向[2，11]接近0。

女士们，先生们，这就是Q学习的精髓！

请注意，每次达到目标时，我们都会将实现目标的“图”增加一个平方，因此，经过足够的迭代，我们将获得完整的图，该图将向我们展示如何从每个状态达到目标。

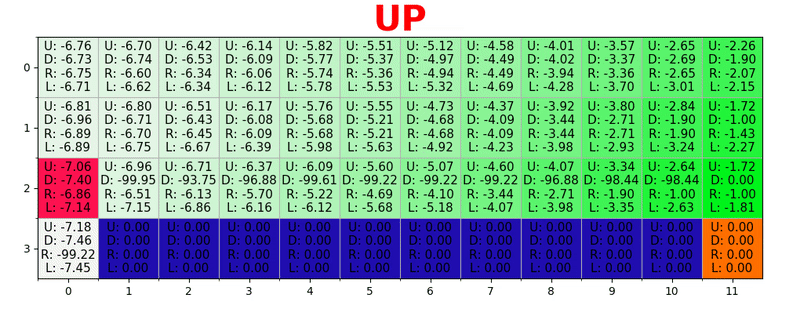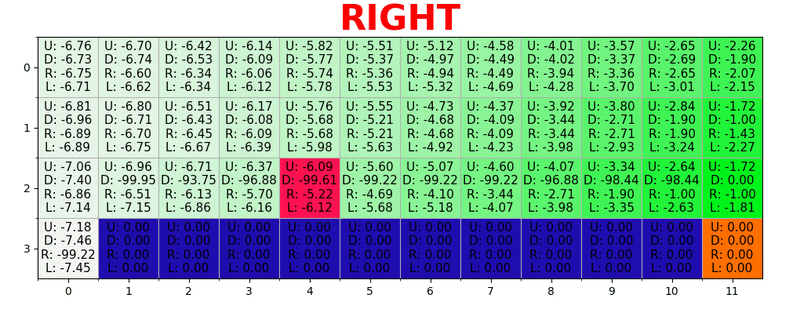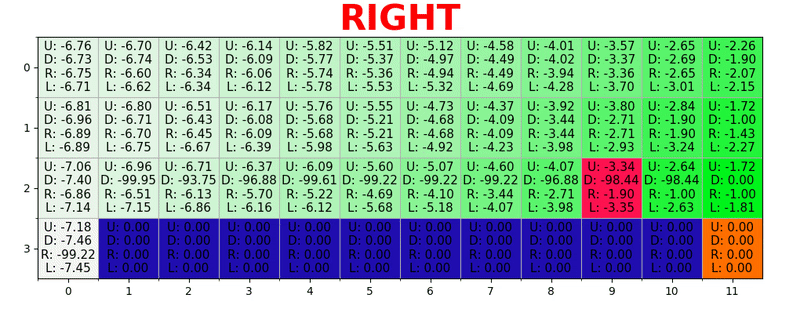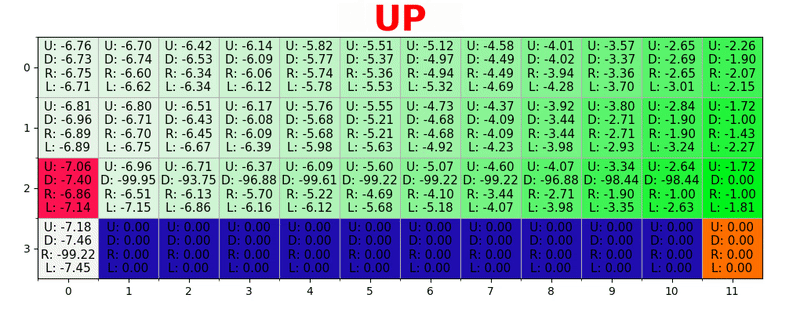通过在每种状态下采取最佳措施来生成路径。 绿色键代表更好操作的含义，更多饱和键代表更高的值。 文本代表每个动作的值（上，下，右，左）。

贝尔曼方程

在讨论代码之前，让我们谈一下数学：Q学习的基本概念，即Bellman方程。

• 首先让我们忘记这个方程中的γ
• 该方程式指出，特定状态-动作对的Q值应该是转换到新状态（通过执行此动作）时收到的奖励，并添加到下一个状态的最佳动作的值中。

换句话说，我们一次只散布有关动作值的信息！

但是我们可以决定，现在获得奖励比将来获得奖励更有价值，因此，我们有一个γ，即0到1（通常是0.9到0.99）的数字与将来的奖励相乘，打折未来的奖励。

因此，给定γ= 0.9并将其应用于世界的某些状态（网格），我们有：

我们可以将这些值与GIF中的上述值进行比较，然后看得出它们是相同的。

实作

既然我们对Q学习的工作方式有了直观的了解，我们就可以开始考虑实现所有这些，并且我们将使用Sutton本书中的Q学习伪代码作为指南。

萨顿书中的伪代码。

代码：

# Initialize Q arbitrarily, in this case a table full of zeros q_values = np.zeros((num_states, num_actions)) # Iterate over 500 episodes for _ in range(500): state = env.reset() done = False # While episode is not over while not done: # Choose action action = egreedy_policy(q_values, state, epsilon=0.1) # Do the action next_state, reward, done = env.step(action) # Update q_values td_target = reward + gamma * np.max(q_values[next_state]) td_error = td_target - q_values[state][action] q_values[state][action] += learning_rate * td_error # Update state state = next_state 

• 首先，我们说：“对于所有状态和动作，我们都可以任意初始化Q（s，a）”，这意味着我们可以使用自己喜欢的任何值创建Q值表，它们可以是随机的，也可以成为任何永久性都没有关系。 我们看到在第2行中，我们创建了一个充满零的表。

我们还说：“最终状态的Q值为零”，我们不能在最终状态中采取任何动作，因此我们认为该状态下所有动作的值为零。

• 对于每一集，我们都必须“初始化S”，这只是说“重新开始游戏”的一种奇特方式，在我们的情况下，这意味着将玩家置于开始位置。 在我们的世界中，有一种方法可以做到这一点，我们在第6行将其称为。
• 对于每个时间步长（每次我们需要采取行动），我们必须选择从Q中获得的行动。

记得，我说过：“我们是否在每种情况下都采取了最有价值的行动？

执行此操作时，我们使用Q值创建策略； 在这种情况下，这将是一个贪婪的政策，因为我们一直认为在每个州都采取最好的行动，因此，我们被称为贪婪地行动。

垃圾

但是这种方法存在一个问题：假设我们处于一个迷宫中，有两个奖励，一个奖励为+1，另一个奖励为+100（每次找到其中一个，游戏都会结束）。 由于我们总是采取我们认为是最好的行动，因此我们将被困在发现的第一个奖项上，并一直返回，因此，如果我们首先承认+1奖项，那么我们将错过+100大奖。

解决方案

我们需要确保已经充分研究了我们的世界（这是一项非常艰巨的任务）。 这就是ε起作用的地方。 贪婪算法中的ε意味着我们必须热心行动，但要随时间做ε百分比的随机动作，因此，在进行无数次尝试后，我们必须检查所有状态。

根据第12行中的此策略选择操作，epsilon = 0.1，这意味着我们有10％的时间在世界上进行研究。 该政策的执行情况如下：

 def egreedy_policy(q_values, state, epsilon=0.1): # Get a random number from a uniform distribution between 0 and 1, # if the number is lower than epsilon choose a random action if np.random.random() < epsilon: return np.random.choice(4) # Else choose the action with the highest value else: return np.argmax(q_values[state]) 

在第一个清单的第14行中，我们调用step方法执行操作，世界将向我们返回下一个状态，奖励和有关游戏结束的信息。

回到数学：

我们有一个长方程，让我们考虑一下：

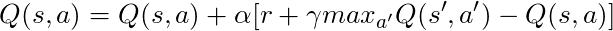
如果我们取α= 1：

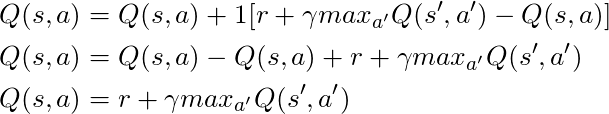
完全符合我们在几段前所看到的Bellman方程！ 因此，我们已经知道这是负责传播有关状态值的信息的行。

但通常α（通常称为学习速度）远小于1，它的主要目标是避免一次更新发生较大变化，因此我们要慢慢接近它，而不是飞向目标。 在我们的表格方法中，设置α= 1不会引起任何问题，但是在使用神经网络时（以下文章中将对此进行详细介绍），所有事情都很容易失控。

查看代码，我们看到在第一个清单的第16行中，我们定义了td_target，这是我们应该更接近的值，但是我们没有直接转到第17行中的该值，而是计算td_error，而是将这个值与速度结合使用学习慢慢地朝目标迈进。

请记住，这个等式是一个Q学习实体。

现在我们只需要更新状态，一切就绪，这就是第20行。我们重复此过程，直到到达情节的结尾，死在岩石中或达到目标为止。

结论

现在，我们直观地了解并知道如何编码Q-Learning（至少是表格形式），请确保检查用于该帖子的所有代码（可在GitHub上找到） 。

可视化学习过程测试：

请注意，所有动作均以超出其最终价值的价值开始，这是刺激探索世界的一种把戏。