最后,出现了朱莉娅语言的俄语指南 。 它为那些缺乏编程经验的人(对该语言的其余部分将对一般开发有用)提供了对该语言的完整介绍,还提供了机器学习的介绍以及一堆整合材料的任务。
在搜索过程中,我遇到了针对经济学家的编程课程(除了朱莉娅,还有Python)。 有经验的可以参加快速课程或阅读《 如何像计算机科学家一样思考》一书
以下是克里斯托弗·拉卡卡斯(Christopher Rackauckas)博客7朱莉娅·格查斯( Julia Gotchas) 和如何处理它们的内容的译文
首先让我说朱莉娅是一门很棒的语言。 我爱她,这是我认为我使用过的最强大,最直观的语言。 无疑,这是我最喜欢的语言。 但是,您需要了解一些“陷阱”,棘手的小事情。 每种语言都有它们,掌握该语言必须要做的第一件事就是找出它们是什么以及如何避免它们。 这篇文章的重点是通过揭示一些建议使用其他编程方法的最常见
朱莉娅(Julia)是一门了解正在发生的事情的好语言,因为它没有魔法。 Julia开发人员希望有明确定义的行为规则。 这意味着可以解释所有行为。 但是,这可能意味着您必须费力地理解为什么会发生这种情况,而不是其他情况正在发生。 这就是为什么我不仅要解释一些常见问题,而且还要解释为什么会出现这些问题。 您将看到有一些非常相似的模式,一旦您意识到它们,您就不会再无所适从了。 因此,与诸如MATLAB / R / Python之类的简单语言相比,Julia的学习曲线要陡峭得多。 但是,一旦掌握了这一点,就可以充分利用Julia的简洁主义来获得C / Fortran性能。 现在深入研究。
出乎意料的是:REPL(终端)具有全球范围
这是迄今为止新的Julia用户报告的最常见问题。 有人会说:“我听说,朱莉娅很快!”,打开REPL,迅速写下一些著名的算法并执行此脚本。 执行完后,他们会看时间说:“等等,为什么它慢,就像在Python中一样?” 由于这是一个重要且常见的问题,因此,让我们花一些时间探索发生这种情况的原因,以找出如何避免这种情况。
题外话:朱莉娅为什么快
您必须了解,Julia不仅是代码的汇编,而且还是类型的特殊化(即,特定于这些类型的代码的汇编)。 让我重申一下:朱莉娅并不快,因为代码是使用JIT编译器编译的,而速度的奥秘在于,可以编译特定于类型的代码。
如果您需要一个完整的故事,请查看我为即将举行的研讨会写的一些笔记。 类型特定性由Julia设计的基本原则确定: 多重调度 。 当您编写代码时:
function f(a,b) return 2a+b end
看来这只是一个f(2.0,3.0) ,Julia将运行编译后的代码,该代码采用两个浮点数并返回2a + b 。 如果调用f(2,3) ,则Julia将运行另一个采用两个整数并返回2a + b编译代码。 函数f是具有相同形式的许多不同方法的抽象或缩写,这种使用符号f调用所有这些不同方法的方案称为多重调度。 这适用于所有地方: +运算符实际上是一个函数,它将根据所看到的类型来调用方法。 Julia真正获得它的速度是因为它编译的代码知道其类型,因此,调用f(2.0,3.0)的编译代码正是您通过在C / Fortran中定义相同的函数而获得的编译代码。 您可以使用code_native宏进行检查,以查看编译后的程序集:
@code_native f(2.0,3.0)
pushq %rbp movq %rsp, %rbp Source line: 2 vaddsd %xmm0, %xmm0, %xmm0 vaddsd %xmm1, %xmm0, %xmm0 popq %rbp retq nop
这是您期望从C / Fortran中的函数使用的同一汇编程序集,并且与整数的汇编代码不同:
@code_native f(2,3) pushq %rbp movq %rsp, %rbp Source line: 2 leaq (%rdx,%rcx,2), %rax popq %rbp retq nopw (%rax,%rax)
实质:REPL / Global Scope不允许类型特异性
这将我们带到要点:REPL /全局范围比较慢,因为它不允许类型指定。 首先,请注意REPL是全局范围,因为Julia允许函数的嵌套范围。 例如,如果我们定义
function outer() a = 5 function inner() return 2a end b = inner() return 3a+b end
我们将看到此代码有效。 这是因为Julia允许您从外部函数捕获到内部函数。 如果递归地应用此思想,您将意识到最高的区域是直接REPL的区域(这是Main模块的全局范围)。 现在让我们考虑一下在这种情况下函数将如何编译。 我们实现相同的事情,但是使用全局变量:
a=2.0; b=3.0 function linearcombo() return 2a+b end ans = linearcombo()
和
a = 2; b = 3 ans2= linearcombo()
问题:编译器应接受a和b哪些类型? 请注意,在此示例中,我们更改了类型并仍然调用相同的函数。 它可以处理我们添加到其中的任何类型:浮点型,整数,数组,奇怪的用户类型等。在Julia中,这意味着必须将变量装箱,并在每次使用它们时检查类型。 您认为编译后的代码是什么样的?
大块 pushq %rbp movq %rsp, %rbp pushq %r15 pushq %r14 pushq %r12 pushq %rsi pushq %rdi pushq %rbx subq $96, %rsp movl $2147565792, %edi # imm = 0x800140E0 movabsq $jl_get_ptls_states, %rax callq *%rax movq %rax, %rsi leaq -72(%rbp), %r14 movq $0, -88(%rbp) vxorps %xmm0, %xmm0, %xmm0 vmovups %xmm0, -72(%rbp) movq $0, -56(%rbp) movq $10, -104(%rbp) movq (%rsi), %rax movq %rax, -96(%rbp) leaq -104(%rbp), %rax movq %rax, (%rsi) Source line: 3 movq pcre2_default_compile_context_8(%rdi), %rax movq %rax, -56(%rbp) movl $2154391480, %eax # imm = 0x806967B8 vmovq %rax, %xmm0 vpslldq $8, %xmm0, %xmm0 # xmm0 = zero,zero,zero,zero,zero,zero,zero,zero,xmm0[0,1,2,3,4,5,6,7] vmovdqu %xmm0, -80(%rbp) movq %rdi, -64(%rbp) movabsq $jl_apply_generic, %r15 movl $3, %edx movq %r14, %rcx callq *%r15 movq %rax, %rbx movq %rbx, -88(%rbp) movabsq $586874896, %r12 # imm = 0x22FB0010 movq (%r12), %rax testq %rax, %rax jne L198 leaq 98096(%rdi), %rcx movabsq $jl_get_binding_or_error, %rax movl $122868360, %edx # imm = 0x752D288 callq *%rax movq %rax, (%r12) L198: movq 8(%rax), %rax testq %rax, %rax je L263 movq %rax, -80(%rbp) addq $5498232, %rdi # imm = 0x53E578 movq %rdi, -72(%rbp) movq %rbx, -64(%rbp) movq %rax, -56(%rbp) movl $3, %edx movq %r14, %rcx callq *%r15 movq -96(%rbp), %rcx movq %rcx, (%rsi) addq $96, %rsp popq %rbx popq %rdi popq %rsi popq %r12 popq %r14 popq %r15 popq %rbp retq L263: movabsq $jl_undefined_var_error, %rax movl $122868360, %ecx # imm = 0x752D288 callq *%rax ud2 nopw (%rax,%rax)
对于没有类型专业化的动态语言,此肿的代码以及所有额外的说明都尽可能地好,因此Julia的速度变慢了。 要了解为什么它如此重要,请注意,您在Julia中编写的每段代码都会编译。 假设您在脚本中编写了一个循环:
a = 1 for i = 1:100 a += a + f(a) end
编译器将不得不编译此循环,但是由于不能保证类型不会更改,因此保守地在所有类型上包裹了一块脚印,这导致执行缓慢。
如何避免问题
有几种方法可以避免此问题。 最简单的方法是始终将脚本包装在函数中。 例如,先前的代码将采用以下形式:
function geta(a) # can also just define a=1 here for i = 1:100 a += a + f(a) end return a end a = geta(1)
这将为您提供相同的结果,但是由于编译器可以专门处理类型a ,因此它将提供所需的已编译代码。 您可以做的另一件事是将变量定义为常量。
const b = 5
通过这样做,您告诉编译器该变量不会更改,因此它将能够将使用该变量的所有代码专门化为当前的类型。 朱莉娅实际上允许您更改常量的值,但不允许更改类型,这有点奇怪。 因此,可以使用const告诉编译器您不会更改类型。 但是,请注意,有一些小问题:
const a = 5 f() = a println(f()) # Prints 5 a = 6 println(f()) # Prints 5 # WARNING: redefining constant a
这不能按预期方式工作,因为编译器意识到他知道f () = a的答案(因为a是一个常数),因此简单地用答案替换了函数调用,与a不是常数时产生了不同的行为。
道德:不要直接在REPL中编写脚本,请始终将它们包装在函数中。
Nezhdanchik第二种:类型不稳定
因此,我只是对代码专业化对数据类型的重要性发表了意见。 我问一个问题,当您的类型可以更改时会发生什么? 如果您猜到:“那么,在这种情况下,您将无法对已编译的代码进行专门化处理,”那么您是对的。 这样的问题被称为类型不稳定性。 它们的外观可能有所不同,但是一个常见的示例是您使用简单的值(但不一定是其应为的类型)来初始化值。 例如,让我们看一下:
function g() x=1 for i = 1:10 x = x/2 end return x end
请注意, 1/2是Julia中的浮点数。 因此,如果我们从x = 1开始,则整数将变为浮点数,因此该函数应编译内部循环,就好像它可以是任何类型一样。 如果相反,我们有:
function h() x=1.0 for i = 1:10 x = x/2 end return x end
那么,如果知道x仍然是浮点数(则编译器确定类型的能力称为类型推断),则整个函数将能够进行最佳编译。 我们可以检查编译后的代码以查看区别:
原生鞋垫 pushq %rbp movq %rsp, %rbp pushq %r15 pushq %r14 pushq %r13 pushq %r12 pushq %rsi pushq %rdi pushq %rbx subq $136, %rsp movl $2147565728, %ebx # imm = 0x800140A0 movabsq $jl_get_ptls_states, %rax callq *%rax movq %rax, -152(%rbp) vxorps %xmm0, %xmm0, %xmm0 vmovups %xmm0, -80(%rbp) movq $0, -64(%rbp) vxorps %ymm0, %ymm0, %ymm0 vmovups %ymm0, -128(%rbp) movq $0, -96(%rbp) movq $18, -144(%rbp) movq (%rax), %rcx movq %rcx, -136(%rbp) leaq -144(%rbp), %rcx movq %rcx, (%rax) movq $0, -88(%rbp) Source line: 4 movq %rbx, -104(%rbp) movl $10, %edi leaq 477872(%rbx), %r13 leaq 10039728(%rbx), %r15 leaq 8958904(%rbx), %r14 leaq 64(%rbx), %r12 leaq 10126032(%rbx), %rax movq %rax, -160(%rbp) nopw (%rax,%rax) L176: movq %rbx, -128(%rbp) movq -8(%rbx), %rax andq $-16, %rax movq %r15, %rcx cmpq %r13, %rax je L272 movq %rbx, -96(%rbp) movq -160(%rbp), %rcx cmpq $2147419568, %rax # imm = 0x7FFF05B0 je L272 movq %rbx, -72(%rbp) movq %r14, -80(%rbp) movq %r12, -64(%rbp) movl $3, %edx leaq -80(%rbp), %rcx movabsq $jl_apply_generic, %rax vzeroupper callq *%rax movq %rax, -88(%rbp) jmp L317 nopw %cs:(%rax,%rax) L272: movq %rcx, -120(%rbp) movq %rbx, -72(%rbp) movq %r14, -80(%rbp) movq %r12, -64(%rbp) movl $3, %r8d leaq -80(%rbp), %rdx movabsq $jl_invoke, %rax vzeroupper callq *%rax movq %rax, -112(%rbp) L317: movq (%rax), %rsi movl $1488, %edx # imm = 0x5D0 movl $16, %r8d movq -152(%rbp), %rcx movabsq $jl_gc_pool_alloc, %rax callq *%rax movq %rax, %rbx movq %r13, -8(%rbx) movq %rsi, (%rbx) movq %rbx, -104(%rbp) Source line: 3 addq $-1, %rdi jne L176 Source line: 6 movq -136(%rbp), %rax movq -152(%rbp), %rcx movq %rax, (%rcx) movq %rbx, %rax addq $136, %rsp popq %rbx popq %rdi popq %rsi popq %r12 popq %r13 popq %r14 popq %r15 popq %rbp retq nop
反对
整齐的汇编符 pushq %rbp movq %rsp, %rbp movabsq $567811336, %rax # imm = 0x21D81D08 Source line: 6 vmovsd (%rax), %xmm0 # xmm0 = mem[0],zero popq %rbp retq nopw %cs:(%rax,%rax)
这样的差异使计算数量获得相同的值!
如何查找和处理类型不稳定

此时,您可能会问:“好吧,为什么不只使用C,这样您就不必寻找这些不稳定性了?” 答案是:
- 容易找到
- 他们可能会有所帮助。
您可以使用功能障碍来处理不稳定问题
Julia提供了code_warntype宏来显示类型不稳定性在哪里。 例如,如果我们在g函数中使用此函数,则会创建:
@code_warntype g()
得到分析 Variables: #self#::#g x::ANY #temp#@_3::Int64 i::Int64 #temp#@_5::Core.MethodInstance #temp#@_6::Float64 Body: begin x::ANY = 1 # line 3: SSAValue(2) = (Base.select_value)((Base.sle_int)(1,10)::Bool,10,(Base.box)(Int64,(Base.sub_int)(1,1)))::Int64 #temp#@_3::Int64 = 1 5: unless (Base.box)(Base.Bool,(Base.not_int)((#temp#@_3::Int64 === (Base.box)(Int64,(Base.add_int)(SSAValue(2),1)))::Bool)) goto 30 SSAValue(3) = #temp#@_3::Int64 SSAValue(4) = (Base.box)(Int64,(Base.add_int)(#temp#@_3::Int64,1)) i::Int64 = SSAValue(3) #temp#@_3::Int64 = SSAValue(4) # line 4: unless (Core.isa)(x::UNION{FLOAT64,INT64},Float64)::ANY goto 15 #temp#@_5::Core.MethodInstance = MethodInstance for /(::Float64, ::Int64) goto 24 15: unless (Core.isa)(x::UNION{FLOAT64,INT64},Int64)::ANY goto 19 #temp#@_5::Core.MethodInstance = MethodInstance for /(::Int64, ::Int64) goto 24 19: goto 21 21: #temp#@_6::Float64 = (x::UNION{FLOAT64,INT64} / 2)::Float64 goto 26 24: #temp#@_6::Float64 = $(Expr(:invoke, :(#temp#@_5), :(Main./), :(x::Union{Float64,Int64}), 2)) 26: x::ANY = #temp#@_6::Float64 28: goto 5 30: # line 6: return x::UNION{FLOAT64,INT64} end::UNION{FLOAT64,INT64}
请注意,在一开始我们说类型x是Any 。 它将使用任何未指定为strict type ,即它是一种抽象类型,需要在每个步骤中将其装箱/选中。 我们看到最后,我们返回x作为UNION {FLOAT64, INT64} ,这是另一个非严格类型。 这告诉我们类型h code_warntype , code_warntype得到所有严格类型:
@code_warntype h() Variables: #self#::#h x::Float64 #temp#::Int64 i::Int64 Body: begin x::Float64 = 1.0 # line 3: SSAValue(2) = (Base.select_value)((Base.sle_int)(1,10)::Bool,10,(Base.box)(Int64,(Base.sub_int)(1,1)))::Int64 #temp#::Int64 = 1 5: unless (Base.box)(Base.Bool,(Base.not_int)((#temp#::Int64 === (Base.box)(Int64,(Base.add_int)(SSAValue(2),1)))::Bool)) goto 15 SSAValue(3) = #temp#::Int64 SSAValue(4) = (Base.box)(Int64,(Base.add_int)(#temp#::Int64,1)) i::Int64 = SSAValue(3) #temp#::Int64 = SSAValue(4) # line 4: x::Float64 = (Base.box)(Base.Float64,(Base.div_float)(x::Float64,(Base.box)(Float64,(Base.sitofp)(Float64,2)))) 13: goto 5 15: # line 6: return x::Float64 end::Float64
这表明该函数是类型稳定的,并且将基本上编译为最佳C代码 。 因此,不难发现类型不稳定性。 更困难的是找到正确的设计。 为什么要解决类型不稳定性? 这是一个长期存在的问题,导致了以下事实:动态类型化的语言在脚本的竞争环境中占主导地位。 这个想法是,在许多情况下,您都希望在性能和可靠性之间找到折衷方案。
例如,您可以从网页中读取表格,其中整数与浮点数混合。 在Julia中,您可以编写函数,以便如果它们都是整数,则可以很好地编译,如果所有都是浮点数,则也可以很好地编译。 如果他们混在一起? 这仍然会起作用。 这是我们从Python / R之类的语言中所了解和喜欢的灵活性/便利性。 但是当您牺牲性能时,Julia会直接( 通过code_warntype )告诉您。
如何处理类型不稳定性
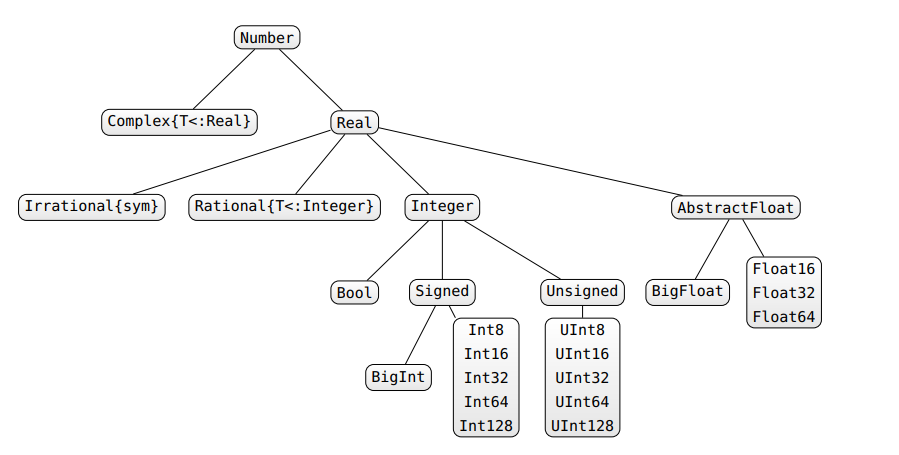
有几种处理类型不稳定性的方法。 首先,如果您喜欢C / Fortran之类的东西,它们声明了您的类型并且不能更改(确保类型稳定性),则可以在Julia中执行以下操作:
local a::Int64 = 5
这将a 64位整数,并且如果以后的代码尝试对其进行更改,则会生成错误消息(或将执行正确的转换。但是由于该转换不会自动舍入,因此很可能会导致错误)。 将它们散布在您的代码周围,即可获得类型稳定性ala, C / Fortran 。 处理此问题的一种较简单的方法是使用类型语句。 在这里,将相同的语法放在等号的另一侧。 例如:
a = (b/c)::Float64
似乎在说:“计算b / c并确保输出为Float64。否则,请尝试执行自动转换。如果无法轻松执行转换,则输出错误。” 放置此类设计将帮助您确保知道涉及的类型。 但是,在某些情况下,类型不稳定是必要的。 例如,假设您想拥有可靠的代码,但用户却给您疯狂的东西,例如:
arr = Vector{Union{Int64,Float64}}(undef, 4) arr[1]=4 arr[2]=2.0 arr[3]=3.2 arr[4]=1
这是一个由4x1整数和浮点数组成的数组。 数组的实际元素类型是Union {Int64, Float64} ,正如我们前面所看到的,它并不严格,这可能会导致问题。 编译器仅知道每个值可以是整数或浮点数,而不能知道哪种类型的元素。 这意味着对这个数组进行算术是幼稚的,例如:
function foo{T,N}(array::Array{T,N}) for i in eachindex(array) val = array[i] # do algorithm X on val end end
由于操作将被装箱,因此速度会很慢。 但是,我们可以使用多个分派以专门的方式运行代码。 这被称为使用功能性障碍。 例如:
function inner_foo{T<:Number}(val::T) # Do algorithm X on val end function foo2{T,N}(array::Array{T,N}) for i in eachindex(array) inner_foo(array[i]) end end
请注意,由于多次分派,调用inner_foo调用专门为浮点数编译的方法或专门为整数编译的方法。 因此,您可以在inner_foo放入很长的计算,并且仍然可以使其正常运行,而不逊于功能障碍为您提供的严格类型。
因此,我希望您看到Julia具有强大的打字性能和动态打字便利性的良好组合。 优秀的程序员Julia可以选择两种方法来最大化生产率和/或必要时的生产率。
惊喜三:Eval在全球范围内运作

朱莉娅最大的优点之一是她的元编程能力。 这使您可以轻松地编写代码生成程序,从而有效地减少了编写和维护所需的代码量。 宏是在编译时运行的函数,(通常)吐出代码。 例如:
macro defa() :(a=5) end
将使用代码a = 5替换任何defa实例( :(a = 5)被引用为expression。Julia的代码为expressions,因此元编程是expressions的集合)。
您可以使用它来构建所需的任何复杂Julia程序,并将其作为一种真正智能的快捷方式放入函数中。 但是,有时您可能需要直接评估生成的代码。 Julia提供了一个eval函数或@eval宏来执行此操作。 通常,您应该尝试避免使用eval ,但是有一些代码是必需的,例如, 我的新库用于在并行编程的不同进程之间传输数据 。 , , :
@eval :(a=5)
(REPL). , / . 例如:
function testeval() @eval :(a=5) return 2a+5 end
, a REPL. , , :
function testeval() @eval :(a=5) b = a::Int64 return 2b+5 end
b — , , , , , . eval , , REPL .
4:
Julia , . : , .
, ? , , . 例如:
a = 2 + 3 + 4 + 5 + 6 + 7 +8 + 9 + 10+ 11+ 12+ 13 a
, 90, 27. ? a = 2 + 3 + 4 + 5 + 6 + 7 , a = 27 , +8 + 9 + 10+ 11+ 12+ 13 , , , :
a = 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10+ 11+ 12+ 13
90, . , .
. — , . rssdev10
. 例如:
x = rand(2,2) a = [cos(2*pi.*x[:,1]).*cos(2*pi.*x[:,2])./(4*pi) -sin(2.*x[:,1]).*sin(2.*x[:,2])./(4)] b = [cos(2*pi.*x[:,1]).*cos(2*pi.*x[:,2])./(4*pi) - sin(2.*x[:,1]).*sin(2.*x[:,2])./(4)]
, a b — , ! (2,2) , — (1-) 2. , , :
a = [1 -2] b = [1 - 2]
: 1 -2 . : 1-2 . - . :
a = [1 2 3 -4 2 -3 1 4]
2x4. , . : hcat :
a = hcat(cos(2*pi.*x[:,1]).*cos(2*pi.*x[:,2])./(4*pi),-sin(2.*x[:,1]).*sin(2.*x[:,2])./(4))
!
№5: ,

(View) — () , ( ), .
, , . , . , .
— "". ""
a = [3;4;5] b = a b[1] = 1
, a — [1; 4; 5] , . . b a . , b = a b a . , , b , , ( b a ). , . , , :
a = rand(2,2) # Makes a random 2x2 matrix b = vec(a) # Makes a view to the 2x2 matrix which is a 1-dimensional array
b , b a , b . , , ( , ). . , . 例如:
c = a[1:2,1]
c a ). , , , , . , , :
d = @view a[1:2,1] e = view(a,1:2,1)
d , e — , d e a , , , reshape , .) , . 例如:
a[1:2,1] = [1;2]
a , a[1:2,1] view (a, 1:2,1) , , a . -? , :
b = copy(a)
, b a , , b a . a , copy! (B, a) , a a ( , b ). . , Vector {Vector} :
a = [ [1, 2, 3], [4, 5], [6, 7, 8, 9] ]
b = copy(a) b[1][1] = 10 a
3-element Array{Array{Int64,1},1}: [10, 2, 3] [4, 5] [6, 7, 8, 9]
, a[1][1] 10! ? copy a . a , b , b . , deepcopy :
b = deepcopy(a)
, . , , .
№6: , In-Place
MATLAB / Python / R . Julia , , , " ".
function f() x = [1;5;6] for i = 1:10 x = x + inner(x) end return x end function inner(x) return 2x end
, inner , , 2x . , . , - y , :
function f() x = [1;5;6] y = Vector{Int64}(3) for i = 1:10 inner(y,x) for i in 1:3 x[i] = x[i] + y[i] end copy!(y,x) end return x end function inner!(y,x) for i=1:3 y[i] = 2*x[i] end nothing end
. inner!(y, x) , y . y , y , , , inner! (y, x) ! ( ).
, inner!(y, x) . copy!(y, x) — , x y , . , , . : x y . , x + inner(x) , , , 11 . , .
, , , . - ( loop-fusion ). Julia v0.5 . ( ( broadcast ), f.(x) — , f x , , . f x , x = x + f. (x) . :
x .= x .+ f.(x)
.= , , ,
for i = 1:length(x) x[i] = x[i] + f(x[i]) end
, :
function f() x = [1;5;6] for i = 1:10 x .= x .+ inner.(x) end return x end function inner(x) return 2x end
MATLAB / R / Python , , , .
: ,
: , . , . , . , , . , .
- , C / Fortran , . - , , !
: ? , . , , ? [ , Javascript var x = 3 x , x = 3 x . ? , - Javascript!]