简介:涉及贝塞尔函数的应用涉及与数学物理学的几乎所有最重要分支有关的大量最多样化的问题,这些问题旨在回答局部技术问题。
贝塞尔函数广泛用于解决声学,放射物理学,流体力学,原子和核物理问题。 贝塞尔函数在热导率理论和弹性理论(板振动问题,壳理论问题,确定裂纹附近应力集中的问题)中有许多应用。
贝塞尔函数之所以如此普及,是因为以下事实:通过经典的变量分离方法,在圆柱坐标系中求解包含拉普拉斯算子的数学物理方程,可以得到一个常微分方程,该方程可用来确定这些函数[1]。
贝塞尔函数以德国天文学家弗里德里希·贝塞尔(Friedrich Bessel)的名字命名,他在1824年研究行星绕太阳运动时,得出了贝塞尔函数的递归关系
Jv(x) 接收整数
v 函数的整体表示
Jv(x) 证明了函数无数零的存在
J0(x) 并编译了第一个函数表
J1(x) 和
J2(x) 。
但是,贝塞尔的功能之一还是第一次
J0(x) 早在1732年,丹尼尔·伯努利(Daniel Bernoulli)就曾致力于重链的振动研究。 D. Bernoulli找到了功能的表达
J0(x) 以幂级数的形式,并注意到(没有证明)方程
J0(x)=0 有无数有效根。
下一个涉及贝塞尔功能的工作是1738年的莱昂纳多·欧拉(Leonardo Euler)的工作,该工作致力于研究圆形膜的振动。 在这项工作中,欧拉(L. Euler)发现了整数
v 贝塞尔函数表达式
Jv(x) 以一系列权力的形式
x ,并在随后的论文中将此表达式扩展到任意索引值的情况
v 。 此外,欧拉(L. Euler)证明了
v 等于整数一半,函数
Jv(x) 通过基本功能表示。
他指出(没有证据)
v 功能
Jv(x) 有无数个实零并且给出了一个整数表示
Jv(x) 。 一些研究人员认为,与贝塞尔函数及其在数学物理学中的应用有关的主要结果与L. Euler的名字有关。
要研究Bessel函数的性质,同时掌握求解简化为Bessel函数的方程式的方法,可以使用自由分发的符号数学程序SymPy-Python库。
在SymPy符号数学程序中,可以使用一系列和的关系来构造第一类整数阶的Bessel函数图:
Jp(x)= sum inftym=0 fracx2m+p(−1)m22m+pm!\伽玛(p+m+1)
第一种贝塞尔函数from sympy import* from sympy.plotting import plot x,n, p=var('x,n, p') def besselj(p,x): return summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]) st="J_{p}(x)" p1=plot(besselj(0,x),(x,-20,20),line_color='b',title=' $'+st+ '$',show=False) p2=plot(besselj(1,x),(x,-20,20),line_color='g',show=False) p3=plot(besselj(2,x),(x,-20,20),line_color='r',show=False) p4=plot(besselj(3,x),(x,-20,20),line_color='c',show=False) p1.extend(p2) p1.extend(p3) p1.extend(p4) p1.show()
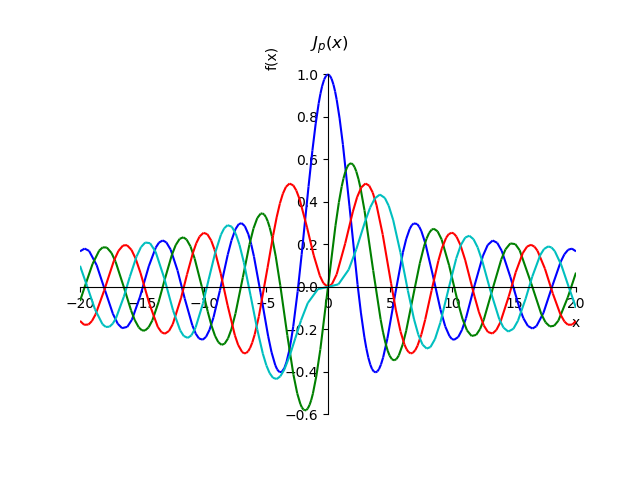
使用该关系求一个序列的和,我们可以证明整个订单的这些函数的性质
J1(x)=−J−1(x):
第一种贝塞尔函数的性质 from sympy import* from sympy.plotting import plot x,n, p=var('x,n, p') def besselj(p,x): return summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]) st="J_{1}(x)=-J_{-1}(x)" p1=plot(besselj(1,x),(x,-10,10),line_color='b',title=' $'+st+ '$',show=False) p2=plot(besselj(-1,x),(x,-10,10),line_color='r',show=False) p1.extend(p2) p1.show()

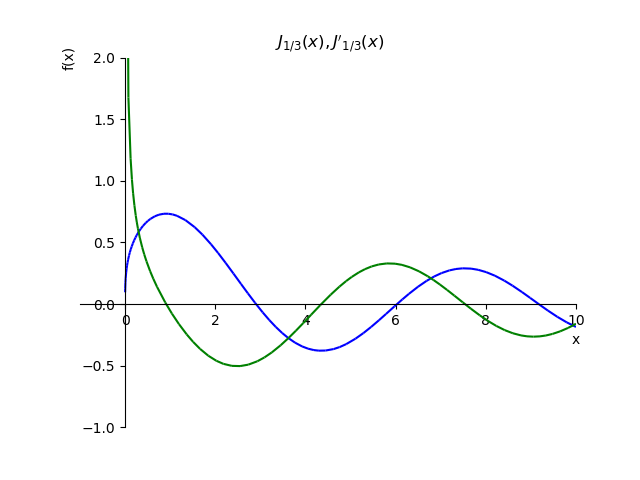
为了演示柯西条件,我们构造了一个函数
J1/3(x) 及其衍生物
fracdJ1/3(x)dx: :
分数阶函数及其导数 from sympy import* from sympy.plotting import plot x,n, p=var('x,n, p') def besselj(p,x): return summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]) st="J_{1/3}(x),J{}'_{1/3}(x)" p1=plot(besselj(1/3,x),(x,-1,10),line_color='b',title=' $'+st+ '$',ylim=(-1,2),show=False) def dbesselj(p,x): return diff(summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]),x) p2=plot(dbesselj(1/3,x),(x,-1,10),line_color='g',show=False) p1.extend(p2) p1.show()
但是,对于实际计算,使用了精彩的mpmath模块,该模块不仅可以数值求解具有第一类和第二类Bessel函数的方程,包括所有容许阶数的经修改的方程,还可以构造具有自动缩放比例的图。
此外,mpmath模块不需要共享符号和数字数学的专用工具。 我已经在出版物[2]中考虑了创建该模块的历史以及将其用于拉普拉斯逆变换的可能性。 现在,我们继续讨论使用Bessel函数的mpmath [3]。
第一种贝塞尔函数 JN(x)mpmath.besselj(n,x,导数= 0) -给出第一类贝塞尔函数
Jn(x) 。 功能介绍
JN(x) 是以下微分方程的解决方案:
x2y′+xy′+(x2−n2)y=0
对于整个积极
n 表现为正弦或余弦,乘以一个系数,该系数随着
x rightarrow pm infty第一种贝塞尔函数
JN(x) 是超几何函数的特例
oF1 :
Jn(x)= fracxn2n Gamma(n+1)oF1(n+1, fracx24)
贝塞尔函数可以区分
m 假设第m个导数不等于零的时间:
fracdmdxmJn(x)
第一种贝塞尔函数
JN(x) 对于正整数阶数n = 0、1、2、3-贝塞尔方程的解:
from mpmath import* j0 = lambda x: besselj(0,x) j1 = lambda x: besselj(1,x) j2 = lambda x: besselj(2,x) j3 = lambda x: besselj(3,x) plot([j0,j1,j2,j3],[0,14]

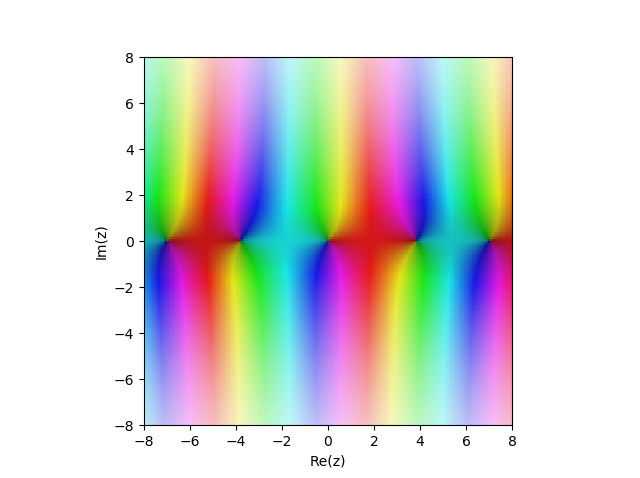
第一种贝塞尔函数
JN(x) 在复杂平面中:
from sympy import* from mpmath import* cplot(lambda z: besselj(1,z), [-8,8], [-8,8], points=50000)
范例:
功能介绍
besselj(N,x) 提供具有给定位数的结果
(mp.dps) 逗号后:
from mpmath import* mp.dps = 15; mp.pretty = True print(besselj(2, 1000)) nprint(besselj(4, 0.75)) nprint(besselj(2, 1000j)) mp.dps = 25 nprint( besselj(0.75j, 3+4j)) mp.dps = 50 nprint( besselj(1, pi))
函数参数可以是大量的:
from mpmath import* mp.dps = 25 nprint( besselj(0, 10000)) nprint(besselj(0, 10**10)) nprint(besselj(2, 10**100)) nprint( besselj(2, 10**5*j))
第一种贝塞尔函数满足关于以下项的简单对称性
x=0 :
from sympy import* from mpmath import* mp.dps = 15 nprint([besselj(n,0) for n in range(5)]) nprint([besselj(n,pi) for n in range(5)]) nprint([besselj(n,-pi) for n in range(5)])
根不是周期性的,而是连续的根之间的距离渐近地接近
2π 。 第一种贝塞尔函数具有以下代码:
from mpmath import* print(quadosc(j0, [0, inf], period=2*pi)) print(quadosc(j1, [0, inf], period=2*pi))
对于
n=1/2 或
n=−1/2 贝塞尔函数简化为三角函数:
from sympy import* from mpmath import* x = 10 print(besselj(0.5, x)) print(sqrt(2/(pi*x))*sin(x)) print(besselj(-0.5, x)) print(sqrt(2/(pi*x))*cos(x))
可以计算任何阶的导数,
负阶对应于积分 :
from mpmath import* mp.dps = 25 print(besselj(0, 7.5, 1)) print(diff(lambda x: besselj(0,x), 7.5)) print(besselj(0, 7.5, 10)) print(diff(lambda x: besselj(0,x), 7.5, 10)) print(besselj(0,7.5,-1) - besselj(0,3.5,-1)) print(quad(j0, [3.5, 7.5]))
具有非整数阶的微分在Riemann-Liouville微分积分的意义上
给出了分数导数 ,使用函数计算
difint() :
from mpmath import* mp.dps = 15 print(besselj(1, 3.5, 0.75)) print(differint(lambda x: besselj(1, x), 3.5, 0.75))
调用第一类零和一阶的Bessel函数的其他方式
mpmath.j0(x) -计算贝塞尔函数
J0(x) ;
mpmath.j1(x) -计算贝塞尔函数
J1(x) ;
第二类贝塞尔函数bessely(n,x,导数= 0)从以下关系式计算第二类贝塞尔函数:
Yn(x)= fracJn(x)cos( pi cdotn)−J−n(x)sin( pi cdotn)
对于整数
n 以下公式应理解为极限。 贝塞尔函数可以区分
m 假设第m个导数不等于零的时间:
fracdmdxmYn(x)第二类贝塞尔函数
Yn(x) 对于整数正订单
n=0,1,2,3 。
from sympy import* from mpmath import* y0 = lambda x: bessely(0,x) y1 = lambda x: bessely(1,x) y2 = lambda x: bessely(2,x) y3 = lambda x: bessely(3,x) plot([y0,y1,y2,y3],[0,10],[-4,1])
第二类贝塞尔函数
Yn(x) 在复杂的飞机上
from sympy import* from mpmath import* cplot(lambda z: bessely(1,z), [-8,8], [-8,8], points=50000)
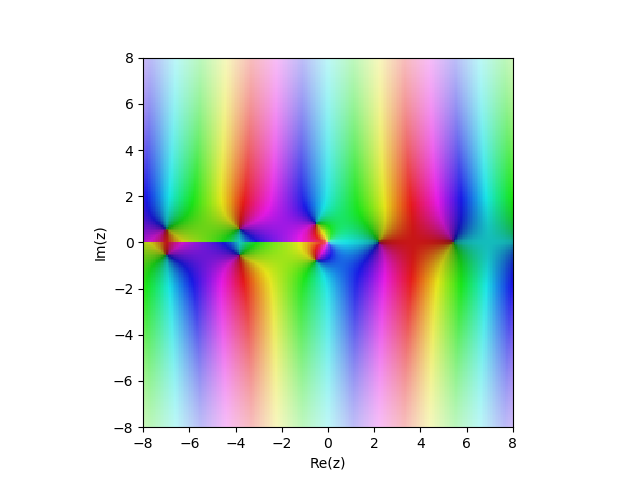
范例:
一些功能值
Yn(x) :
from sympy import* from mpmath import* mp.dps = 25; mp.pretty = True print(bessely(0,0)) print(bessely(1,0)) print(bessely(2,0)) print(bessely(1, pi)) print(bessely(0.5, 3+4j))
参数可能很大:
from sympy import* from mpmath import* mp.dps = 25; mp.pretty = True print(bessely(0, 10000)) print(bessely(2.5, 10**50)) print(bessely(2.5, -10**50))
可以计算任何阶数的导数,包括负数:
from sympy import* from mpmath import* mp.dps = 25; mp.pretty = True print(bessely(2, 3.5, 1)) print(diff(lambda x: bessely(2, x), 3.5)) print(bessely(0.5, 3.5, 1)) print(diff(lambda x: bessely(0.5, x), 3.5)) print(diff(lambda x: bessely(2, x), 0.5, 10)) print(bessely(2, 0.5, 10)) print(bessely(2, 100.5, 100)) print(quad(lambda x: bessely(2,x), [1,3])) print(bessely(2,3,-1) - bessely(2,1,-1))
修改的第一类贝塞尔函数
mpmath.besseli(n, x, derivative=0)
besseli(n,x,导数= 0)修改的第一类Bessel函数
In(x)=\数学i−nJn(ix)
fracdmdxmIn(x)
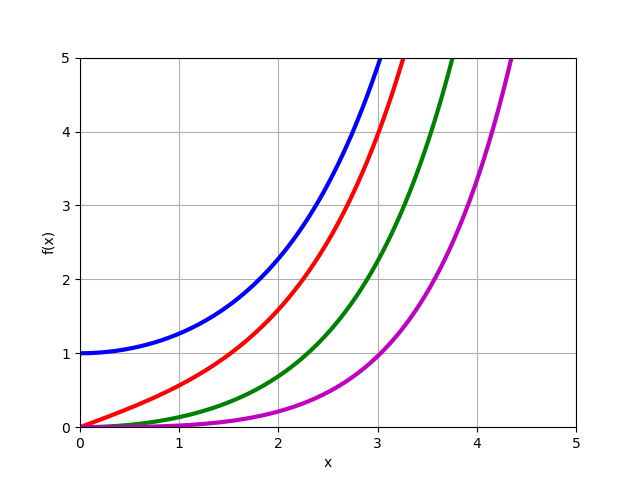
修改的贝塞尔函数
In(x) 对于真实订单
n=0,1,2,3 :
from mpmath import* i0 = lambda x: besseli(0,x) i1 = lambda x: besseli(1,x) i2 = lambda x: besseli(2,x) i3 = lambda x: besseli(3,x) plot([i0,i1,i2,i3],[0,5],[0,5])
修改的贝塞尔函数
In(x) 在复杂的飞机上
from mpmath import* cplot(lambda z: besseli(1,z), [-8,8], [-8,8], points=50000)

范例:
一些意思
In(x) from mpmath import* mp.dps = 25; mp.pretty = True print(besseli(0,0)) print(besseli(1,0)) print(besseli(0,1)) print(besseli(3.5, 2+3j))
参数可能很大:
from mpmath import* mp.dps = 25; mp.pretty = True print(besseli(2, 1000)) print(besseli(2, 10**10)) print(besseli(2, 6000+10000j))
对于整数n,以下整数表示成立:
from mpmath import* mp.dps = 15; mp.pretty = True n = 3 x = 2.3 print(quad(lambda t: exp(x*cos(t))*cos(n*t), [0,pi])/pi) print(besseli(n,x))
可以计算任何阶数的导数:
from mpmath import* mp.dps = 25; mp.pretty = True print(besseli(2, 7.5, 1)) print(diff(lambda x: besseli(2,x), 7.5)) print(besseli(2, 7.5, 10)) print(diff(lambda x: besseli(2,x), 7.5, 10)) print(besseli(2,7.5,-1) - besseli(2,3.5,-1)) print(quad(lambda x: besseli(2,x), [3.5, 7.5]))
第二种修改的贝塞尔函数,
mpmath.besselk(n, x)
besselk(n,x)修改的第二类Bessel函数
Kn(x)= frac pi4 fracI−n(x)−In(x)sin( pi cdotn)
对于整数
n 该公式应理解为极限。
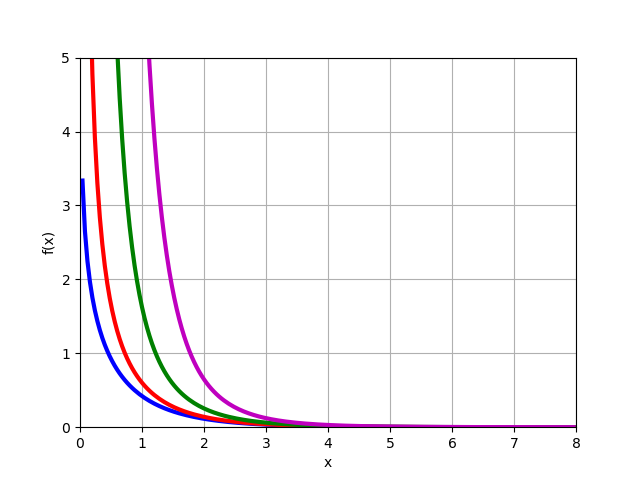
修改后的第二类贝塞尔函数
Kn(x) 用于材料
n=0,1,2,3 :
from mpmath import* k0 = lambda x: besselk(0,x) k1 = lambda x: besselk(1,x) k2 = lambda x: besselk(2,x) k3 = lambda x: besselk(3,x) plot([k0,k1,k2,k3],[0,8],[0,5])
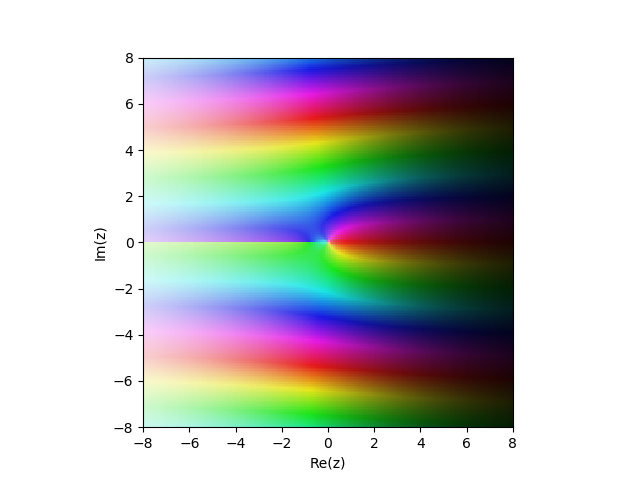
修改后的第二类贝塞尔函数
Kn(x)) 在复杂的飞机上
from mpmath import* cplot(lambda z: besselk(1,z), [-8,8], [-8,8], points=50000)
范例:
复杂的参数:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselk(0,1)) print(besselk(0, -1)) print(besselk(3.5, 2+3j)) print(besselk(2+3j, 0.5))
争论很重要
from mpmath import * mp.dps = 25; mp.pretty = True print(besselk(0, 100)) print(besselk(1, 10**6)) print(besselk(1, 10**6*j)) print(besselk(4.5, fmul(10**50, j, exact=True)))
功能在某点的行为特征
x=0 :
from mpmath import * print(besselk(0,0)) print(besselk(1,0)) for n in range(-4, 5): print(besselk(n, '1e-1000'))
贝塞尔函数零点 besseljzero() mpmath.besseljzero(v, m, derivative=0)
对于真实订单
mathit nu geq0 和一个正整数
m 退货
j nu,m ,第一种Bessel函数的第m个正零
J nu(z) (请参阅
besselj() )。 或者,用
微分=1 给出第一个非负质数零
j′ nu,m 来自
J′ nu(z) 。 使用Abramowitz&Stegun和DLMF的索引协议名称。 注意特殊情况。
j′0,1=0 而其他所有零均为正。
实际上,仅计算简单零(贝塞尔函数的所有零都是简单的,除非
z=0 ),以及
j nu,m 成为的单调函数
nu 和
m 。 零根据不等式交替出现:
j′ nu,k<j nu,k<j′ nu,k+1
j nu,1<j nu+1,2<j nu,2<j nu+1,2<j nu,3 cdots
范例:
贝塞尔函数的前导零
J0(z) ,
J1(z) ,
J2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0,1)) print(besseljzero(0,2)) print(besseljzero(0,3)) print(besseljzero(1,1)) print(besseljzero(1,2)) print(besseljzero(1,3)) print(besseljzero(2,1)) print(besseljzero(2,2)) print(besseljzero(2,3))
贝塞尔函数的导数的前导零
J′0(z) ,
J′1(z) ,
J′2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0,1,1)) print(besseljzero(0,2,1)) print(besseljzero(0,3,1)) print(besseljzero(1,1,1)) print(besseljzero(1,2,1)) print(besseljzero(1,3,1)) print(besseljzero(2,1,1)) print(besseljzero(2,2,1)) print(besseljzero(2,3,1))
具有大索引的零:
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0,100)) print(besseljzero(0,1000)) print(besseljzero(0,10000)) print(besseljzero(5,100)) print(besseljzero(5,1000)) print(besseljzero(5,10000)) print(besseljzero(0,100,1)) print(besseljzero(0,1000,1)) print(besseljzero(0,10000,1))
具有大阶函数的零:
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(50,1)) print(besseljzero(50,2)) print(besseljzero(50,100)) print(besseljzero(50,1,1)) print(besseljzero(50,2,1)) print(besseljzero(50,100,1))
零阶函数零:
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0.5,1)) print(besseljzero(1.5,1)) print(besseljzero(2.25,4))
和
J nu(z) 。 和
J′ nu(z) 可以表示为零的无穷乘积:
from mpmath import * mp.dps = 6; mp.pretty = True v,z = 2, mpf(1) nprint((z/2)**v/gamma(v+1) * \ nprod(lambda k: 1-(z/besseljzero(v,k))**2, [1,inf])) print(besselj(v,z)) nprint((z/2)**(v-1)/2/gamma(v) * \ nprod(lambda k: 1-(z/besseljzero(v,k,1))**2, [1,inf])) print(besselj(v,z,1))
besselyzero() mpmath.besselyzero(v, m, derivative=0)
对于真实订单
mathit nu geq0 和一个正整数
m 退货
y nu,m ,
m ,第二种Bessel函数的第m个正零
Y nu(z) (请参阅
Bessely() )。 或者,用
微分=1 给出第一个正零
y′ nu,m 来自
Y′ nu(z) 。 零根据不等式交替出现:
y nu,k<y′ nu,k<y nu,k+1
y nu,1<y nu+1,2<y nu,2<y nu+1,2<y nu,3 cdots
范例:
贝塞尔函数的前导零
Y0(z) ,
Y1(z) ,
Y2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0,1)) print(besselyzero(0,2)) print(besselyzero(0,3)) print(besselyzero(1,1)) print(besselyzero(1,2)) print(besselyzero(1,3)) print(besselyzero(2,1)) print(besselyzero(2,2)) print(besselyzero(2,3))
贝塞尔函数的导数的前导零
Y′0(z) ,
Y′1(z) ,
Y′2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0,1,1)) print(besselyzero(0,2,1)) print(besselyzero(0,3,1)) print(besselyzero(1,1,1)) print(besselyzero(1,2,1)) print(besselyzero(1,3,1)) print(besselyzero(2,1,1)) print(besselyzero(2,2,1)) print(besselyzero(2,3,1))
具有大索引的零:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0,100)) print(besselyzero(0,1000)) print(besselyzero(0,10000)) print(besselyzero(5,100)) print(besselyzero(5,1000)) print(besselyzero(5,10000)) print(besselyzero(0,100,1)) print(besselyzero(0,1000,1)) print(besselyzero(0,10000,1))
具有大阶函数的零:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(50,1)) print(besselyzero(50,2)) print(besselyzero(50,100)) print(besselyzero(50,1,1)) print(besselyzero(50,2,1)) print(besselyzero(50,100,1))
零阶函数零:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0.5,1)) print(besselyzero(1.5,1)) print(besselyzero(2.25,4))
贝塞尔函数应用贝塞尔函数的重要性不仅在于贝塞尔方程在应用中的频繁出现,还在于许多其他二阶线性微分方程的解可以用贝塞尔函数表示的事实。 为了查看它们的外观,我们从贝塞尔数阶方程开始
p 形式为:
z2 fracd2wdz2+z fracdwdz+(z2−p2)w=0,(1)
并在这里替代
w=x− alpha,z=kx beta,(2)
然后,使用(2)并引入常量
A,B,C 从等式(1),我们得到:
x2y′+轴y′+(B+Cxq)y=0,(3)
A=1−2 alpha,B= alpha2− beta2p2,C= beta2k2,q=2 beta,(4)美
从等式(4)我们得到:
\左\ {\开始{矩阵} \ alpha = \ frac {1-A} {2},\\ \ beta = \ frac {q} {2},\\ k = \ frac {2 \ sqrt {C }} {q} \\ p = \分数{\ sqrt {(1-A ^ {2} -4B}} {q} \\ \ end {matrix} \ right。(5)
如果
C>0 ,
q neq0 ,
(1−A)2 geqslant4B ,然后是一般解决方案(
x>0 方程(3)的形式为:
y(x)=x alpha\左[c1Jp(kx beta)+c2J−p(kx beta)\右](6)
其中:
alpha ,
beta ,
k 由系统(5)确定。 如果
p 然后是整数
Jp 需要替换为
Yp 。
立柱的纵向弯曲现在,我们将考虑一项对于实际应用很重要的任务。 在此任务中,需要确定均匀的垂直柱何时在其自重作用下弯曲。 我们假设
x=0 在该列的自由上端和
x=L>0 在其基础上; 我们假设基座牢固地插入(即固定不动)到基座(插入地面),也可能插入混凝土。
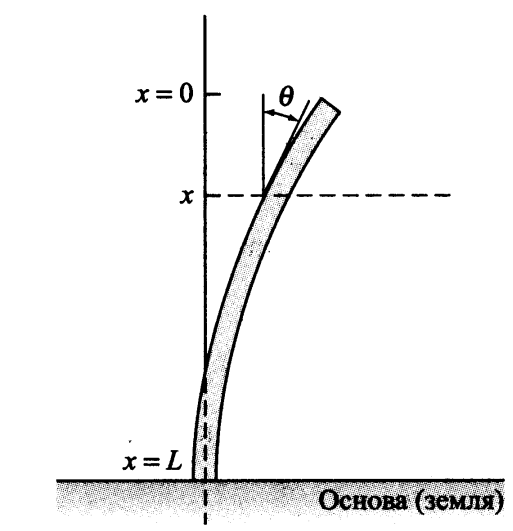
表示柱在该点的角度偏差
x 通过
theta(x) 。 从这些条件下的弹性理论可以得出:
EI fracd2 thetadx2+g rhox theta=0,(7)
在哪里
E -柱材料的杨氏模量,
我 -横截面的惯性矩,
rho -柱的线密度和
g -重力加速度。 边界条件的形式为:
theta′(0)=0, theta(L)=0,(8)
我们将使用(7)和(8)解决问题:
lambda= gamma2= fracg rhoEI(9)
我们在条件(8)下考虑(9)重写(7):
fracd2 thetadx2+ gamma2x theta=0; fracd thetadx=0, theta(L)=0。(10)
仅当对问题有非平凡的解决方案时,柱才能变形(10); 否则,列将保持在不偏离垂直线的位置(即物理上无法偏离垂直线)。
微分方程(10)是艾里方程。 公式(10)具有公式(3)的形式
A=B=0 ,
C= gamma2 ,
q=3 。 从方程式(5)中,我们得到
alpha= frac12 ,
beta= frac32 ,
k= frac23 gamma ,
p= frac13 。
因此,一般解决方案具有以下形式:
theta(x)=x1/2\左[c1J1/3( frac23 gammax3/2)+c2J−1/3( frac23 gammax3/2) right]。(11)
为了应用初始条件,我们用
p= pm frac13 在
Jp= sum inftym=0 frac(−1)mm! Gamma(p+m+1)\左( fracx2 right)2m+p(12)
经过转换(12),考虑到解(11),我们获得:
theta(x)= fracc1 gamma1/331/3 Gamma(4/3)\左(x− frac gamma2x412+ frac gamma4x7504− cdot cdot cdot right)++ fracc231/3 gamma1/3 Gamma( frac23)\左(1− frac gamma2x36+ frac gamma4x6180− cdot cdot cdot right)。(13)
在起点提供
theta′(0)=0 我们得到
c1=0 ,则(11)的形式为:
theta(x)=c2x1/2J−1/3( frac23 gammax3/2),(14)
在终点提供
theta(L)=0 ,从(14)得到:
J−1/3( frac23 gammaL3/2)=0(15)
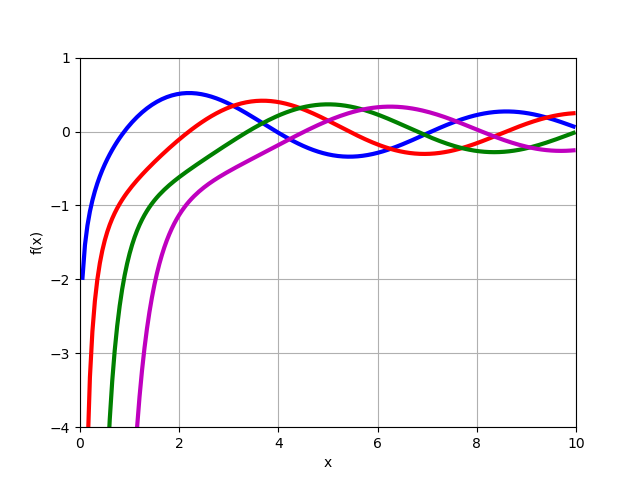
应该注意的是,如果构造函数图,则无法进行变换(13),(14)
J1/3(x),J−1/3(x) 使用mpmath模块的功能:
from mpmath import* mp.dps = 6; mp.pretty = True f=lambda x: besselj(-1/3,x) f1=lambda x: besselj(1/3,x) plot([f,f1], [0, 15])
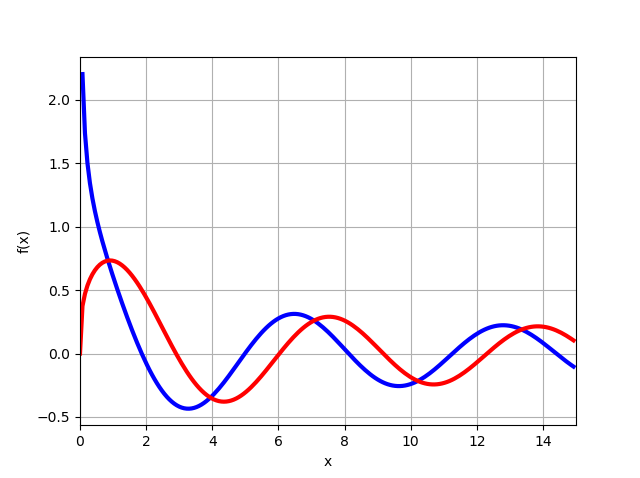
从图中可以看出,对于x = 0,函数
J1/3(0)=0 并考虑到解(11),我们立即获得必要的方程式(15),仅需找到z即可,如下所示。
因此,只有在以下情况下,柱才会变形
z= frac23 gammaL3/2 是等式的根
J−1/3(z)=0 。 建立功能
J−1/3(z) 在单独的图表上:
from mpmath import* mp.dps = 6; mp.pretty = True f=lambda x: besselj(-1/3,x) plot(f, [0, 15])

该图显示第一个根小于2。找到根
z0 从等式
J−1/3(z)=0 您可以使用
findroot(f,z0)函数根据图形接受搜索点
x0=1 和小数点后
六位mp.dps = 6 :
from mpmath import* mp.dps = 6; mp.pretty = True f=lambda x: besselj(-1/3,x) print("z0=%s"%findroot(f, 1)
我们得到:
z0=1.86635我们使用公式(15)计算临界长度,例如旗杆:
部分中不同参数的旗杆高度 from numpy import* def LRr(R,r): E=2.9*10**11
我们得到:
8.47 m
10.25 m
中空的旗杆可能高于实心的旗杆。
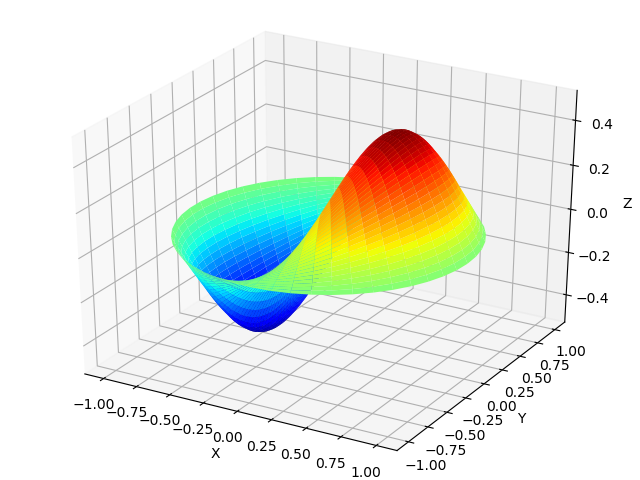
波在薄膜中的传播。
声波进入时,薄膜不仅会随着波的频率而振荡。 可以使用下面的公式
besselj()和
besseljzero()根据以下清单在Bessel函数中获得膜振动的形式:
膜波形 from mpmath import* from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm def Membrana(r): mp.dps=25 return cos(0.5) * cos( theta) *float(besselj(1,r*besseljzero(1,1) ,0)) theta =linspace(0,2*pi,50) radius = linspace(0,1,50) x = array([r * cos(theta) for r in radius]) y = array([r * sin(theta) for r in radius]) z = array([Membrana(r) for r in radius]) fig = plt.figure("") ax = Axes3D(fig) ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel('X') ax.set_ylabel('Y') ax.set_zlabel('Z') plt.show()
SciPy库的特殊Bessel功能中的mpmath模块的替代品
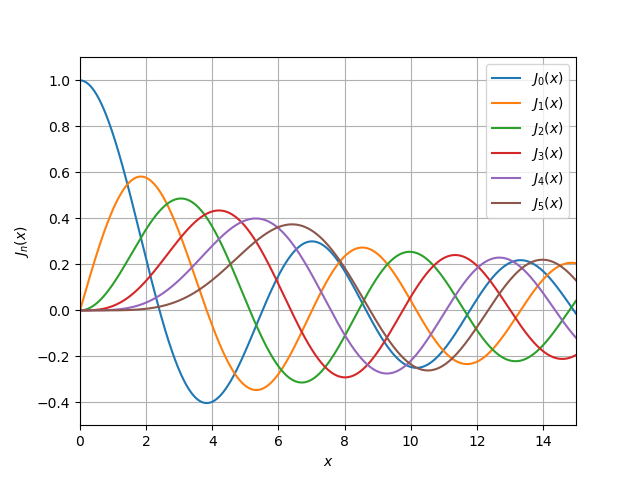
在不深入研究SciPy库[4]中的Bessel函数的情况下,我仅给出两个列表来绘制第一种和第二种
jv(v,x) ,
yv(v,x)的函数 :
jv(v,x) import numpy as np import pylab as py import scipy.special as sp x = np.linspace(0, 15, 500000) for v in range(0, 6): py.plot(x, sp.jv(v, x)) py.xlim((0, 15)) py.ylim((-0.5, 1.1)) py.legend(('$J_{0}(x)$', '$ J_{1}(x)$', '$J_{2}(x)$', '$J_{3}(x)$', '$ J_{4}(x)$','$ J_{5}(x)$'), loc = 0) py.xlabel('$x$') py.ylabel('${J}_n(x)$') py.grid(True) py.show()
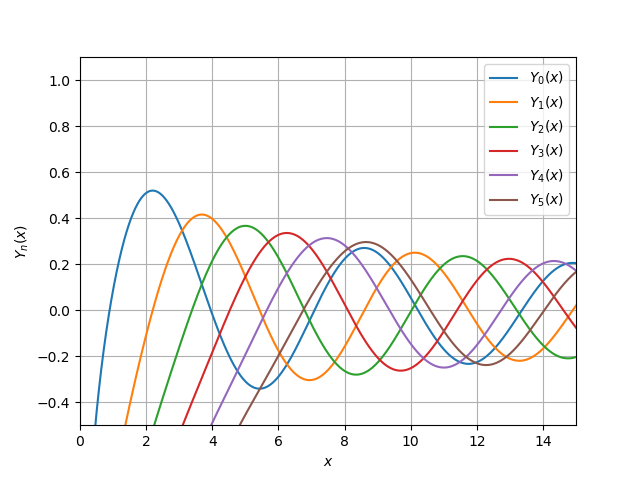
yv(v,x) import numpy as np import pylab as py import scipy.special as sp x = np.linspace(0, 15, 500000) for v in range(0, 6): py.plot(x, sp.yv(v, x)) py.xlim((0, 15)) py.ylim((-0.5, 1.1)) py.legend(('$Y_{0}(x)$', '$ Y_{1}(x)$', '$Y_{2}(x)$', '$Y_{3}(x)$', '$ Y_{4}(x)$','$ Y_{5}(x)$'), loc = 0) py.xlabel('$x$') py.ylabel('$Y_{n}(x)$') py.grid(True) py.show()
结论:
本文介绍了使用mpmath,sympy和scipy库处理贝塞尔函数的基础知识,并提供了使用函数求解微分方程的示例。 该文章可能对研究数学物理方程很有用。
参考文献:
1.
贝塞尔函数2.
使用拉普拉斯逆变换分析控制系统的动态链接3.
贝塞尔函数相关功能4.
特殊功能(scipy.special)。