在模拟变形的物理过程以及具有动态生成且可修改内容的游戏中，动态转换模型是一种常见的做法。 在这种情况下，可以方便地应用过程编辑和创建几何的方法。 后者通常允许在传输从网络下载的数据时节省珍贵的字节。 另外，这很有趣！
本文旨在介绍Unity中网格的过程处理技能。 我们将讨论转换和生成网格部分的操作。
我们用于3D模型程序编辑的绅士工具包包括三个基本操作：三角剖分，点移动，拉伸。 我们将详细讨论最后两个。 首先，考虑最简单的运动操作-移动顶点，旋转和缩放边缘和三角形。 然后，我们将介绍一种用于生成新几何的方法-拉伸操作。
在以前的出版物中，我们描述了用于处理3D模型数据的便捷结构。结构代号public static class CustomMeshPool { private static List<CustomMesh> Pool; private static int pointer; public static CustomMesh GetMesh(int id) { return Pool[id]; } public static int Push(CustomMesh customMesh) { if (Pool == null) Pool = new List<CustomMesh>(); pointer = GetAvailableIndex(); if (pointer < Pool.Count) Pool[pointer] = customMesh; else Pool.Add(customMesh); return pointer; } public static bool Remove(int index) { if (Pool == null) return false; var b = Pool[index] == null; Pool[index] = null; return b; } public static int GetAvailableIndex() { if (Pool == null) return 0; var availableIndex = Pool.FindIndex(mesh => mesh == null); return availableIndex != -1 ? availableIndex : Pool.Count; } public static void Flush() { if (Pool != null) Pool.Clear(); } } public class CustomMesh { public int Id; public Triangle[] Triangles; public Vector3[] vertices; public Vector3[] normals; public Vector2[] uv0, uv2; public Color[] colors; public CustomMesh(Vector3[] vertices, int[] triangles, Vector3[] normals, Vector2[] uv0, Vector2[] uv2, Color[] colors) { this.vertices = vertices; this.normals = normals; if (normals != null) for (var i = 0; i < this.normals.Length; i++) { this.normals[i] = this.normals[i].normalized; } this.uv0 = uv0; this.uv2 = uv2; this.colors = colors; var ptr = CustomMeshPool.GetAvailableIndex(); CustomMeshPool.Push(this); Id = ptr; Triangles = new Triangle[triangles.Length / 3]; Triangles = Triangles .AsParallel() .Select((t, i) => new Triangle(ptr, i, triangles[i * 3], triangles[i * 3 + 1], triangles[i * 3 + 2])) .ToArray(); } } public struct Triangle { private int _index; public int Index { get { return _index; } set { _index = value; if (_edges != null) { _edges[0].TriangleIndex = value; _edges[1].TriangleIndex = value; _edges[2].TriangleIndex = value; } } } private int _meshId; public int MeshId { get { return _meshId; } internal set { _meshId = value; } } private Edge[] _edges; public Edge[] Edges { get { return _edges; } set { if (value.Length == 3) { _edges = value; for (var i = 0; i < 3; i++) { _edges[i].TriangleIndex = _index; } } else throw new IndexOutOfRangeException(); } } public Vertex V0 { get { return Edges[0].v0; } set { if (value.MeshId != MeshId) throw new Exception("Not the same mesh"); Edges[0].v0 = value; Edges[2].v1 = value; } } public Vertex V1 { get { return Edges[1].v0; } set { if (value.MeshId != MeshId) throw new Exception("Not the same mesh"); Edges[1].v0 = value; Edges[0].v1 = value; } } public Vertex V2 { get { return Edges[2].v0; } set { if (value.MeshId != MeshId) throw new Exception("Not the same mesh"); Edges[2].v0 = value; Edges[1].v1 = value; } } public Triangle(int meshId, int index, int v0, int v1, int v2) { _index = index; _meshId = meshId; var edges = new Edge[3]; edges[0] = new Edge(meshId, index, v0, v1); edges[1] = new Edge(meshId, index, v1, v2); edges[2] = new Edge(meshId, index, v2, v0); _edges = edges; } } public struct Edge { public Vertex v0; public Vertex v1; private int _meshId; public int MeshId { get { return _meshId; } internal set { _meshId = value; } } private int _triangleIndex; public int TriangleIndex { get { return _triangleIndex; } internal set { _triangleIndex = value; } } public Edge(int meshId, int triangleIndex, int v0Index, int v1Index) { _meshId = meshId; _triangleIndex = triangleIndex; v0 = new Vertex() { MeshId = meshId, Index = v0Index }; v1 = new Vertex() { MeshId = meshId, Index = v1Index }; } } public struct Vertex { public int Index; private int _meshId; public int MeshId { get { return _meshId; } internal set { _meshId = value; } } public Vector3 position { get { return CustomMeshPool.GetMesh(_meshId).vertices[Index]; } set { CustomMeshPool.GetMesh(_meshId).vertices[Index] = value; } } public Vector3 normal { get { return CustomMeshPool.GetMesh(_meshId).normals[Index]; } set { CustomMeshPool.GetMesh(_meshId).normals[Index] = value; } } public Vector2 uv0 { get { return CustomMeshPool.GetMesh(_meshId).uv0[Index]; } set { CustomMeshPool.GetMesh(_meshId).uv0[Index] = value; } } public Vector2 uv2 { get { return CustomMeshPool.GetMesh(_meshId).uv2[Index]; } set { CustomMeshPool.GetMesh(_meshId).uv2[Index] = value; } } public Color color { get { return CustomMeshPool.GetMesh(_meshId).colors[Index]; } set { CustomMeshPool.GetMesh(_meshId).colors[Index] = value; } } }
如您所见，此处使用了PLINQ。 这是因为计算几何算法通常可以通过多线程进行优化。
当然，与执行“手动”代码时相比，在LINQ构造执行期间创建的LINQ构造更多。 但是，这种设计的简洁性以及PLINQ中内置的资源管理工具的存在，在很大程度上弥补了这一缺点。 此外，单线程和多线程实现之间的转换仅用一个命令即可完成，这极大地简化了调试过程。我扭曲，扭曲，我想混淆
我们继续运动的运作。 移动顶点没有什么复杂的。 只是不要忘了同时出现的高峰：如果需要，它们的位置也应该改变。
该算法是通过将运动矢量添加到顶点位置来实现的。 相对于模型的原点（
枢轴 ）发生偏移。 值得注意的是，在这样的变换过程中多边形的位置可以改变，但是其顶点的法线不能改变。 但是，为了简化演示，我们将不考虑这种细微差别。
CAD工具具有重新计算法线的功能，通常在应用所需的转换后会调用此功能。 有多种方法可以进行此分配。 最常见的方法是计算每个三角形的平面的法线，然后为每个顶点分配一个法线作为该顶点所属三角形的法线的平均值。通常，没有充分的理由使代码复杂化并应用转换矩阵。 将运动矢量添加到顶点位置的结果对应于其运动的直观概念。
列出移动一个顶点的方法 public struct Vertex { ... public void Translate(Vector3 movement, bool withCoincident = false) { var newPosition = position + movement; if (withCoincident) { var vertices = CustomMeshPool.GetMesh(_meshId).vertices; var mask = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(position); for (int i = 0; i < vertices.Length; i++) if (mask[i]) vertices[i] = newPosition; } else { position = newPosition; } } } public class CustomMesh { … public bool[] GetVerticesInPosition(Vector3 position) { bool[] buffer = new bool[vertices.Length]; for (int i = 0; i < buffer.Length; i++) { buffer[i] = Mathf.Abs(position.x - vertices[i].x) < Mathf.Epsilon && Mathf.Abs(position.y - vertices[i].y) < Mathf.Epsilon && Mathf.Abs(position.z - vertices[i].z) < Mathf.Epsilon; } return buffer; } }
边缘和三角形的移动以相同的方式实现-通过添加位移矢量。
列出移动三角形和边缘的方法 public struct Edge { … public void Translate(Vector3 movement, bool withCoincident = false) { if (withCoincident) { var vertices = CustomMeshPool.GetMesh(MeshId).vertices; var newV0Position = v0.position + movement; var newV1Position = v1.position + movement; var maskV0 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v0.position); var maskV1 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v1.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; } } else { v0.Translate(movement); v1.Translate(movement); } } } public struct Triangle { … public void Translate(Vector3 movement, bool withCoincident = false) { if (withCoincident) { var vertices = CustomMeshPool.GetMesh(_meshId).vertices; var newV0Position = V0.position + movement; var newV1Position = V1.position + movement; var newV2Position = V2.position + movement; var maskV0 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V0.position); var maskV1 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V1.position); var maskV2 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V2.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; else if (maskV2[i]) vertices[i] = newV2Position; } } else { V0.Translate(movement); V1.Translate(movement); V2.Translate(movement); } } }
但是使用
转换矩阵进行旋转和缩放更方便。 这些操作相对于模型坐标原点的结果很可能不是您期望或想要看到的。 旋转和缩放的参考点通常被视为对象的中间，这是人类最容易理解的。
列出旋转和缩放三角形和边的方法 public struct Edge { … public void Rotate(Quaternion rotation, bool withCoincident = false) { var pivot = (v0.position + v1.position) * 0.5f; var matrix = Matrix4x4.TRS(pivot, rotation, Vector3.one); var newV0Position = matrix.MultiplyPoint(v0.position - pivot); var newV1Position = matrix.MultiplyPoint(v1.position - pivot); if (withCoincident) { var vertices = CustomMeshPool.GetMesh(MeshId).vertices; var maskV0 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v0.position); var maskV1 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v1.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; } } else { v0.position = newV0Position; v1.position = newV1Position; } } public void Scale(Vector3 scale, bool withCoincident = false) { var pivot = (v0.position + v1.position) * 0.5f; var matrix = Matrix4x4.TRS(pivot, Quaternion.identity, scale); var newV0Position = matrix.MultiplyPoint(v0.position - pivot); var newV1Position = matrix.MultiplyPoint(v1.position - pivot); if (withCoincident) { var vertices = CustomMeshPool.GetMesh(MeshId).vertices; var maskV0 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v0.position); var maskV1 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v1.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; } } else { v0.position = newV0Position; v1.position = newV1Position; } } } public struct Triangle { … public void Rotate(Quaternion rotation, bool withCoincident = false) { var pivot = (V0.position + V1.position + V2.position) / 3; var matrix = Matrix4x4.TRS(Vector3.zero, rotation, Vector3.one); var newV0Position = matrix.MultiplyPoint(V0.position - pivot) + pivot; var newV1Position = matrix.MultiplyPoint(V1.position - pivot) + pivot; var newV2Position = matrix.MultiplyPoint(V2.position - pivot) + pivot; if (withCoincident) { var vertices = CustomMeshPool.GetMesh(_meshId).vertices; var maskV0 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V0.position); var maskV1 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V1.position); var maskV2 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V2.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; else if (maskV2[i]) vertices[i] = newV2Position; } } else { Edges[0].v0.position = newV0Position; Edges[1].v0.position = newV1Position; Edges[2].v0.position = newV2Position; } Edges[0].v0.normal = matrix.MultiplyPoint(V0.normal); Edges[1].v0.normal = matrix.MultiplyPoint(V1.normal); Edges[2].v0.normal = matrix.MultiplyPoint(V2.normal); } public void Scale(Vector3 scale, bool withCoincident = false) { var pivot = (V0.position + V1.position + V2.position) / 3; var matrix = Matrix4x4.TRS(pivot, Quaternion.identity, scale); var newV0Position = matrix.MultiplyPoint(V0.position - pivot); var newV1Position = matrix.MultiplyPoint(V1.position - pivot); var newV2Position = matrix.MultiplyPoint(V2.position - pivot); if (withCoincident) { var vertices = CustomMeshPool.GetMesh(_meshId).vertices; var maskV0 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V0.position); var maskV1 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V1.position); var maskV2 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V2.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; else if (maskV2[i]) vertices[i] = newV2Position; } } else { Edges[0].v0.position = newV0Position; Edges[1].v0.position = newV1Position; Edges[2].v0.position = newV2Position; } } }
为自己铺上一个整洁的洞
在3D建模中，经常使用拉伸操作。 对于其实现，必须知道运动矢量（位移）和多边形集。 挤出过程可以分解为两个步骤：
1.多边形的偏移量为给定的运动矢量（
offset ）。 在这种情况下，必须复制由边界多边形分隔的顶点，以免干扰那些不属于位移部分的元素的位置。 换句话说，您需要撕开并移动选定的片段。 如果首先完成此步骤，则模型可能会分解为将来必须结合的部分。
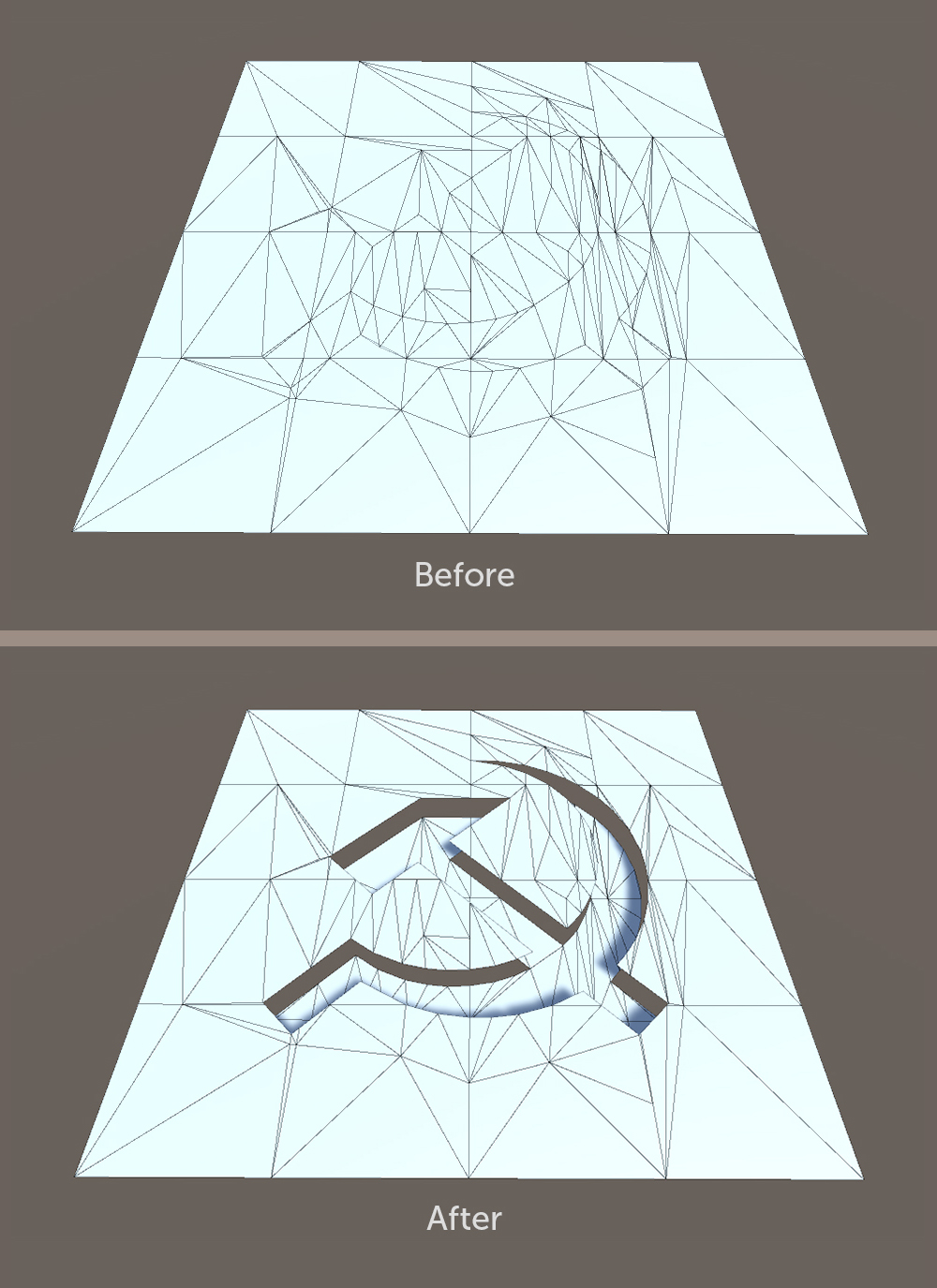
2.在位移零件的边界和挤压过程中形成的边界之间添加新的几何形状。 模型的主要部分和移动部分之间的间隙填充有形成墙的多边形。
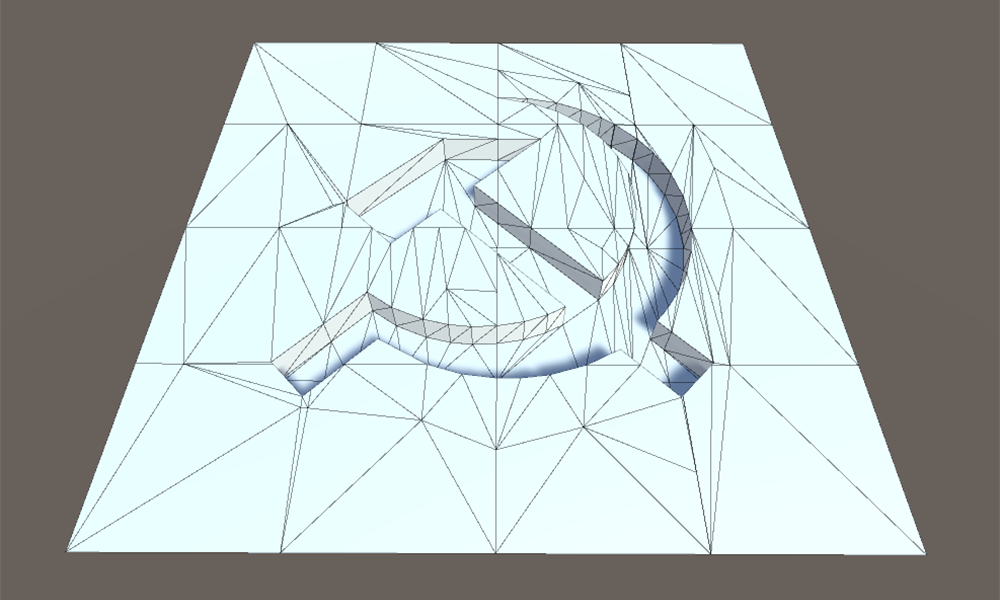
在实现中，首先构建墙是更方便的，因为在移位之前，我们具有边界上边缘的初始位置，并且可以立即使用此数据。 否则，您将不得不反转剪切矢量的方向，或者保存一些有关网格初始状态的信息。
我们使用的模型及其零件由成对的相邻多边形（三角形）组成。 我们称每个这样的集合为
簇 。
Blender中的两个专用集群
首先，我们需要获取限制所选聚类的轮廓的所有边缘。 为此，只需将边缘顺序添加到列表中即可。 如果找到匹配的边，则必须在不添加当前边的情况下将其删除。 为了使这种算法正确运行，有必要引入一个限制：在所选的三角形集合上，存在不超过两个重合的边。 在使用
拉伸的情况下，模型通常会满足此条件，并且更复杂的算法需要大量的计算资源。
列出获取轮廓轮廓边的方法 internal static class LinkedListExtension { internal static IEnumerable<LinkedListNode<T>> Nodes<T>(this LinkedList<T> list) { for (var node = list.First; node != null; node = node.Next) { yield return node; } } } public struct Vertex { … public bool IsInPosition(Vector3 other) { return Mathf.Abs(position.x - other.x) < Mathf.Epsilon && Mathf.Abs(position.y - other.y) < Mathf.Epsilon && Mathf.Abs(position.z - other.z) < Mathf.Epsilon; } } public struct Edge { … public bool Coincides(Edge other, bool includeDirection = false) { return v0.IsInPosition(other.v0.position) && v1.IsInPosition(other.v1.position) || !includeDirection && v1.IsInPosition(other.v0.position) && v0.IsInPosition(other.v1.position); } } public class CustomMesh { … private LinkedList<Edge> ObtainHullEdges(int[] triIndices) { var edges = new LinkedList<Edge>(); for (var i = 0; i < triIndices.Length; i++) { var edge = edges.Nodes().FirstOrDefault(e => e.Value.Coincides(Triangles[triIndices[i]].Edges[0])); if (edge != null) edges.Remove(edge); else edges.AddFirst(Triangles[triIndices[i]].Edges[0]); edge = edges.Nodes().FirstOrDefault(e => e.Value.Coincides(Triangles[triIndices[i]].Edges[1])); if (edge != null) edges.Remove(edge); else edges.AddFirst(Triangles[triIndices[i]].Edges[1]); edge = edges.Nodes().FirstOrDefault(e => e.Value.Coincides(Triangles[triIndices[i]].Edges[2])); if (edge != null) edges.Remove(edge); else edges.AddFirst(Triangles[triIndices[i]].Edges[2]); } return edges; } }
接收轮廓的所有边缘后，您需要构建相应的墙。 有许多实现方式，但是我们决定采用阻力最小的路径-分别基于边缘在运动矢量的方向上生成平行四边形。 由于我们所有人都只有一个位移，因此，平行四边形将为每个簇形成一个坚固的封闭壁。 仍然需要确定壁单元的方向。
墙像整个网格一样，由三角形组成。
根据OpenGL约定，如果在将其点投影到屏幕平面上时按顺序绕动它们对应于顺时针行走，则会在屏幕上呈现
一个单独的三角形：
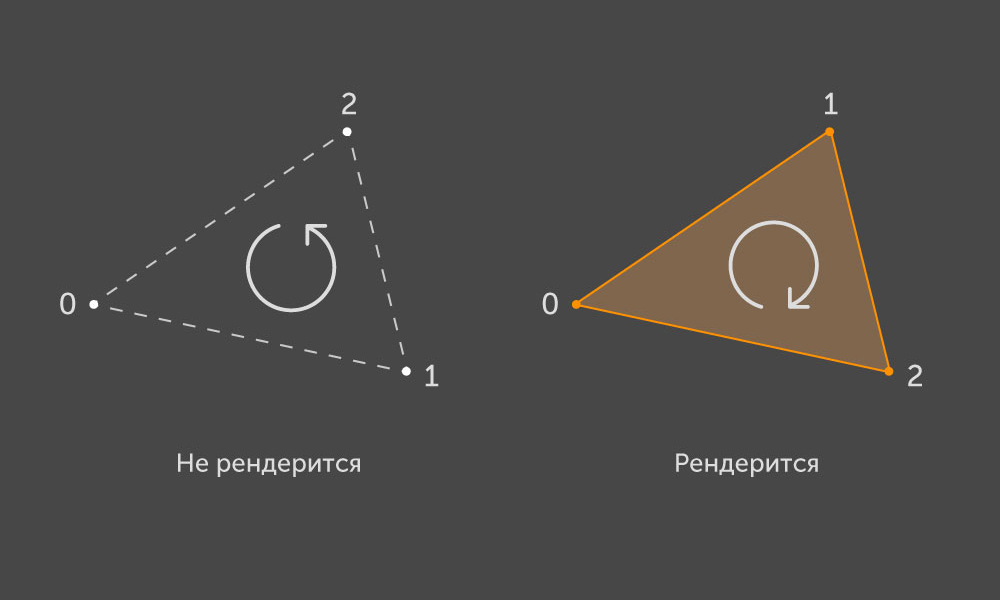
因此，三角形对应于定义正面的某个法向矢量。 每个三角形都由包含三个边的凸轮廓线界定。 每个边都有两个在我们的结构中表示为
v0和
v1的顶点。 我们定义边缘的方向，以使
v0为起点，
v1为终点。 现在，如果根据三角形的顶点的旁通设置了三角形边缘的方向，则群集的任何外部轮廓都必须具有顺时针或逆时针的旁通，而内部的任何轮廓都必须具有旁通（反之亦然）。 我们实现了
CustomMesh和
Triangle构造函数，以便所有三角形的顶点的遍历与顺时针方向相对应。
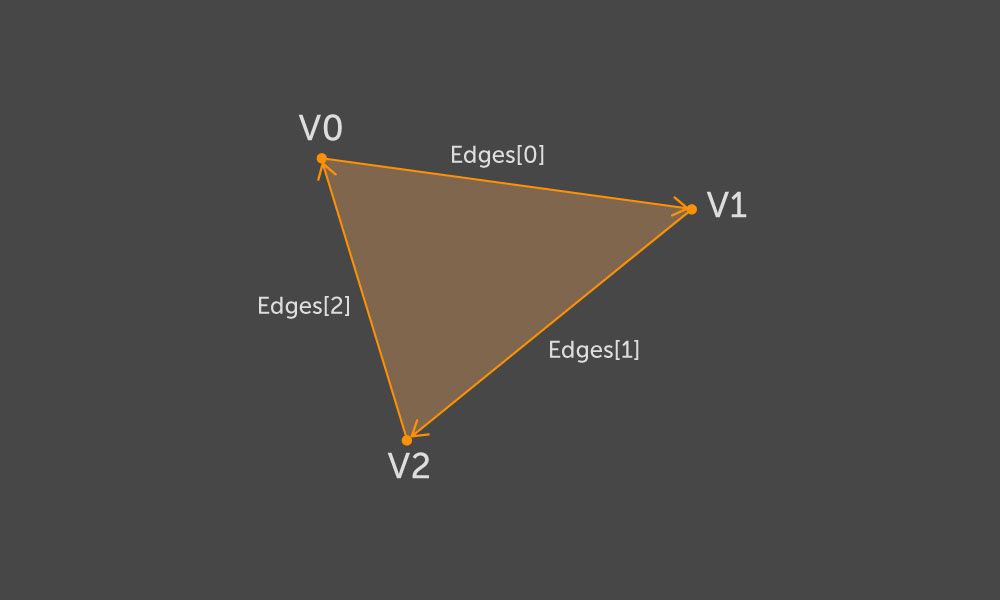
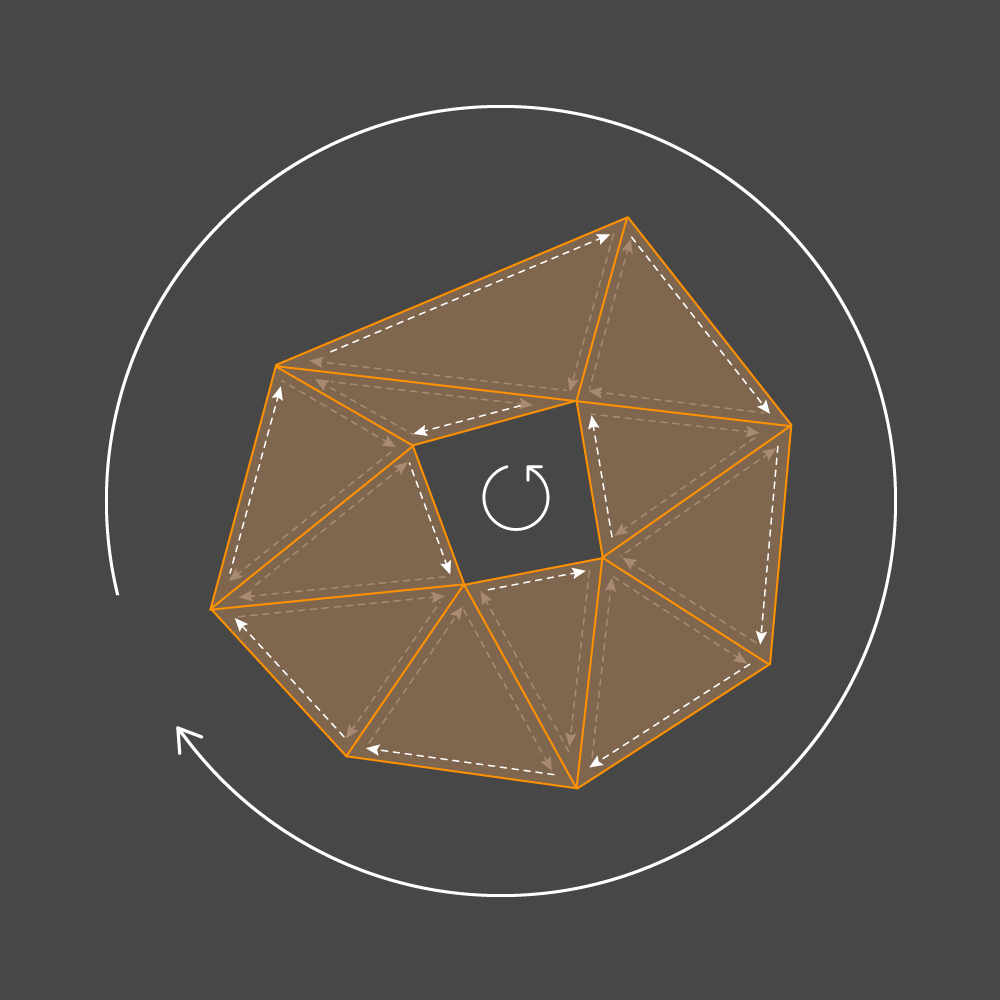
具有绕过轮廓的方向，我们可以确定地说肋的哪一侧是轮廓的内部，而哪一侧是轮廓的外部。 基于此信息，我们将选择墙的方向。 令（
v0，v1 ）为边缘，基于该边缘应生成所需的平行四边形。 我们将两个点
v2和
v3作为偏移位置
v0和
v1 。 然后根据以下方案构造两个三角形：
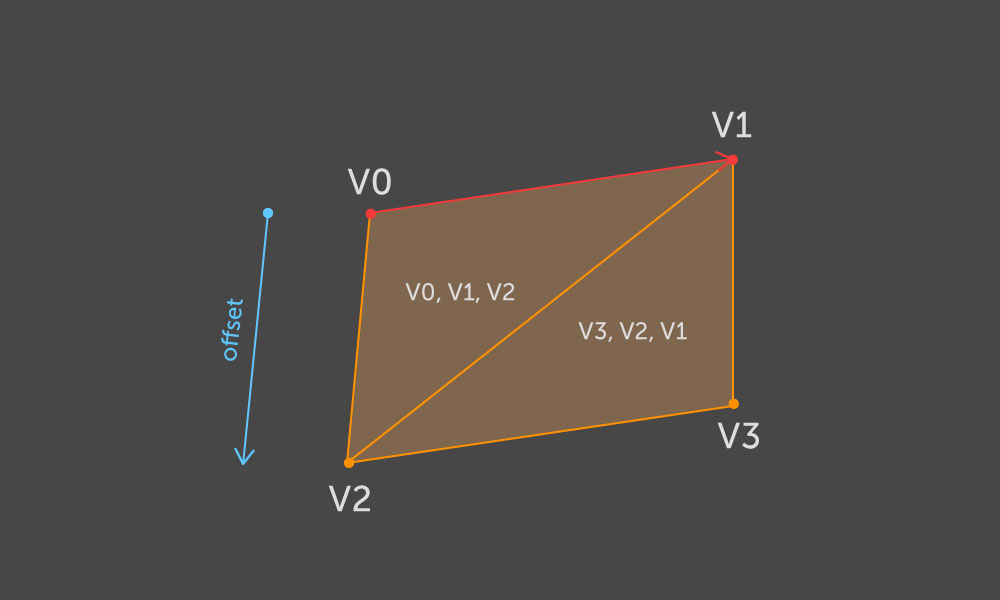
等高线的每个边缘。
列出使用边列表构造墙的方法 public class CustomMesh { … private void ExtrudeEdgesSet(Edge[] edges, Vector3 offset) { if (offset == Vector3.zero || edges == null || edges.Length == 0) return; var initVerticesLength = vertices.Length; Array.Resize(ref vertices, initVerticesLength + edges.Length * 4); if (normals != null && normals.Length == initVerticesLength) { Array.Resize(ref normals, vertices.Length); } if (uv0 != null && uv0.Length == initVerticesLength) { Array.Resize(ref uv0, vertices.Length); } if (uv2 != null && uv2.Length == initVerticesLength) { Array.Resize(ref uv2, vertices.Length); } if (colors != null && colors.Length == initVerticesLength) { Array.Resize(ref colors, vertices.Length); } var initTrianglesLength = Triangles.Length; Array.Resize(ref Triangles, initTrianglesLength + edges.Length * 2); edges .AsParallel() .Select((edge, i) => { int j = initVerticesLength + i * 4; vertices[j] = edge.v0.position; vertices[j + 1] = edge.v1.position; vertices[j + 2] = edge.v0.position + offset; vertices[j + 3] = edge.v1.position + offset; if (normals != null && normals.Length == vertices.Length) { var normal = Vector3.Cross(vertices[j + 1] - vertices[j], offset); normals[j] = normals[j + 1] = normals[j + 2] = normals[j + 3] = normal; } if (uv0 != null && uv0.Length == vertices.Length) { uv0[j] = uv0[j + 2] = edge.v0.uv0; uv0[j + 1] = uv0[j + 3] = edge.v1.uv0; } if (uv2 != null && uv2.Length == vertices.Length) { uv2[j] = uv2[j + 2] = edge.v0.uv2; uv2[j + 1] = uv2[j + 3] = edge.v1.uv2; } if (colors != null && colors.Length == vertices.Length) { colors[j] = colors[j + 2] = edge.v0.color; colors[j + 1] = colors[j + 3] = edge.v1.color; } Triangles[initTrianglesLength + i * 2] = new Triangle( initTrianglesLength + i * 2, Id, j, j + 1, j + 2 ); Triangles[initTrianglesLength + i * 2 + 1] = new Triangle( initTrianglesLength + i * 2 + 1, Id, j + 3, j + 2, j + 1 ); return true; }).ToArray(); } }
通过这种方法，生成的墙的前侧对于滑道和凹坑将是正确的。 仅存在一个重要的限制：在其上执行
拉伸操作的一组三角形不应该相对于运动矢量缠绕在其周围。
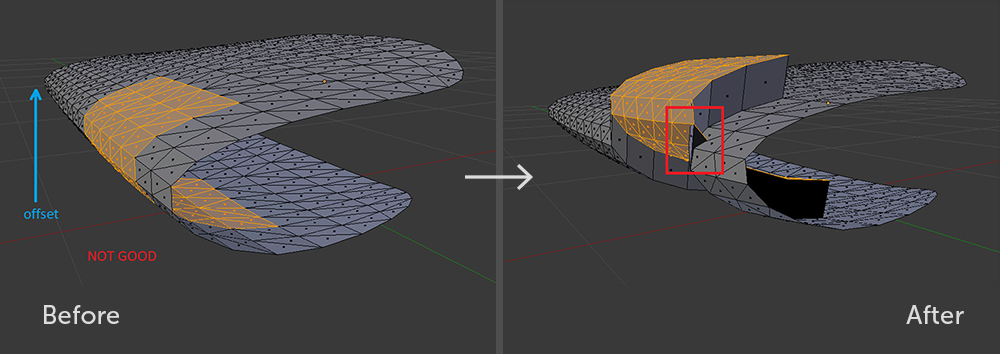关于偏移量无效的多边形子集。 即使在具有这种拉伸的Blender中 ，也无法避免几何曲线
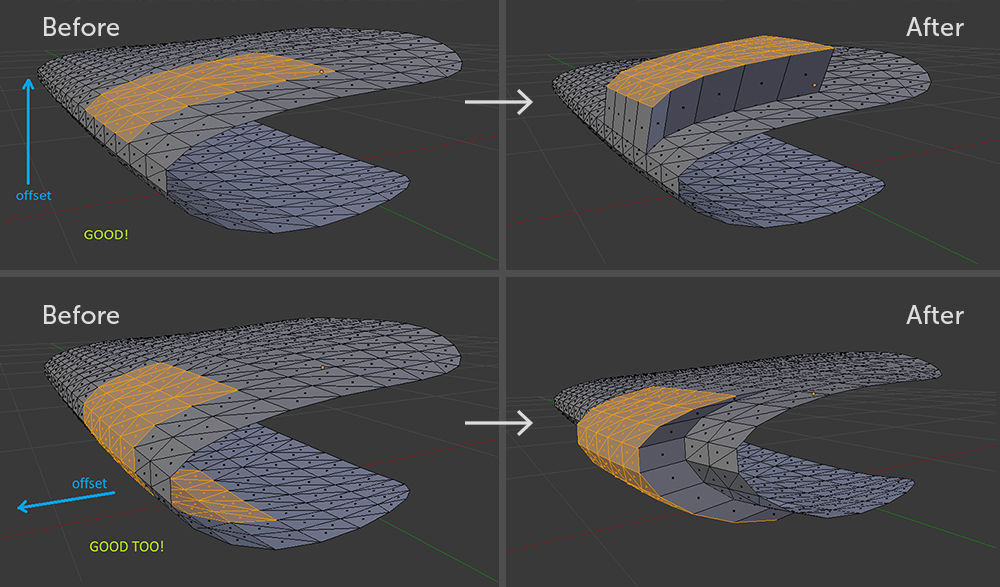有效的多边形子集墙已经准备好了，它仍然可以移动三角形。 算法的这一步很容易理解，尽管实现起来很麻烦。
在我们的例子中，我们需要确保簇的每个顶点仅属于其三角形。 如果不满足该条件，则一些相邻的多边形可以到达该群集。 解决这种情况的方法是复制属于群集和模型其余部分的每个顶点。 然后，对于群集中的所有多边形，将此顶点的索引替换为重复索引。 当条件满足时，我们将群集的所有顶点移到运动矢量。
列出移动多边形簇的方法 public class CustomMesh { … private void TranslateTrianglesHard(int[] triIndices, Vector3 offset, int[] hullVerts) { var newVertexIndices = new Dictionary<int, int>(); var initVerticesCount = vertices.Length; Triangles.Where((t, i) => !triIndices.Contains(i)).Select(t => { if (hullVerts.Contains(t.V0.Index) && !newVertexIndices.ContainsKey(t.V0.Index)) newVertexIndices.Add(t.V0.Index, initVerticesCount + newVertexIndices.Count); if (hullVerts.Contains(t.V1.Index) && !newVertexIndices.ContainsKey(t.V1.Index)) newVertexIndices.Add(t.V1.Index, initVerticesCount + newVertexIndices.Count); if (hullVerts.Contains(t.V2.Index) && !newVertexIndices.ContainsKey(t.V2.Index)) newVertexIndices.Add(t.V2.Index, initVerticesCount + newVertexIndices.Count); return false; }).ToArray(); Array.Resize(ref vertices, initVerticesCount + newVertexIndices.Count); foreach (var pair in newVertexIndices) vertices[pair.Value] = vertices[pair.Key] + offset; if (normals != null && normals.Length == initVerticesCount) { Array.Resize(ref normals, vertices.Length); foreach (var pair in newVertexIndices) normals[pair.Value] = normals[pair.Key]; } if (uv0 != null && uv0.Length == initVerticesCount) { Array.Resize(ref uv0, vertices.Length); foreach (var pair in newVertexIndices) uv0[pair.Value] = uv0[pair.Key]; } if (uv2 != null && uv2.Length == initVerticesCount) { Array.Resize(ref uv2, vertices.Length); foreach (var pair in newVertexIndices) uv2[pair.Value] = uv2[pair.Key]; } if (colors != null && colors.Length == initVerticesCount) { Array.Resize(ref colors, vertices.Length); foreach (var pair in newVertexIndices) colors[pair.Value] = colors[pair.Key]; } var alreadyMoved = new HashSet<int>(); for (var i = 0; i < triIndices.Length; i++) { if (newVertexIndices.ContainsKey(Triangles[triIndices[i]].V0.Index)) { var index = newVertexIndices[Triangles[triIndices[i]].V0.Index]; Triangles[triIndices[i]].Edges[0].v0.Index = index; Triangles[triIndices[i]].Edges[2].v1.Index = index; } else if (!alreadyMoved.Contains(Triangles[triIndices[i]].V0.Index)) { vertices[Triangles[triIndices[i]].V0.Index] += offset; alreadyMoved.Add(Triangles[triIndices[i]].V0.Index); } if (newVertexIndices.ContainsKey(Triangles[triIndices[i]].V1.Index)) { var index = newVertexIndices[Triangles[triIndices[i]].V1.Index]; Triangles[triIndices[i]].Edges[0].v1.Index = index; Triangles[triIndices[i]].Edges[1].v0.Index = index; } else if (!alreadyMoved.Contains(Triangles[triIndices[i]].V1.Index)) { vertices[Triangles[triIndices[i]].V1.Index] += offset; alreadyMoved.Add(Triangles[triIndices[i]].V1.Index); } if (newVertexIndices.ContainsKey(Triangles[triIndices[i]].V2.Index)) { var index = newVertexIndices[Triangles[triIndices[i]].V2.Index]; Triangles[triIndices[i]].Edges[1].v1.Index = index; Triangles[triIndices[i]].Edges[2].v0.Index = index; } else if (!alreadyMoved.Contains(Triangles[triIndices[i]].V2.Index)) { vertices[Triangles[triIndices[i]].V2.Index] += offset; alreadyMoved.Add(Triangles[triIndices[i]].V2.Index); } } } }
做完了 现在，将所有步骤的结果加起来，我们得到了一个洞或一个小山。
列出挤出操作的最终方法 public class CustomMesh { … public void ExtrudeTriangles(int[] triIndices, Vector3 offset) { var edges = ObtainHullEdges(triIndices); ExtrudeEdgesSet(edges.ToArray(), offset); var hullVertices = edges.Select(edge => edge.v0.Index).ToArray(); TranslateTrianglesHard(triIndices, offset, hullVertices); } }
使用纹理扫描的坐标和轮廓点的位移，您可以得到这样的凹口：
这还不是全部
除了上面讨论的编辑操作之外，我们还使用其他方便的方法来处理模型。
例如，我们另外编写了
Combine（）方法来组合两个
CustomMesh 。 我们的实现与
UnityEngine.Mesh.CombineMeshes（）之间的主要区别在于，如果在合并网格时某些顶点是完全等效的，则仅保留其中之一，从而避免了不必要的几何形状。
在同一模块中，我们实现
了Delaunay平面三角剖分算法 。 举例来说，使用它可以关闭使用
挤压成型的大洞，该洞带有带水纹理的平盖并得到一个湖：
好吧，整理出来！ 在下一篇文章中，我们将考虑将
.fbx导入
Unity的功能以及项目中模型验证的方法。