错误如何变成罪恶

一位城市传奇人物说，糖袋棒的创造者上吊后便自身亡，因为他得知消费者不会将它们分成两半，而是轻轻地将其撕掉。 当然不是这样，但是如果遵循这种逻辑，那么一个名叫威廉·高塞特（William Gosset）的英国吉尼斯啤酒爱好者不仅应该吊死自己，而且由于他在棺材中的旋转应该已经将地球钻到了正中央。 所有这些都是因为他以笔名“ Student”出版的标志性发明数十年来被灾难性地滥用了。

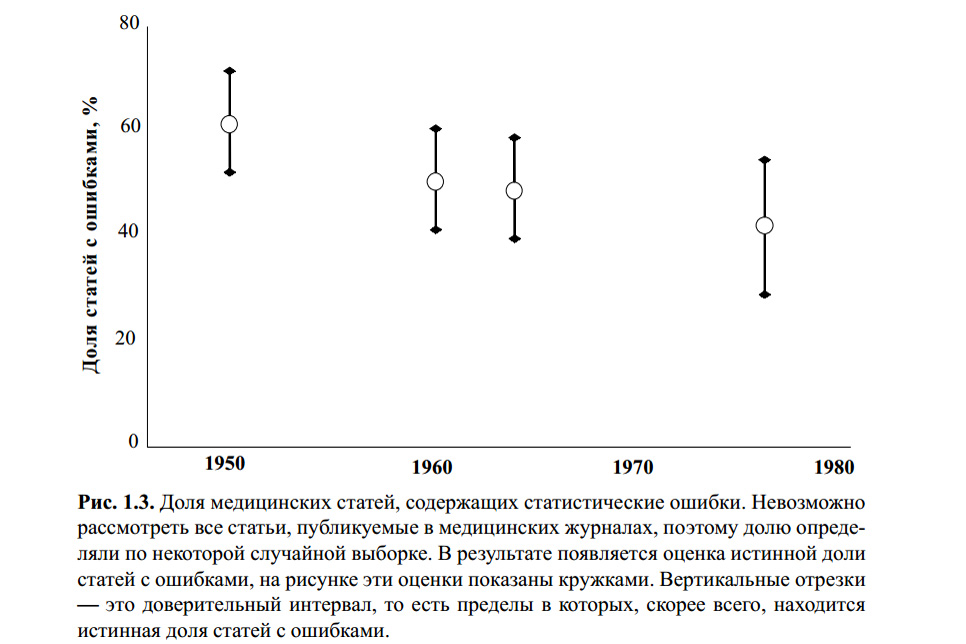
上图来自S. Glanz的书。 生物医学统计。 每 来自英语 -M.，《实践》，1998年。-459羽 我不知道是否有人检查过此表的统计错误。 但是，关于该主题的许多现代文章以及我的经验表明，无论有无，学生t准则仍然是最著名的，因此也是最受欢迎的。

这样做的原因是肤浅的教育（严格的教师教您需要“检查统计信息”，否则uuuuuu！），易于使用（表和在线计算器可用很多）以及平庸的不愿研究“如此有效”的事实。 大多数在学期论文甚至科学著作中至少使用过一次这一标准的人都会说：“好吧，我们比较了5名生气的学童和7名学童的游戏者的攻击性，我们在桌上的价值接近p = 0.05，这意味着游戏是邪恶的。嗯，是的，不完全是，但是有95％的概率。” 他们犯了多少逻辑和方法错误？

基础知识

学生t检验基于什么？ 逻辑取自贝叶斯定理，数学基础来自高斯分布，方法基于方差分析：

其中参数μ是分布的数学期望值（均值），参数σ是分布的标准偏差（σ²是方差）。

什么是方差分析？ 想象一个哈勃族的观众，按照某个年龄段的人数排序。 根据高斯函数，按年龄划分的人数可能会服从正态分布：

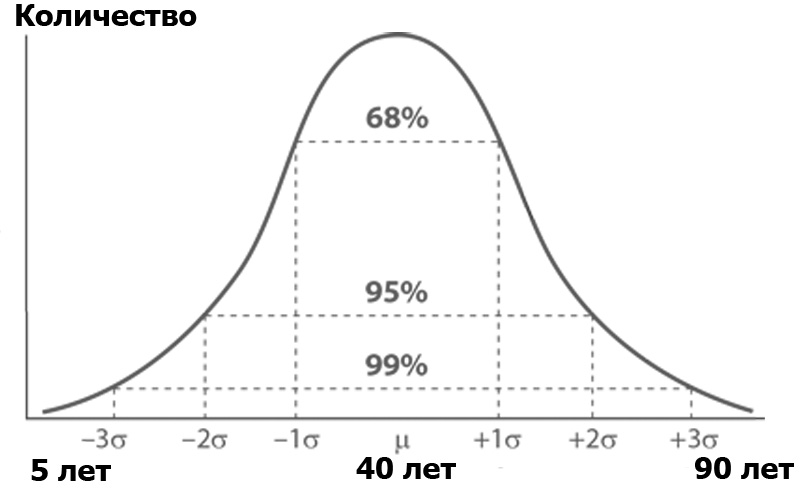
正态分布具有一个有趣的属性-几乎所有值都位于与平均值三个标准差的范围内。 标准偏差是多少？ 这是差异的根源。 色散是总人口中所有成员与平均数之差的平方之和除以这些成员的数量：

$$

$$σ_{n} ^ {2} = {\ frac {1} {n}} \和\极限_ {{i = 1}} ^ {n} \左（X_ {i}-{\ bar {X} } \对）^ {2}$$

也就是说，从平均值中减去每个值，平方以消除负号，然后取平均值，然后将其愚蠢地求和并除以这些值的数量。 结果是相对于平均值-方差的值的平均分散度的度量。

想象一下，我们在这个总体人群中选择了两个样本 ：Cryptocurrency中心的读者和Old Iron中心的读者。 通过随机抽样，我们总是得到接近正态的分布。 现在，我们在我们的人群中有了一个小的分销商：

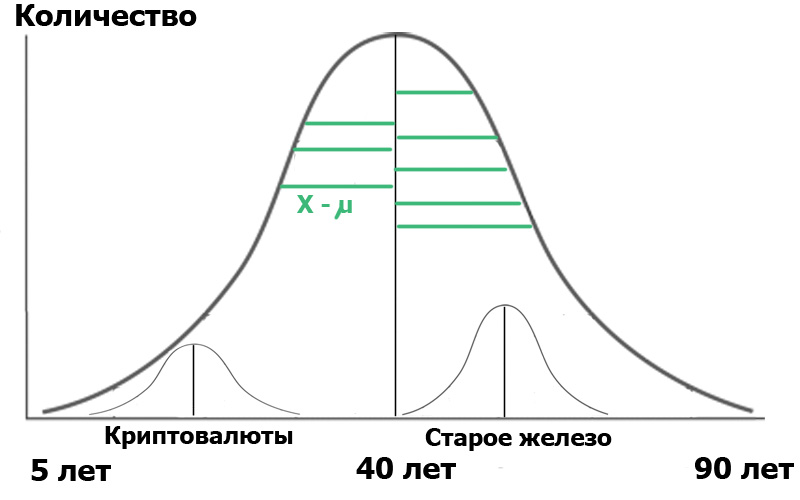
为了清楚起见，我显示了绿色部分-从分布点到平均值的距离。 如果将这些绿色段的长度平方，求和并求平均值，则这就是方差。

现在-注意。 我们可以通过这两个小样本来表征人口。 一方面，样本的方差表征了整个总体的方差。 另一方面，样本本身的平均值也是可以计算方差的数字！ 因此：我们得到了样本方差的平均值和样本平均值的方差 。

然后，我们可以进行方差分析，以逻辑公式的形式大致表示它：

$$

$$F = {\ frac {方差\：群体\：通过\：平均值\：值\：样本} {方差\：群体\：通过\：方差\：样本}}$$

上述公式会给我们带来什么？ 很简单 在统计中，所有这些都始于“零假设”，可以将其表述为“我们看来”，“所有巧合都是随机的”，即严格意义上的“两个观察到的事件之间没有联系”。 因此，在我们的案例中，零假设是在两个中心的用户年龄分布之间没有显着差异。 在原假设的情况下，我们的图将如下所示：

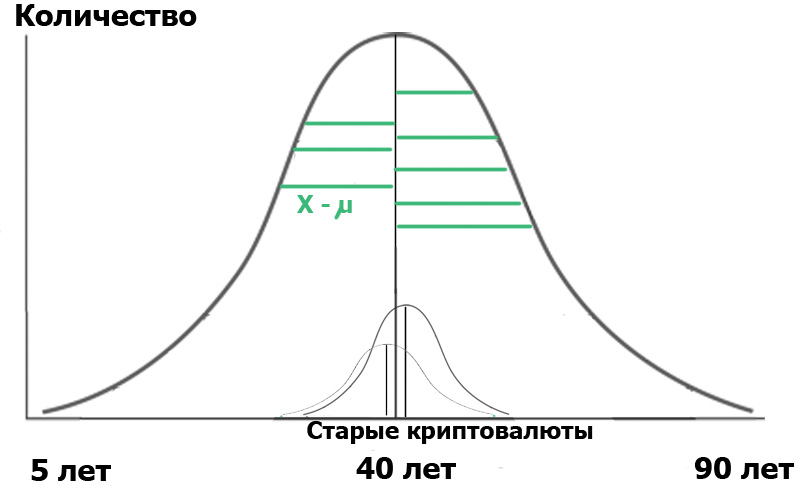
这意味着样本的方差和平均值均非常接近或相等，因此，总的来说，我们的准则

$$

$$F = {\ frac {方差\：群体\：通过\：平均值\：值\：样本} {方差\：群体\：通过\：方差\：样本}} = 1$$

但是，如果样本的方差相等，但是habrausers的年龄确实非常不同，则分子（平均值的方差）将很大，并且F将远远大于1。 然后该图将更像上图中。 它将给我们带来什么？ 没什么，如果您不注意措辞：无效假设将是没有重大差异。

但是意义……我们自己设定。 它表示为α，并且具有以下含义： 显着性水平是错误拒绝无效假设的最大可接受概率 。 换句话说，只有当我们的错误概率P小于α时，我们才将我们的事件视为一组之间的重大差异。 这是臭名昭著的p <0.05，因为通常在生物医学研究中，显着性水平定为5％。

好吧，那么一切都很简单。 取决于α，存在F的临界值，从这些临界值开始，我们将拒绝原假设。 它们以表格的形式发布，我们已经习惯使用它们了。 这是用于方差分析。 那学生呢？

学生说

学生标准只是方差分析的一种特殊情况。 再说一次，我不会用容易用谷歌搜索的公式让您超载，但我将传达其实质：

$$

$$t = {\ frac {差\：平均值\：值\：样本} {标准\：误差\：差异\：样本\：平均值}}$$

因此，所有这些冗长的解释都必须非常粗鲁和流利，但要清楚地表明t标准的基础。 因此，从其固有特性出发，直接遵循了其使用的局限性，即使是专业科学家也常常在其上犯错。

属性一：分布的正态性。

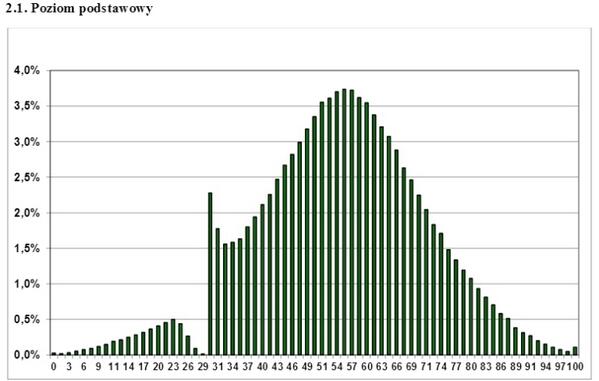
这是几年来作为波兰国家考试成绩在互联网上分布情况的图表。 从中可以得出什么结论？ 那考试没有通过，只是完全击退了Gopnik？ 哪些老师能“触及”学生？ 不，只有一个-对于非正态分布，您不能应用参数分析标准，例如Student。 如果您有一张单面的，锯齿状的，波浪形的，离散的分布图-忘记t标准，就不能使用它。 但是，即使通过认真的科学研究，有时也可以成功地忽略这一点。

在这种情况下该怎么办？ 使用所谓的非参数分析标准。 他们实现了另一种方法，即对数据进行排名，即从每个点的值移到分配给它的排名。 这些标准的准确性不如参数标准，但与不规范使用异常人群的参数标准相比，至少它们的使用是正确的。 在这些标准中，曼恩·惠特尼（Mann-Whitney）U标准最为人所知，通常被用作“小样本”的标准。 是的，它允许您处理最多5分的样本，但这已经很清楚了，但这并不是其主要目的。

第二个属性：您还记得公式吗？ F标准的值随样本平均值的差异（方差增加）而变化。 但是分母，即方差本身，不应改变。 因此，适用性的另一个标准应该是方差相等。 例如，在此说这种检查的频率更低了： 生物医学数据的统计分析错误。 列昂诺夫V.P. 国际医学实践杂志，2007年，第。 2，第19-35页 。

性质三：两个样品的比较。 他们喜欢使用t标准比较两个以上的群体。 通常这样进行：将A组与B组，B组与C组，A组与C.组之间的差异进行成对比较，然后在此基础上得出一定结论，这是绝对不正确的。 在这种情况下，产生了多个比较的效果。
在三个比较中的任何一个都获得了足够高的t值之后，研究人员报告说“ P <0.05”。 但实际上，错误的可能性大大超过了5％。

怎么了

我们计算出：例如，研究采用的显着性水平为5％。 这意味着在比较组A和B时错误拒绝无效假设的最大可接受概率为5％。 看来一切正确吗？ 但是在比较组B和C以及比较组A和C时也会发生完全相同的错误。 因此，通过这种评估整体上出错的可能性将不是5％，而是更高。 通常，此概率等于
P'= 1-（1-0.05）^ k
其中k是比较次数。

然后，在我们的研究中，拒绝原假设的错误概率约为15％。 比较这四个组时，对的数量以及因此可能的成对比较为6。因此，每个比较的显着性水平为0.05
错误地检测出至少一个差异的概率不再是0.05，而是0.31。

尽管如此，这个错误仍然不难消除。 一种方法是介绍Bonferroni修正案。 Bonferroni不等式告诉我们，如果您应用标准k次
在显着性水平为α的情况下，至少在一种情况下找到不存在差异的概率不超过k乘以α的乘积。 从这里：
α'<αk，
其中，α'是至少一次误认为差异的概率。 然后，我们的问题就非常简单地解决了：我们需要用Bonferroni校正（即，比较的多重性）来划分我们的显着性水平。 对于三个比较，我们需要从t检验表中获取对应于α= 0.05 / 3 = 0.0167的值。 我重复一遍-这很简单，但是这项修正不能忽略。 顺便说一句，即使将t-criterion的值除以8不必要的严格，您也不应被这项修正所迷惑。

接下来是他们常常根本不注意到的“小事”。 我故意在此处不提供公式，以免降低文本的可读性，但应记住，在以下情况下，t标准的计算方式有所不同：

• 两个样本的大小不同（通常，请记住，一般情况下，我们使用两个样本标准的公式比较两组）；

  
  

• 相关样本的可用性。 在这种情况下，需要以不同的时间间隔测量一名患者的数据，实验前后的一组动物的数据等。

  
  

最后，为了使您可以想象发生的一切情况，我将提供有关t标准使用不当的最新数据。 这些数字是针对1998年和2008年一些中国科学期刊的，它们是不言而喻的。 我真的希望这比不正确的科学数据在设计上更加粗心：

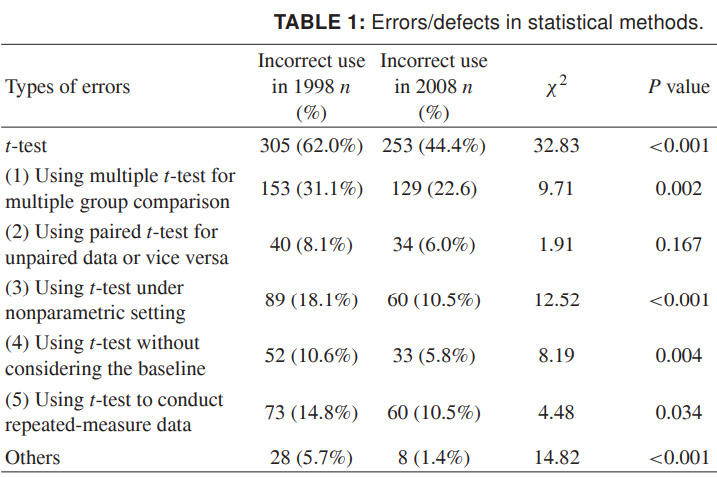
资料来源： 1998年和2008年10种主要中医期刊的统计方法滥用。吴顺权等，《科学世界》，2011，11，2106–2114

请记住，结果的低重要性不是错误结果，而是可悲的事情。 通过错误地应用统计数据扭曲数据是不可能带来科学罪过的-错误的结论。

关于统计数据的逻辑解释，包括错误的解释，我可能会分别讲述。

正确阅读。