山地车：通过强化训练解决经典挑战

通常，对依赖于特定任务的特定功能的算法的修改被认为价值不高，因为它们很难推广到更广泛的问题类别。 但是，这并不意味着不需要此类修改。 而且，即使对于简单的经典问题，它们通常也可以显着改善结果，这在算法的实际应用中非常重要。 例如，在这篇文章中，我将通过强化训练来解决“山地车”问题，并表明利用有关任务组织方式的知识，可以更快地解决该问题。

关于我自己

我叫Oleg Svidchenko，现在我在圣彼得堡HSE的物理，数学和计算机科学学院学习，然后在圣彼得堡大学学习了三年。 我还在JetBrains Research担任研究员。 在进入大学之前，我曾在莫斯科国立大学的SSC学习，并成为莫斯科团队中全俄计算机科学奥林匹克竞赛的获胜者。

我们需要什么？

如果您有兴趣尝试进行强化训练，那么“山地车”挑战就是一个很好的选择。 今天，我们需要具有安装好的 Gym和PyTorch库以及神经网络基础知识的Python。

任务说明

在二维世界中，汽车需要从两个山丘之间的凹陷处爬到右山丘的顶部。 由于她没有足够的发动机动力来克服重力并在第一次尝试时进入该重力，这一事实使情况变得复杂。 我们被邀请训练一个特工（在我们的例子中是一个神经网络），他可以通过控制它来尽快爬上正确的山坡。

机器控制是通过与环境的交互来执行的。 它分为独立的情节，每个情节都是逐步进行的。 在每个步骤，代理响应于动作a从环境接收状态s和环境r 。 另外，有时媒体可能会另外报告该情节结束。 在这个问题中， s是一对数字，第一个是汽车在弯道上的位置（一个坐标就足够了，因为我们不能将自己从曲面上撕开），第二个是它在曲面上的速度（带符号）。 奖励r是一个始终等于-1的数字。 通过这种方式，我们鼓励特工尽快完成剧集。 只有三种可能的动作：将汽车向左推，什么也不做，然后将汽车向右推。 这些动作对应于从0到2的数字。如果汽车到达右山顶或特工已采取200步，则该事件可能会结束。

一点理论

在哈布雷（Habré）上已经有一篇有关DQN的文章 ，作者在其中很好地描述了所有必要的理论。 不过，为了便于阅读，我将在这里以更正式的形式重复它。

强化学习任务由一组状态空间S，动作空间A，系数 $$$\伽玛$，过渡函数T和奖励函数R。通常，过渡函数和奖励函数可以是随机变量，但是现在我们将考虑一个更简单的版本，在其中对其进行唯一定义。 目标是最大化累积奖励。 $$$\ sum_ {t = 0} ^ {T} r_ {t} \ cdot \ gamma ^ {t}$，其中t是媒体中的步数，T是情节中的步数。

为了解决这个问题，假设我们从状态s开始，我们将状态s的值函数V定义为最大累积奖励的值。 知道了这样一个函数，我们可以简单地通过在每一步将s传递给s来获得最大可能值来解决问题。 但是，并非一切都那么简单：在大多数情况下，我们不知道采取什么行动会使我们达到理想的状态。 因此，我们将动作a添加为函数的第二个参数。 所得函数称为Q函数。 它显示了通过在状态s中执行动作a可以获得的最大可能累积奖励。 但是我们已经可以使用此功能解决问题：处于状态s时，我们只需选择一个使得Q（s，a）为最大。

实际上，我们不知道真正的Q函数，但是可以通过各种方法对其进行近似。 一种这样的技术是深度Q网络（DQN）。 他的想法是，对于每个动作，我们都使用神经网络来逼近Q函数。

环境

现在开始练习。 首先，我们需要学习如何模拟MountainCar环境。 健身房图书馆提供大量标准的强化学习环境，将帮助我们应对这一任务。 要创建环境，我们需要在Gym模块上调用make方法，将所需环境的名称作为参数传递给它：

import gym env = gym.make("MountainCar-v0") 

在此处可以找到详细的文档，并在此处可以找到有关环境的说明。
让我们更详细地考虑如何对创建的环境执行以下操作：

• env.reset() -结束当前情节并开始新的情节。 返回初始状态。
• env.step(action) -执行指定的操作。 返回新状态，奖励，情节是否已结束以及可用于调试的其他信息。
• env.seed(seed) -设置随机种子。 这取决于在env.reset（）期间如何生成初始状态。
• env.render() -显示环境的当前状态。

我们实现DQN

DQN是一种使用神经网络评估Q函数的算法。 在原始文章中， DeepMind使用卷积神经网络定义了Atari游戏的标准架构。 与这些游戏不同，Mountain Car不会将图像用作状态，因此我们必须自己确定架构。

例如，一个具有两个隐藏层的架构，每个隐藏层包含32个神经元。 在每个隐藏层之后，我们将使用ReLU作为激活函数。 两个描述状态的数字被馈送到神经网络的输入，在输出处我们得到Q函数的估计。

 import torch.nn as nn model = nn.Sequential( nn.Linear(2, 32), nn.ReLU(), nn.Linear(32, 32), nn.ReLU(), nn.Linear(32, 3) ) target_model = copy.deepcopy(model) #    def init_weights(layer): if type(layer) == nn.Linear: nn.init.xavier_normal(layer.weight) model.apply(init_weights) 

由于我们将在GPU上训练神经网络，因此我们需要在此处加载网络：

 #     CPU,  “cuda”    “cpu” device = torch.device("cuda") model.to(device) target_model.to(device) 

设备变量将是全局变量，因为我们还需要加载数据。

我们还需要定义一个优化器，该优化器将使用梯度下降来更新模型权重。 是的，不止一个。

 optimizer = optim.Adam(model.parameters(), lr=0.00003) 

现在，我们声明一个函数，该函数将考虑误差函数，沿其的梯度并应用下降。 但是在此之前，您需要将数据从批处理下载到GPU：

 state, action, reward, next_state, done = batch #       state = torch.tensor(state).to(device).float() next_state = torch.tensor(next_state).to(device).float() reward = torch.tensor(reward).to(device).float() action = torch.tensor(action).to(device) done = torch.tensor(done).to(device) 

接下来，我们需要计算Q函数的实际值，但是，由于我们不知道它们的真实性，我们将通过以下状态的值来评估它们：

 target_q = torch.zeros(reward.size()[0]).float().to(device) with torch.no_grad(): #     Q-function    target_q = target_model(next_state).max(1)[0].view(-1) target_q[done] = 0 target_q = reward + target_q * gamma 

和当前的预测：

 q = model(state).gather(1, action.unsqueeze(1)) 

使用target_q和q，我们计算损失函数并更新模型：

 loss = F.smooth_l1_loss(q, target_q.unsqueeze(1)) #      optimizer.zero_grad() #     loss.backward() #   . ,       for param in model.parameters(): param.grad.data.clamp_(-1, 1) #    optimizer.step() 

由于模型仅考虑Q函数，并且不执行操作，因此我们需要确定将决定代理将执行哪些操作的功能。 作为决策算法，我们采用 $$$\ varepsilon$-贪婪的政治。 她的想法是，代理通常会贪婪地执行操作，选择Q函数的最大值，但是很有可能 $$$\ varepsilon$他将采取随机行动。 需要随机动作，以便算法可以检查那些仅在贪婪策略的指导下不会执行的动作-此过程称为探索。

 def select_action(state, epsilon, model): if random.random() < epsilon: return random.randint(0, 2) return model(torch.tensor(state).to(device).float().unsqueeze(0))[0].max(0)[1].view(1, 1).item() 

由于我们使用批处理来训练神经网络，因此我们需要一个缓冲区来存储与环境交互的经验，并从中选择批处理：

 class Memory: def __init__(self, capacity): self.capacity = capacity self.memory = [] self.position = 0 def push(self, element): """    """ if len(self.memory) < self.capacity: self.memory.append(None) self.memory[self.position] = element self.position = (self.position + 1) % self.capacity def sample(self, batch_size): """    """ return list(zip(*random.sample(self.memory, batch_size))) def __len__(self): return len(self.memory) 

天真的决定

首先，声明我们将在学习过程中使用的常量，并创建一个模型：

 #  model   target model target_update = 1000 #  ,      batch_size = 128 #   max_steps = 100001 #  exploration max_epsilon = 0.5 min_epsilon = 0.1 #    memory = Memory(5000) model, target_model, optimizer = create_new_model() 

尽管将交互过程划分为几集是合乎逻辑的，但为了描述学习过程，将其划分为单独的步骤对于我们来说更为方便，因为我们希望在环境的每一步之后都采取梯度下降的一步。

让我们详细讨论一下学习的第一步。 我们假设现在正在使用max_steps步骤的步骤数和当前状态进行操作。 然后用 $$$\ varepsilon$-贪婪策略如下所示：

 epsilon = max_epsilon - (max_epsilon - min_epsilon)* step / max_steps action = select_action(state, epsilon, model) new_state, reward, done, _ = env.step(action) 

立即将获得的经验添加到内存中，如果当前的情节已经结束，则开始新的情节：

 memory.push((state, action, reward, new_state, done)) if done: state = env.reset() done = False else: state = new_state 

我们将采取梯度下降的步骤（当然，如果我们已经可以收集至少一批）：

 if step > batch_size: fit(memory.sample(batch_size), model, target_model, optimizer) 

现在仍然需要更新target_model：

 if step % target_update == 0: target_model = copy.deepcopy(model) 

但是，我们也希望遵循学习过程。 为此，我们将在每次更新epsilon = 0的target_model之后播放另外一集，将总奖励存储在rewards_by_target_updates缓冲区中：

 if step % target_update == 0: target_model = copy.deepcopy(model) state = env.reset() total_reward = 0 while not done: action = select_action(state, 0, target_model) state, reward, done, _ = env.step(action) total_reward += reward done = False state = env.reset() rewards_by_target_updates.append(total_reward) 

运行以下代码，并获得如下图所示的内容：

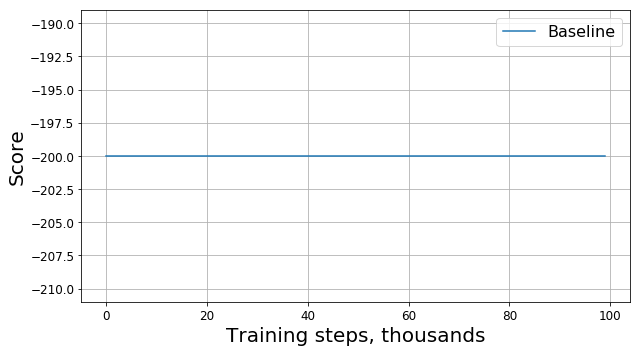
怎么了？

这是一个错误吗？ 这是错误的算法吗？ 这些参数不好吗？ 不完全是 实际上，问题出在任务上，即奖赏的功能上。 让我们仔细看看。 在每个步骤中，我们的特工都会得到-1的奖励，这种奖励一直持续到情节结束为止。 这样的奖励激励特工尽快完成情节，但同时并没有告诉他该如何做。 因此，学习如何解决此类代理问题的唯一方法就是使用探索多次解决问题。

当然，可以尝试使用更复杂的算法而不是我们的算法来研究环境 $$$\ varepsilon$-贪婪的政策。 但是，首先，由于它们的应用，我们的模型将变得更加复杂，这是我们希望避免的；其次，并不是它们可以很好地完成此任务的事实。 相反，我们可以通过修改任务本身（即通过更改奖励功能）来消除问题的根源。 通过应用所谓的奖励塑造。

加快融合

我们的直觉知识告诉我们，爬上山需要加速。 速度越高，代理商越能解决问题。 您可以例如通过在奖励中添加具有一定系数的速度模块来告诉他：

  modified_reward =奖励+ 10 * abs（new_state [1]） 

因此，函数中的一条线适合

  memory.push（（状态，动作，奖励，new_state，完成）） 

应该由

  memory.push（（状态，动作，modified_reward，new_state，完成）） 

现在，让我们看一下新图表（它给出了未经修改的原始奖项）：


RS是“奖励塑形”的缩写。

这样做好吗？

进步是显而易见的：随着奖励开始与-200不同，我们的代理商显然学会了爬坡。 剩下的只有一个问题：如果改变奖励的功能，我们也改变了任务本身，我们发现的新问题的解决方案对旧问题有好处吗？

首先，我们了解在我们的案例中“善良”的含义。 解决问题的方法是，我们试图找到最佳策略-一种使事件总回报最大化的策略。 在这种情况下，我们可以用“最佳”一词代替“良好”，因为我们正在寻找它。 我们还乐观地希望我们的DQN迟早会找到修改后的问题的最佳解决方案，而不会陷入局部最大值。 因此，问题可以重新表述为：如果改变奖励的功能，我们也改变了问题本身，发现的新问题的最优解对旧问题是否最优？

事实证明，在一般情况下我们无法提供这种保证。 答案取决于我们如何精确地改变奖励的功能，如何更早地安排奖励以及如何安排环境本身。 幸运的是，有一篇文章的作者调查了奖励功能的变化如何影响所找到解决方案的最优性。

首先，他们发现了一整套基于潜在方法的“安全”更改： $$$R’= R +（\ gamma \ cdot \ Phi（新\ _state）-\ Phi（州））$在哪里 $$$\皮皮$-潜力，仅取决于状态。 对于此类功能，作者能够证明，如果新问题的解决方案是最优的，那么旧问题的解决方案也是最优的。

其次，作者表明对于任何其他 $$$R’= R + F（s，a）$存在这样的问题，即R奖励函数和更改后的问题的最优解，因此该解决方案对于原始问题不是最优的。 这意味着，如果我们使用的更改不基于潜在方法，我们将无法保证所找到解决方案的优良性。

因此，使用潜在函数修改奖励函数只能改变算法的收敛速度，而不会影响最终解决方案。

正确加速收敛

现在我们知道了如何安全地更改奖励，让我们尝试使用潜在方法而不是幼稚的启发式方法再次修改任务：

  modified_reward =奖励+ 300 *（gamma * abs（new_state [1]）-abs（状态[1]）） 

让我们看一下原始奖项的时间表：



事实证明，除了具有理论上的保证外，借助潜在功能修改奖励还可以显着改善结果，尤其是在早期阶段。 当然，有可能选择更多的最佳超参数（随机种子，伽玛和其他系数）来训练代理，但是奖励整形仍会显着提高模型的收敛速度。

后记

感谢您阅读到底！ 我希望您喜欢这种以实践为导向的小课程，以加强学习。 很明显，Mountain Car是一项“玩具”任务，但是，正如我们能够注意到的那样，从人的角度来看，教给代理商解决甚至是看似简单的任务也很困难。