大o

注意事项 缩写翻译，而不是用您自己的话说。
UPD：如评论中所述，示例并不完美。 作者并不是在寻找解决该问题的最佳方法，他的目的是解释“指尖”算法的复杂性。

需要使用大O表示法来描述算法的复杂性。 为此，使用了时间概念。 对于许多人来说，这个话题很可怕，程序员避免谈论“订货时间N”是很常见的事情。

如果您能够按照Big O评估代码，那么您很可能被视为“聪明人”。 而且很可能您将进行下一次面试。 您是否会被问到是否有可能将任何代码的复杂度降低到n log n而不是n ^ 2的问题。

资料结构

数据结构的选择取决于特定的任务：取决于数据的类型及其处理算法。 为某些类型的算法创建了各种数据结构（.NET或Java或Elixir）。

通常，选择一种或另一种结构，我们只是复制普遍接受的解决方案。 在大多数情况下，这就足够了。 但是实际上，如果不了解算法的复杂性，我们就无法做出明智的选择。 数据结构的主题只有在算法复杂之后才能通过。

在这里，我们将仅使用数字数组（就像在采访中一样）。 JavaScript示例。

让我们从最简单的开始：O（1）

取一个由5个数字组成的数组：

const nums = [1,2,3,4,5]; 

假设您需要获取第一个元素。 我们为此使用索引：

 const nums = [1,2,3,4,5]; const firstNumber = nums[0]; 

这个算法有多复杂？ 我们可以说：“一点也不复杂-只取数组的第一个元素。” 的确如此，但是根据输入所执行的操作数量（达到输入结果）来描述复杂性更为正确。

换句话说：随着输入参数数量的增加，多少操作将增加。

在我们的示例中，有5个输入参数，因为数组中有5个元素。 要获得结果，您需要执行一项操作（按索引获取一个元素）。 如果数组中有100个元素，将需要执行多少个操作？ 还是1000？ 还是十万？ 一样，只需要一个操作。

即：“对所有可能的输入数据执行一次操作”-O（1）。

O（1）可以理解为“ 1阶复杂度”（1阶）或“算法以恒定/恒定时间运行”（恒定时间）。

您已经猜到O（1）算法是最有效的。

迭代和“订购时间n”：O（n）

现在，让我们找到数组元素的总和：

 const nums = [1,2,3,4,5]; let sum = 0; for(let num of nums){ sum += num; } 

我们再次问自己：我们需要多少个输入操作？ 在这里您需要对所有元素进行排序，即 每个元素上的操作。 数组越大，操作越多。

使用大O表示法：O（n）或“ n阶（n阶）的复杂度”。 同样，这种算法被称为“线性”算法或“线性缩放”算法。

分析方法

我们可以使求和效率更高吗？ 通常不会。 而且，如果我们知道该数组保证从1开始，是否排序且没有间隙？ 然后我们可以应用公式S = n（n + 1）/ 2（其中n是数组的最后一个元素）：

 const sumContiguousArray = function(ary){ //get the last item const lastItem = ary[ary.length - 1]; //Gauss's trick return lastItem * (lastItem + 1) / 2; } const nums = [1,2,3,4,5]; const sumOfArray = sumContiguousArray(nums); 

这样的算法比O（n）有效得多，而且，它是在“恒定/恒定时间”执行的，即 它是O（1）。

实际上，有多个操作：您需要获取数组的长度，获取最后一个元素，执行乘法和除法。 那不是O（3）还是什么？ 用大O表示法，实际的步数并不重要，算法在恒定时间内运行很重要。

恒定时间算法始终为O（1）。 与线性算法相同，实际上，运算可以是O（n + 5），在Big O中，符号是O（n）。

不是最佳解决方案：O（n ^ 2）

让我们编写一个检查数组是否重复的函数。 嵌套循环解决方案：

 const hasDuplicates = function (num) { //loop the list, our O(n) op for (let i = 0; i < nums.length; i++) { const thisNum = nums[i]; //loop the list again, the O(n^2) op for (let j = 0; j < nums.length; j++) { //make sure we're not checking same number if (j !== i) { const otherNum = nums[j]; //if there's an equal value, return if (otherNum === thisNum) return true; } } } //if we're here, no dups return false; } const nums = [1, 2, 3, 4, 5, 5]; hasDuplicates(nums);//true 

我们已经知道数组迭代为O（n）。 我们有一个嵌套循环，对于每个元素，我们都会再次进行迭代-即 O（n ^ 2）或“ n阶复杂度”。

在同一集合上具有嵌套循环的算法始终为O（n ^ 2）。

“ log n的顺序的复杂度”：O（log n）

在上面的示例中，嵌套循环本身（如果不考虑嵌套的话）的复杂度为O（n），因为 它是数组元素的枚举。 一旦找到所需元素，即该循环结束。 实际上，并非所有元素都会被列举。 但是Big O符号总是考虑最坏的情况-您正在寻找的项目可能是最后一个。

在这里，嵌套循环用于搜索数组中的给定元素。 在某些条件下，可以优化数组中元素的搜索-比线性O（n）更好。

让数组排序。 然后，我们可以使用二进制搜索算法：将数组分为两半，丢弃不必要的部分，再将剩余部分分为两部分，依此类推，直到找到所需的值。 这种算法称为分而治之分而治之。



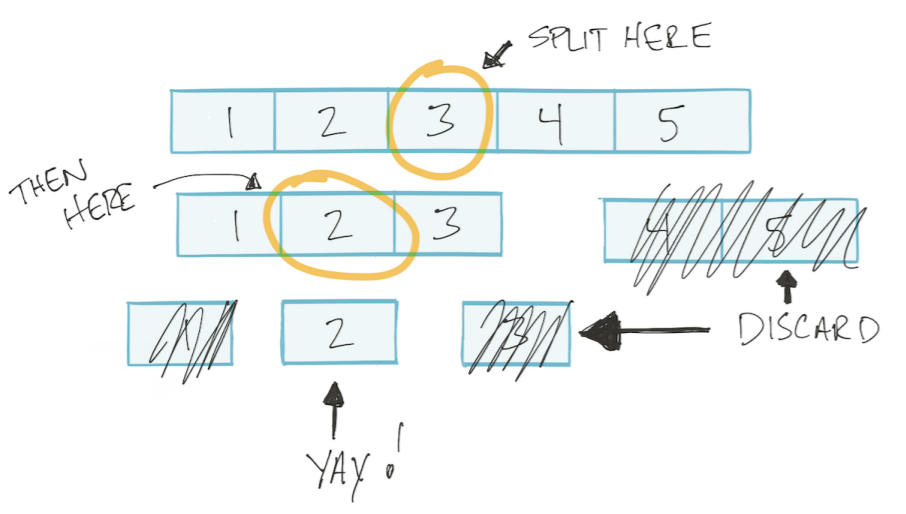
该算法基于对数。

对数快速概述

考虑一个例子，x等于什么？

x ^ 3 = 8

我们需要取8的立方根-这将是2。现在更加困难

2 ^ x = 512

使用对数，问题可以写成

log2（512）= x

“ 512的以2为底的对数是x。” 注意“基数2”，即 我们认为是二分之一-您需要将2乘以多少才能得到512。

在二分查找算法中，每一步都将数组分为两部分。

我的加法。 即 在最坏的情况下，我们会进行尽可能多的操作，将数组分为两部分。 例如，我们可以将4个元素的数组分成两部分多少次？ 2次 还有8个元素的数组？ 3次 即 除法/运算数= log2（n）（其中n是数组中元素的数目）。

事实证明，操作数对输入元素数的依赖性描述为log2（n）


因此，使用Big O表示法，二进制搜索算法的复杂度为O（log n）。

将O（n ^ 2）提高到O（n log n）

让我们回到检查数组是否重复的任务。 我们遍历了数组的所有元素，并再次遍历了每个元素。 他们在O（n）内做O（n），即 O（n * n）或O（n ^ 2）。

我们可以用二进制搜索*代替嵌套循环。 即 我们只需要遍历O（n）的所有元素，在内部进行O（log n）。 结果是O（n * log n）或O（n log n）。

 const nums = [1, 2, 3, 4, 5]; const searchFor = function (items, num) { //use binary search! //if found, return the number. Otherwise... //return null. We'll do this in a later chapter. } const hasDuplicates = function (nums) { for (let num of nums) { //let's go through the list again and have a look //at all the other numbers so we can compare if (searchFor(nums, num)) { return true; } } //only arrive here if there are no dups return false; } 

*注意，以避免压印 。 使用二进制搜索来检查数组是否重复是一个不好的解决方案。 仅以Big O术语显示了如何评估上面代码清单中所示算法的复杂性。 对于本文而言，好的算法或不好的算法并不重要；可见性很重要。

用大O来思考

• 获得收集项的结果为O（1）。 无论是通过数组中的索引获取还是通过Big O表示法的字典中的键获取，都将为O（1）
• 对集合进行迭代为O（n）
• 同一集合上的嵌套循环为O（n ^ 2）
• 分而治之总是O（log n）
• 使用Divide和Conquer的迭代为O（n log n）