我记得前面部分的重要结论。 对于不包含多个信号的循环顺序行为(一个周期切换两次以上),每个信号的最小逻辑功能可以用以下形式表示(自然,在没有CSC冲突的情况下):
1)
其中a * b * ... * c是一个或多个变量的含义。 g + h + ... + i-这可能是一组由一个变量组成的空蕴涵。 x * f是2个变量的植入物,没有必要以最小形式存在。 除了x以外,所有变量都可以直接形式和反形式包括在公式中,这取决于相应事件的符号排列。 所有变量都仅在公式中作为参数包含一次。
在继续之前,我们将仔细研究一下分解等现象。 首先,分解是令人感兴趣的,它保留了自同步。 分解逻辑“非与”功能时,可以将其区分为一个新元素:
a)一个或多个牵连者,
b)一个植入物的多个信号(变量),
c)一台输入逆变器。
首先,我们考虑NOR AND函数的一种特殊情况。 所讨论模型的逻辑函数(x = a + b + c + d)的行为:
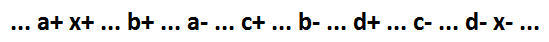
她可以将几个信号区分为一个单独的元素。
实际上,在分解过程中选择新元素就是添加新信号(f)。 为了维持正确的行为,半模块化和自同步,新添加的信号f的切换必须具有结果事件。 由于分解仅影响电路的一个元素(在这种情况下为x),并且不影响电路的其余元素,因此切换信号f仅会导致切换信号x。 否则,另一个信号的逻辑功能将取决于信号f。 鉴于此结论,让我们尝试突出显示除变量a以外的任何其他变量作为新元素f。 以变量b和c为例。 它们形成逻辑元素f = b + c。
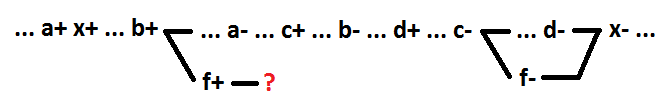
可以看出,对于f +事件,不可能在不违反行为正确性的情况下确定后果事件。 任何不包含变量a的信号组都不能在保持自同步的同时分配为单独的元素。
在此示例中,诸如a之类的信号将被称为开启。 在一般情况下,功能OR(与)的切换信号是信号,将其切换为1(0)会将功能的值从0更改为1(从1更改为0)。 为了在选择一个新元素时在逻辑功能“或”(AND)分解期间保持自同步,必须使用开关信号。 选择新元素时,还必须仅使用形成连接链的信号(在下面的示例中,a + b)。 x = f + c + d,f = a + b。
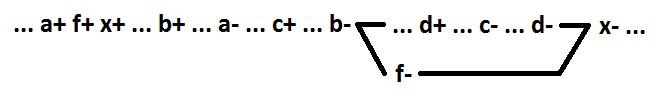
当使用a + b + d信号时,不会保留自同步。
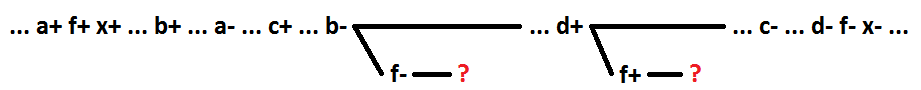
因此,对于逻辑函数OR(I)分解过程中没有多个信号的顺序行为,从包括信号在内的信号开始,突出显示信号部署过程中的前几个作为新元素,以确保电路是自同步的。
现在考虑非或函数(x =!A +!B)。 作为保持自同步的独立元素(f),我们只能选择与开关信号(x = f +!B,f =!A)对应的输入逆变器。 将其他输入逆变器分离为单独的元件将导致自同步的违反。
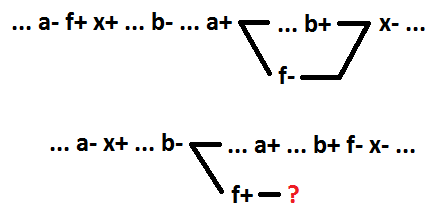
让我们继续进行AND-OR功能。 同样,作为“或”功能的开关信号,我们定义了“与”或功能的开关含义。 这是一个隐含的含义,将其值从0更改为1会导致函数的值从0更改为1。类似地,对于OR函数发现,对于分解逻辑AND-OR函数时没有多个信号的顺序行为,突出显示前几个在部署过程中,牵涉项从包含开始,保证了电路的自同步性得以保留。 否则,自同步将被破坏。 在下面的示例中,分解前x = a * b + c。 分解后,x = f + c,f = a * b。
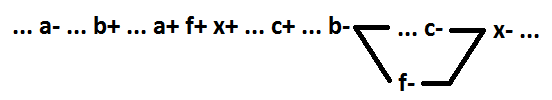
现在,对于AND-OR函数,我们将选择视为同一蕴含物中包含的多个变量的新元素。 仅考虑最小功能。 以下是函数示例x = a * b * c + d的所有可能选项(对于选项4-x = a * b * c + d + e,对于选项6-x = a * b * c * d + e) 。 高亮显示的元素是f = a * b。

在选项1中,切换分配的信号之一(a +)是x +事件的原因。 在选项2中,切换分配的信号(a-)之一是x-事件的原因。 在选项3和4中,分配的信号之一(分别为a +和a-)的切换位于事件x +和x-之间,而不是事件x-的原因。 选项5是选项4的特例,其中包含分配信号的含义。 剩余的选项6-分配信号的所有切换都位于事件x-和x +之间,而不是事件x +的原因。
如您所见,在选项1和6中,无法正确定位f事件。 这样的转换不是保留自同步的分解。 在选项2、3和4中,保持自同步。 但是,函数x的值却不同于f * c + d(4个选项的f * c + d + e)。 对于2个选项-x = f *(d + c),对于3个选项x = c * x + d *!F + x *!F,对于4个选项x =(f + d)*(e + c)。 这样的变换不是分解。
唯一的选择5是保留自同步的分解(x = f * c + d)。 在这种情况下,作为包含包含符中的一个单独元素,从包含开始选择前几个信号(包含隐含符And的信号与包含And功能的信号相同)。 但是,如上所示,分两步获得了相似的结果。 首先,突出了植入物的内含物。 在第二步中,从切换信号开始,在新元素中选择前几个信号。
让我们继续进行“非与”功能。 让我们将输入逆变器选为一个单独的元素。 信号a对应于元素x的输入,专用输入逆变器连接到该元素x(f =!A)。
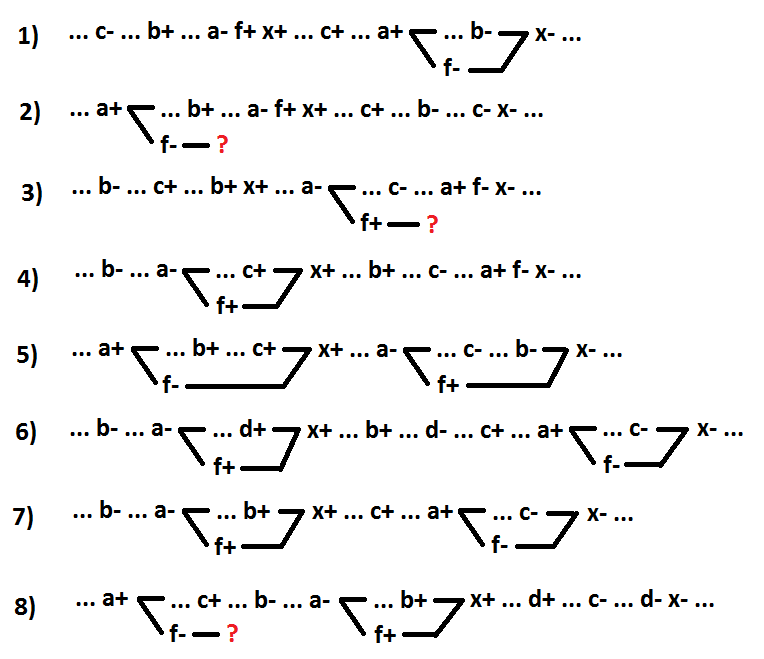
选项1和2-开关信号a是事件x +的原因(1-x =!A + b * c,2-x = b *!A + c)。 选项3和4-切换信号a是事件x-的原因(3-x =!A + b * c,4-x =!A * b + c)。 选项5和6-信号a的切换位于事件x +和x-之间,而不是事件x-的原因(5-x = b *!A + c,6-x =!A * b + d + c)。 选项7是选项6的特殊情况,其中信号a是包含相关信号(x =!A * b + c)的开关信号。 剩余的选项8-所有信号切换a都位于事件x-和x +之间,而不是事件x +的原因(x = c *!A * b + d)。
如您所见,选项2、3和8不能保留自同步,因为无法正确定位信号开关f。 对于选项4,转换后x = f *(c + b)。 对于选项5,转换后x = c *!F +!F * x + b * x。 对于选项6,转换后x =(f + c)*(d + b)。 这些转换(选项4、5和6)不是分解。 对于选项7,转换后x = f * b + c。 选项7是保留自同步的分解。 在这种情况下,与包括植入物的开关信号相对应的逆变器被分配为单独的元件。 使用上面的转换,在两个步骤中获得了相似的结果。 首先,突出显示包含的含义,然后将接通信号的输入反相器分配给它。 对于选项1,转换后x = f + b * c。 选项1也是保留自同步的分解。 这是选项7的特例,其中包含的牵连包含一个信号。
我们将获得的结果系统化。 对于所考虑的模型,在分解逻辑“非与”功能以保持自同步时,仅可能进行以下转换-将其分配为单独的元素:
1-一个或多个,从包含的重叠含义开始(特殊情况-从包含开始,对于几个重叠信号的非或选择功能);
2-在包含的暗示中,从包含开始,重叠信号;
3-对应于包含隐含信号的开关信号的输入反相器(特殊情况-对应于对应于开关信号的输入反相器的非或选择功能)。
如果不是在转换之前,则这些转换不允许隐含的包含。 因此得出这样的结论:如果逻辑函数包含一个包含多个信号且不包含在内的蕴含函数,则该函数不能使用保留自同步功能(最多两个输入元素)的分解来进行分段。 使用保留自同步的分解,可以将其中一个以上变量仅包含一个含蕴涵的任何非与或逻辑功能分解为两个输入元素(2I-NOT,2OR-NOT)。
步骤1-如果逻辑元素仅包含一个蕴含量(或所有蕴含量由一个变量组成),请转到步骤3,否则转到步骤2。
第2步-从包含开始,选择除一个以外的所有植入物作为单独的元素。 接下来,我们处理新收到的物品。 转到步骤1。
步骤3-如果元素包含两个变量,请转到步骤5,否则转到步骤4。
第4步-从包含开始,选择除一个以外的所有变量作为单独的元素。 接下来,我们处理新收到的物品。 转到步骤3。
步骤5-适用于所有接收到的两个输入元素。
步骤5.1-如果输入反相器都在两个输入上,我们将把元素转换为对偶。
步骤5.2-如果输入反相器为1,并且对应于未接通的信号,我们将把该单元转换为对偶单元。
步骤5.3-输入逆变器(如果有)突出显示为单独的元素。 粉碎完成。
现在回到文本开头的公式1。 如果蕴含项x * f不在逻辑表达式中,则该函数如下所示:x = a * b * c + g + h + i。 她的行为:
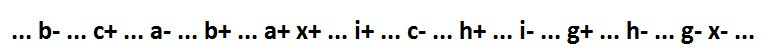
如您所见,多个变量(a * b * c)的唯一含义是包含性的。 借助分解功能,该功能可以分解为最少的组件,同时保持自同步。
如果蕴含式x * f存在于逻辑表达式中,则该函数如下所示:x = a * b * c + x * f + g + h + i。 她的行为:
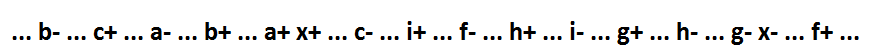
x * f的非包含性包含多个变量。 在保持自同步的同时,不能对此类功能进行分段。 但是我们应用了一种保留自同步的变换:将信号y-对偶添加到信号x。 加信号y仅改变信号x和信号的功能,信号的切换是事件x-的结果(变量x被变量y代替)。
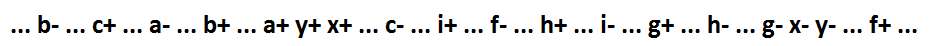
现在x =(f + i + h + g)* y,y = c * b * a + x。 函数f + i + h + g和c * b * a分别包括和x和y,它们可以分解为最小分量,同时保持自同步。
简化的行为模型(没有并行性,选择和多个信号)使您可以识别二进制过程中固有的属性。 在最小的基础上合成自同步电路是一种自然现象,不需要任何设计。