在上一篇文章中,我指出了在科学出版物中滥用t标准的问题有多普遍(这只能归因于其开放性,而且在任何课程,报告,培训任务等中使用时都会产生什么垃圾是未知的)。 。 为了讨论这一点,我讨论了方差分析的基础知识以及研究人员自己设定的显着性水平α。 但是,为了全面了解统计分析的整体情况,有必要强调一些重要的事情。 其中最基本的是错误的概念。
错误和不正确的应用程序:有什么区别?
任何物理系统都包含某种错误,不准确性。 以最多样化的形式出现:所谓的公差-相同类型的不同产品在尺寸上的差异; 非线性特性-当设备或方法根据严格已知的定律在一定范围内测量某物,然后变得不适用时; 离散性-在技术上我们无法确保平滑的输出特性时。
同时,这是纯粹的人为错误-设备,仪器和数学定律的错误使用。 系统固有的错误与应用此系统的错误之间存在根本差异。 重要的是要区分并且不要混淆这两个概念,它们被称为同一词“错误”。 在本文中,我更喜欢使用“错误”一词来表示系统的属性,而使用“错误使用”来代表系统的错误使用。
也就是说,标尺的误差等于设备的公差,从而在其画布上放置笔触。 在错误使用的意义上,错误是在测量手表细节时使用它。 杆秤的错误写在上面,重约50克,而杆秤的误用是在它上面重25公斤的袋子,这使弹簧从胡克定律的区域延伸到塑性变形的区域。 原子力显微镜的误差源于其离散性-您无法用比直径小于一个原子的探针“接触”物体。 但是,有许多方法可以滥用它或误解数据。 依此类推。
那么,这在统计方法上有什么样的错误呢? 而这个误差恰好是臭名昭著的显着水平α。
第一种和第二种错误
统计的数学工具中的一个错误是其贝叶斯概率本质本身。 在上一篇文章中,我已经提到了统计方法的基础:将显着性水平α确定为非法拒绝无效假设的最大可接受概率,然后由研究人员将这个值独立分配给研究人员。
您已经看到这个约定了吗? 实际上,在准则方法中没有熟悉的数学严谨性。 数学是根据概率特征运算的。
还有另一点是,在不同的上下文中可能会误解一个单词。 有必要区分概率的概念和事件的实际执行情况,以概率的分布表示。 例如,在开始我们的任何实验之前,我们都不知道结果将带来什么样的价值。 有两种可能的结果:使结果具有一定价值后,我们将真正获得或不获得它。 逻辑上两个事件的概率均为1/2。 但是前一篇文章中显示的高斯曲线显示
了我们正确猜测巧合
的概率分布 。
您可以通过示例清楚地说明这一点。 让我们掷两个骰子600次-常规和作弊。 我们得到以下结果:

在实验之前,对于两个立方体,任何面的损失都是相同的可能性-1/6。 但是,在实验之后,欺骗立方体的本质出现了,可以说六个落在其上的概率密度为90%。
化学家,物理学家和任何对量子效应感兴趣的人都知道的另一个例子是原子轨道。 从理论上讲,电子可以被“涂抹”在空间中并且几乎位于任何地方。 但实际上,在某些情况下,有90%或更多的情况会发生这种情况。 由具有90%的电子概率密度的表面形成的这些空间区域是球形,哑铃等形式的经典原子轨道。
因此,通过独立设置重要性级别,我们有意同意其名称中描述的错误。 因此,没有一个结果可以被认为是“完全可靠的”-我们的统计结论总是包含失败的可能性。
通过确定显着性水平α公式化的
错误称为
第一类错误 。 可以将其定义为“错误警报”,或更准确地说,是误报结果。 实际上,“错误地拒绝原假设”是什么意思? 这意味着错误地将观察到的数据用于两组之间的显着差异。 为了对疾病的存在做出错误的诊断,急于向世人揭示一个实际上不存在的新发现-这些都是第一类错误的例子。
但是,那是否会有假阴性结果呢? 完全正确,它们被称为
第二种错误 。 实例是该研究导致的不合时宜的诊断或令人失望的结果,尽管实际上它包含重要的数据。 第二种错误由字母β表示,这很奇怪。 但是这个概念本身对统计的重要性不如1-β。 数字1-β称为
标准的
幂 ,正如您可能猜到的,它表示标准不遗漏重要事件的能力。
但是,第一类和第二类错误的统计方法的内容不仅限于它们。 这些错误的概念可以直接用于统计分析。 怎么了
ROC分析
ROC分析(根据接收器的工作特性)是一种用于量化特定属性对对象的二进制分类的适用性的方法。 简而言之,我们可以提出一些方法来区分生病的人和健康的人,猫的狗,黑的人和白人,然后检查该方法的有效性。 让我们再来看一个例子。
让您成为一名崭新的法医科学家,并开发一种谨慎谨慎地确定一个人是否为罪犯的新方法。 您想出了一个定量的信号:通过人们听Mikhail Krug的频率来评估人们的犯罪倾向。 但是,您的症状会产生足够的结果吗? 让我们做对。
您将需要两组人来验证您的条件:普通公民和罪犯。 的确,让我们假设他们听Mikhail Krug的平均年度时间有所不同(见图):
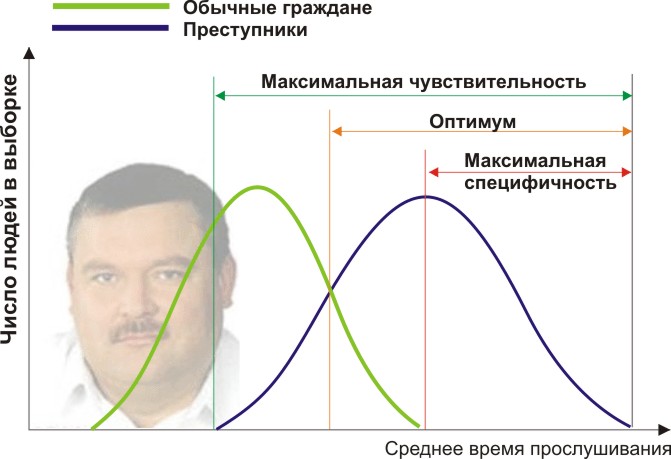
在这里,我们可以看到,通过收听时间的定量信号,我们的样本相交。 有人在广播中自发地听广播而不犯罪,有人通过听其他音乐甚至失聪来违法。 我们有什么边界条件? ROC分析引入了选择性(敏感性)和特异性的概念。 敏感性定义为能够识别我们所有关注点的能力(在此示例中为罪犯),并且具有特异性-不会捕获任何假阳性(不会使普通居民受到怀疑)。 我们可以设置一些关键的定量特征,将某些特征与其他特征分开(橙色),范围从最大灵敏度(绿色)到最大特异性(红色)。
让我们看下图:

通过移动属性的值,可以更改假阳性和假阴性结果的比率(曲线下的面积)。 以同样的方式,我们可以定义灵敏度=位置。 Res-t /(阳性Res-t +假阴性。Res-t),特异性=阴性。 Res-t /(负Res-t +假阳性。Res-t)。
但最重要的是,我们可以在定量属性值的整个范围内评估阳性结果与假阳性结果的比率,这就是我们所需的ROC曲线(见图):

以及我们如何从该图了解我们的属性有多好? 很简单,计算曲线下的面积(AUC,曲线下的面积)。 虚线(0,0; 1,1)表示两个样本的完全重合和完全没有意义的标准(曲线下的面积为整个正方形的0.5)。 但是,ROC曲线的凸度仅表示准则的完善。 如果我们设法找到样本完全不相交的标准,则曲线下方的区域将占据整个图形。 通常,该特征被认为是良好的,如果AUC> 0.75-0.8,则可以使一个样本与另一个样本可靠地分离。
通过此分析,您可以解决各种问题。 由于迈克尔·克鲁格(Michael Krug)认定有太多家庭主妇受到怀疑,此外,错过了听Noggano的危险累犯,您可以拒绝此标准并制定另一个标准。
ROC分析已成为处理无线电信号并在遭受珍珠港袭击后识别“敌还是友”的一种方法(因此对接收器特性起了陌生的称呼),已广泛应用于生物医学统计中,以进行生物标志物面板的分析,验证,创建和表征等 如果它基于声音逻辑,则可以灵活使用。 例如,您可以通过采用高度特定的标准,提高检测心脏病的效率并且不使不必要的患者负担过多的医生来为退休的核心患者制定医学检查的适应症。 相反,在以前未知病毒的危险流行中,您可以提出一个高度选择性的标准,以便没有其他人从字面上逃过疫苗接种。
在验证标准的描述中,我们遇到了两种错误及其可见性。 现在,从这些逻辑基础出发,我们可以销毁一系列对结果的错误刻板印象。 一些不正确的表述吸引了我们的思想,常常被它们相似的词语和概念所迷惑,并且还因为很少注意错误的解释。 也许这需要单独编写。