扫线法Delaunay三角剖分算法

美好的一天！

在本文中，我将详细描述由于使用“扫描直线”思想在平面上构造Delaunay三角剖分而获得的算法。 当我阅读有关三角测量的文章时，其中有很多想法从未见过。
也许有人也会发现它们不寻常。 我将尝试按照最佳传统做所有事情，并在故事中包括以下内容：对使用的数据结构的描述，算法步骤的描述，正确性证明，时间估计以及与使用kD树的迭代算法的比较。

问题的定义和陈述

三角剖分

他们说，如果通过边连接几对点，则在平面上的点集上指定了三角剖分，结果图形中的任何有限面都形成三角形，边不相交，并且图的边数最大。

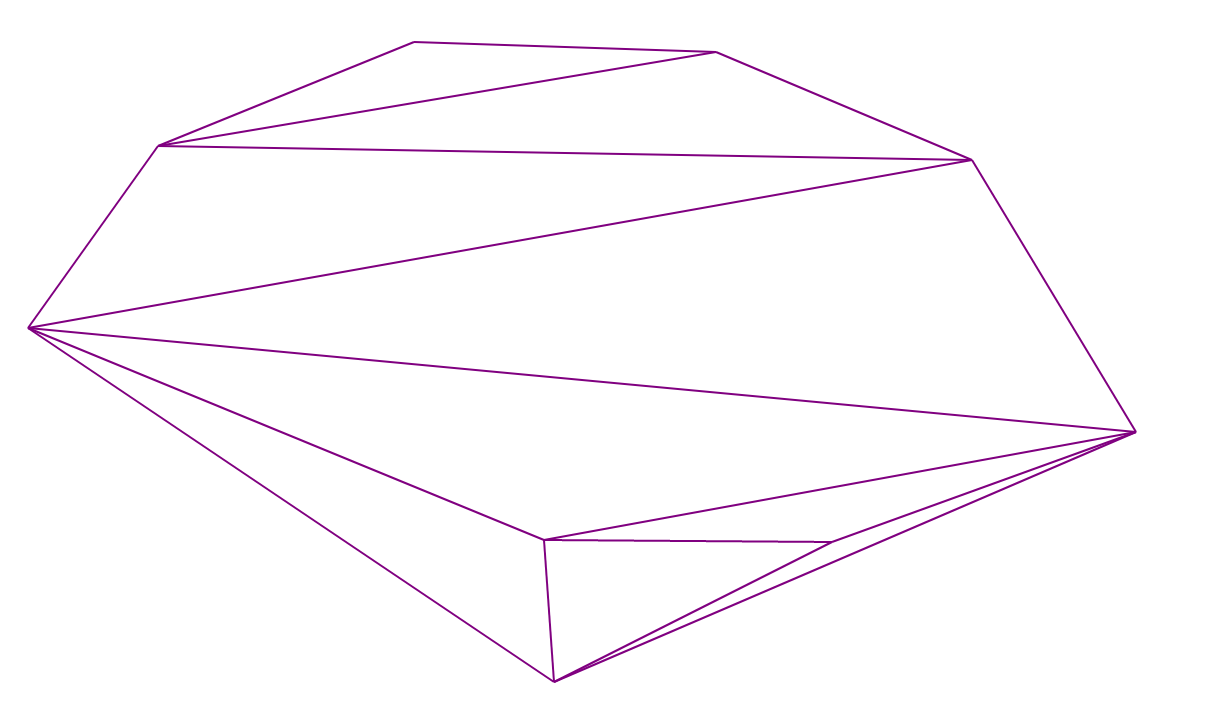
德劳内三角剖分

Delaunay三角剖分是一种三角剖分，其中对于任何三角形来说，围绕它的外接圆内的原始设置中确实没有任何点是正确的。

注意 ：对于一组给定的点，其中在同一圆上没有4个点，则仅存在一个Delaunay三角剖分。

德劳内条件

让我们对点集进行三角剖分。 我们说如果某个点的子集满足Delaunay条件，则该子集上的三角剖分是他的Delaunay三角剖分。

Delaunay三角剖分准则

对于在三角剖分中形成四边形的所有点，满足Delaunay条件的情况等同于该三角剖分是Delaunay三角剖分的事实。

注意 ：对于非凸四边形，始终满足Delaunay条件，而对于凸四边形（其顶点不在同一圆上），恰好有2个可能的三角剖分（其中一个是Delaunay三角剖分）。

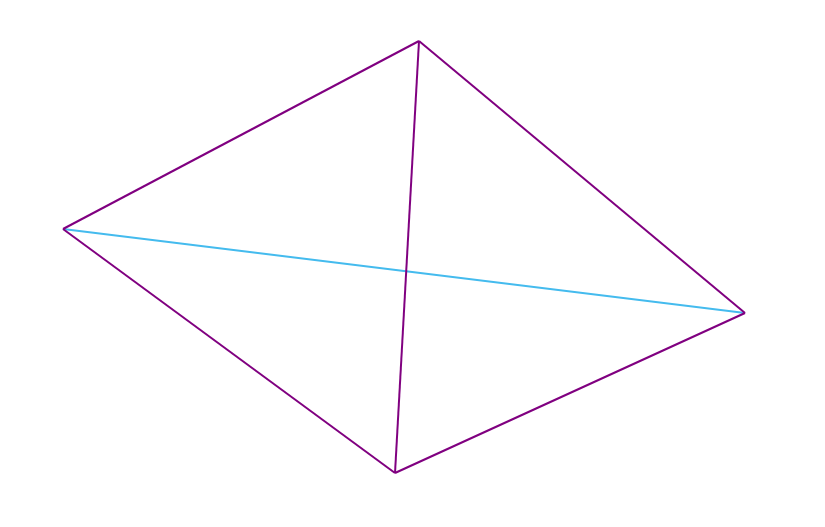
任务是为给定的点集构造Delaunay三角剖分。

算法说明

可见点和可见边缘

让最小凸包（以下称为MBO）具有有限的一组点（连接某些点的边，以便它们形成包含该组所有点的多边形）和位于包壳外部的点A。 如果将平面连接到点A的线段不与MBO相交，则将点A称为可见点。

如果MBO边缘的端点对于A可见，则称为MBO边缘。

在下图中，红点可见的边缘用红色标记：

注意 ：Delaunay三角剖分轮廓是建立点的MBO。

备注2 ：在算法中，添加的点A可见的边形成一条链，即，一行中有多个MBO边

将三角剖分存储在内存中

Skvortsov [1]一书中很好地描述了一些标准方法。 由于算法的特殊性，我将提供自己的版本。 由于我们要检查Delaunay条件的4边形，因此考虑它们的结构。 三角剖分中的每个四边形是2个具有共同边的三角形。 每条边均具有与其相邻的2个三角形。 因此，三角剖分中的每个四边形都是由一个边和与相邻三角形中与该边相对的两个顶点生成的。
由于沿着边缘和两个顶点恢复了两个三角形及其邻接，因此我们可以为所有此类结构恢复三角剖分。 因此，提出了将具有两个顶点的边缘存储在集合中并沿着该边缘（有序的一对顶点）执行搜索。

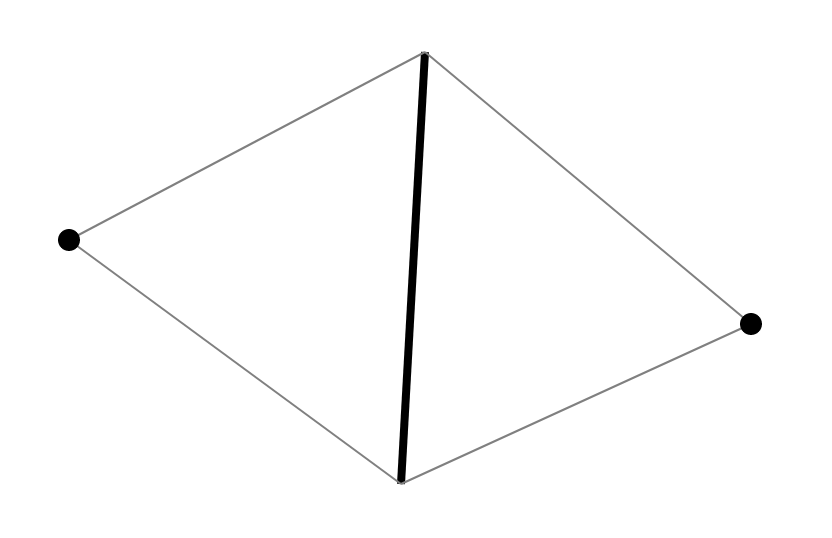
演算法

扫掠线的思想是将所有点沿一个方向排序，然后依次处理。

1. 沿直线对所有点排序（为简单起见，按坐标 $$$x$）
2. 我们在前三个点上构造一个三角形。
   
   此外，对于每个下一个点，我们将执行以下步骤，以保持不变：已添加的点存在Delaunay三角剖分，因此，对其进行MBO。
3. 添加由可见边缘和点本身形成的三角形（即，将所讨论点的边缘添加到可见边缘的所有末端）。
4. 我们在Delaunay条件下检查可见边缘生成的所有四边形。 如果在某处未满足该条件，则我们在四边形中重建三角剖分（我记得其中只有两个）并递归运行当前四边形的边生成的四边形的检查（因为只有在它们之后才可能违反Delaunay条件）。

注意 ：在递归开始过程中的步骤（4）中，您无法检查由在此迭代中考虑的点产生的边所生成的四边形（总是有四个中的两个）。 大多数情况下，它们将是非凸的，因为凸的证明是纯几何的，我将其留给读者。 此外，我们假设每次重建仅执行2次递归启动。

验证Delaunay条件

在同一本书中可以找到测试Delaunay条件的四边形的方法[1]。 我只注意到，当从那里选择具有三角函数的方法时，如果实现不正确，则可以得到正弦的负值，将它们取模是有意义的。

搜索可见边缘

有待了解如何有效地找到可见的边缘。 请注意，先前添加的点S在当前迭代中位于MBO中，因为它具有最大的坐标 $$$x$，并且在当前点也可见。 然后，注意到可见边缘的末端形成了可见点的连续链，我们可以沿着MBO在两个方向上从点S出发，并在可见时收集边缘（使用向量积检查边缘的可见性）。 因此，将MBO存储为双重连接的列表很方便，在每次迭代中都删除可见边缘并从考虑的点添加2个新边缘。

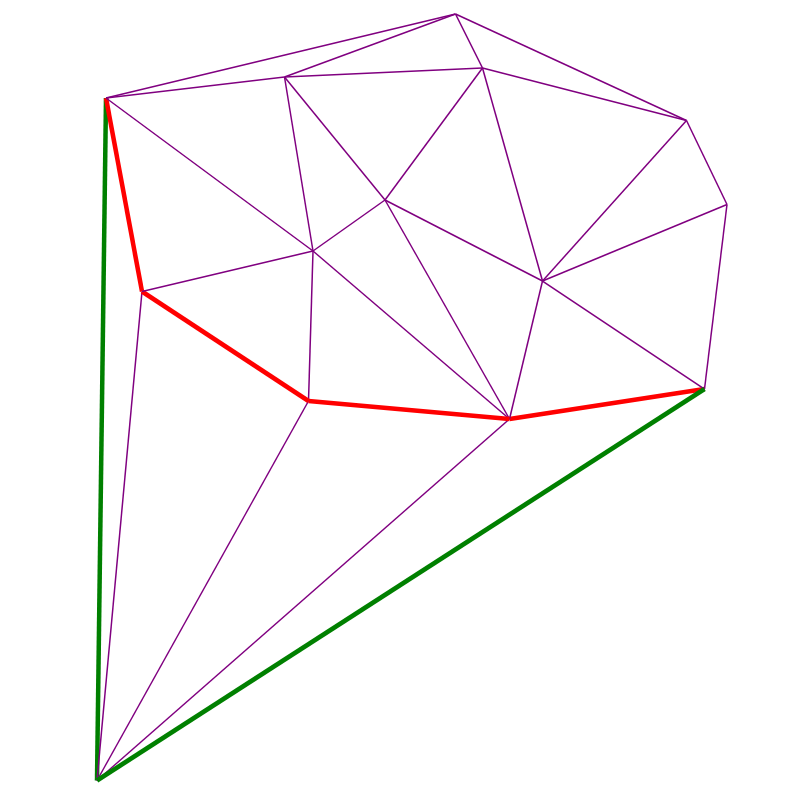
算法可视化

两个红点-已添加和在前。 时刻的红色边缘构成步骤（4）中的递归堆栈：

算法正确性

为了证明算法的正确性，足以证明步骤（3）和（4）中不变量的守恒。

步骤（3）

显然，在步骤（3）之后，我们对当前点集进行了三角剖分。

步骤（4）

在步骤（4）的过程中，所有不满足Delaunay条件的四边形都在递归堆栈中（根据说明进行），这意味着在步骤（4）的末尾，所有四边形都满足Delaunay条件，即实际上构造了Delaunay三角剖分。 然后剩下的就是证明步骤（4）中的过程总有一天会结束。 这是由于以下事实：在重建过程中添加的所有边都来自所讨论的当前顶点（即 $$$k$不超过 $$$k-1$），并且在添加这些边后，我们将不再考虑由它们生成的四边形（请参见前面的说明），这意味着我们将添加不超过一次。

时间复杂度

平均而言，该算法在均匀的正态分布上效果很好（结果显示在下表中）。 假设其工作时间为 $$$O（NlogN）$。 最坏的情况是进行评估 $$$O（N ^ 2）$。

让我们看一下各部分的工作时间，了解哪个对总时间有最大的影响：

按方向排序

为了进行排序，我们将使用估计值 $$$O（NlogN）$。

搜索可见边缘

首先，我们证明搜索可见边缘所花费的总时间为 $$$O（N）$。 请注意，在每次迭代中，我们发现所有可见边缘以及线性时间内的另外2个（第一次不可见）。 在步骤（3）中，我们向MBO添加新的2条边。 因此，总计不超过 $$$2N$因此，各种可见的肋骨将不再存在 $$$2N$。 我们还会发现 $$$2N$不可见的边缘。 因此，总而言之 $$$4N$对应时间的肋骨 $$$O（N）$。

建立新的三角形

从步骤（3）构造具有已知边缘的三角形的总时间显然是 $$$O（N）$。

重建三角剖分

剩下要处理步骤（4）。 首先，请注意，检查Delaunay条件并进行重建（如果未满足）是非常昂贵的操作（尽管它们适用于 $$$O（1）$） 仅在检查Delaunay条件时，才能执行约28个算术运算。 让我们看一下此步骤中的平均重建次数。 下面给出了一些分布的实际结果。 对于他们，我真的想说平均重排数以对数速度增长，但让我们将此作为假设。

在这里，我还想指出，每个点的平均重排数量可能与执行排序的方向有很大不同。 因此，对于长宽比为100000：1的长百万个矩形上均匀分布的一百万，此数字在1.2到24之间变化（这些值分别在对数据进行水平和垂直排序时获得）。 因此，我看到了以任意方式选择排序方向的要点（在此示例中，通过任意选择，平均可以获得大约2次重建），或者如果事先知道数据，则手动选择它。

因此，程序通常将主要时间带到步骤（4）。 如果运行很快，则考虑加快排序是有意义的。

最坏的情况

最坏的情况 $$$k$第迭代发生 $$$k-1$步骤（4）中的递归调用，即对所有i求和，我们得到最坏情况下的渐近行为 $$$O（N ^ 2）$。 下图显示了一个可以长时间运行程序的漂亮示例（添加输入10,000点的新点时，平均重建1100个）。

与使用kD树构造Delaunay三角剖分的迭代算法的比较

迭代算法的描述

我将简要描述上述算法。 当下一个点到达时，我们使用kD树（如果您不知道，我建议您在某处阅读），我们发现一个已经非常接近它的三角形。 然后绕过深度，我们寻找一个三角形，点本身掉入其中。 我们将边缘扩展到找到的三角形的顶点，并针对新的四边形实际执行算法中的步骤（4）。 由于该点可以在三角剖分之外，为简化起见，建议使用大三角形覆盖所有点（预先构建），这将解决该问题。

算法的相似性

实际上，如果按方向将点按顺序添加，则我们的算法实际上与迭代的工作原理相同，只不过重排的次数较少。 以下动画完美地展示了这一点。 在其上，从右到左添加了点，它们全部被一个大三角形覆盖，随后将其删除。

算法差异

在迭代算法中，点的定位（搜索所需三角形）平均发生在 $$$O（logN）$，在上述分布上，在任意顺序的积分供应条件下，平均会发生3次重排（如[1]所示）。 因此，扫描线在本地化中赢得了迭代算法的时间，但在重建中却失去了它（我记得这是非常困难的）。 另外，迭代算法在线运行，这也是它的显着特征。

结论

在这里，我仅展示了算法运算产生的一些有趣的三角剖分。

美丽的图案

正态分布，1000点

平均分配1000点

建立在俄罗斯所有城市位置的三角剖分

在这里，您可以看到我的算法示例代码：
github.com/Vemmy124/Delaunay-Triangulation-Algorithm

感谢您的关注！

文学作品

[1] Skvortsov A.V. Delaunay三角剖分及其应用。 汤姆斯克：汤姆出版社。 大学，2002.-128羽 书号5-7511-1501-5