迷宫：分类，生成，寻找解决方案

这篇经典文章详细介绍了创建和经历迷宫的最流行方法。 本文分为四个部分：分类，生成算法，求解迷宫的算法和其他使用迷宫的操作。

迷宫分类

迷宫整体（以及由此产生的迷宫）可以分为七个不同的类别：维，超维，拓扑，细分，路由，纹理和优先级。 迷宫可以任意组合使用每个类别中的一个元素。
尺寸：尺寸类实质上决定了迷宫填充的空间尺寸。 可以使用以下类型：

• 
  
  二维 ：大多数迷宫式迷宫，无论是纸制的还是真实的，都具有这个尺寸，也就是说，我们总是可以在一张纸上显示迷宫式的平面图，然后沿着迷宫式平面移动，而不会越过迷宫的任何其他通道。
• 三维 ：三维迷宫具有多个层次； 在其中（至少在正交形式中），除了四个基本方向之外，通道还可以上下移动。 3D迷宫通常可视化为带有上下楼梯的2D水平阵列。
• 
  
  高维 ：您可以创建四维迷宫，甚至可以创建多维迷宫。 有时，它们被可视化为3D迷宫，其中“门户”贯穿第四个维度，例如，“过去”和“未来”的门户。
• 
  
  交织 ：具有交织的迷宫-本质上是二维（或更确切地说是2.5维）迷宫，但是通道之间可以相互重叠。 在显示时，通常很明显的是死角在哪里，一个通道在另一个通道的上方。 真实世界中的迷宫部分交错，其中有连接迷宫的一部分和另一部分的桥梁。

超尺寸：根据超尺寸进行分类对应于穿过迷宫的物体的尺寸，而不是迷宫本身。 可以使用以下类型：

• 
  
  非迷宫：几乎所有的迷宫，即使是高维或有特殊规则的迷宫，通常都是非迷宫。 在它们中，我们使用一个点或一个小物体（例如，一个球或一个球员本人）从一个点移动到另一个点，铺砌的路线形成一条线。 在每个点上，都有很容易计数的选择。
• 超级迷宫：超级迷宫是迷宫，其中要解决的对象不仅仅是一点。 标准的超级迷宫（或一阶超级迷宫）由沿路径移动时形成表面的线组成。 超级迷宫只能存在于3D或更大尺寸的介质中，超级迷宫的入口通常不是点，而是一条线。 超级迷宫本质上是不同的，因为必须考虑并同时处理沿线的几个部分，并且在任何给定的时间，对于沿线进行的操作，几乎有无数的状态和选项。 解线是无限的，或者其端点在超迷宫之外，以避免将线压缩到一点，因为在这种情况下，它可以被认为是非超迷宫。
• 超级迷宫：超级迷宫可以是任意高维度。 超超迷宫（或二级超迷宫）再次增加了所求解对象的尺寸。 在此，要解决的目标是一个平面，该平面在沿着路径移动时会形成三维图形。 超级迷宫只能存在于4D或更高维度的环境中。

拓扑：拓扑类描述了迷宫空间作为整体存在的几何形状。 可以使用以下类型：

• 
  
  普通 ：这是欧几里得空间中的标准迷宫。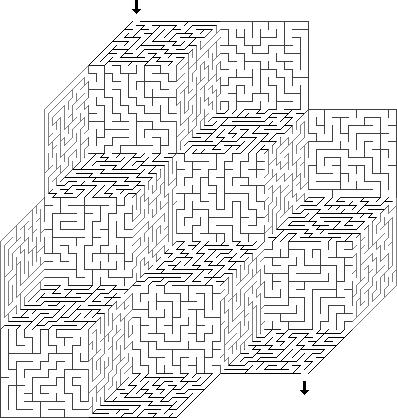
• 
  
  Planair ：术语“ planair”描述具有异常拓扑结构的任何迷宫。 通常，这意味着迷宫的边缘以有趣的方式连接。 示例：立方体表面上的迷宫，莫比乌斯带的表面上的迷宫和等效于左右两边成对连接的圆环上的迷宫。

棋盘格化：构成迷宫的各个单元的几何形状的分类。 现有类型：

• 
  
  正交 ：这是标准的矩形网格，其中的单元格具有直角相交的通道。 在镶嵌细分的情况下，它们也可以称为伽马迷宫。
• 
  
  三角洲 ：三角洲迷宫由相连的三角形组成，每个单元格最多可以连接三个通道。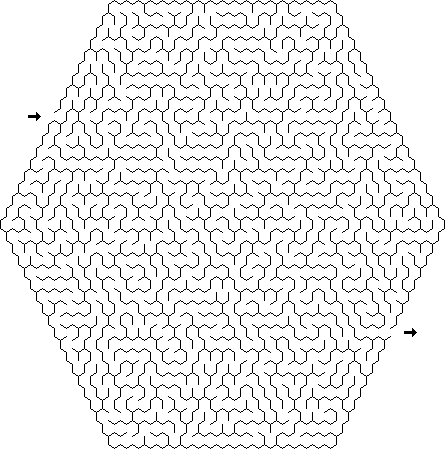
• 
  
  Sigma ：迷宫由相连的六边形组成； 每个单元最多可以有六次通过。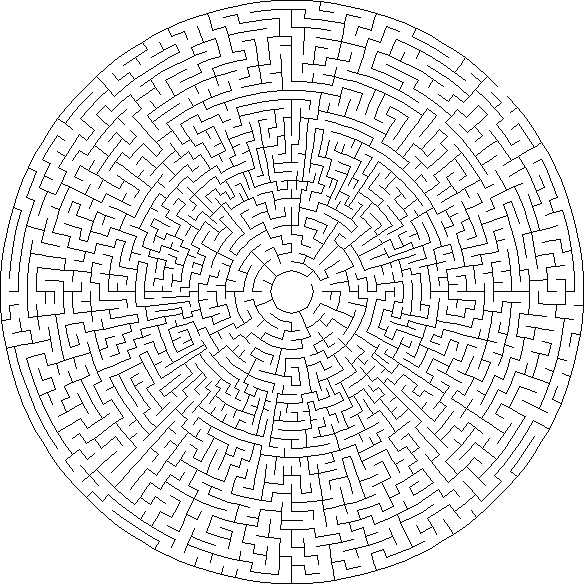
• 
  
  Theta ： Theta迷宫由通道的同心圆组成，其中起点或终点在中心，另一个在外边缘。 单元通常具有四个可能的连接路径，但由于通道外环中单元数量的增加，可能会有更多的连接路径。
• 
  
  Epsilon ： Epsilon迷宫由相连的八边形或正方形组成，其中每个单元最多可以经过八或四遍。
• 
  
  Zeta ： Zeta迷宫位于矩形网格上，除了水平和垂直通道外，对角通道均允许成45度角。
• 
  
  欧米茄（Omega） ：术语欧米茄（Omega）几乎是指具有恒定非正交镶嵌效果的所有迷宫。 Delta，sigma，theta和ipsilon迷宫属于这种类型，就像您可以想到的许多其他方案一样，例如，由成对的直角三角形组成的迷宫。
• 
  
  裂纹 ：裂纹迷宫是无定形细分的无定形迷宫，其中的墙壁和走道以任意角度放置。
• 
  
  分形 ：分形迷宫是由较小的迷宫组成的迷宫。 来自嵌套细胞的分形迷宫是在放置其他迷宫的每个单元中的迷宫，此过程可以重复多次。 无限递归分形迷宫是一个真实的分形，迷宫中的内容会自我复制，从而创建一个无限大的迷宫。

路由：按路由分类可能是生成迷宫中最有趣的方面。 “发件人”与上述类别中定义的几何图形中的通过类型相关联。

• 
  
  理想 ： “理想”是没有回路或闭合回路且没有不可触及区域的迷宫。 它也被称为简单连接迷宫。 从每个点到任何其他点都只有一条路径。 迷宫只有一种解决方案。 从编程的角度来看，这样的迷宫可以描述为树，单元或顶点的连接集。
• 
  
  编织 ：编织意味着迷宫中没有死角。 它也被称为纯多重连接迷宫迷宫。 在这样的迷宫中，使用了彼此闭合并返回的通道（因此称为“柳条”），它们使他们花更多的时间绕圈行走而不是陷入死胡同。 高质量的编织迷宫比相同大小的理想迷宫要复杂得多。
• 
  
  单路径（Unicursal） ：单路径表示没有叉子的迷宫。 单向迷宫包含一个较长的缠绕通道，该通道会在整个迷宫中改变方向。 仅当您不小心中途退回并且不返回起点时，这不是很复杂。
• 
  
  稀疏：稀疏的迷宫不会通过每个像元，也就是说，其中一些没有创建。 这意味着存在无法到达的区域，从某种意义上说，这是柳条迷宫的对立面。 添加墙时可以应用类似的概念，因此您可以在宽阔的过道和房间中获得不平坦的迷宫。
• 部分柳条：部分柳条迷宫是一个混合的迷宫，既有环又有死角。 “柳条”一词可用于定量评估，即，“编织性强的迷宫”是指去除了许多环或壁的迷宫，而“编织性较弱的迷宫”中只有少数。

纹理：纹理分类描述具有不同工艺路线和几何形状的通道的样式。 纹理不仅是可以打开或关闭的参数。 以下是一些变量示例：

• 
  
  偏见 ：在迷宫中，通道错位，笔直的通道在一个方向上的传播比在其他方向上的传播更多。 例如，在水平位移较大的迷宫中，我们从左到右会有很长的通道，而从上到下只有很短的通道将它们连接起来。 这样的迷宫通常更难以通过纤维。
• 
  
  飞越 ：“ 飞越”度量标准确定在出现强制转弯之前，过道将花费多长时间。 在低跨度的迷宫中，没有直道会超过三个或四个单元，并且看起来非常随机。 在高跨度的迷宫中，迷宫将具有很大比例的长程通过，这将使其看起来像微芯片。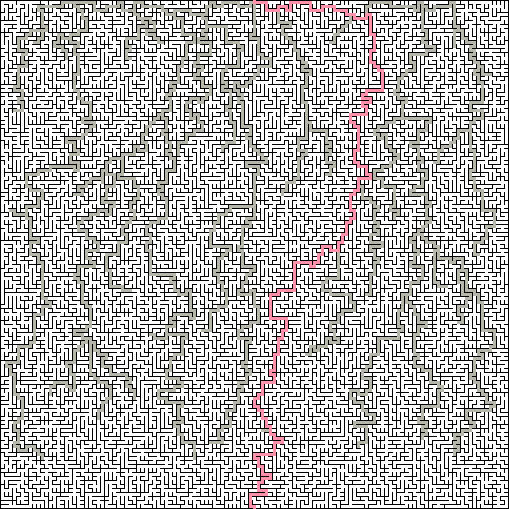
• 
  
  精英：迷宫的 “ 精英 ”指标决定了溶液的长度相对于迷宫的大小。 精英迷宫通常有一个简短而直接的解决方案，而在非精英迷宫中，该解决方案会经过迷宫的大部分区域。 高质量的精英迷宫比非精英迷宫要复杂得多。
• 
  
  对称 ：对称的迷宫具有对称的通道，例如，相对于中心旋转对称，或沿水平或垂直轴反射。 迷宫可以是部分或完全对称的，并且可以重复多次。
• 
  
  同质性：同质算法以相等的概率生成所有可能的迷宫。 如果迷宫看起来像是由均质算法生成的典型迷宫，则可以将其称为具有均质纹理。 理论上，异构算法还可以在任何空间中生成所有可能的迷宫，但概率不相等。 异质性可能会进一步发展-可能会有迷宫算法永远不会产生。
• 河流流动： “流动”特性意味着在创建迷宫时，该算法将寻找并清洁相邻单元（或壁）到当前的单元（或壁），也就是说，它将流入（因此称为“流动性”）迷宫中仍未创建的部分，例如水。 在流速较低的理想迷宫中，通常会有许多短死角，而在“流体”迷宫中，死角较少，但死角会更长。

优先：这种分类表明，创建迷宫的过程可以分为两种主要类型：添加墙壁和雕刻通道。 通常，在生成此代码时，它仅归因于算法上的差异，而不是迷宫中的明显差异，但是将其考虑在内仍然很有用。 经常以两种方式生成相同的迷宫：

• 添加墙：优先考虑墙的算法始于空白区域（或外部边界），并在此过程中添加墙。 在现实世界中，由树篱，天花板或木墙组成的真正迷宫无疑是增加了墙壁。
• 切割通道：优先处理通道的算法从实体块开始，并在此过程中剪切通道。 在现实世界中，此类迷宫是矿井隧道或管道内的迷宫。
• 
  
  模板：迷宫当然可以同时切割通道并增加墙壁； 一些计算机算法可以做到这一点。 迷宫模板是不是迷宫的图形图像，它在最少的步骤中变成了真正的迷宫，但仍然保留了原始图形模板的纹理。 复杂的迷宫样式（例如相交的螺旋）更易于在计算机中实现为模式，而不是在保留样式的同时尝试创建正确的迷宫。

其他：以上内容绝不是详尽列出所有可能的类或每个类中的元素。 这些只是我自己创建的迷宫类型。 请注意，几乎所有类型的迷宫，包括具有特殊规则的迷宫，都可以表示为有向图，其中每个状态中将存在有限数量的状态和有限数量的选择，这称为迷宫等效性 。 这里是迷宫的其他一些分类和类型：

• 
  
  方向 ：在某些段落上，您只能沿一个方向移动。 从编程的角度来看，与描述所有其他类型的无向图相反，这种迷宫将由有向图描述。
• 
  
  分割 ：迷宫可以具有对应于不同类别的不同部分。
• 
  
  无限长的迷宫：我们可以创建无限长的迷宫（有限数量的列和任意数量的行），但同时仅将迷宫的一部分存储在内存中，从一端“滚动”到另一端，并在创建下一行时破坏前一行。 一个示例是“搜索和杀死”算法的修改版本。 可以想象一个由单个框架组成的长片形式的潜在迷宫。 一次仅两个连续的帧被存储在存储器中。 让我们运行“搜索并杀死”算法，尽管它会产生容易出现在顶部帧的偏差，所以它首先结束。 完成后，不再需要该框架，您可以打印它或对其进行其他操作。 尽可能将其丢弃，将部分创建的下部框架设为新的上部框架，然后清除新的下部框架。 重复该过程，直到我们决定停止为止，然后等到“狩猎与杀死”完成两个帧。 唯一的限制是，迷宫永远不会有一条路径朝入口分支超过两帧。 创建无尽迷宫的最简单方法是Eller算法或Sidewinder算法，因为它们已经一次创建了一行迷宫，因此您可以让它们无休止地向迷宫添加行。
• 
  
  虚拟分形迷宫：虚拟是一种迷宫，其中整个迷宫没有同时存储在内存中。 例如，在您穿过大型迷宫的模拟中，它只能存储您所在位置附近的部分100x100通道。 嵌套分形迷宫的扩展可用于创建巨大的虚拟迷宫，例如每十亿次通过十亿次。 如果我们建立每十亿次通行的迷宫的真实副本（通道之间的距离为六英尺），那么它将充满地球6000多次！ 考虑一个10 ⁹到10 ⁹通过的迷宫，或一个只有9个等级的封闭迷宫。 如果我们希望周围至少有一个100x100的零件，那么我们就可以在最低级别创建一个100x100的子迷宫通行证，并在其中嵌入七个10x10的迷宫，以便准确知道墙在100x100零件中的位置。 （实际上，最好有四个相邻的部分，尺寸为100x100，如果您靠近该部分的边缘或拐角，则形成一个正方形，但此处适用相同的概念。）为确保迷宫在移动时保持不变且不变，我们有一个公式，在每个嵌套级别为每个坐标定义一个随机种子数。 虚拟分形迷宫类似于Mandelbrot分形，在其图像中虚拟存在，我们需要以相当高的放大倍数访问某个坐标。 以便它出现。

迷宫算法

这是创建上述各种迷宫类的通用算法的列表：

• 
  
  理想 ：创建一个标准的理想迷宫，通常必须对其进行“生长”，以确保没有环和孤立区域。 我们从外墙开始，随机添加与之接触的墙的片段。 我们继续在迷宫中随机添加墙段，但要确保每个新段都从现有墙的一端开始触碰，而另一端在迷宫中仍未创建的部分。 如果添加墙段，其两端与迷宫的其余部分分开，则这将创建一个未连接的墙，并在其周围形成一个环;如果添加墙段，其两端都接触迷宫，则将创建一个无法触及的区域。 这是增加墙壁的一种方法。 它几乎类似于切出通道，在通道中，通道的一部分被切开，因此只有一端接触现有通道。
• 
  
  : , , . : (1) , (2) , , -«», (3) , , , (4) , , (3) , , .
• 
  
  : — , , , , . U- , , , , . . , : , , , . , . , .
• 
  
  : , . , , . - , , , , .
• 3D : , , , . - .
• 
  
  : , , . ( ): , , , . , . , ; , . , , .
• 
  
  Crack : Crack- , , . , , , «» . , , . , - . , , ; . , .
• 
  
  : «» , , . , - : (1) , . (2) , , , , , (.. ). (3) , , . , .
• 
  
  : — 3D-, -, , . 3D- , , . , , . , . , ( ), , , .
• 
  
  Planair : Planair- , . — . , .
• 
  
  : , , , -, , , , . , . , , , , , .

创建完美迷宫的方法有很多，每种都有自己的特点。以下是特定算法的列表。所有这些都描述了通过切除通道来创建迷宫的方法，但是，除非另有说明，否则每种方法都可以通过添加墙来实现：

• 
  
  递归回溯器 ： - recursive backtracker, , . , , . , , . , . , . , , , . , . Recursive backtracking , , , .
• 
  
  : , . , «» , , . , , ( ). , . , , . , - , , . , , . , . , - (union-find algorithm): , . . , - .
• 
  
  Prim的算法（true） ：该算法通过处理唯一的随机边缘权重来创建最小的生成树。 所需的内存量与迷宫的大小成正比。 我们从任何顶点开始（无论从顶部开始，完成的迷宫都是一样的）。 我们选择具有最小重量的通道边缘，以将迷宫连接到尚不存在的点，然后将其连接到迷宫。 当所讨论的边缘不再留下时，迷宫完成。 为了有效地选择下一条边缘，您需要一个优先级队列（通常使用堆来实现），该队列存储边框的所有边缘。 但是，此算法相当慢，因为从堆中选择项目需要花费log（n）时间。 因此，最好还是选择Kraskal算法，因为它更快并且创建具有相同结构的迷宫，它也可以创建最小的生成树。 实际上，使用相同的随机种子，Prima和Kraskal算法可以创建相同的迷宫。
• 
  
  Prim的算法（简化） ：此Prim的算法创建最小的生成树。 这样简化以使边缘的所有权重都相同。 它需要与迷宫大小成比例的存储容量。 我们从一个随机峰开始。 我们随机选择连接迷宫的通道边缘和尚不存在的点，然后将其连接到迷宫。 当所讨论的边缘不再留下时，迷宫完成。 由于边缘没有权重并且没有排序，因此可以将它们存储为简单列表，也就是说，从列表中选择元素将非常快且花费固定时间。 因此，它比具有随机边缘权重的真正Prim算法要快得多。 与真正的Prima算法相比，创建的迷宫纹理将具有较低的屈服指数和更简单的解决方案，因为它像溢出的糖浆一样从起点均匀分布，并且不会绕过重量较大的肋骨碎片，这将在以后加以考虑。
• 
  
  Prim的算法（已修改） ：此Prim的算法创建了一个最小的生成树，对其进行了修改，以使边缘的所有权重均相同。 但是，它以这样一种方式实现，即着眼于单元而不是边缘。 内存量与迷宫的大小成正比。 在创建过程中，每个单元格可以具有以下三种类型之一：（1）“内部”：该单元格是迷宫的一部分并已在其中切出；（2）“边界”：该单元格不是迷宫的一部分且尚未在其中被切出，但位于在已经“内部”的单元格旁边；以及（3）“外部”：该单元格还不是迷宫的一部分，并且它的任何邻居都不是“内部”单元格。 我们从选择一个单元格开始，使其成为“内部”，然后将其所有邻居的类型设置为“边界”。 我们随机选择“边界”单元，并从相邻的“内部”单元之一中切入一个通道。 我们将“边界”单元的状态更改为“内部”，并将其所有邻居的类型从“外部”更改为“边界”。 当不再有“边界”单元时（即，没有“外部”单元，这意味着每个人都变成了“内部”），迷宫便完成了。 该算法创建的迷宫具有非常低的屈服指数，具有许多短死锁和相当简单的解决方案。 产生的迷宫与简化的Prim方法的结果非常相似，只是有一点点差异：只有在随机选择边界单元的情况下，生成树中的空隙才会被填充，而通过一个导致它的边界单元填充此单元的可能性是三倍。 另外，该算法非常快，比简化的Prim算法要快，因为它不需要编译和处理边列表。
• 
  
  Aldous-Broder算法：该算法有趣的是它是同质的，也就是说，它以相同的概率创建了给定大小的所有可能的迷宫。 另外，它不需要额外的内存或堆栈。 我们选择一个点并随机移动到相邻单元格。 如果我们进入未切割的单元格，则将前一个单元格中的通道剪切掉。 我们继续移动到相邻的单元，直到我们切开所有单元的通道。 该算法创建的迷宫式流速低，仅略高于Kraskal算法。 （这意味着对于给定的交易所，低收益率的迷宫比高收益率的迷宫要多，因为具有平均概率的迷宫同样也很低。）此算法的坏处在于它非常慢，因为它不对后者进行智能搜索单元，即实际上并不能保证完成。 但是，由于其简单性，它可​​以快速通过许多单元，因此它的完成速度比您想象的要快。 平均而言，完成所需的时间是标准算法的七倍，尽管在坏情况下，如果随机数生成器不断避开最后几个像元，则需要更长的时间。 如果边界墙被视为单个顶点，则可以将其实现为添加墙，即，例如，如果移动将我们移动到边界墙，则我们会沿边界传送到随机点，然后才继续移动。 在添加墙的情况下，它的工作速度几乎快一倍，因为沿边界墙的隐形传送可以更快地进入迷宫的远处。
• 
  
  威尔逊算法 ：这是Aldous-Broder算法的改进版本，它创建了具有完全相同纹理的迷宫（算法是同质的，即所有可能的迷宫都是以相等的概率生成的），但是威尔逊算法要快得多。 它需要占用多达迷宫大小的内存。 我们从随机选择的初始迷宫单元开始。 我们选择一个尚未属于迷宫的随机单元，并执行随机游走，直到找到已经属于迷宫的单元。 一旦迷路了迷宫的已创建部分，我们将返回到所选的随机像元，并通过将这些像元添加到迷宫中来切出整个路径。 更具体地说，当我们沿着路径返回时，我们在最后一次离开单元格时沿随机游走的方向切入每个单元格。 这样避免了沿返回路径出现回圈，从而使一个较长的通道与迷宫相连。 当所有细胞都附着到迷宫时，迷宫就完成了。 该算法具有与Aldous-Broder相同的速度问题，因为它可能花费大量时间来找到通往初始单元的第一条随机路径，但是在放置了几条路径后，迷宫的其余部分很快就被切掉了。 平均而言，它的运行速度是Aldous-Broder的五倍，而运行速度却比最佳算法慢了不到两倍。 值得考虑的是，在添加墙的情况下，它的工作速度是以前的两倍，因为整个边界墙最初都是迷宫的一部分，因此第一堵墙的连接要快得多。
• 
  
  查杀算法：此算法很方便，因为它不需要额外的内存或堆栈，因此由于不可能用尽内存，因此适合在较弱的计算机上创建巨大的迷宫或迷宫。 由于它没有需要经常遵循的规则，因此使用它修改和创建具有不同纹理的迷宫也是最容易的。 它几乎类似于递归回溯器，仅在当前位置附近没有创建任何像元。 我们进入“狩猎”模式并系统地扫描迷宫，直到在已剪切的单元格旁边找到一个未创建的单元格。 在这一阶段，我们再次开始在这个新位置进行切割。 当在“狩猎”模式下扫描所有细胞时，迷宫完成。 该算法倾向于创建高流速的迷宫，但不如递归backtracker高。 您可以强制它以较低的流速生成迷宫，更经常地进入“狩猎”模式。 由于花费了寻找最后一个细胞的时间，它的运行速度较慢，但​​并不比Kraskal算法慢很多。 如果您偶尔随机传送以避免递归回溯器固有的问题，则可以根据添加墙的原理来实现。
• 
  
  增长算法
  树（生长树算法） ：这是一种通用算法，可以创建具有不同纹理的迷宫。 所需的内存可以达到迷宫的大小。 每次剪切一个单元格时，我们都将其添加到列表中。 从列表中选择一个单元格，然后剪切到旁边未创建的单元格的段落。 如果当前单元格附近没有未创建的单元格，请从列表中删除当前单元格。 当列表中没有其他内容时，迷宫完成。 关于算法的有趣之处在于，根据您从列表中选择单元格的方式，可以创建许多不同的纹理。 例如，如果您始终选择最后添加的单元格，则此算法将变为递归回溯器。 如果始终随机选择单元格，则其行为与Prim算法相似，但不相同。 如果您始终选择添加到列表中最旧的单元格，那么我们将创建具有最低可能产量指数甚至比Prim算法更低的产量的迷宫。 如果通常选择最后一个单元格，但偶尔选择一个随机单元格，则迷宫将具有较高的流速，但解决方案又短又直接。 如果随机选择最近的一个单元，则迷宫的流速会很低，但解决方案会很长且曲折。
• 
  
  生长森林算法 ：这是一种更为通用的算法，结合了基于树和集合的类型。 它是树增长算法的扩展，该算法本质上包括同时扩展的多个实例。 我们首先将所有单元格随机分类为“新”列表； 此外，就像在Kruskal算法开始时一样，每个单元格都有自己的集合。 首先，通过将一个或多个单元格从“新”列表移到“活动”列表中来选择一个或多个单元格。 从“活动”列表中选择一个单元格，然后从“新”列表中剪切到下一个未创建的单元格的通道，将一个新单元格添加到“活动”列表中，并合并两个单元格的集合。 如果尝试切入迷宫的现有部分，则在单元格位于不同集合中并合并单元格时启用它，就像在Kraskal算法中所做的那样。 如果当前单元格附近没有“新”单元格，则将当前单元格移到“完成”的列表中。 当“活动”列表变为空时，迷宫完成。 最后，与Kruskal算法一样，我们合并所有剩余的集合。 您可以定期地通过将一个或多个单元格从“新”列表移动到“活动”列表来创建新树，就像开始时所做的那样。 通过控制原始树的数量和新创建的树的份额，您可以生成许多独特的纹理，并结合了树木生长算法已经灵活的参数。
• 
  
  埃勒算法 ：这是一种特殊的算法，因为它不仅比其他任何人都快，而且没有明显的偏差或缺点。 另外，创建内存时，可以最有效地使用内存。 它甚至不需要整个迷宫都在内存中，而是使用与行大小成比例的体积。 它会逐行创建一个迷宫，在字符串生成完成之后，算法不再将其考虑在内。 行中的每个单元格都包含在一个集合中； 如果两个单元格之间沿着已创建的迷宫路径，则它们属于同一组。 此信息使您可以在当前行中剪切段落，而无需创建循环或孤立的区域。 实际上，它与Kraskal算法非常相似，只是在这里一次形成一行，而Kraskal则在整个迷宫中浏览。 创建行包括两部分：随机连接该行中的相邻单元格，即 我们切出水平通道，然后将当前和下一行（即 切掉垂直通道。 在剪切水平通道时，我们不连接已经在同一集合中的单元格（因为否则将创建循环），并且在剪切垂直通道时，如果单元格具有单位大小，则必须连接一个单元格（因为如果保留它，它将创建一个隔离的区域）。 剪切水平通道时，如果它们位于同一组中，则我们将它们连接起来（因为它们之间现在有一条路径）；当剪切垂直通道时，如果它们不与该单元格连接，则将它们放在单独的一组中（因为现在它与迷宫的其余部分分开了） ） 创建始于以下事实：在连接第一行中的单元之前，每个单元都有其自己的集合。 在最后一行中连接单元后，创建完成。 有一个特殊的完成规则：到完成时，每个像元应位于同一集合中，以避免出现孤立区域。 （最后一行是通过组合尚不在同一集合中的每对相邻单元格来创建的。）最好使用循环的双向链接单元列表（可以是将单元格绑定到同一集合两侧的单元格对的数组）来实现该集合。在恒定时间内执行一组中相邻小区的插入，删除和验证。 该算法的问题是在迷宫的不同边缘处理中的不平衡。 为了避免纹理上出现污渍，您需要以正确的比例连接和跳过连接单元。
• 
  
  递归划分：此算法与递归回溯有点类似，因为它们都使用堆栈，但它不适用于过道，但适用于墙。 我们首先创建一个随机的水平或垂直墙，该墙与随机行或列中的可访问区域相交，并沿其随机放置空白区域。 然后，我们递归地对分隔墙生成的两个子区域重复此过程。 为了获得最佳结果，您需要根据区域的比例在水平或垂直选择中添加偏差，例如，宽度为高度的两倍的区域应更频繁地用垂直墙分开。 这是最快的算法，没有方向偏差，而且通常甚至可以与基于二叉树的迷宫竞争，因为它可以同时创建多个单元格，尽管它的明显缺点是长壁与迷宫内部相交。 该算法是一种嵌入式的分形迷宫，但是与其在每个单元格内部不断创建具有相同大小迷宫的固定大小的迷宫，不如将一个给定区域随机分为一个随机大小的迷宫：1x2或2x1。 递归除法不能用于切出通道，因为这会导致创建一个明显的解决方案，该解决方案要么沿外边缘延伸，要么直接与内部相交。
• 
  
  基于二叉树的迷宫 ：实际上，它们是最简单，最快的算法，但是创建的迷宫的纹理具有很高的偏差。 对于每个单元格，我们向上或向左切一个通道，但切勿双向切入。 在增加了壁的版本中，为向下或向右但不沿两个方向的每个顶点添加了壁段。 每个单元格都独立于所有其他单元格，因为在创建它时我们不需要检查其他一些单元格的状态。 因此，这是用于生成没有内存的迷宫的真实算法，不受创建迷宫大小的限制。 实际上，如果我们将左上角视为根，则这是一个二叉树，并且每个节点或单元都有一个唯一的父节点，该父节点是其上方或左侧的一个单元。 基于二叉树的迷宫与标准理想迷宫不同，因为它们中不能存在超过一半的细胞类型。 例如，它们之间永远不会有交叉路口，并且所有死胡同都有通道向上或向左引导，而永远不会向下或向右引导。 迷宫通常具有从左上角到右下角的对角线通道，并且从右下角到左上角的移动要容易得多。 您始终可以向上或向左移动，但不能同时在两个方向上移动，因此您始终可以确定性地沿对角线向上和向左移动，而不会遇到障碍。 您将有机会选择通过向下和向右移动而陷入死胡同。 , , , .
• 
  
  Sidewinder: , . : , , . , , , , , . , ( , ). , sidewinder . , sidewinder . , sidewinder , , . sidewinder , « ». , sidewinder — , , , , . sidewinder , , , .

演算法	死角百分比	型式	优先权	没有偏见？	同质的？	记忆	时间	％溶液
单路线	0	树	墙壁	是的	从不	N ^ 2	379	100.0
递归回溯	10	树	人行道	是的	从不	N ^ 2	27	19.0
猎杀	11（21）	树	人行道	是的	从不	0	100（143）	9.5（3.9）
递归除法	23	树	墙壁	是的	从不	N *	10	7.2
二叉树	25	许多	两者都	没有啦	从不	0 *	10	2.0
响尾蛇	27	许多	两者都	没有啦	从不	0 *	12	2.6
埃勒算法	28	许多	两者都	没有啦	没有啦	N *	20	4.2（3.2）
威尔逊算法	29日	树	两者都	是的	是的	N ^ 2	48（25）	4.5
Aldous-Broder算法	29日	树	两者都	是的	是的	0	279（208）	4.5
克拉斯卡尔算法	30	许多	两者都	是的	没有啦	N ^ 2	33	4.1
Prima算法（true）	30	树	两者都	是的	没有啦	N ^ 2	160	4.1
Prima算法（简体）	32	树	两者都	是的	没有啦	N ^ 2	59	2.3
Prima算法（已修改）	36（31）	树	两者都	是的	没有啦	N ^ 2	30	2.3
树木生长	49（39）	树	两者都	是的	没有啦	N ^ 2	48	11.0
森林生长	49（39）	两者都	两者都	是的	没有啦	N ^ 2	76	11.0

下表概述了用于创建上述理想迷宫的算法的特征。为了进行比较，添加了单路迷宫算法（理论上，单路迷宫是理想的）。列说明：

• : , , , 2D-. . , , , . 10% ( ) 49% ( ). Recursive Backtracker 1%. 66%: .
• : : , , . , , , , . , , .
• : , . . , , . Recursive Backtracker , , , . , , . , Hunt and Kill , , .
• : , . , . Sidewinder , . , . Hunt and Kill , , , .
• : . «» , . «» , , . «» , , . , .
• : , . , , (N), (N^2). , ( ). , , . Sidewinder , . , .
• : , , , . , ( 10), . 100x100 Daedalus. , , , .
• : , , . , 100x100 . . «» . , . , . , , , .

解决迷宫的方法有很多，每种都有自己的特点。以下是特定算法的列表：

• 
  
  沿着墙壁（墙追随者） ： . («»), . ( ). , ( ) . , . , , . , , , . 3D- , 3D- 2D-, .. , -, -, .
• 
  
  : , «» , . 2D- , , .. . , , . . , , . , , . , , . , , — -1, — 1. , , .. 360 , «». , «», , , , , . , , . , — , .
• 
  
  : (Chain algorithm) , ( ) . , , . , . , , . , . ( ) , . . , , . «» , . , , , . , . , .
• 
  
  Recursive backtracker: , . , . : ( ), «», , , «», , . , , «»; «» . (backtracking) , , . , . , , .
• 
  
  (Trémaux's algorithm): . recursive backtracker : , . , . , , . , , , . ( , .) , (.. ), , , , (.. , ). , , , , , . , . , , .
• 
  
  (Dead end filler) : . , . , , . , . , , . , , .
• 
  
  Cul-de-sac filler : , , . dead end filler, , . ( — , , ) , . dead end filler. , , , , . , , , dead end filler.
• 
  
  Blind alley filler : , , . , . — , , . , , cul-de-sac filler, . . , , , , . , , , ( ). , , . , cul-de-sac filler - , collision solver , - .
• 
  
  Blind alley sealer : blind alley filler , , . . . , , blind alley filler, . . , , , , . , , . , . , , . , , .
• 
  
  (Shortest path finder): , , . , , . collision solver, , , «» , ( ), «» , , . «», , . , - , . , , , A* , .
• 
  
  (Shortest paths finder) : , . , , , , , , , - , . , , , «» , , , . , , , , . , .
• Collision solver: "amoeba" solver. . , . «» , ( ). « » ( ), , . «», , , , . ( , «», . , , , .) , shortest paths finder, ( ) ( ).
• Random mouse: , , .. , . 180 , . , , . , , .

		?		?	?	?	?
Random Mouse	1个	没有啦		/	没有啦	是的	没有啦
Wall Follower	1个	没有啦		/	是的	是的	是的
	1个	没有啦		/	是的	是的	是的
	1个	是的	+	没有啦	是的	没有啦	是的
递归回溯	1个	是的	你是	没有啦	是的	没有啦	是的
Tremo算法	1个	是的	你是	内部/上方	没有啦	没有啦	是的
死角填充	全部+	没有啦	迷宫	结束	没有啦	是的	是的
死囊填充物	全部+	没有啦	迷宫	结束	没有啦	是的	是的
盲巷封闭机	全部+	是的	迷宫	没有啦	没有啦	没有啦	是的
盲巷填充物	全部	是的	迷宫	结束	没有啦	是的	没有啦
碰撞求解器	最短	是的	你+	没有啦	没有啦	没有啦	是的
搜索最短路径	最短	是的	你+	没有啦	是的	没有啦	是的
搜索最短路径	最短1	是的	你+	没有啦	是的	没有啦	是的

下表简要列出了上述迷宫求解算法的特征。 根据这些标准，可以对解决迷宫的算法进行分类和评估。 列说明：

• 解决方案：描述由算法找到的解决方案和算法的动作（如果有的话）。 该算法可以选择一种解决方案，也可以保留几种解决方案。 另外，解决方案可以是任何路径或最短路径。 死角填充物和死胡同填充物（以及处理不可达区域时的盲巷封闭器）会留下所有解决方案，但是，它们也可能留下不在任何解决方案路径中的通道，因此我将其标记为“全部+ ”。
• 保修：是否保证算法能找到至少一个解决方案？ 对于随机鼠标，指示“否”，因为不能保证其完成；对于墙壁追随者和学院的算法，指示“否”，因为如果目标在岛内，他们将无法找到解决方案。 死角填充物和死角填充物表示为“死角”，因为在柳条迷宫中它们可能找不到解决方案。
• 优先级：解决迷宫的算法有两种：将“ you”（位于迷宫中）优先或将迷宫优先。 如果给予您优先权，则我们有一个点（表中标有“ You”）或许多点（“ You +”），算法会尝试从迷宫的起点到终点绘制它们。 如果优先考虑迷宫，那么我们将迷宫作为一个整体进行检查，并丢弃无用的段落。
• 对人可用：人可以在真正的迷宫中还是从上方查看地图时使用算法求解迷宫。 可以将优先于“您”的某些算法实现为迷宫内部（或上方）的人，而将优先于迷宫的某些算法可以实施为人，但仅在迷宫之上。 其他算法过于复杂，只有在计算机中才能可靠实现。
• 独立通过：算法可以在任何地方执行。 一些算法要求迷宫具有明显的段落，或者用图形术语来说，各个顶点之间的边缘清晰，或者在计算机上实现时一个像素中的段落。 墙跟随者，承诺算法和电路算法仅在您的一侧需要墙。 递归回溯器和最短路径查找器通过开放空间路由它们。
• 不需要内存：您是否需要额外的内存或堆栈来实现算法。 有效的算法仅需要迷宫本身的位图，并且在解决迷宫的过程中不需要向迷宫添加标记。
• 快速：决策过程是否快速。 最有效的算法足以查看迷宫的每个单元一次，或者它们可以完全跳过部分迷宫。 运行时间应与迷宫的大小成正比，即O（n ^ 2），其中n是沿一侧的单元数。 随机鼠标的速度很慢，因为不能保证其完成效果，而盲巷填充物可能会解决每个叉子的迷宫。

迷宫的其他操作

除了创建和解决迷宫以外，您还可以对它们执行其他操作：

• 
  
  填充：这是一个“快速而又肮脏的”功能，但是仍然有用，可以通过一次调用Fill或FloodFill图形库过程来实现。 我们在开始时执行段落的FloodFill，如果未淹没结尾，则迷宫没有解决方案。 在迷宫中，其入口和出口在边缘，我们执行一堵墙的FloodFill，其余边缘标记解决方案。 在开始和结束都在内部的迷宫中，我们执行边界墙的FloodFill，如果未移除出口墙，则无法通过沿墙壁跟踪来解决此迷宫。 创建迷宫和其他功能的许多方法在某些位置使用迷宫的“填充”。
• 
  
  隔离去除剂：改变迷宫，使其不具有迷宫其余部分无法通行的部分。 通过移除将这些部分与迷宫的其余部分相连的壁来进行。 我们从迷宫的副本开始，然后在开头附近填充段落。 我们扫描迷宫（最好以随机顺序，但要访问所有可能的细胞）以检查是否存在与填充细胞相邻的未填充细胞。 我们在原始迷宫的这一点上删除墙段，在新的位置填充迷宫，然后重复直到所有部分都填满。 此功能用于创建编织和图案迷宫。
• 
  
  去除环路：更改迷宫，使其中没有环路和墙壁未连接任何东西，并且迷宫的每个部分都只能以一种方式从任何点到达。 此功能的实现几乎类似于隔离区域的移除，只是我们将墙壁视为通道，反之亦然。 我们从迷宫的副本开始，然后填充外墙。 我们扫描迷宫（最好以随机顺序，但要访问所有可能的墙顶），以检查迷宫旁边是否存在未填充的墙壁。 此时，添加一个将墙的两个部分连接到原始迷宫的墙段，在这个新点填充迷宫，然后重复进行直到所有部分都装满为止。 此功能用于创建模板迷宫，并可用于将柳条迷宫转换为理想的迷宫，但仍然与原始迷宫相似。
• 
  
  搜索瓶颈 ：搜索迷宫中所有解决方案通过的通道或相交点的迷宫。 为此，请使用左手方法沿墙开始跟踪以获得左解，并使用右手方法沿墙开始跟踪以获得右解。 这两种解决方案很常见的地方就是瓶颈。 但是，此技术仅适用于迷宫，可以通过沿墙跟随成功解决。 在其他迷宫中，要查找瓶颈，您需要找到任何解决方案，并运行盲巷封闭器（如果迷宫将迷宫中的入口或出口视为大死角，这会使迷宫无法解决）。 穿过封闭通道的溶液路径部分是瓶颈。

算法实现

• Daedalus ：上述所有用于创建和解决迷宫的算法均在Daedalus中实现，Daedalus是免费的，可下载Windows程序。 与Daedalus一起完成的还有完整的源代码。