程序员的语言学（这不是错字）

写数学比写物理学要难（因此很有趣）。 但是，我希望您至少阅读疯狂的C程序的示例。


怪物可以从完全无害的事物中生长出来。 以子串游戏为例。 我们写一个字母a和b的字符串，并选择字符1到字符2的子字符串，从2到4，从3到6，从n到2n，直到主字符串的长度足够。 我们的任务是确保在这些子字符串中，较短的不再出现。 我什至写了一个SQL解析器：

declare @s varchar(max) = 'abbbaaaaaaab' declare @n int=1 declare @sub table (n int, sub varchar(max)) while @n*2<=len(@s) begin insert into @sub select @n,substring(@s,@n,@n+1) set @n=@n+1 end select *,(select max(sub) from @sub I where In>On and charindex(O.sub,I.sub)>0) as FoundMatch from @sub O order by 1 

这是示例输出：



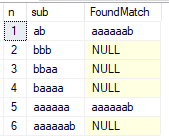
如您所见，子字符串1和5没有通过测试。 我们可以删除最后一个字符，得到的11个字符的字符串'abbbaaaaaaaa'将通过测试。 事实证明，这是满足此条件的两个字符的字母表中最长的字符串。

对于一个字符的字母，最大字符串长度为3，然后纯粹出于技术原因。 事实证明，对于任何数量的字母来说，最大长度是有限的。 因此，我们有：

$$

$$f（1）= 3$$

$$

$$f（2）= 11$$

$$

$$f（3）= ???$$

测试您的直觉，以三个字母组成的字符串可以多长时间。 100？ 1000？ 实际上，它远远超过Googol，而且远远超过GoogolPlekh。

$$

$$f（3）> 2 \ uparrow ^ {7198} 158836$$

而且我必须花时间证明射手的实力。

箭头（过度操作）

我们使用乘法以免编写许多加法运算：

$$

$$2 * 5 = 2 + 2 + 2 + 2 + 2$$

我们使用幂运算以免编写许多乘法：

$$

$$2 ^ 3 = 2 * 2 * 2$$

将加法视为级别0的运算，将乘法视为1，将幂运算作为2，我们可以引入运算符“箭头”，例如，

$$

$$3 \ uparrow 3 = 3 ^ {（3 ^ 3）} = 3 ^ {27} = 7'625'597'484'987$$

请注意，括号在这里已经很重要。 下一级是两个箭头操作：

$$

$$3 \ uparrow \ uparrow 3 = 3 \ uparrow（3 \ uparrow 3）= 3 \ uparrow 7625597484987 = 3 ^ {3 ^ {... ^ 3}}$$

最后一个三元组金字塔的高度为70亿，这个数字已经远远超过googol和googolpleks。 我们将这个巨大的数字表示为Darkness （在古老的俄语中是这样的数字），并尝试采取进一步的措施：

$$

$$3 \ uparrow ^ 3 3 = 3 \ uparrow \ uparrow \ uparrow 3 = 3 \ uparrow \ uparrow（3 \ uparrow \ uparrow 3）= 3 \ uparrow \ uparrow {黑暗} = 3 \ uparrow 3 \ uparrow 3 ... \ Uparrow 3$$

（很多次）...甚至已经可以想象到这个数字有多大。 请注意，当有很多箭头时，我们在顶部写一个中继器。 这样你就可以了解

$$

$$f（3）> 2 \ uparrow ^ {7198} 158836$$

还有更多

可以这么说，使用箭头仅创建大数字中的最小数字。 通过与快速增长的功能进行比较，可以在一定规模上衡量功能的增长率。 此层次结构中的第一个功能对应于加法，第二个功能对应于乘法，第三个功能对应于箭头，第n个至n-2个箭头（大约，不完全是）。 但是你可以定义

$$

$$f_w（n）= f_n（n）$$

对于n = 3的这种函数可以与一个箭头相提并论，对于n = 4的具有两个箭头，并且随着参数n的增长，它在任何静态数目的箭头上都超过了函数的增长。

您可以走得更远： $$$f_w，f_ {w + 1}，f_ {w + n}，f_ {w2}，f_ {w ^ 2}，f_ {w ^ w}，f_ {w ^ {w ^ {w}}}，f_ \ epsilon$ 这些功能按序号索引，或者在俄罗斯文学中按序号索引。 带有初始序数结构的图片在本文之前，但是它们延伸得更远，而且开始更远

一点神秘主义

欧米茄无尽的金字塔赋予序数 $$$\ epsilon_0$ 。 阅读有关此序号度量其增长的函数的信息。 事实证明，一个函数增长如此之快，以至于形式上的算术原理上根本无法证明该函数已定义！

当然，您知道戈德尔定理，其中有无法证明的陈述。 但是，通常，这种说法的唯一例子就是哥德尔的结构本身（“我无法证明”）。 古德斯坦定理就是这种陈述的一个很好的例子。

而且，事实证明，普通话以某种方式衡量理论的力量 。 形式算术的“强度”是 $$$\ epsilon_0$ ， 简化的Kripke-Plateka集理论具有Feferman-Schutte序数等的优势。

锡-数学止血带-C语言竞赛

举行了比赛以产生大量比赛。 不，对Turing机器进行编程仍然太残酷，因此C被用于sizeof（int）= infinity的某些抽象无限机器。 您还可以使用malloc（），并且像堆栈一样，内存量是无限的。 仅限制程序长度-程序必须容纳512个字节（不包括空格），但是允许使用预处理程序（#define）。

结果发布在数学网站上 。 同时检查一个真正的数学家的网站设计。 结果在这里 。 这是程序的文本，它排在第二位，给出了

$$

$$f_ {w ^ w}（10 ^ {500}）$$

 typedef int J; JP(J x,J y) { return x+y ? x%2 + y%2*2 + P(x/2,y/2)*4 : 0 ;} JH(J z) { return z ? z%2 + 2*H(z/4) : 0 ;} JI(J f,J e,J r){ return f ? P(P(f,e),r) : r ;} JM(J x,J e) { return x ? I(x%2, M(e,0), M(x/2, e+1)) : 0 ;} JD(J,J); JE(J f,J e,J r,J b) { return e ? E(1, D(e,b), I(b-1, D(e,b), I(f-1,e,r)), b) : I(f-1,e,r) ; } JD(J x,J b) { return x ? E( H(H(x)), H(H(x)/2), H(x/2), b) : 0 ;} JF(J x,J b) { return x ? F(D(x,b+1),b+1) : b ;} JG(J x) { return F(M(x,9), 9) ;} J f(J n,J x) { return n ? f(n-1, G(x ? f(n,x-1) : n)) : G(x) ;} J g(J x) { return f(x,x) ;} J h(J n,J x) { return n ? h(n-1, g(x ? h(n,x-1) : n)) : g(x) ;} J main(void) { return h(g(9),9) ;} 

优胜者的计划文本较长，我只想显示它的开始位置：

 #define R { return #define PP ( #define LL ( #define TS (v, y, c, #define C ), #define X x) #define F );} 

但是，即使是比赛的组织者，也很难评估结果的数量（写得非常大 ）

繁忙的海狸

好吧，足以应付小数目，让我们做大数目。 想象一下，已经组织了一场普遍竞赛来编写一个程序以产生最大数量的竞赛。 由于程序数不超过512个字符，因此，总会有绝对的赢家。 让我们将其指定为BB（512） -busy beaver function 。

显然，BB（1024）>> BB（512）。 但是BB功能增长有多快？ 事实证明，它的增长速度超过了我们所遇到的一切。 BB函数本身在算法上无法解决；无法在计算机上计算。 但是随着有效程序长度的增加，我们可以实现越来越多的新想法。 因此，BB的增长速度快于任何算法可确定的功能。

大脚

好吧，足以应付小数目，让我们做大数目。 啊，我已经说过了吗？ 运行BB（BB（n））会很酷。 但是，由于BB无法计算，因此存在技术难题（这种功能在具有Oracle的Turing机器中是可计算的-不要将oracle与Oracle DBMS混淆）。

但是，您可以更轻松地执行此操作，而不是使用程序 ，而是考虑使用长度为n的量词的公式 。 量词公式与某物是否可计算无关紧要。 因此，您至少可以采用BB（1,000,000,000）函数，并将其应用于您自己的BB（BB（BB（1,000,000）））次。 这只是首先想到的。

最多可以由n个字符的公式表示的最大数字由FOOT（n）表示。

$$

$$大脚=脚^ {10}（10 ^ {100}）$$

聚苯乙烯

对于下一篇文章，我想了解重点关注的内容，请参加调查