
实验数据直方图有什么问题
任何工业企业产品质量管理的基础都是实验数据的收集和后续处理。
实验结果的初始处理包括比较有关数据分布规律的假设,该假设以最小的误差描述了所观察样品的随机变量。
为此,以直方图的形式显示样本,包括
以长度间隔构造的列
。
确定测量结果的分布形状还需要解决许多问题,这些问题的求解效率因不同的分布而异(例如,使用最小二乘法或计算熵估计值)。
此外,还必须确定分布,因为所有估计值(标准差,超额,峰度等)的散布也取决于分布定律的形式。
识别实验数据分布形式的成功取决于样本量,如果样本量很小,分布特征将被样本本身的随机性所掩盖。 实际上,由于各种原因,不可能提供大的样本大小,例如,大于1000。
在这种情况下,当间隔序列需要进一步分析和计算时,以最佳方式在间隔中分配样本数据非常重要。
因此,为了成功识别,有必要解决分配间隔数k的问题。
A. Hald在书[1]中广泛地认为,当在这些间隔上构建的直方图的逐步包络最接近总体总体的平滑分布曲线时,存在最佳的分组间隔数。
接近最佳值的实际迹象之一是直方图中的下降消失,然后认为最大k接近最佳值,此时直方图仍保持平滑特征。
显然,直方图的类型取决于属于随机变量的间隔的构造,但是,即使在均匀划分的情况下,对于这种构造的令人满意的方法仍然不可用。
可以认为是正确的分区导致了这样一个事实,即假设的连续分布密度(直方图)的分段常数函数引起的近似误差将最小。
困难是由于估计密度未知这一事实引起的;因此,间隔的数量强烈影响最终样本的频率分布形式。
对于固定的样本长度,分配间隔的扩大不仅会导致进入它们的经验概率的细化,而且还会导致不可避免的信息丢失(从一般意义上和在概率密度分布曲线的意义上来说),因此,如果进一步进行不合理的扩大,则所研究的分布会过于平滑。
一旦出现,在直方图下对范围进行最佳划分的任务就不会从专家的视野中消失,并且直到对解决方案的唯一确定的观点出现之前,该任务将仍然有意义。
选择用于评估实验数据直方图质量的标准
众所周知,皮尔逊准则要求将样本划分为多个区间-在这些区间中,将评估采用的模型与比较样本之间的差异。
其中:
-实验频率
;
-同一列中的频率值; m个直方图列。
但是,在通常用于构造直方图的恒定长度间隔的情况下,此标准的应用效率低下。 因此,在关于Pearson准则有效性的工作中,根据公认的模型,考虑的间隔不是等长,而是等概率。
然而,在这种情况下,相等长度的间隔数和相等概率的间隔数相差数倍(除了等概率分布外),这使人们怀疑[2]中得到的结果的可靠性。
作为近似标准,建议使用熵系数,其计算如下[3]:
其中:
-第i个间隔中的观察次数
使用熵系数和numpy.histogram模块评估实验数据直方图质量的算法
使用该模块的语法如下[4]:
numpy.histogram(a,箱= m,范围=无,范数=无,权重=无,密度=无)
我们将考虑在numpy.histogram模块中实现的用于找到直方图分裂间隔的最佳数量
m的方法:
•
'auto' -
'sturges'和
'fd'的最大等级,提供良好的性能;
•
'fd'(Freedman Diaconis Estimator) -一种可靠的(抗排放)评估器,考虑了数据的可变性和大小;
•
“ doane” -变形估计的改进版本,可更准确地处理具有非正态分布的数据集;
•
“斯科特”是一个不太可靠的评估者,它考虑了数据的可变性和大小;
•
“石头” -评估者基于对误差平方的估计值的交叉检查,可以认为是斯科特规则的概括;
•
“大米” -评估师不考虑可变性,而只考虑数据的大小,常常高估了所需间隔的数量;
•
“ sturges” -方法(默认情况下),仅考虑数据大小,仅对高斯数据最佳,而低估了大的非高斯数据集的间隔数;
•
“ sqrt”是Excel和其他程序使用的数据大小的平方根估计量,可快速轻松地计算间隔数。
为了开始描述算法,我们改用numpy.histogram()模块来计算熵系数和熵误差:
from numpy import* def diagram(a,m,n): z=histogram(a, bins=m) if type(m) is str:
现在考虑算法的主要阶段:
1)我们形成一个对照样品(以下称为“大样品”),
该样品
满足处理实验数据中的误差要求 。 从一个大样本中,通过删除所有奇数个成员,我们形成一个较小的样本(以下称为“小样本”);
2)对于所有评估者'auto','fd','doane','scott','stone','rice','sturges','sqrt',我们从一个大样本中计算出熵系数ke1和误差h1以及熵系数ke2小样本的误差h2以及差的绝对值-abs(ke1-ke2);
3)将评估器的数值控制在至少四个间隔的水平上,我们选择提供绝对差最小值abs(ke1-ke2)的评估器。
4)对于选择评估者的最终决定,我们在一个直方图上建立了大样本和小样本的分布,评估者提供了最小abs值(ke1-ke2),第二个评估者提供了最大abs值(ke1-ke2)。 在第二个直方图中,较小样本中出现了其他跳跃,这确认了第一个评估器的正确选择。
考虑从出版物[2]的数据样本中提出的算法的工作。 数据是通过从500个空白中随机选择80个空白并随后对其质量进行测量而获得的。 工件必须具有以下限制的质量:
公斤 我们使用以下清单确定最佳直方图参数:
上市 import matplotlib.pyplot as plt from numpy import* def diagram(a,m,n): z=histogram(a, bins=m) if type(m) is str:
我们得到:
样品的标准偏差(n = 80):0.24
样本的数学期望(n = 80):17.158
样品的标准偏差(n = 40):0.202
样本的数学期望(n = 40):17.138
ke1 = 1.95,h1 = 0.467,ke2 = 1.917,h2 = 0.387,dke = 0.033,m =自动
ke1 = 1.918,h1 = 0.46,ke2 = 1.91,h2 = 0.386,dke = 0.008,m = fd
ke1 = 1.831,h1 = 0.439,ke2 = 1.917,h2 = 0.387,dke = 0.086,m =杜安
ke1 = 1.918,h1 = 0.46,ke2 = 1.91,h2 = 0.386,dke = 0.008,m =斯科特
ke1 = 1.898,h1 = 0.455,ke2 = 1.934,h2 = 0.39,dke = 0.036,m =石头
ke1 = 1.831,h1 = 0.439,ke2 = 1.917,h2 = 0.387,dke = 0.086,m =水稻
ke1 = 1.95,h1 = 0.467,ke2 = 1.917,h2 = 0.387,dke = 0.033,m = urge
ke1 = 1.831,h1 = 0.439,ke2 = 1.917,h2 = 0.387,dke = 0.086,m =平方根
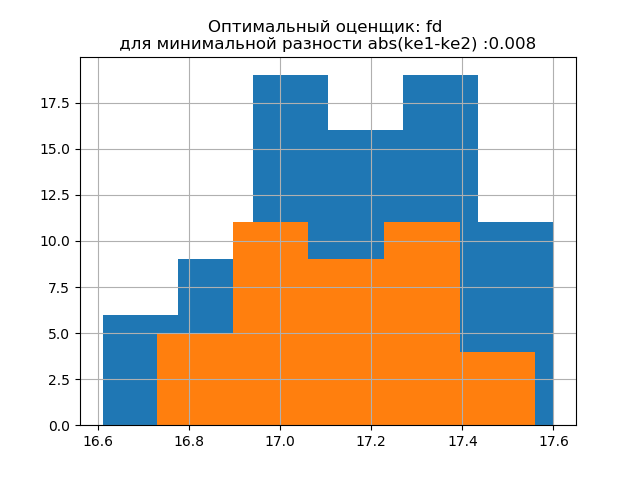
大样本的分布形式类似于小样本的分布形式。 从脚本中可以看出,
“ fd”是一个可靠的(抗排放)评估器,它考虑了数据的可变性和大小。
在这种情况下,小样本的熵误差甚至略有降低:h1 = 0.46,h2 = 0.386,而熵系数从k1 = 1.918到k2 = 1.91略有下降。
大样本和小样本的分布模式不同。 正如描述所暗示的那样,“ doane”是“ sturges”得分的改进版本,适用于具有非正态分布的数据集。 在这两个样本中,熵系数都接近于2,并且分布也接近于正态,与先前的样本相比,此直方图上的一个小样本中出现了额外的跳跃,另外表明了对评估器
“ fd”的正确选择。
我们使用以下关系式为参数
mu = 20,sigma = 0.5和size = 100生成两个新的正态分布样本:
a= list([round(random.normal(20,0.5),3) for x in arange(0,100,1)])
所开发的方法适用于使用以下程序获得的样本:
上市 import matplotlib.pyplot as plt from numpy import* def diagram(a,m,n): z=histogram(a, bins=m) if type(m) is str:
我们得到:
样品的标准偏差(n = 100):0.524
样本的数学期望(n = 100):19.992
样品的标准偏差(n = 50):0.462
样本的数学期望(n = 50):20.002
ke1 = 1.979,h1 = 1.037,ke2 = 2.004,h2 = 0.926,dke = 0.025,m =自动
ke1 = 1.979,h1 = 1.037,ke2 = 1.915,h2 = 0.885,dke = 0.064,m = fd
ke1 = 1.979,h1 = 1.037,ke2 = 1.804,h2 = 0.834,dke = 0.175,m = doane
ke1 = 1.943,h1 = 1.018,ke2 = 1.934,h2 = 0.894,dke = 0.009,m =斯科特
ke1 = 1.943,h1 = 1.018,ke2 = 1.804,h2 = 0.834,dke = 0.139,m =石头
ke1 = 1.946,h1 = 1.02,ke2 = 1.804,h2 = 0.834,dke = 0.142,m =水稻
ke1 = 1.979,h1 = 1.037,ke2 = 2.004,h2 = 0.926,dke = 0.025,m = urge
ke1 = 1.946,h1 = 1.02,ke2 = 1.804,h2 = 0.834,dke = 0.142,m = sqrt
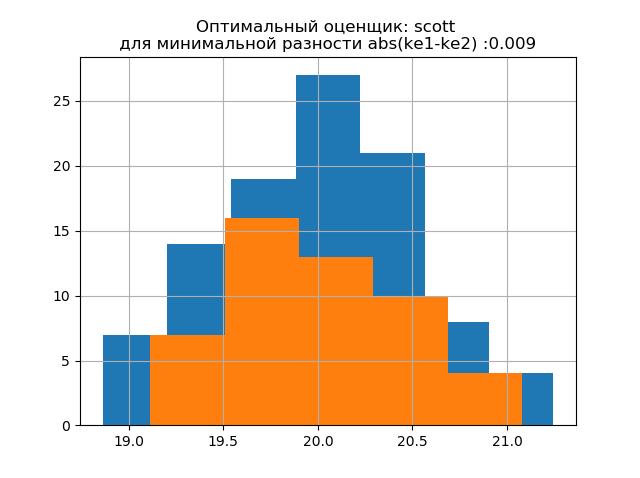
大样本的分布形式类似于小样本的分布形式。 从描述中可以看出,
“斯科特”是一种可靠性较低的评估器,它考虑了数据的可变性和大小。
在这种情况下,小样本的熵误差甚至会略有下降:h1 = 1.018和h2 = 0.894,而熵系数则从k1 = 1.943到k2 = 1.934略有下降。 。 应该注意的是,对于新样本,我们具有与上一个示例相同的更改参数的趋势。

大样本和小样本的分布模式不同。 从描述中可以
看出 ,
“ doane”是
“ sturges”估计值的改进版本,可以更准确地处理具有非正态分布的数据集。 在两个样本中,分布都是正态的。 与之前的直方图相比,此直方图上的小样本中出现了其他跳跃,这另外表明
“斯科特”评估器的正确选择。
使用抗锯齿进行直方图比较分析
平滑基于大样本和小样本的直方图,可以从保留较大样本中包含的信息的角度更准确地确定其身份。 将最后两个直方图想象成平滑函数:
上市 from numpy import* from scipy.interpolate import UnivariateSpline from matplotlib import pyplot as plt a =array([20.525, 20.923, 18.992, 20.784, 20.134, 19.547, 19.486, 19.346, 20.219, 20.55, 20.179,19.767, 19.846, 20.203, 19.744, 20.353, 19.948, 19.114, 19.046, 20.853, 19.344, 20.384, 19.945, 20.312, 19.162, 19.626, 18.995, 19.501, 20.276, 19.74, 18.862, 19.326, 20.889, 20.598, 19.974,20.158, 20.367, 19.649, 19.211, 19.911, 19.932, 20.14, 20.954, 19.673, 19.9, 20.206, 20.898, 20.239, 19.56,20.52, 19.317, 19.362, 20.629, 20.235, 20.272, 20.022, 20.473, 20.537, 19.743, 19.81, 20.159, 19.372, 19.998,19.607, 19.224, 19.508, 20.487, 20.147, 20.777, 20.263, 19.924, 20.049, 20.488, 19.731, 19.917, 19.343, 19.26,19.804, 20.192, 20.458, 20.133, 20.317, 20.105, 20.384, 21.245, 20.191, 19.607, 19.792, 20.009, 19.526, 20.37,19.742, 19.019, 19.651, 20.363, 21.08, 20.792, 19.946, 20.179, 19.8]) b=[a[i] for i in arange(0,len(a),1) if not i%2 == 0] plt.title(' \n abs(ke1-ke2)' ,size=12) z=histogram(a, bins="fd") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label=' n=100') z=histogram(b, bins="fd") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label=' n=50') plt.legend(loc='best') plt.grid() plt.show() plt.title(' \n abs(ke1-ke2)' ,size=12) z=histogram(a, bins="doane") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label=' n=100') z=histogram(b, bins="doane") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label=' n=50') plt.legend(loc='best') plt.grid() plt.show()
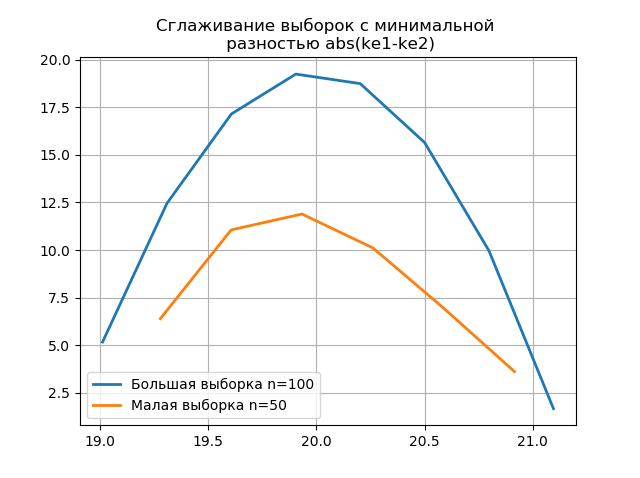
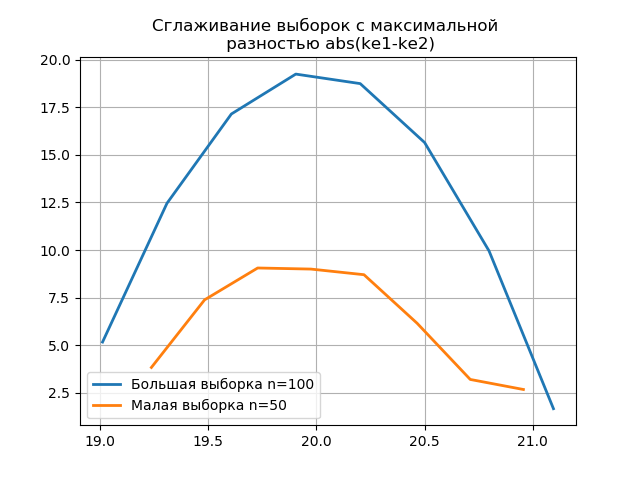
与先前的平滑直方图相比,在平滑直方图的图形上,小样本中出现了其他跳跃,这也进一步表明了对
斯科特评估器的正确选择。
结论
文章中提出的计算方法在生产中常见的小样本范围内证实了使用
熵系数作为维持样本信息含量同时减少样本量的准则的效率。 考虑使用具有内置评估程序的最新版本的numpy.histogram模块的技术-'auto','fd','doane','scott','stone','rice','sturges','sqrt',这些足以进行优化间隔估计的实验数据分析。
参考文献:
1.暂停A.数理统计与技术应用。 -莫斯科:出版社。 点燃。,1956
2. Kalmykov V.V.,Antonyuk F.I.,Zenkin N.V.
确定用于区间估计的实验数据分组类别的最佳数量//南西伯利亚科学公报。— 2014. —第3号。 56-58。
3. Novitsky P. V.误差的熵值的概念//测量技术— 1966年—第7号。 11-14。
4.numpy.histogram-NumPy v1.16手册