Geekly articles weekly

从程序员的角度来看Monad（以及一些类别理论）

引言


如何发现一个人了解什么是单子？ 他本人将在交流的前5分钟内告诉您有关此事，并且一定会尝试解释。 他还将撰写有关此文字的文章，并在可能的情况下将其发布在某处，以便其他所有人也了解什么是monad。


在函数式程序员中，特别是在Haskell上，单子函数已成为本地模因。 从特殊情况开始，并立即给出使用示例，他们经常被尝试解释。 因此，听众可能无法理解该概念的主要本质，而monads仍将保持黑魔法，或者仅仅是一种在纯功能语言中消除副作用的方法。


我将首先讨论类别理论的基本概念，然后从实践的角度出发，我们将对monad进行定义，并发现实际上，许多程序员在其表现形式之一中使用了这种强大的抽象。


我的演讲主要基于Bartosz Milewski的著作《程序员的分类论》，该书是一系列博客文章 ，以PDF格式提供 ，最近已发表在纸上。


这些示例在Haskell中提供，假定读者熟悉该语言的语法和基本概念。 在提到的书中，有一些使用C ++编写的示例，您可以比较代码的纯净度和可理解性。



分类目录


定义


类别本身是非常简单的结构。 类别是对象和对象之间的态素的集合。 形态可以看作是连接对象的单向箭头。 在一般情况下，对对象本身的本质一无所知。 范畴论不适用于对象，而是适用于态射，或更确切地说，适用于其构成 。


使用以下表示法：


  • Ob C - C类对象；
  • Hom C （A，B）-从A到B的态射;
  • g∘f是态射f和g的成分。

在定义类别时，态射还受到其他限制：


  1. 对于一对态f和g，如果f是从A到B的态（f∈Hom（A，B）），g是从B到C的态（g∈Hom（B，C）），则存在一个成分g∘ f是从A到C的态（g∘f∈Hom（A，C））。
  2. 对于每个对象，给出了一个同构态id A∈Hom（A，A）。

任何类别都必须满足两个重要的属性（类别理论的核心）：


  1. 组合物的缔合性：h∘（g∘f）=（h∘g）∘f;
  2. 具有等态同构的组合：如果f∈Hom（A，B），则f∘id A = id B∘f = f。

类别非常容易且自然地可视化为有向图。 原则上，如有必要，可以通过添加态素和相同态素的成分将任何有向图扩展到一个类别。



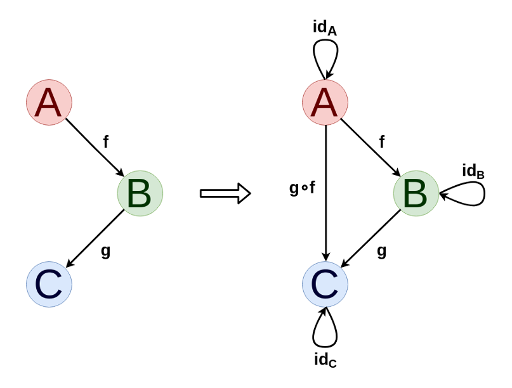
对于任何类别，您都可以定义一个对偶类别 （用C op表示），其中通过旋转原始类别的箭头获得同态，并且对象相同。这使我们能够制定对偶陈述和定理，当箭头倒置时，其对数不变。


对象和词素不一定形成集合（在经典意义上，从集合论出发），因此，在通常情况下，使用短语“对象类”。 仍然包含对象和态射类的类别的类别称为小类别 。 此外，我们将仅与他们合作。


类型和功能


, Haskell, — . , Int Bool — , Int -> Bool — .


id, :


id :: a -> a
id x = x

— , Haskell :


f :: a -> b
g :: b -> c
g . f :: a -> c
(g . f) x = g (f x)

, , — , Set. , — , : . bottom, _|_. , , , bottom. Haskell, , Hask. , Set. , , : HomC(A, B) ∈ C. , a -> b — Haskell.


.


Void, ( ). absurd, , , Void, :


absurd :: Void -> a

Unit, — , (). unit , :


unit :: a -> Unit
unit _ = ()

— Bool:


data Bool = True | False

, Void, Unit Bool.


Void , absurd, Bool, Unit. , Void, , .


Bool -> Unit , unit, . Unit -> Bool . (), True, False. , Unit Bool:


true, false :: a -> Bool
true _ = True
false _ = False

Bool Bool — , 4 ( n — 22n): id, true false, , not:


not :: Bool -> Bool
not True = False
not False = True

, :



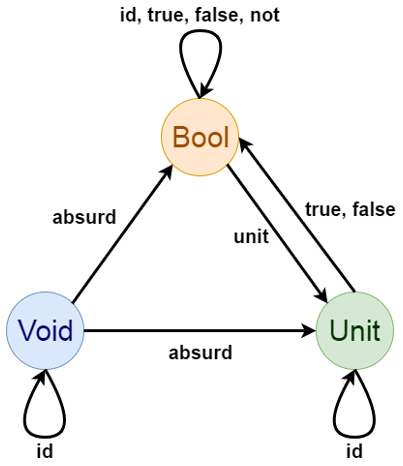
Haskell- .



— . , C D, F . -, C D. a — C, F a — D, . -, : f :: a -> b C F f :: F a -> F b D.



, " " :


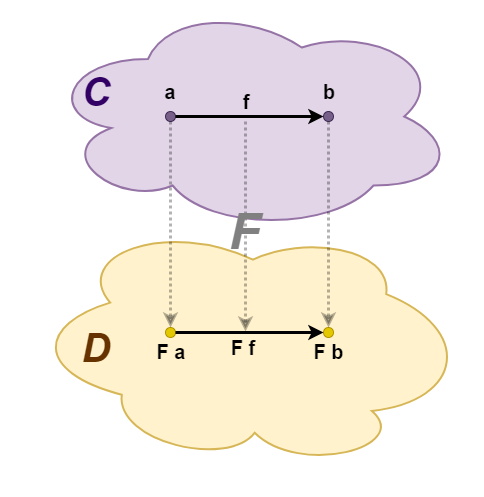
  1. h = g ∘ f, F h = F g ∘ F f.
  2. ida — a, F ida = idF a — F a.

, "" : , , . , , () . , .


. , F :: C -> D G :: D -> E G . F :: C -> E. , , , , . IdC, IdD IdE. , , .



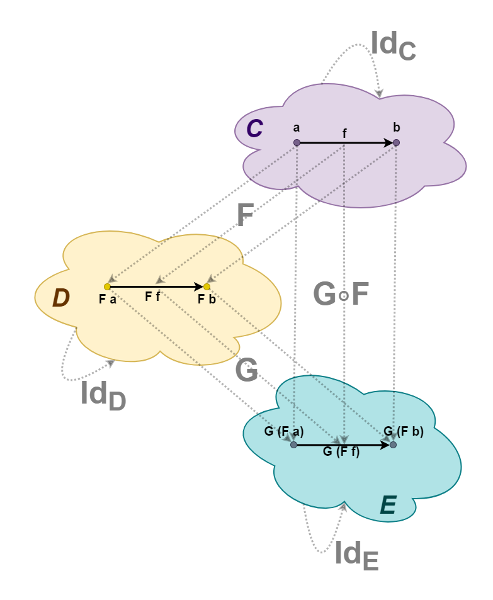
, , -, — (). , Cat ( ).


Haskell . , , - , .


Maybe , a Maybe a ( Maybe !):


data Maybe a = Nothing | Just a

, f :: a -> b F f :: Maybe a -> Maybe b. fmap. , ( ):


--          f                F f
--      /------\    /------------------\
fmap :: (a -> b) -> (Maybe a -> Maybe b)
fmap _ Nothing = Nothing
fmap f (Just x) = Just (f x)

, Maybe — . , , Functor. fmap, , ( — ):


class Functor f where
  fmap :: (a -> b) -> f a -> f b

— , , fmap . f a -> f b, , .



, , , .. , . : , - .


. , . , , — Haskell.


: upCase, , toWords, . toUpper words:


upCase :: String -> String
upCase = map toUpper

toWords :: String -> [String]
toWords = words

:


processString :: String -> [String]
processString = toWords . upCase

, . , processString "upCase toWords".


— , . -, , , -, , .


, a , .


newtype Writer a = Writer (a, String)

, Writer — , fmap:


instance Functor Writer where
  fmap f (Writer (x, s)) = Writer (f x, s)

upCase toWords , , "" Writer:


upCase :: String -> Writer String
upCase s = Writer (map toUpper s, "upCase ")

toWords :: String -> Writer [String]
toWords s = Writer (words s, "toWords ")

, , - . , b , , c c , :


compose :: (a -> Writer b) -> (b -> Writer c) -> (a -> Writer c)
compose f g = \x -> let Writer (y, s1) = f x
                        Writer (z, s2) = g y
                    in Writer (z, s1 ++ s2)

processString :


processString :: String -> [String]
processString = compose upCase toWords

. () a -> b a -> Writer b , a b. , .. a -> Writer a:


writerId :: a -> Writer a
writerId x = Writer (x, "")

, , Hask. , a b a -> b, a -> m b, .. "" - m. (embellished). m, Writer — .


C m. K, , C, .. ObK = ObC. a -> b K a -> m b C: HomK(a, b) = HomC(a, m b). , , K — C.


, , , . , m — . Haskell ( Hask):


class Monad m where
  --    
  (>=>)  :: (a -> m b) -> (b -> m c) -> (a -> m c)
  --  
  return :: a -> m a

>=>, "fish", : . , , — , , , . Writer — , compose — >=>, writerId — return.


>=> . , -. a, f, , , bind:


f >=> g = \a -> let mb = f a
                in (bind mb g)
  where
    bind :: m b -> (b -> m c) -> m c

bind b " " m , b m c. >=>. : m b -> (b -> m c) -> m c. , . "" Haskell >>=, bind, return:


class Monad m where
  (>>=)  :: m a -> (a -> m b) -> m b
  return :: a -> m a

, - b -> m c b, m b. , m, fmap, (a -> m b) -> m a -> m (m b). >>= m (m b) m b, "" , . join:


ma >>= g = join (fmap g ma)
  where
    join :: m (m a) -> m a

, Writer :


join :: Writer (Writer a) -> Writer a
join (Writer ((Writer (x, s2)), s1)) = Writer (x, s1 ++ s2)

Monad:


class Functor m => Monad m where
  join   :: m (m a) -> m a
  return :: a -> m a

, m . , fmap >>=:


fmap :: (a -> b) -> m a -> m b
fmap f ma = ma >>= (\a -> return (f a))


, "" .



(.. , ) .


(a -> [b]) -> (b -> [c]) -> (a -> [c]). :


(>=>) :: (a -> [b]) -> (b -> [c]) -> (a -> [c])
f >=> g = \x -> concat (map g (f x))

. a, , — f [b]. , b — g : map g (f x) :: [[c]]. , .


>>= :


(>>=) :: [a] -> (a -> [b]) -> [b]
xs >>= f = concat (map f xs)

return :: a -> [a]. :


return :: a -> [a]
return x = [x]

Monad:


instance Monad [] where
  xs >>= f = concat (map f xs)
  return x = [x]

, . , , . , — , ..



, , - .


, , Maybe. Just, — Nothing. , , :


(>=>) :: (a -> Maybe b) -> (b -> Maybe c) -> (a -> Maybe c)
f >=> g = \x -> case f x of
                  Just y  -> g y
                  Nothing -> Nothing

Monad Maybe:


instance Monad Maybe where
  (Just x) >>= f = f x
  Nothing  >>= f = Nothing
  return x = Just x

, . , - , , - . Either String a, : , . :


data Either a b = Left a | Right b

, . . :


type WithException a = Either String a

Maybe:


(>=>) :: (a -> WithException b) -> (b -> WithException c) -> (a -> WithException c)
f >=> g = \x -> case f x of
                  Right y -> g y
                  err     -> err

Monad :


instance Monad WithException where
  (Right x) >>= f = f x
  err >>= f = err
  return x = Right x


, , write-only , . a -> b , , . , , ( , ):


a -> s -> (b, s)

:


newtype State s a = State (s -> (a, s))

s , State s . runState:


runState :: State s a -> s -> (a, s)
runState (State f) s = f s

Functor:


instance Functor (State s) where
  fmap f state = State st'
    where
     st' prevState = let (a, newState) = runState state prevState
                     in (f a, newState)

, a b, , a -> State s b, State s — . , :


(>=>) :: (a -> State s b) -> (b -> State s c) -> (a -> State s c)
f >=> g = \x -> State (\s -> let (y, s') = runState (f x) s
                             in runState (g y) s')

Monad. , return, , -:


instance Monad (State s) where
  stateA >>= f = State (\s -> let (a, s') = runState stateA s
                              in runState (f a) s')
  return a = State (\s -> (a, s))

, . , Unit s , Unit -> State s s:


get :: Unit -> State s s
get _ = State (\s -> (s, s))

, Unit . , .


, , . , , , s Unit, s -> State s Unit:


put :: s -> State s Unit
put s = State (\_ -> ((), s))

, , /. , " " RealWorld, . RealWorld - , (, ). :


type IO a = State RealWorld a

IO — , Haskell, "". , . , , , -, .

Source: https://habr.com/ru/post/zh-CN445488/

More articles:


All Articles