😡 😏 🐭 神经量子态-用神经网络表示波函数 👍 👩🏼‍🤝‍👨🏽 🙇🏿

在本文中，我们将考虑神经网络在普通Boltzmann机器和有限Boltzmann机器中的不寻常应用，特别是在解决量子力学的两个复杂问题时-查找基态能量和逼近多体系统的波函数。

可以说，这是对2017年发表在《科学》上的一篇文章[2]的免费简化再现，以及随后的一些著作。尽管在我看来这很有趣，但我没有发现用俄语（只有英语版本的其中一种）流行的科学论述。

量子力学和深度学习中的基本概念

我想马上指出，这些定义都非常简化 。我为那些描述的问题是一片黑暗的森林带来了他们。

状态只是描述系统的一组物理量。例如，对于在太空中飞行的电子，将是其坐标和动量；对于晶格，将是位于其节点中的一组原子自旋。

系统的波动函数是系统状态的复杂函数。某个黑盒接受输入，例如一组旋转，但返回复数。对我们而言重要的波动函数的主要属性是其平方等于该状态的概率：

P s i （ s ） P s i （ s ）^{*} = P （ s ）

$\ Psi（s）\ Psi（s）^ * = P（s）$

将波函数的平方归一化为统一是合乎逻辑的（这也是重要的问题之一）。

希尔伯特空间 -在我们的例子中，这样的定义就足够了-系统所有可能状态的空间。例如，对于40个可以取值+1或-1的自旋系统，希尔伯特空间就是全部

2^{40}

$2 ^ {40}$ 可能的条件。对于可以取值的坐标

[- i n f t y ， + i n f t y]

$[-\ infty，+ \ infty]$ ，希尔伯特空间的维数是无限的。对于任何实际系统来说，希尔伯特空间的巨大维度是不允许解析地求解方程式的主要问题：在此过程中，整个希尔伯特空间将存在无法直接计算的积分/求和。一个奇怪的事实：对于宇宙的整个生命，您只能遇到希尔伯特空间中所有可能状态的一小部分。一张有关Tensor Networks [1]的图片很好地说明了这一点，该图片示意性地描述了整个希尔伯特空间以及从多项式的复杂性（空间，物体，粒子，自旋等的数量）的特性可以通过多项式满足的状态。

有限的Boltzmann机器 -如果难以解释，它是一种无向的图形概率模型，其局限性是一层的节点的概率与同一层的节点的条件独立性。如果以一种简单的方式，那么这是一个具有输入和一个隐藏层的神经网络。隐藏层中神经元的输出值可以是0或1。与通常的神经网络的区别在于，隐藏层神经元的输出是随机变量，其概率等于激活函数的值：

P_{i} （ 1 ） = s i g m a （ b_{i} + s u m_{j} W_{i j} s_{j} ）

$P_i（1）= \ sigma（b_i + \ sum_jW_ {ij} s_j）$

在哪里

s i g m a

$\ sigma$ - 乙状结肠激活功能，

b_{i}

$b_i$ -第i个神经元的偏移量，

W

$W$ -神经网络的权重，

s_{j}

$s_j$ -可见层。有限的Boltzmann机器属于所谓的“能量模型”，因为我们可以使用该机器的能量来表示机器特定状态的概率：

E （ v ， h ） = - a^{T} v - b^{T} h - v^{T} W h

$E（v，h）= -a ^ Tv-b ^ Th-v ^ TWh$

其中v和h是可见层和隐藏层， a和b是可见层和隐藏层的位移， W是权重。那么状态的概率可以用以下形式表示：

P （ v ， h ） = f r a c 1 Z e^{- E （ v ， h ）}

$P（v，h）= \ frac {1} {Z} e ^ {-E（v，h）}$

其中Z是归一化项，也称为统计和（必须使总概率等于1）。

引言

如今，深度学习领域的专家们认为，
玻尔兹曼机器（以下简称OMB）是一种过时的概念，实际上不适用于实际任务。然而，在2017年，《科学》杂志上发表了一篇文章 [2]，该文章显示了非常有效地使用OMB解决量子力学问题。

作者注意到了两个看似显而易见的重要事实，但以前从未有人想到过：

根据Tsybenko的通用定理，OMB是一个神经网络，理论上可以任意精确地近似任何函数（仍然有很多限制，但是您可以跳过它们）。
OMB是一个系统，其每个状态的概率是神经网络的输入（可见层），权重和位移的函数。

作者还进一步说：让我们的系统完全由波动函数来描述，波动函数是OMB能量的根，而OMB输入是我们系统状态的特征（坐标，自旋等）：

P s i （ s ） = f r a c 1 Z s q r t e^{E （ s ， h ）}

$\ Psi（s）= \ frac {1} {Z} \ sqrt {e ^ {E（s，h）}}$

其中s是状态的特征（例如，背面），h是OMB隐藏层的输出，E是OMB的能量，Z是归一化常数（统计和）。

就是这样，《科学》杂志上的文章已经准备好了，只剩下了一些小细节。例如，由于希尔伯特空间的巨大尺寸，有必要解决不可计算的分区函数的问题。齐申科的定理告诉我们，神经网络可以近似任何函数，但根本没有说明如何为此找到合适的网络权重和偏移量。好了，和往常一样，乐趣从这里开始。

模型训练

现在对原始方法进行了很多修改，但是我将只考虑原始文章[2]中的方法。

挑战赛

在我们的案例中，训练任务如下：找到波动函数的近似值，该近似值将使能量最小的状态最可能出现。这在直观上很清楚：波动函数为我们提供了状态的概率，即哈密顿量的特征值（能量算符，或更简单的能量，这种理解在本文的框架中足够了），因为波动函数就是能量。一切都很简单。

实际上，我们将努力优化另一个量，即所谓的局部能量，该量始终大于或等于基态的能量：

E_{l o c} （ s i g m a ） = R e s u m_{s i g m a s i g m a^{'}} H_{s i g m a s i g m a^{'}} f r a c P s i （ s i g m a^{'} ） P s i （ s i g m a ）

$E_ {loc}（\ sigma）= Re \ sum _ {\ sigma \ sigma'} H _ {\ sigma \ sigma'} \ frac {\ Psi（\ sigma'）} {\ Psi（\ sigma）}$

在这里

s i g m a

$\ sigma$ 是我们的条件

s i g m a^{'}

$\ sigma'$ -希尔伯特空间的所有可能状态（实际上，我们将考虑一个更近似的值），

H_{s i g m a s i g m a^{'}}

$H _ {\ sigma \ sigma'}$ 是哈密顿量的矩阵元素。很大程度上取决于特定的哈密顿量，例如，对于伊辛模型，这仅仅是

f （ s i g m a ）

$f（\ sigma）$ 如果

s i g m a = s i g m a^{'}

$\ sigma = \ sigma'$ 和

- c o n s t

$-const$ 在所有其他情况下。现在不要在这里停下来。重要的是可以为各种流行的汉密尔顿主义者找到这些元素。

优化过程

取样方式

原始文章中方法的重要部分是采样过程。使用了Metropolis-Hastings算法的修改版本。底线是：

我们从随机状态开始。
我们将随机选择的旋转的符号更改为相反的符号（对于坐标，还存在其他修改，但它们也存在）。
概率等于 $P（\ sigma'| \ sigma）= \大| {\ frac {\ Psi（\ sigma'）} {\ Psi（\ sigma）} \ Big | ^ 2$ ，移至新状态。
重复N次。

结果，我们获得了根据波动函数给出的分布选择的一组随机状态。您可以计算每种状态下的能量值以及能量的数学期望

m a t h b b E （ E_{l o c} ）

$\ mathbb {E}（E_ {loc}）$ 。

可以证明，能量梯度的估计值（更准确地说，是哈密顿量的期望值）等于：

G_{k} （ x ） = 2 * （ E_{l o c} （ x ） - m a t h b b E （ E_{l o c} ） ） * D_{k}^{*} （ x ）

$G_k（x）= 2 *（E_ {loc}（x）-\ mathbb {E}（E_ {loc}））* D ^ * _ k（x）$

结论

这摘自G.Carleo在2017年为量子科学和量子技术高级学院的演讲。 Youtube上有条目。

表示：

D_{k}^{*} （ x ） = f r a c p a r t i a l_{p_{k}} P s i （ x ） P s i （ x ）

$D ^ * _ k（x）= \ frac {\ partial_ {p_k} \ Psi（x）} {\ Psi（x）}$

然后：

p a r t i a l_{p_{k}} m a t h b b E （ H ） =

$\ partial_ {p_k} \ mathbb {E}（H）=$

\部 分 f r a c s u m_{x x^{'}} P s i^{*} （ x ） H_{x x^{'}} P s i （ x^{'} ） s u m_{x} | P s i （ x ） |^{2} =

$\部分\ frac {\ sum_ {xx'} \ Psi ^ *（x）H_ {xx'} \ Psi（x'）} {\ sum_x | \ Psi（x）| ^ 2} =$

f r a c s u m_{x x^{'}} P s i^{*} （ x ） H_{x x^{'}} D_{k} （ x^{'} ） P s i （ x^{'} ） s u m_{x} | P s i （ x ） |^{2} + f r a c s u m_{x x^{'}} P s i^{*} （ x ） D_{k}^{*} （ x ） H_{x x^{'}} P s i （ x^{'} ） s u m_{x} | P s i （ x ） |^{2} -

$\ frac {\ sum_ {xx'} \ Psi ^ *（x）H_ {xx'} D_k（x'）\ Psi（x'）} {\ sum_x | \ Psi（x）| ^ 2} + \ frac {\ sum_ {xx'} \ Psi ^ *（x）D_k ^ *（x）H_ {xx'} \ Psi（x'）} {\ sum_x | \ Psi（x）| ^ 2}-$

f r a c s u m_{x x^{'}} P s i^{*} （ x ） H_{x x^{'}} P s i （ x^{'} ） s u m_{x} | P s i （ x ） |^{2} f r a c s u m_{x} | P s i （ x ） |^{2} （ D_{k} （ x ） - D_{k}^{*} （ x ） ） s u m_{x} | P s i （ x ） |^{2} =

$\ frac {\ sum_ {xx'} \ Psi ^ *（x）H_ {xx'} \ Psi（x'）} {\ sum_x | \ Psi（x）| ^ 2} \ frac {\ sum_x | \ Psi （x）| ^ 2（D_k（x）-D ^ * _ k（x））} {\ sum_x | \ Psi（x）| ^ 2} =$

f r a c s u m_{x x^{'}} f r a c P s i^{*} （ x ） P s i^{*} （ x^{'} ） H_{x x^{'}} D_{k} （ x^{'} ） | P s i （ x^{'} ） |^{2} + s u m_{x x^{'}} | P s i （ x ） |^{2} H_{x x^{'}} D_{k}^{*} （ x^{'} ） f r a c P s i （ x^{'} ） P s i （ x ） s u m_{x} | P s i （ x ） |^{2} -

$\ frac {\ sum_ {xx'} \ frac {\ Psi ^ *（x）} {\ Psi ^ *（x'）} H_ {xx'} D_k（x'）| \ Psi（x'）| ^ 2 + \ sum_ {xx'} | \ Psi（x）| ^ 2H_ {xx'} D ^ * _ k（x'）\ frac {\ Psi（x'）} {\ Psi（x）}} {\ sum_x | \ Psi（x）| ^ 2}-$

m a t h b b E （ H ） f r a c s u m_{x} | P s i （ x ） |^{2} （ D_{k} （ x ） + D_{k}^{*} （ x ） ） s u m_{x} | P s i （ x ） |^{2} \大 约

$\ mathbb {E}（H）\ frac {\ sum_x | \ Psi（x）| ^ 2（D_k（x）+ D ^ * _ k（x））} {\ sum_x | \ Psi（x）| ^ 2 } \大约$

m a t h b b E （ E_{l o c} D_{k}^{*} ） - m a t h b b E （ E_{l o c} ） m a t h b b E （ D_{k}^{*} ） + C

$\ mathbb {E}（E_ {loc} D ^ * _ k）-\ mathbb {E}（E_ {loc}）\ mathbb {E}（D ^ * _ k）+ C$

然后我们只解决优化问题：

我们从OMB采样状态。
我们计算每个状态的能量。
估计渐变。
我们更新OMB的权重。

结果，能量梯度趋于零，能量值降低，Metropolis-Hastings过程中独特的新状态数也减少，因为通过从真波函数采样，我们几乎总是获得基态。凭直觉，这似乎是合乎逻辑的。

在原始工作中，对于小型系统，获得了基态能量的值，非常接近于通过分析获得的精确值。与众所周知的方法进行比较以求出基态的能量，NQS获得了胜利，特别是考虑到与已知方法相比NQS的计算复杂度较低。

NetKet-来自“发明家”方法的图书馆

原始文章[2]的作者之一与他的团队一起开发了出色的NetKet库[3]，该库包含一个非常优化（在我看来）的C内核以及可与高级抽象配合使用的Python API。

该库可以通过pip安装。 Windows 10用户将必须使用Windows的Linux子系统。

让我们考虑使用该库作为示例，以40个旋转的链为例，取值+ -1 / 2。我们将考虑海森堡模型，该模型考虑了邻近的相互作用。

NetKet具有出色的文档，可让您快速确定操作方法。有许多内置模型（后背，玻色子，伊辛，海森堡模型等），并且可以自己完整描述模型。

计数说明

所有模型均以图形表示。对于我们的链，具有一维和周期性边界条件的内置Hypercube模型是合适的：

import netket as nk graph = nk.graph.Hypercube(length=40, n_dim=1, pbc=True)

希尔伯特空间的描述

我们的希尔伯特空间非常简单-所有自旋可以取+1/2或-1/2的值。对于这种情况，内置的自旋模型是合适的：

 hilbert = nk.hilbert.Spin(graph=graph, s=0.5)

哈密顿量的描述

正如我已经写过的，在我们的例子中，哈密顿量是海森堡哈密顿量，其中有一个内置运算符：

 hamiltonian = nk.operator.Heisenberg(hilbert=hilbert)

RBM的描述

在NetKet中，您可以使用现成的RBM实现进行旋转-这只是我们的例子。但通常有很多汽车，您可以尝试不同的汽车。

 nk.machine.RbmSpin(hilbert=hilbert, alpha=4) machine.init_random_parameters(seed=42, sigma=0.01)

这里的alpha是隐藏层中神经元的密度。对于40个可见的和alpha 4的神经元，将有160个，还有另一种直接通过数字指示的方法。第二条命令从以下位置随机初始化权重

N （ 0 ， s i g m a ）

$N（0，\ sigma）$ 。在我们的情况下，sigma为0.01。

萨姆勒

采样器是一个对象，该对象将由分布中的样本返回给我们，该分布由希尔伯特空间上的波动函数给出。我们将使用上面描述的Metropolis-Hastings算法，并对其进行了修改：

 sampler = nk.sampler.MetropolisExchangePt( machine=machine, graph=graph, d_max=1, n_replicas=12 )

确切地说，采样器是一种比我上面描述的算法更棘手的算法。在这里，我们同时并行检查多达12个选项以选择下一个点。但是一般来说，原理是相同的。

优化器

这描述了将用于更新模型权重的优化器。根据在更熟悉的领域使用神经网络的个人经验，最好和最可靠的选择是良好的老式随机梯度下降，并有一点点时间（此处详细介绍）：

 opt = nk.optimizer.Momentum(learning_rate=1e-2, beta=0.9)

培训课程

NetKet在没有老师（我们的案例）和没有老师的情况下都接受了培训（例如，所谓的“量子层析成像”，但这是另一篇文章的主题）。我们仅描述“老师”，仅此而已：

 vc = nk.variational.Vmc( hamiltonian=hamiltonian, sampler=sampler, optimizer=opt, n_samples=1000, use_iterative=True )

变异蒙特卡洛表示我们如何评估所优化函数的梯度。 n_smaples是采样器返回的分布中的样本大小。

结果

我们将如下运行模型：

 vc.run(output_prefix=output, n_iter=1000, save_params_every=10)

该库是使用OpenMPI构建的，脚本需要像这样运行： mpirun -n 12 python Main.py （12是内核数）。

我收到的结果如下：

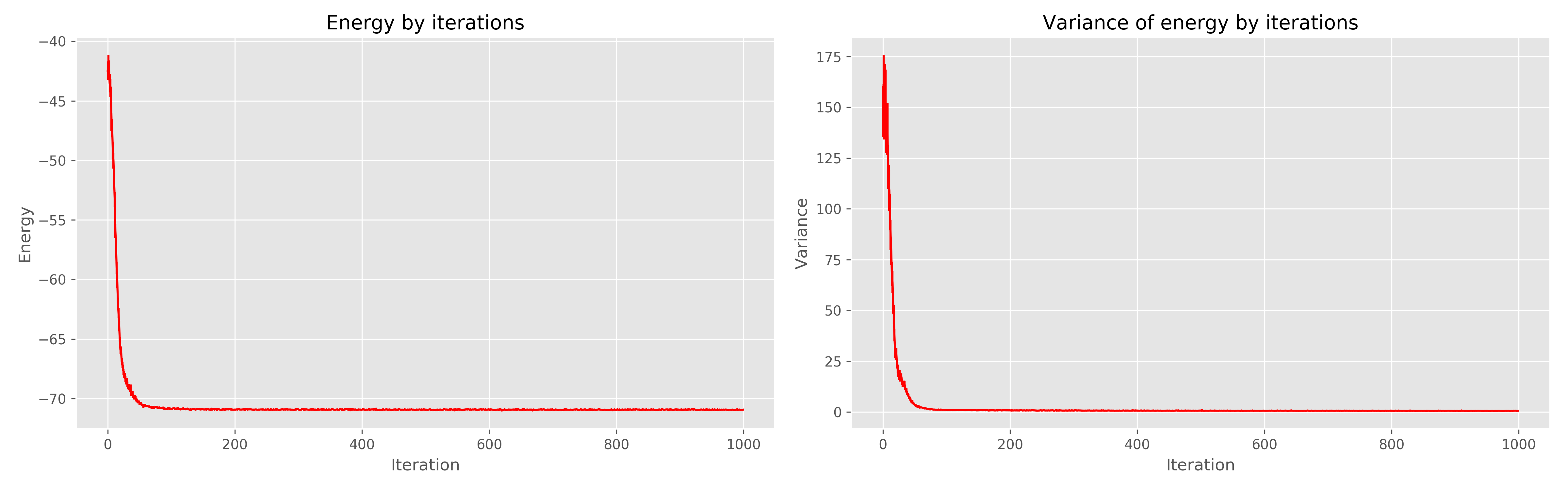
左边是学习时代的能量图，右边是学习时代的能量散布。
可以看出，1000个时代显然是多余的，而300个时代就已经足够了，总的来说，它的工作非常酷，并且收敛很快。

文学作品

OrúsR.张量网络的实用介绍：矩阵乘积状态和投影的纠缠对状态//物理学年鉴。 -2014年-T.349。-S.117-158。
Carleo G.，Troyer M.用人工神经网络解决量子多体问题//科学。 -2017.-T. 355.-否 6325.-S.602-606。
www.netket.org

神经量子态-用神经网络表示波函数

引言