在量子化学方面的Muon催化。 第二部分：电子与 介子化学键

Mnogabukaff认为，量子化学考虑了μ子催化的原理：μ子到底如何降低所需等离子体的温度。 分两部分（第一部分可以在此处阅读）。

第二部分的本质很简单：μ子比电子重，因此它提供了更强的化学键和更接近的原子核，从而降低了引发热核反应所需的等离子体温度。

但是，那些希望查看分子式，图表并看到应用于最简单（准）分子的量子化学概念实质的人，受到了欢迎。

引言

在第一部分（请参阅此处 ）中，我们检查了氢原子之间的差异 $$$\ mathrm {H} ^ \ cdot = \ mathrm {p ^ + e ^-}$ 从笨重的介子对应 $$$\ mathrm {p} ^ + \ mu ^-$ ：在第二种情况下，μ子将被更牢固地束缚，并与质子距离更近。 同时，我们研究了这里需要的一些重要事物（轨道的形式和单位的原子系统）。

在第二部分（即此处）中，我们将尝试理解为什么点燃热核反应所需的等离子体温度降低，降低程度和降低程度。 我们感兴趣的反应是：

$$

$$\ mathrm {{} ^ nH + {} ^ m H \ rightarrow} \ \ text {新内核+能量}$$

其中n，m = 1,2,3分别对应于质子，氘和tri。 这些核自然会带正电荷，因此，如果您试图使其更靠近，它们将根据库仑定律（请参阅上一部分 ）开始排斥，这是防止聚变反应发生的非常大的障碍。 顺便说一句，在核衰变反应的情况下，这种排斥作用是相反的，因为在与共同核分离之后，彼此排斥的碎片获得了额外的动能，而正是这种能量在核电站中被加热。

为了克服这种库仑势垒，需要提高等离子体温度（ T ），正如大家从MKT的学校课程中所记得的那样，通过以下公式将其与等离子体中的平均粒子速度（ v ）相关联

$$

$$mv ^ 2 = 3k_ \ mathrm {B} T$$

其中m是粒子的质量，并且 $$$k_ \ mathrm {B}$ - 玻耳兹曼常数 。

但是，让我们想象一下，我们已经将两个氢核组合成一个特定的粒子，它们已经位于附近，因此对它们的其余障碍已经很小。 然后，我们需要显着加速这些粒子（请阅读：我们需要更低的温度），以便将它们组合成新的事物。 而这样的作用应该起到中间离子的作用 $$$（\ mathrm {{} ^ nH} \ mu ^-\ mathrm {{} ^ mH}）^ +$ 氢分子离子的类似物 $$$\ mathrm {H} _2 ^ + =（\ mathrm {He ^ -H}）^ +$ 。
在检查了这两个粒子之间的差异之后，我们将认识到μ子在降低热核聚变的着火温度方面的有效性。

牛奶 MO LKAO方法

因此，我们有一个分子系统，该系统由2个带电荷+ e的氢核（一个电子电荷模）和一个带电荷e的粒子（电子或介子）组成。 我们的系统在与其他粒子碰撞之前一直处于隔离状态，因此可以将其能量分解为以下组成部分：

$$

$$E = T（\ mathrm {H} _1）+ T（\ mathrm {H} _2）+ \括号{T（\ mathrm {e} ^-/ \ mu ^-）+ V（\ mathrm {H_1 \ text {from} H_2}）+ V（\ mathrm {\ mathrm {e} ^-/ \ mu ^-\ text {} \ mathrm {H} _1}）+ V（\ mathrm {\ mathrm {e} ^- / \ mu ^-\文字{k} \ mathrm {H} _2}）} _ {E_ \ mathrm {e}}$$

前两个词（ $$$T（\ mathrm {H} _1）$ 和 $$$T（\ mathrm {H} _2）$ ）是氢核的动能，第三项（ $$$T（\ mathrm {e} ^-/ \ mu ^-）$ ）是负粒子（电子或介子）的动能，第四项 $$$V（\ mathrm {H_1 \文字{from} H_2}）$ 是氢相互之间排斥氢的库仑能量，其余两个是电子/介子对每个质子的库仑​​吸引力。 在一般情况下，这是一个三体问题，只是一个量子问题。 自然地，解决额头上的问题非常困难。 但是，幸运的是，核比电子重至少1800倍，比介子重10倍，因此它们的运动明显比小的负粒子慢。 因此，您首先可以依次解决问题：首先，找到与原子核运动无关的运动能量，即 $$$E_ \ mathrm {e}$ 然后充满能量。 看起来像这样。

1. 选择氢原子相对于彼此的排列，这决定了氢原子之间以及与电子/介子之间的库仑相互作用。 库仑势 $$$V（R）= k \ frac {q_1q_2} {R}$ 仅取决于粒子电荷 $$$q_i$ 以及它们之间的距离，因此对于所有氢同位素而言，该值都将相同。 此外，解决了这些原子核领域中电子/介子的运动问题。 这是一个身体的任务。
2. 这些能量 $$$E_ \ mathrm {e}$ 计算原子核相对于彼此的所有可能排列，这将是原子核运动的有效势能。 在我们的案例中，我们需要计算彼此之间不同距离处的能量，因此一对原子核的电势始终是一维的。 好吧，那么我们只需要解决两个氢同位素相对于彼此运动的两体问题。

显然，与我们有关的问题的根源是计算原子核领域中的电子/μ子能 $$$E_ \ mathrm {e}$ 。 实际上，这是化学键：在某些位置将核保持在一起的特定电势。 而寻找化学键能的这一任务是量子化学中的主要任务。

不幸的是，介子和电子都是量子粒子，因此，为了找到这种能量，我们必须求助于量子力学方法。 实际上，我们在两个相同原子核场中的电子/介子运动问题已得到明确解决（请参见此处 ），但是该解决方案非常复杂，其结果不像氢原子那样清晰。 因此，我们将尝试分解适用于任何系统的其他近似方法。 这就是所谓的 分子轨道法作为原子轨道或MO LKAO的线性组合。

让我们仔细看一下氢原子核领域中电子/介子运动的薛定ding方程：

$$

$$\ hat {H} \ psi = \ underbrace {\ left（\ overbrace {-\ frac {1} {2m}（\ frac {\部分^ 2} {\部分x ^ 2} + \ frac {\部分^ 2} {\部分y ^ 2} + \ frac {\部分^ 2} {\部分z ^ 2}）} ^ {\帽子{T}} + \大括号{-\ frac {1} {R_1}} ^ {\ hat {V} _1} + \ overbrace {-\ frac {1} {R_2}} ^ {\ hat {V} _2} + \ overbrace {\ frac {1} {R}} ^ {\ hat {V } _ \ mathrm {HH}} \ right）} _ {\ hat {H}} \ psi = E \ psi$$

该方程式是用原子单位制写的（请参见前面的PS ），因此，氢核的电荷和电子/μ子的电荷分别为+1和-1，电子质量为m = 1，且μ= 207。

如果仔细看一看，您会发现在哈密顿量中，您可以选择与负粒子仅围绕一个原子核运动的纯粹运动相关的片段，这仅是氢原子的哈密顿量，这可以通过两种方式完成：

$$

$$\ hat {H} =（\ overbrace {\ hat {T} + \ hat {V} _1} ^ {\ hat {H} _ {1}} + \ hat {V} _2 + \ hat {V} _ \ mathrm {HH}）=（\ overbrace {\ hat {T} + \ hat {V} _2} ^ {\ hat {H} _ {2}} + \ hat {V} _1 + \ hat {V} _ \ mathrm {HH}）$$

类氢原子的哈密顿量之外（ $$$\ hat {H} _i，\ i = $ 1.$ ），我们总是有2个块：电子/介子与另一个原子核相互作用的能量（ $$$\帽子{V} _j$ ）和核排斥能（ $$$\帽子{V} _ \ mathrm {HH}$ ） 它们中的第二个根本不影响电子的运动-只是一定程度的能量转移，但是电子与另一个原子核的相互作用很重要。
我们可以想象，在任何时刻，我们的粒子仅绕一个原子核旋转，而与第二个原子核的相互作用只是一个校正。 作为绕一个原子核旋转的一种方法，我们可以假定电子/介子处于基态（1s），其波函数从上一部分中为我们所熟知：

$$

$$| 1s \ rangle = \ frac {1} {\ sqrt {\ pi}} \ exp \ left（-\ frac {R} {R_1} \ right）$$

在哪里 $$$R_1$ 是粒子的玻尔半径。 在电子的情况下 $$$R_1 = 1$ 硼（它是电子的玻尔半径，大约等于0.5埃），在μ子的情况下 $$$R_1 = \ frac {1} {m_ \ mu} \大约\ frac {1} {207}$ 。
为了以某种方式近似2核场中的电子/μ子波函数，我们可以尝试采用以下表示形式：

$$

$$\ psi \大约c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle$$

然后用我们求解一个复杂的偏微分方程的问题简化为寻找2个未知系数c ₁和c ₂ 。 这是一个非常分子的轨道，以系数（科学的线性组合）原子1s轨道的总和表示。

自然，我们需要这些参数的方程式。 如果在Schrödinger方程中代入该近似值，则得到它非常简单 $$$\帽子{H} \ psi = E \ psi$ ：

$$

$$\ hat {H}（c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle）= c_1 \ hat {H} | 1s_1 \ rangle + c_2 \ hat {H} | 1s_2 \ rangle = E（c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle）= c_1 E | 1s_1 \ rangle + c_2 E | 1s_2 \ rangle$$

实际上，我们希望这个比率在任何地方都可以满足，因此我们可以通过某种方式计算出这一切的平均值。 我们将左边的等式乘以 $$$<1s_1 |$ 和 $$$<1s_2 |$ 并整合所有坐标。 结果，我们获得了一个由2个线性方程组成的系统，其中必须找到系数c ₁ ， c ₂和能量E ：

$$

$$\ begin {pmatrix} \ langle 1s_1 | \ hat {H} | 1s_1 \ rangle＆\ langle 1s_1 | \ hat {H} | 1s_2 \ rangle \\ \ langle 1s_2 | \ hat {H} | 1s_1 \ rangle＆\ langle 1s_2 | \帽子{H} | 1s_2 \ rangle \\ \结束{pmatrix} \开始{pmatrix} c_1 \\ c_2 \ end {pmatrix} = E \ begin {pmatrix} \ langle 1s_1 | 1s_1 \ rangle＆\ langle 1s_1 | 1s_2 \ rangle \\ \ langle 1s_2 | 1s_1 \ rangle＆\ langle 1s_2 | 1s_2 \ rangle \\ \ end {pmatrix} \ begin {pmatrix} c_1 \\ c_2 \ end {pmatrix}$$

学习过线性代数的任何人都会认识到广义特征向量-特征值问题。 在解决它之前，我们将分析两个矩阵（现有的tuta）的元素相等（并同时用一个字母引入它们的简称）。

• 让我们从最简单的开始： $$$\ langle 1s_1 | 1s_1 \ rangle = \ langle 1s_2 | 1s_2 \ rangle = 1$ -这是波函数的归一化，正如我们回想的，在某处找到电子/μ子的总概率至少为1。
• $$$\ langle 1s_1 | 1s_2 \ rangle = \ langle 1s_2 | 1s_1 \ rangle = S$ -这就是所谓的 重叠积分，显示1s电子云如何与每个原子重叠。
• $$$\ langle 1s_1 | \ hat {H} | 1s_1 \ rangle = \ langle 1s_2 | \ hat {H} | 1s_2 \ rangle = \ alpha$ 。 该积分包括几个部分：
  

  $$

  $$\ langle 1s_1 | \ hat {H} | 1s_1 \ rangle = \底线{\ langle 1s_1 | \ hat {H} _1 | 1s_1 \ rangle} _ {-\ frac {m} {2}} + \ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle + \ frac {1} {R}$$
  
  
• $$$\ langle 1s_1 | \ hat {H} | 1s_2 \ rangle = \ langle 1s_2 | \ hat {H} | 1s_1 \ rangle = \ beta$ 。 这里是类似的：
  

  $$

  $$\ langle 1s_2 | \ hat {H} | 1s_1 \ rangle = \ underbrace {\ langle 1s_2 | \ overbrace {\ hat {H} _1 | 1s_1 \ rangle} ^ {-\ frac {m} {2} | 1s_1 \ rangle}} {{\ frac {m} {2} S} + \ langle 1s_2 | \帽子{V} _2 | 1s_1 \ rangle + \ frac {S} {R}$$
  
  即 类氢原子和核间斥力的能量，由重叠积分（第一项和最后一项）定标，以及电子/介子从一个原子跳到另一个原子的能量。
  

让我们从重写为的方程式中找到类氢离子能量的表达式

$$

$$\开始{pmatrix} \ alpha＆\ beta \\ \ beta＆\ alpha \结束{pmatrix} \开始{pmatrix} s_1 \\ c_2 \结束{pmatrix} = E \开始{pmatrix} 1＆S \\ S ＆1 \结束{pmatrix} \开始{pmatrix} c_1 \\ c_2 \结束{pmatrix}$$

要找到能量，您需要解方程：

$$

$$\ det \ begin {pmatrix} \ alpha -E＆\ beta -ES \\ \ beta-ES＆\ alpha -E \ end {pmatrix} =（\ alpha -E）^ 2-（\ beta-ES）^ 2 = 0$$

其中“ det”表示行列式（矩阵的行列式，俄语）。

关于E的该二次方程式的解是：

$$

$$E_ \ pm = \ frac {\ alpha \ pm \ beta} {1 \ pm S} =-\ frac {m} {2} + \ frac {1} {R} + \ frac {\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle \ pm \ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle} {1 \ pm S}$$

第一块显然是原子的能量，第二块是核之间的排斥力，即阻止热核反应点火的同一个库仑势垒，必须处​​理最后一个复杂的结构。

如果我们放弃核间排斥力，而核间排斥力只是电子/μ子能级的参考点，我们会得到两个带能态

$$

$$\ epsilon_ \ pm =-\ frac {m} {2} + \ frac {\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle \ pm \ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle} {1 \ pm S}$$

由于两个波函数 $$$| 1s_1 \ rangle$ 和 $$$| 1s_2 \ rangle$ -正面，以及 $$$\帽子{V} _i <0$ （因为负粒子总是被吸引到正粒子），然后 $$$\ epsilon_ + <-\ frac {m} {2}$ （单个原子的能量），以及 $$$\ epsilon _->-\ frac {m} {2}$ ，即 我们得到了分子轨道的标准图：



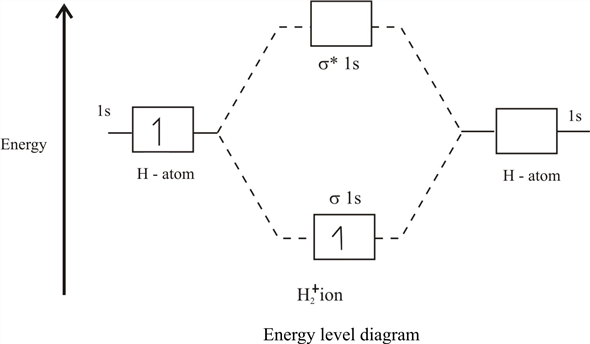
较低轨道的能量 $$$E _ +$ 称为绑定，顶部（具有能量 $$$E _-$ ）-防粘连或松动。 结果，如果一个电子/介子坐在较低的分子轨道上，那么它从绕2个核飞行而不是绕1个核中受益，随着它的运动，它降低了系统的总能量。 这是一个非常神奇的化学键，可以屏蔽核之间的排斥，使核彼此相邻相当长的一段时间。

在这里，必须计算化学键的积分，以了解氢核的允许距离。 实际上，所有这三个受欢迎的积分都是经过分析计算的，但它非常痔疮且复杂（任何感兴趣的人，请参阅Flary的《量子化学》一书的第9章）。 因此，我们将采用一种更简单的方法，并使用蒙特卡洛方法以数值方式计算这些积分。

都市法

在热核能的文字中，我向她的祖父表示敬意是非常合乎逻辑的：军事原子，更具体地说是曼哈顿计划 。 正是从他那里产生了蒙特卡罗方法，尤其是Metropolis算法 ，其中的作者之一Edward Edwarder是“氢弹之父”（即在Envetok环礁上发起热核聚变的人）。


通常，我们将分析该方法的本质。 它旨在用于统计力学的任务。 其中的主要分布是Boltzmann分布：在特定状态下检测到系统的概率为 $$$\ exp（-\ beta E）$ ， $$$\ beta ^ {-1} = k_ \ mathrm {B} T$ 。 并且系统在热力学平衡中某些参数A的观测值等于积分

$$

$$\ langle A \ rangle = \ frac {1} {Z} \ int A（q）\ exp（-\ beta E（q））dq$$

其中q是参数化系统状态的坐标（例如，粒子的坐标/矩）， Z是归一化因子，称为分区函数：

$$

$$Z = \ int \ exp（-\ beta E（q））dq$$

如果系统中有很多粒子，那么不计算额头中的任何积分都是完全不现实的。 如果系统的确实存在可能发生概率的状态，则朴素的蒙特卡洛方法（其中我们仅选择一堆随机q坐标）也不会给出任何有意义的信息 $$$\ exp（-\ beta E）$ 明显非零，很少。 正是在这种情况下，我们需要按重要性进行采样，在这种情况下，我们允许算法仅对状态空间中足够可能的位置进行采样。

Metropolis算法如下所示。

1. 启动仿真时，我们在配置空间中选择一些起始近似值 $$$\ mathbf {q} ^ {（0）}$ 和一些最大可能增量的向量 $$$\ delta \ mathbf {q}$ 。 首先，我们计算系统的能量 $$$E ^ {{（0）} = E（\ mathbf {q} ^ {{0）}）$ （已读-概率 $$$p = \ exp（-\ beta E ^ {（0）}）$ ）
2. 第n步的新配置如下。
   
   1. 计算试用配置的能量 $$$E_ \ mathrm {trial} = E（\ mathbf {q} _ \ mathrm {trial}）$ （即概率 $$$p_ \ mathrm {trial} = \ exp（-\ beta E_ \ mathrm {trial}）$ ）
   2. 然后我们比较旧的概率 $$$p ^ {（n）}$ 试用 $$$p_ \ mathrm {trial}$
      
      
      • 如果新配置具有更大或相同的可能性（ $$$\ frac {p_ \ mathrm {trial}} {p ^ {{n}}} \ geq 1$ ），或者等效地，新点的能量低于或等于旧点的能量（ $$$E_ \ mathrm {trial} \ leq E ^ {（n）}$ ），然后接受新点，系统进入该点（ $$$q ^ {（n + 1）} = q_ \ mathrm {trial}$ ），
      • 如果试验配置的能量较高（ $$$E_ \ mathrm {trial}> E ^ {（n）}$ ），相当于 $$$\ frac {p_ \ mathrm {trial}} {p ^ {（n）}} <1$ ，那么在这种情况下，我们生成一个随机数 $$$P \ in [0; 1）$ 从均匀分布中提取出来，并将其与概率比（即转移概率）进行比较。 如果 $$$P <\ frac {p_ \ mathrm {trial}} {p ^ {（n）}}$ ，那么我们接受一个新观点，如果不接受（ $$$P \ geq \ frac {p_ \ mathrm {trial}} {p ^ {{n}}}$ ），然后我们拒绝，系统仍保持旧配置（ $$$q ^ {（n + 1）} = q ^ {（n）}$ ）...
      
      
   
   
3. 根据上述算法采取许多步骤，我们对系统配置可能的空间中的重要部分（即非常重要的部分）进行了采样。 我们感兴趣的积分由以下公式计算：
   $$$\ langle A \ rangle = \ frac {1} {Z} \ int A（\ mathbf {q}）\ exp（-\ beta E（\ mathbf {q}））d \ mathbf {q} = \ frac { 1} {N} \ sum_ {n = 0} ^ {N} A（\ mathbf {q} ^ {{n}}）$
   

这就是Metropolis算法的工作方式。

现在，有必要使它适应于我们感兴趣的3个积分的计算。 让我们更详细地了解它们。

• $$$S（R）= \ langle 1s_2 | 1s_1 \ rangle = \ int \极限_ {-\ infty} ^ {+ \ infty} \ int \极限_ {-\ infty} ^ {+ \ infty} \ int \极限_ {- \ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp（-m \ underbrace {| \ mathbf {r}-\ mathbf {r} _2 | } _ {R_2}）} _ {1s_2}} ^ {A（\ mathbf {r}）} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp（-m \底线{| \ mathbf {r}-\ mathbf {r} _1 |} _ {R_1}）} _ {1s_1}} ^ {p（\ mathbf {r}）} dx dy dz$ 在哪里 $$$\ mathbf {r} =（x，y，z）^ \ mathbf {T}$ -电子/μ子的坐标， $$$\ mathbf {r} _i =（x_i，y_i，z_i）^ \ mathbf {T}$ 是氢核的坐标，并且 $$$R_i = | \ mathbf {r}-\ mathbf {r} _i | = \ sqrt {（x-x_i）^ 2 +（y-y_i）^ 2 +（z-z_i）^ 2}$ -正负粒子之间的距离，
  
• $$$\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle =-\ int \极限_ {-\ infty} ^ {+ \ infty} \ int \极限_ {-\ infty} ^ {+ \ infty} \ int \限制_ {-\ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp（-mR_1）} _ {1s_1} \ frac {1} {R_2} } ^ {A（\ mathbf {r}）} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp（-mR_1）} _ {1s_1}} ^ {p（\ mathbf {r}）} dxdydz$
• $$$\ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle =-\ int \极限_ {-\ infty} ^ {+ \ infty} \ int \极限_ {-\ infty} ^ {+ \ infty} \ int \限制_ {-\ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp（-mR_2）} _ {1s_2} \ frac {1} {R_1} } ^ {A（\ mathbf {r}）} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp（-mR_1）} _ {1s_1}} ^ {p（\ mathbf {r}）} dxdydz$

可以看出，如果我们针对概率p计算原子之一的1s函数，


那么在积分符号下的所有其他函数（第二个波函数以及在3种情况中的2种中，电子/μ子吸引原子核的电势）将是一个其平均值被计算的函数。 与通过Metropolis方法进行的通常计算相比，唯一要做的是拉直积分的归一化。 事实是标准规范化将继续进行

$$

$$Z = \ int \极限_ {-\ infty} ^ {+ \ infty} \ int \极限_ {-\ infty} ^ {+ \ infty} \ int \极限_ {-\ infty} ^ {+ \ infty} \ exp （-m R）dx dy dz = 4 \ pi \ int \极限_ {0} ^ {+ \ infty} \ exp（-m R）R ^ 2 dR = \ frac {8 \ pi} {m ^ 3}$$

我们需要规范化 $$$\ sqrt {\ langle 1s_1 | 1s_1 \ rangle}$ 在哪里

$$

$$\ langle 1s_1 | 1s_1 \ rangle = \ int \极限_ {-\ infty} ^ {+ \ infty} \ int \极限_ {-\ infty} ^ {+ \ infty} \ int \极限_ {-\ infty} ^ {+ \ infty} \ exp（-2 m R）dx dy dz = 4 \ pi \ int \ limits_ {0} ^ {+ \ infty} \ exp（-2m R）R ^ 2 dR = \ frac {\ pi} {m ^ 3}$$

这意味着根据都市计算的每个积分都需要乘以一个因子

$$

$$\ frac {Z} {\ sqrt {\ langle 1s_1 | 1s_1 \ rangle}} = 8 \ sqrt {\ frac {\ pi} {m ^ 3}}$$

这可以已经以某种脚本的形式进行了安排，例如在Python中（例如，下面的代码）。


使用这种计算，我们最终可以比较氢离子中的势能 $$$\ mathrm {H} _2 ^ +$ 和它的μon对应物。

$$$\ mathrm {H_2 ^ + = p ^ + e ^-p ^ +}$ 与 $$$\ mathrm {p ^ + \ mu ^-p ^ +}$

因此，借助脚本，我们可以计算由电子和介子束缚的氢核接近的势能表面。 作为能量参考点，我们将原子彼此无限稀释（即， $$$-m / 2$ ，它等于原子核之间距离的电势 $$$R = + \ infty$ ）

对于电子，接近最小值的电势如下所示：



最小值发生在大约2硼的距离处（即大约2个原子半径的总和），并且分子分解成碎片的能量大约为0.06 Hartree，这相当于加热到大约20,000开氏度（或摄氏温度，在这里无关紧要）。 为了转换能量，我建议使用诸如this的在线资源。

离子键结合的氢离子的类似情况：



由于μ子氢的玻尔半径较小（请参见上一部分 ），因此在最小势能下，氢核的距离也接近200倍。 该分子的分解能已经超过10 Hartree，相当于温度超过3 lyam度（ $$$\大约（3.2 \ cdot 10 ^ 6）^ \ circ$ ）

为了点火，反应通常需要大约10 ⁸ K的温度，大约是320 Hartree。 让我们看看在普通的divodoron离子的情况下以及在其μ子形式的情况下，在多远的距离处都能获得相似的能量：



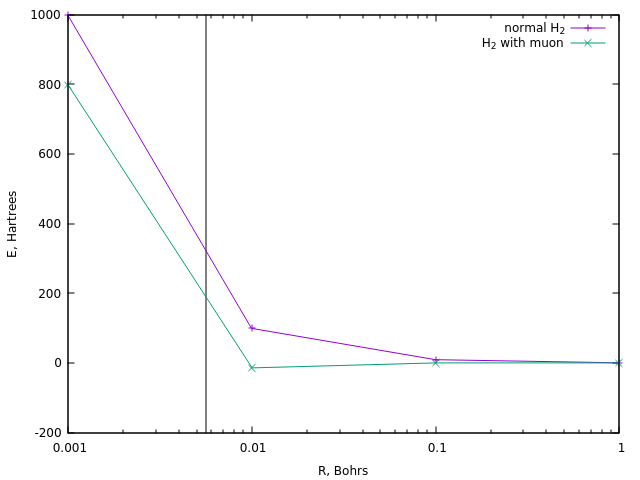
在前者的情况下，这相当于约0.0058硼（垂直线）的距离。

在约190 Ha的能量下，即在μon氢中，实现了类似的距离。 大约少一倍半。 这是对μ子催化温度的最简单估计。

但实际上，一切都会变得更酷。 事实是，如果形成稳定的颗粒 $$$\ mathrm {（{} ^ mH（\ mu ^-）{} ^ nH）^ +}$ ，那么在μ子活着时，这些原子核将相对彼此振荡。 从“两个氢原子”状态到“重核”状态的隧穿可能会发生，隧穿的可能性取决于所需的隧穿长度d $$$p ^ {-d}$ ，因此通过μ子使两个原子核更靠近，我们将大大增加该反应隧穿过程的可能性。 不幸的是，对此效应的估计不再需要量子化学，而需要核物理学，因此，本部分讨论超出了本文的范围。 因此，在此我们将停止。

PS为什么不是那么简单？

实际上，在等离子体条件下形成这些颗粒并不是那么简单。 事实是，如果我们碰撞两个粒子，那么它们的总能量显然超过了离解能（在原子核+电子/介子的情况下为电离能），因此当它们碰撞时，它们不会形成稳定的粒子（原子，离子，分子），而是通过彼此过去。 为了相互坚持，他们需要抛弃一些多余的能量，为此，我们需要额外的第三个人来承担这种能量。 它可以是光子，也可以是某种在附近飞行的剩余粒子，但是最主要的是条件应该有助于这种过量能量的夹带。

PPS

如果您有任何评论/说明/问题，请在评论中或PM中写。 我将纠正所有问题，我将回答并解释所有问题。