在上一篇文章中,我描述了一种算法,该算法可让您在两点之间建立更有趣的路线(而不是像Yandex-Google一样缩短路线)。 该算法从“开放街道地图”中加载了对行人而言既愉悦又有趣的景点,公园和其他物体,并在其中穿越了道路。 结果,路径可能会增加10-20%,但更加有趣。

城市照片-Alex'Florstein'Fedorov
在评论中,许多人写道,除了两点之间的路线外,他们还将对建立在同一点开始和结束并适合给定时间限制的环形路线感兴趣。 例如,如果您有两个小时的火车去或与朋友见面,那么这段时间您将没有时间去很远的地方,但是很可能散步去看看附近的美景。
经过大量实验,我编写了一种遗传算法,在这种情况下,该算法可以构建出非常好的(对我而言)路线。 根据猫的工作原理和一些例子进行说明。
因此,用户希望能够短暂游览周围区域并在指定的时间(通常为1-2小时)内返回起点。 事实证明,这种步行方式非常有需求。 例如,文章“目的地内游客的运动方式”描述了对香港250名游客的足迹的研究,而40%的游客开始从距离酒店500米半径内的圆形路线探索这座城市。 但是,人们常常闲逛,不知道附近有什么有趣的东西。
如果任务不在旅游中心(无论走到哪里,到处都会发现有趣的东西),但是在郊区需要寻找景点的地方,则任务会很复杂。
半径和景点选择
要构建路线,我们首先需要选择我们要参观的景点。 为此,您需要确定起点周围的搜索区域。 如果用户以M分钟为单位定义最大步行时间,则您可以到达并有时间返回的最远点是距离(V * M / 2)的点,其中V是行人的速度。
行人的平均首选速度可以认为是每秒1.4米。 但是,观光时,人会花一些时间在旅行上,因此会慢一些。 我在城市周围建立了一些路线,并沿着它们行走,将步行的时间与应用程序的预测进行了比较。 结果,我的平均步行速度降低了约20%,即 约1.1 m / s。 由于我会定期停下来拍照,因此请查看地图,有时我又过马路以选择最佳角度或购买冰淇淋。

我在城市不熟悉的地区进行了实验,使用我的算法,您可以找到我以前从未听说过的各种有趣的事物。 例如,第一个传单的纪念碑。
选择最大距离处的兴趣点将导致构建退化的环形路径。 由于行人将不再有时间沿着一条直线走最短的路径,因此他将只能参观该景点,然后再沿着同一条街返回,如红色箭头所示。
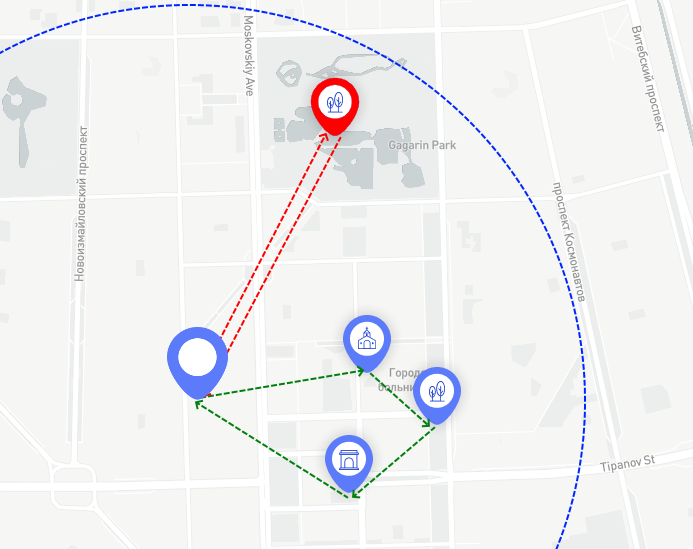
在这里,我们既可以去更远的公园,也可以一次更近地参观几个景点
但是这种情况与有趣的循环路线的想法相矛盾,因为实际上我们只看到了一条街道和一个物体,但是我希望看到最多。 因此,根据实验结果,选择了等于最大距离的三分之一的半径。 使用此搜索半径,行人将有足够的时间沿半径到达最远的兴趣点,然后,如有必要,沿弦走相同的距离以搜索其他有趣的物体,然后及时返回。
正面方法问题
好的,我们汇总了一些候选景点。 现在剩下的是选择我们要检查的对象和顺序。 最有可能的是,我们没有时间去拜访它们,因此我们需要选择它们中最有趣的子集。
首先,我尝试制定和构建一个简单的顺序算法。 但是,我很快遇到了许多问题。
如果考虑上图的情况,则不清楚从何处开始构建路线。 如果公园是最重要但又最遥远的景点,那么从公园开始,我们将得到一个退化的版本,这是我们之前写的。
下一个明显的解决方案是以某种方式将景点聚集在一起,并尝试寻找通往最有利可图的聚集之路,然后走进其中。 但是在这里,一切还不清楚:从哪个集群开始,走什么路。 您总是会陷入我们走错路的陷阱,然后陷入“沙漠”-一个看不到我们没有足够时间返回起点的区域。
从某种意义上说,我很清楚自己实际上正在从事遗传算法的工作:我在地图上绘制了不同的路线,并尝试确定我个人希望它们多少。
遗传算法
收到编号的景点列表后,算法应选择有序子集,这将构成循环路线的基础。 在这种情况下,最终路线是许多关键景点的位置之一 (我们不希望重复,也不需要使用所有可能的物体)。
知道从n到k的放置数量的公式,我们可以估计可能的选项数量。 如果考虑到圣彼得堡宫殿广场周围长达一小时的路线,经过过滤和聚类后半径为1320米(如上所述),将有54个主要景点的候选者。
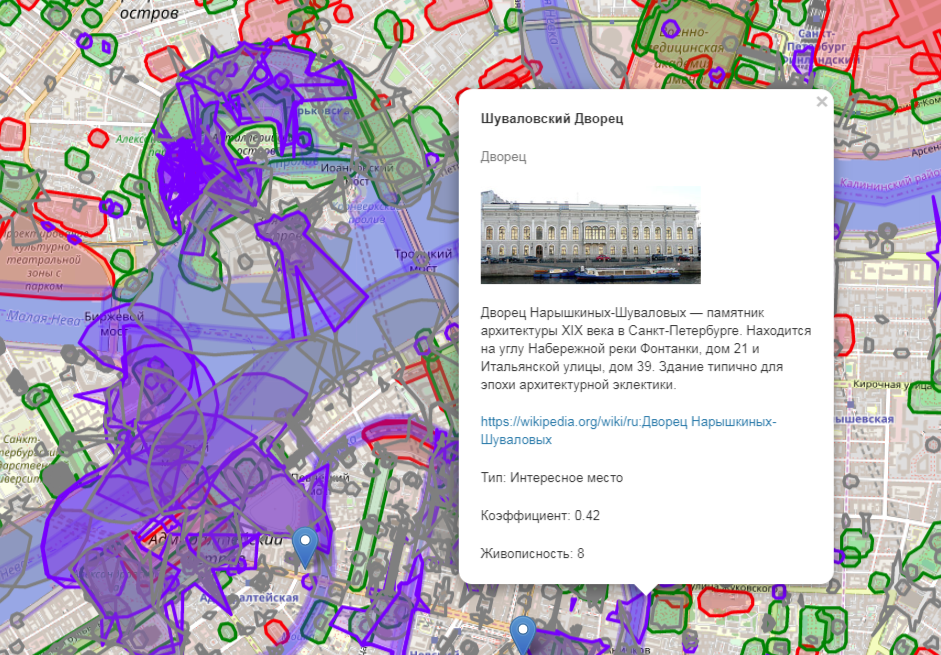
中心一堆景点的地狱粥,根据上一篇文章的算法计算得出的可见区域的调试输出
选择和排序的原理已在上一篇文章中进行了描述,此外,我们还删除了兴趣小于3的对象(出于此类次要对象的考虑,除非附近没有别的东西,否则一个人不太可能准备走得很远)。 因此,可以通过从54到5的展示位置数量的公式计算出可能的路线数量,即379501200。对于2小时的路线(半径范围内已经有151个兴趣点落入),该数字将等于73423236600。那么,对于简单的搜索而言,这太多了。
染色体和遗传算子
在这种情况下,染色体是一条线,其中每个元素都是对应的关键引力的编号。 对于染色体排列或排列的任务,有遗传操作员的特殊优化变体。 这样的操纵子保留了染色体的性质,以保持初始元素组的排列或放置。
- 部分映射交叉(PMX)用于交叉。
- 对于突变,使用两个随机基因(交换突变体)的位置交换。
例如,可以在 “旅行商问题的遗传算法:表示法和运算符的回顾”一文中找到这些运算符的示例操作说明。
健身功能
适应度函数应考虑以下因素以构建有趣的循环路径:
- 所有参观的主要景点的总兴趣应尽可能大。
- 总旅行时间应尽可能接近用户指定的时间,路线不应更长或更短。 只有附近没有足够的景点时,才允许短途旅行。
- 路线不应横穿自己。 对于每个自交点,我们将惩罚百分比添加到函数的总值中。
- 路线的形状应接近圆形,它应占据城市的最大可能区域,并避免情况恶化。 为此,我们在函数中输入由路线描述的图形的面积与搜索景点的圆的面积之比。
这是一个很好的往返行程的例子。 它穿过两个公园,并且从未两次访问同一个地方
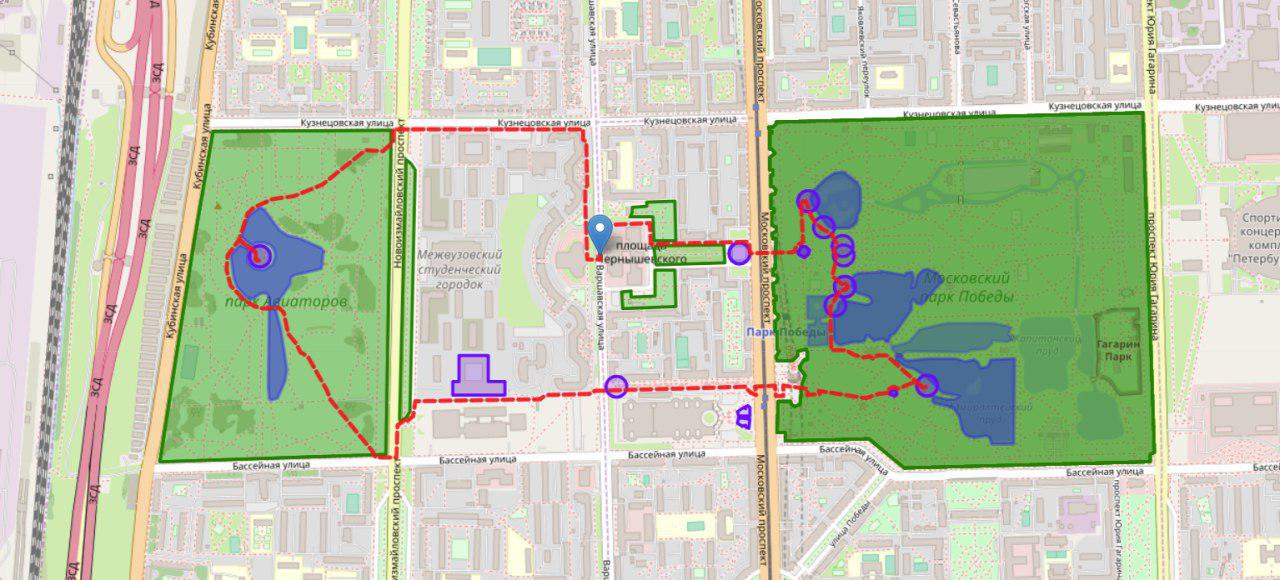
这是一条明显不成功的路线的示例。 它包含死胡同的分支,行人将不得不沿着所检查的路径返回,并具有自动交叉路口。 在十字路口,通常浪费时间来重新检查已经看到的城市部分。
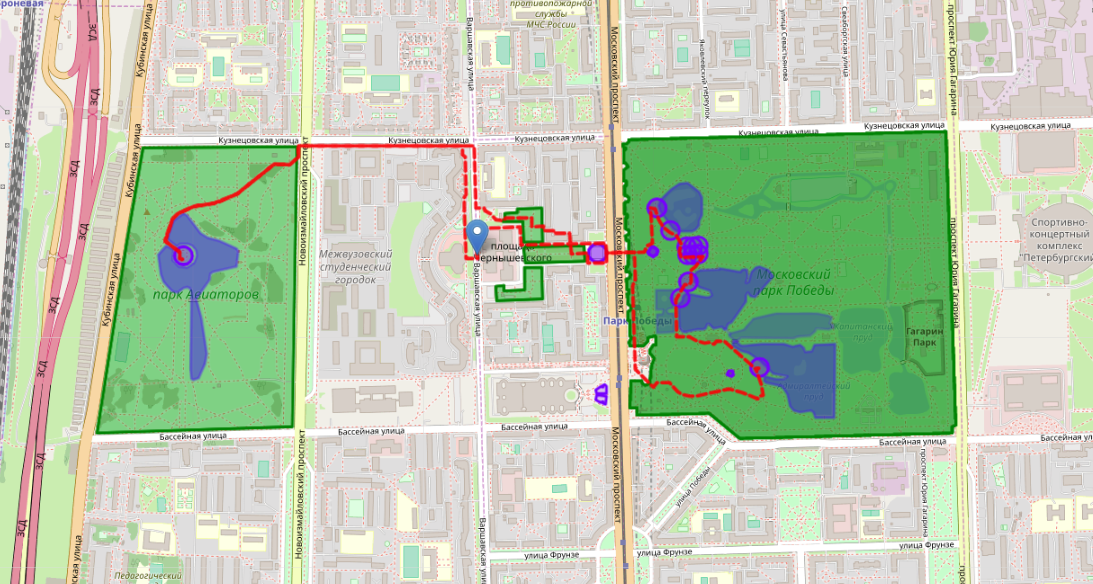
这条错误的路线实际上是通过遗传学获得的,其中第3点和第4点的适应性功能被禁用(自交叉和小范围罚款)
细微差别
在测试过程中,出现了更多细微差别。
超过时间限制
在遗传学工作中,我们计算沿点之间的直线的路径长度。 在使用遗传算法选择了要通信的对象之后,我们正在使用上一篇文章中的算法寻找它们之间的路径。 在这种情况下,路径可能会变长并且无法及时爬网。 毕竟,在城市中,沿着这条街的最短路径通常可能比一条直线长很多倍。
平均而言,差异通常约为10-20%,我们将其放在适应度函数中(即,遗传学会寻找一条具有一定时间裕度的路线,然后在铺设详细路线时将其消耗掉)。 有时这还不够-您必须重新计算路线。 我们在城市中这样的地方 ,路线“像鸟一样”与“像行人一样”相差数公里。
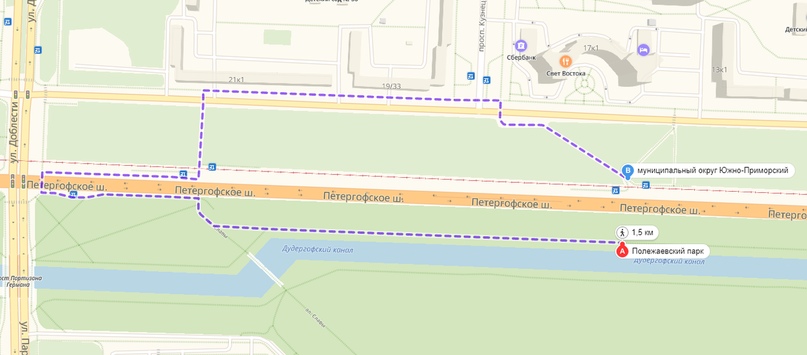
在两点之间直线成50米,但沿着人行道和通道绕行了一个半公里。
但是,尽管如此,该算法有时会超出用户设置的时间,但是每个人都可以自己决定自己是否有10-15分钟的额外时间,或者是否必须提前完成步行。
威尼斯威尼斯
算法准备就绪后,我决定添加欧洲的顶级旅游城市作为娱乐。 事实证明,这很有趣:各地的城市都不尽相同,OSM中的地图绘制功能也是如此,因此,我不得不不断地完成一些工作。
具体来说,在威尼斯寻找圆形路线的搜索失败了。 由于这是一个城市无关区域的独特示例-岛屿之间被大运河隔开,没有桥梁,因此只能通过轮渡才能穿越。

结果,该算法选择了海峡一侧的一部分对象,另一侧的一部分,然后找不到它们之间的陆地路径并掉落。 我必须从起点开始对所有景点的可达性进行检查。
有时您仍然必须以相同的方式回来
在上面有公园的示例中,有一段路线必须以相同的方式返回-这是一个小半岛,上面耸立着带有飞机的纪念碑。 通往半岛的唯一途径是,必须沿着它返回。 因此,不能完全禁止此类退款。 用于此的算法增加了已经走过的所有边缘的权重,减少了沿它们返回的可能性,但仍然使之成为可能。
尽管有时它仍然无法正常工作。 例如,他们抱怨加里宁格勒的主要大教堂。 它位于桥中间穿过的河中的一个小岛上。 从这座桥有一条下降和一条通往大教堂的路径,显然该算法使这条唯一路径的权重增加了太多,这使得返回它无利可图。 结果,尽管这是城市的主要景点之一,他几乎从未进入大教堂。 它仍然需要某种改进。
结果
遗传算法有点不可预测,因此有时会出现故障,并绘制出奇怪的锯齿。 但总的来说,我对结果感到满意。 尤其棒的是,该算法不仅在旅游中心(在这里玩得开心的地方)都有效,而且在城市郊区也都可以使用。 在没有提示的情况下,通常很难找到有趣的东西。
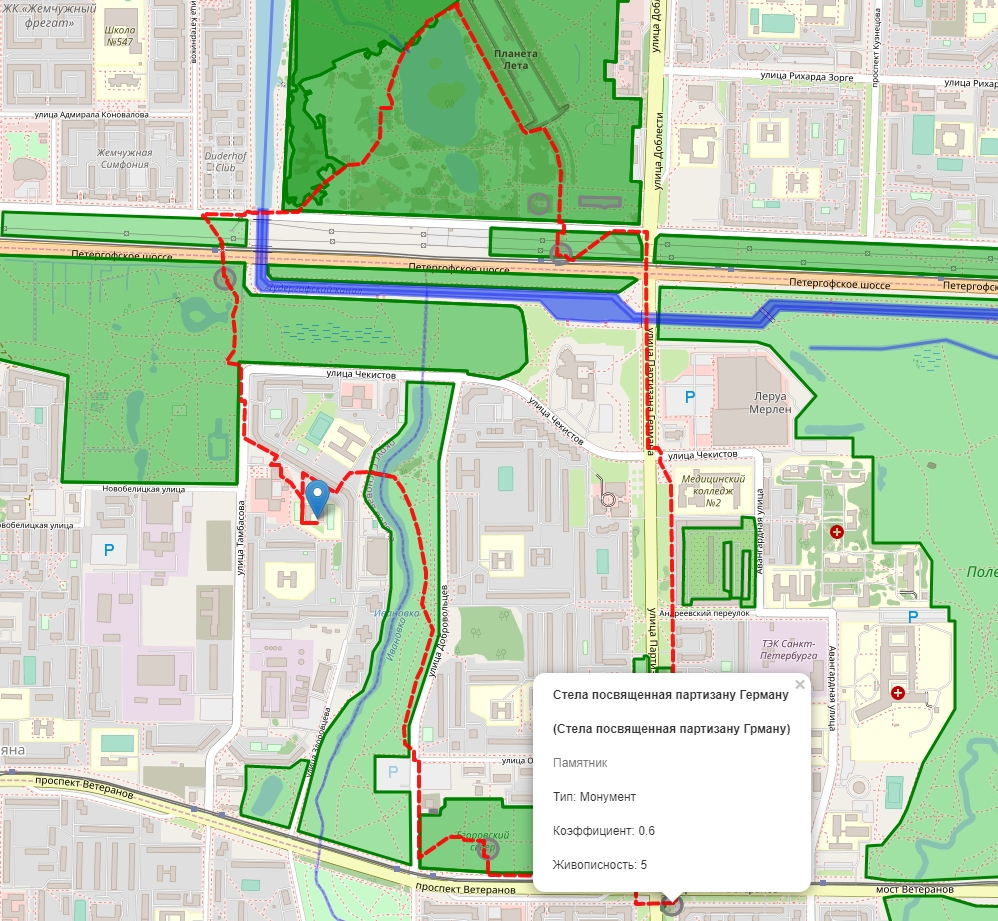
即使在圣彼得堡西南部的睡袋中,您也可以找到足够的古迹,进行两个小时的徒步旅行
您可以在Sight Safari网站或Android应用程序中的77个受支持的城市之一中自行尝试该算法(是的,我们终于完成了它)。
特别有趣的是,该算法如何在地形和海拔高度复杂的城市中工作。 我们在Graphopper探路者库中添加了对高程分析的支持,但我们无法验证它的状态-Peter太平坦了。
通常,尝试撰写评论,是否正确构建了路线。 您可以立即申请添加新城市。