👴 💆 👩🏾‍🌾 无穷类型和脑干 😭 👏🏼 🚖

本文是有关大量数字的文章的延续。但是现在，我们将走得更远-在无穷远中。

为此，我们需要ZFC-集合Zermelo，Frenkel + Choice的理论。选择是选择的公理，是集合论中最具争议的公理。她值得一读。假定您知道集合的“幂”是什么。如果没有，那么谷歌，肯定可以说比我更好。在这里我只会提醒一些

已知事实

一组整数的幂表示为 $\ aleph_0$ 。这是第一个无限次幂；此类集合称为可数。
整数的任何无限子集的幂都是简单的，偶数等。 -也可数。
有理数集（即分数p / q）也是可数的；它们可以被蛇传递。
对于任何电源，都有一个电源设置操作-所有子集的集合产生的功率要大于原始功率集。有时，此操作称为将二提高为幂，即 $powerset（\ aleph_0）= 2 ^ {\ aleph_0} = \ aleph_c$ 。计算出的幂的幂集就是连续体的幂。
连续性能力由以下组成部分：有限和无限的部分，平面和体积的图形，甚至整个n维空间
对于普通数学，以下幂 $powerset（\ aleph_c）$ 几乎不需要，通常所有工作都是通过可数集和连续幂集进行的

现在

鲜为人知的事实

在ZFC中，并非所有元素集合都可以设置。收集的范围如此之广，以至于无法设置它们；这会产生悖论。特别地，“ 所有集合的集合 ”不是集合。但是，存在允许这种集合的集合理论。

再远一点集合论...什么对象？数字？一个苹果？橘子？奇怪的是，ZFC不需要任何对象。取空集{}，并同意它的意思是0。1用{{}}表示，{{{}}}}来表示，依此类推。 {5,2}是{{{{{{{}}}}}}，{{{}}}}。使用整数，我们可以创建实数，并且实数的集合可以创建任何形状。

因此，集合论是……怎么说……空心理论。这个理论什么都没有。更准确地说，是关于如何嵌套（嵌套，即相互放入）花括号。

集合论中定义的唯一运算是

$\在$ -归属感的象征。但是统一，排斥，平等等等呢？这些都是宏，例如：

$（A = B）\等值\ forall x（（A中的x \）=（B中的x \））$

也就是说，在翻译成俄语时，当测试任何属于它们的元素时，两个集合被认为是相同的

这些集合不是有序的，但是可以固定的：让有序对（p，v）为{{p}，{p，v}}。从程序员的角度来看，这并不算什么，但是对于一个数学家来说已经足够了。现在，所有参数值对的集合都设置了一个函数，该函数现在也已设置！瞧！所有在二阶语言水平上进行的数学分析，因为它不是在讲数字的存在 ， 而是在讲函数的存在 ，因此崩溃为一阶语言！

因此，集合论是一个糟糕的理论，没有对象，只有一个关系图标，它具有绝对强大的力量-没有任何新的假设，它就从形式算术，实数，分析，几何等等产生。这是一种TOE数学。

连续假设-CH

之间是否有力量

$\ aleph_0$ 和

$2 ^ {\ aleph_0}$ ？康托尔不能解决这个问题；“数学家之王”希尔伯特赞扬了它的重要性，但直到后来才证明，这一假设既不能被证明也不能被证明。她独立于ZFC。

这意味着您可以创建两个不同的数学运算：一个是ZFC + CH，另一个是ZFC +（不是CH）。实际上，甚至超过两个。假设我们拒绝CH，也就是说，我们相信

$\ aleph_0$ 和

$2 ^ {\ aleph_0}$ 仍然有力量。可以有几个？一二戈德尔相信只有一个。但是，事实证明，假设其中有2个，17个，19393493个并不会导致矛盾。任何数量，但不是无限！

当在形式算术中遇到不可证明的陈述时，出于某些原因，我们知道尽管该陈述无法证明，但实际上是对还是错。在集合论中这是行不通的，我们实际上得到了不同的数学家。如何与此相关？有三种哲学方法：

形式主义：为什么实际上会感到惊讶？我们设置符号游戏的规则，不同的规则-不同的结果。无需寻找不存在的问题

柏拉图主义：但是，然后如何解释基于完全不同的原理的完全不同的理论（例如ZFC和新基金会）几乎总是得出相同的结果？这是否意味着公式背后是我们正在研究的某种现实？例如，戈德尔（Godel）持这种观点

多元宇宙：我们可以有许多公理学，有时给出相同的结果，有时却没有。我们必须从整体上理解图片-如果颜色与不同的公理系统相关联，那么彩色的效果树就是数学。如果到处都是真实的东西-它是白色的，但也有彩色的分支。

越来越高。

在未来，为简单起见，我们将接受连续假设，即

$powerset（\ aleph_0）= \ aleph_1 = \ aleph_c$ -非常方便。实际上，我们也将接受更强的公理，即在x和幂集（x）之间永远不存在中间幂的广义连续假设。现在我们迭代powerset，一切都很简单：

$\ aleph_0 \ rightarrow \ aleph_1 \ rightarrow \ aleph_2 \ rightarrow ... \ rightarrow \ aleph_ {36463634} \ rightarrow$

我们能走多远？经过无数次迭代后，我们得出

$\ aleph_ \ omega$ -无限的力量！顺便说一下，它的存在对康托尔并不明显。但是一秒钟！毕竟，powerset功能始终是定义的，因此

$\ aleph_ \ omega$ 不能成为最后一个！

$\ aleph_ \ omega \ rightarrow \ aleph _ {\ omega + 1} \ rightarrow \ aleph _ {\ omega + 2} \ rightarrow ...$

得到

$\ aleph _ {\ omega + 3}$ 有必要重复powerset无限次以上三遍 。您已经开始拆除屋顶了吗？否则会的。又一次，因为迭代无穷大的次数，我们得到了

$\ aleph _ {\ omega + \ omega} = \ aleph _ {\ omega2}$ ，然后自然

$\ aleph _ {\ omega2 + 1}$

无限次达到无穷大之后 ，我们获得了索引

$\ omega ^ 2$ 。您如何看待这种力量，例如：

$\ aleph _ {\ omega ^ 3 + \ omega ^ 2 + \ omega4 + 48745}$ ？当我们遍历序数列表上的幂集时，以下是初始序数：

但是还有很多很多因此，我们将立即跳过并执行

立即迈出一大步

注意！以下内容可能对您的大脑有害！我们迭代了powerset数次，但是我们不是挥舞连续体吗？老实说，我本人有点不满意，因为循环可以连续执行多次，但是集合论需要存在

$\ aleph _ {\ aleph_1}$

接下来，我们会更快：

$\ aleph _ {\ aleph_1} \ rightarrow \ aleph _ {\ aleph_2} ... \ rightarrow \ aleph _ {\ aleph_ \ omega} = \ aleph _ {\ aleph_ \ aleph} \ rightarrow$

最后一个Alef的索引为零，但是本地乳胶不允许将其放置-级别太多。但是最主要的是，您了解了，无论我们将创造多大的新奇力量，是的，这只是一个中继器 ，并将整个结构以索引的形式放入新的Aleph中。现在容量像雪球一样增长，我们不能停止，Alephs的金字塔更高，我们可以创造任何力量……还是不？

功率不可达

如果有这么大的力量怎么办

$\ theta$ 无论我们如何尝试从Alephs建筑物“从下方”到达建筑物，我们都无法实现？事实证明，这种能力的存在与ZFC无关。您可以接受它的存在与否。

我听到了奥卡姆剃刀的低语……不，不。数学家遵循相反的原则，即本体论的极大主义 -让一切可能存在。但是我至少要接受两个以上的理由。

首先，这不是我们知道的第一个无法实现的力量。首先...这是熟悉的计数能力。奇怪的是，它具有无法获得的所有属性-通常不这样称呼它：
无法“从下面”获得无限次幂-既不添加元素有限次，也没有迭代powerset（）有限次，使用有限集进行播种，您将不会获得无限次。要获得无限，您必须已经将其放置在某处。
无限功率的存在是由特殊公理-无限公理引入的。没有它，就无法证明无限力量的存在。

第二：如果我们拒绝无穷大公理，我们会得到FinSet，这是一个带有有限集的简单玩具集理论。让我们写出所有这些集合（所谓的理论模型 ）

{}
{{}}
{{{}}，{}}
{{{{}}}}
{{{{}}}，{{}}}
{{{{}}}，{{}}}
{{{{}}}，{{}}，{}}
...

然后，我们得到...无限集的无限集...也就是说，有限集理论的模型是无限的，并在其中扮演“所有集合的集合”的角色。也许这将有助于理解为什么理论不能谈论“所有集合的集合”-这样的集合总是作为模型存在于理论之外，并且具有除集合内部以外的其他属性。您不能将无限添加到有限集的理论中。

是的

$\ theta$ 这是ZFC理论的“众生”。在此视频中，最后非常漂亮地谈到了无法实现的功能，但我们必须继续。

更进一步。

当然，我们可以通过迭代来走得更远

$powerset（\ theta）$ 。经过上述所有步骤之后，建造了大型中继塔，我们再次遇到了无法企及的主教（但现在我们不需要新的公理，因为我们刚刚添加了存在无法企及的权力的公理，这已成为可证明的）。一遍又一遍。

$\ theta_0 \ rightarrow \ theta_1 \ rightarrow \ theta_2 \ rightarrow ... \ rightarrow \ theta_ {36463634} \ rightarrow$

请注意，现在的箭头对我们来说不像执行Powerset（）函数，而是GetNextInaccessible（）。否则，一切看起来都非常相似，我们有：

$\ theta _ {\ theta_1} \ rightarrow \ theta _ {\ theta_2} ... \ rightarrow \ theta _ {\ theta_ \ omega} \ rightarrow \ theta _ {\ theta_ \ theta} \ rightarrow$

现在，我们一定会实现任何目标……还是没有？

大容量层次结构。

是的，有了GetNextInaccessible，我们遇到了不可思议的力量。它的存在需要另外一个公理。有超级无法达到的能力。依此类推。但是，还有其他方法来确定权力，不仅是通过不可企及性：

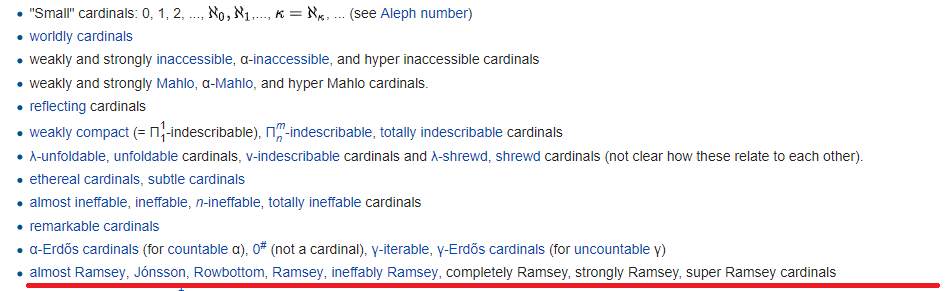
通常，每个链接的后面是一个完整的无休止的层次结构，其中包含任意数量的超级和中继器前缀。但是，确定无法达到的基数的公式总数并不大-因为公式的数目是可数的！因此，它们迟早会结束。它们结束的地方画了一条红线。此行下的所有内容（尽管是正式的）都更加不稳定。

红线本身标志着哥德尔宇宙的终结（但不要忘记，哥德尔创造了两个不同的宇宙）-从下面使用公式构造的集合的宇宙。红线上方的容量称为hmm，“小”，而下方-大的容量：

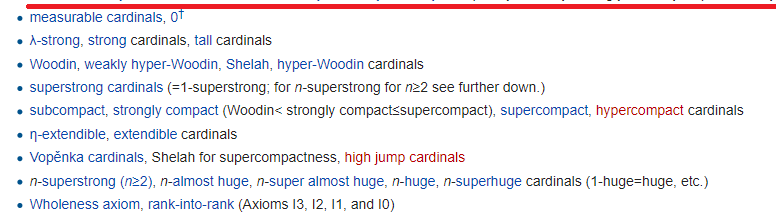
它们的主要思想是，集合的范围变得如此之大，以至于它开始以不同的意义重复出现。像往常一样，每行都需要一个单独的公理，并且需要多个公理。更有趣的是，所有这些都不如您想像的那样无用。例如，需要最底端的最强公理来证明有关药片的事实。

下面是一个调查，最后选择在这里解密。

无穷类型和脑干