很难重新考虑任务的概念,但是结果值得。
 作者的注释
作者的注释 :我知道我在经典和量子情况下都错误地计算了布拉格转移。 但是,它足够接近事实,以了解对经典计算机和量子计算机进行编程的区别。
时间:2018年的某个时间。 位置:斯拉卡烂通道。
“你知道Python吗?”
Ars Technica的科学主管John Timmer的问题有时可能会令人惊讶。 如果可以谨慎地在Slaka中浸渍字母,那么我的回答“是”将只是渗入其中。
事实证明,D-Wave决定通过API向全世界提供其量子优化器的访问权限。 Ars邀请他尝试,但是您需要了解Python。 我已经准备好了。
我以为D-Wave会发布某种奇妙的API,该API可能会使我的专有代码使程序员大哭,并将其变成量子优化的产品。 las,当我使用量子优化器时,事实并非如此。 我很快发现自己沉迷于文档中,试图弄清我需要做什么。
我认为D-Wave公共关系代表想到的是一个足够了解可以运行现成示例的人。 但是我很固执。 我需要提出三个或四个可能要测试的任务。 我想找出:我可以掌握在D-Wave计算机上解决这些问题的过程吗? 从经典编程到使用量子退火的概念上的跨越,有多么容易? 我的至少某些任务是否适合这台机器?
我马上说出一个惊人的结论,答案如下:也许不是完全“掌握”; 困难 并非所有任务。
选择编程任务
尽管您以我的方式想象,但我可以被称为实践程序员。 本质上,任何对编程有很好理解的人在看到我的Python代码后都会做鬼脸(甚至可能犯下谋杀罪)。
但是,我可以提出需要编写程序来解决它们的任务。 例如,我需要一些可以计算一组电极的电场的东西。 一种能找到具有最小氦原子能的状态的东西。 还是可以算出激光启动时光强度增加的东西。 这些任务使我最感兴趣。 在开始这个项目时,我不知道D-Wave架构是否可以解决这些问题。
我认为有两个可行的问题:找到Mandelbrot组的成员并计算一组电极的电位轮廓。 这些问题的优点是,我可以使用经典代码快速解决它们并比较答案。 但是我很快遇到了问题,试图弄清楚如何在D-Wave的机器上开始解决这些问题。 这要求在理解任务方面有重大转变,而且我的思维非常简单。
例如,我遇到的问题之一是我们正在处理低级二进制数(尽管它们以qubit而不是bit的形式表示)。 这实际上意味着该程序没有类型。 我几乎所有的编程经验都是使用浮点数字类型解决物理问题。
您必须对任务有不同的思考:答案应表示为二进制数(理想情况下为真或假),而所有物理学(例如,所有浮点数)均应通过组合量子位来表示。 即使我的生活取决于它,我也无法弄清楚如何完成我的任何任务。 沉浸在教学中,我让这个问题在我自己的果汁中沸腾了一下。
六个月后,我终于遇到了一个我熟悉的问题,该问题可以用D-Wave计算机解决。 光通过光纤布拉格光栅的过程可以表示为一个二元问题:光子是否从滤光片中出来? 所有物理学都包含在量子位化合物中,并且答案是从解的能量中提取的。
布拉格光栅
一维布拉格光栅是多层材料。 两层之间的每个间隙反射少量的光。 通过整个结构的总穿透力由间隙之间的距离决定。 为了使光通过,必须将不同间隔的波同相相加。 具有50层,反射率为0.1%的理想布拉格光栅的通过光谱如下所示。
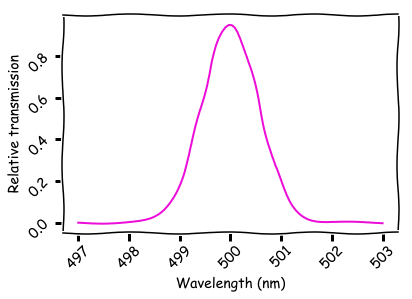
以下代码为该图生成数据:
ld = np.linspace(ld_center-3e-9, ld_center+3e-9, num_ld) k = 2*np.pi/ld T = np.ones(ld.shape) for j in range(num_layers): T = T*(1-A)*np.cos(j*k*layer_sep)**2
在这里,我们显式计算到达下一个间隙的每个间隙的相对贡献,以光功率表示。 通过减少或增加间隙的影响来考虑相长干涉和相消干涉,这取决于层之间的距离与波长的一半重合的接近程度。
这种破解是必要的,因为量子位的连接仅用实数表示,而不用复数表示(物理最好通过包含光的振幅和相位的复数表示)。 不过,经典代码的输出看起来大约是正确的-缺少边带会有点令人担忧,这表明该模型不完整,但到目前为止并不重要。
经典模型代码缺少一致性检查。 我计算了结果,并准确建议了波将如何传播。 即使这个假设是错误的,计算结果也将是相同的-尽管所有方程都是基于物理学的,但是不可能在代码中保证它们正确地描述了它。
我们传递给量子
在D-Wave系统中,有必要创建一个量子比特链,每个量子比特表示间隙中的光强度。 每个量子位与其邻居相关联,并且连接的权重代表了从一个间隙到另一个间隙的通道,并考虑了接口之间的距离。 如果界面之间的距离等于波长的一半,则光会在两个界面之间发生共振并继续传播。 如果距离是波长的四分之一,则会触发相消干扰,并且连接应最小。
穿过一个间隙表示为99.9%,因此零和第一个量子位之间的连接为
在第一和第二之间:
在第二和第三之间:
在该公式中,d是层之间的物理距离,并且λ是波长。 如果d /λ= 0.5,则余弦等于1,我们可以期望光的理想透射。
在D-Wave系统中,这意味着必须按以下方式连接每两个相邻的qubit:
在此表达式中,度u考虑了先前的量子位的影响并简化了连接方案。
任务执行
现在,知道了如何连接量子位后,我们必须查看量子位的物理连接来决定如何完成此任务。 这称为次要嵌入。
我们必须给计算机列出量子位之间的连接及其权重。 我们还必须指定表明每个量子位重要性的偏差。 在我们的例子中,所有量子位都同等重要,因此对于所有量子位,它们都设置为-1(我从标准示例中获取了此数字)。 偏差和连接必须与物理量子位及其之间的关系相关联。 对于大型任务,搜索此类映射可能会花费很长时间。
生成关系和偏差的代码非常简单。
幸运的是,D-Wave API会尝试自行找到一个小的实现。 我发现它适用于50层的过滤器,但不能处理100层。 这对我来说似乎很奇怪,因为它具有2,000个量子位,并且链长为1(我们不需要合并多个物理量子位来创建一个逻辑位),所以系统必须能够实现更大的问题。 回顾过去,我相信失败是由于我要求太多零连接的缘故。
另一种方法是不明确定义空键。 这使算法可以自由地在qubit没有连接的情况下找到更多的实现选项。 我没有尝试过,但是在我看来,此选项是下一步的选择。
无论如何,启动D-Wave机器非常简单:
response = EmbeddingComposite(DWaveSampler()).sample_qubo(Q_auto, num_reads=num_runs)
学方言
我的经典算法与D-Wave解决方案之间的区别在于D-Wave计算机不会直接返回清晰的结果。 事实证明它分为许多部分。 我们得到了一个能量列表,其中最小的应该是解决方案。 对于每种能量进行几次运行(例如1000次),我们得到它出现在答案中的次数。 对于每次运行,我们都会得到一个“响应”,即量子比特的值。 我现在还不清楚这些值中的哪些可以(并且可以)解释为通过过滤器。
最后,我决定最小的解决方案能量将是最佳答案,因为该值在某种意义上代表了存储在滤波器中的能量。 因此,具有较高能量的解决方案表示过滤器的渗透率更高,如下所示。 对于那些了解这一点的人来说,将这个答案变成一条真实的光明之路是功课。

通过检查具有最低能量的解决方案中的量子位值,也可以获得过程的物理表示。 在下面,您可以看到溶液的位值,分别对应于透射曲线的峰值(500 nm),50%的透射率(500.6 nm)和5%的透射率(501.4 nm)。
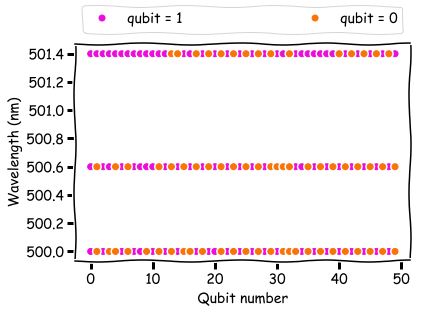
在传输峰值的边缘,量子位倾向于以单元组的形式累积。 在峰值处,量子位在0和1之间交替。最后一个解决方案是关于布拉格光栅中的光强度如何变化的二进制图片。 换句话说,D-Wave解决方案还直接表示物理,这对于我的经典代码无法说。
这是量子退火的真正强度。 是的,我可以从经典计算中完美得出通过滤波器的曲线。 但是要了解内部实际发生的情况,您需要更复杂的代码。 在量子退火中,这是完全免费的。 我认为这很酷。
量子退火的另一个优点是,它可以保证在我选择的量子位键重范围内提供一致的解决方案。 这意味着量子计算机的解决方案可能比从经典代码获得的解决方案更可靠。
关于量子编程的讨论
对D-Wave机器进行编程最困难的部分是您需要对任务进行不同的思考。 例如,当曲线与数据重合时,我习惯于将问题最小化。 但是我发现很难改变您对物理问题的思考方式,以便您开始编写代码来解决它。 该公司提供的大多数示例对我来说似乎都是抽象的且不适合物理问题,这无济于事。 但是,当越来越多的用户开始发布他们的代码时,这种情况将会改变。
同样,答案的解释可能会出现困难。 基本上,我喜欢API的简单性,并且免费获得其他想法很棒。 在不久的将来,我可以使用D-Wave解决实际问题。