Geekly articles weekly

异国数据结构：修改后的Merkle Patricia Trie

“我应该牢记所有这些该死的算法和数据结构是什么样的魔鬼？”


关于这一点，可以归结为大多数有关技术采访通过的文章的评论。 通常，主要的论点是，以一种或另一种方式使用的所有东西都已经被实施了十次，并且这位普通程序员不太可能必须处理。 好吧，在某种程度上这是事实。 但是，事实证明，并不是所有的事情都得到了实现，不幸的是（或者幸运的是，我）仍然必须创建一个数据结构。


神秘修饰的默克尔·帕特里夏·特里。


由于在哈勃尔树上以及在媒介上根本没有关于这棵树的信息-还有一点，我想告诉你它是哪种动物，以及它是怎么吃的。


KDPV


这是什么


免责声明：对我来说，实施的主要信息来源是黄皮书 ，以及源代码parity-ethereum和go-ethereum 。 关于某些决定的合理性的理论信息很少，因此，做出某些决定的原因的所有结论都是我个人的。 万一我在某件事上弄错了，我会很高兴在评论中更正。


树是作为连接的非循环图的数据结构。 这里的一切都很简单，每个人都对此很熟悉。


前缀树是根树，可以在其中存储键-值对，这是因为节点分为两种类型：包含路径一部分（前缀）的节点和包含存储值的叶节点。 当且仅当使用键，我们可以从树的根部一直走到最后找到一个具有值的节点时，树中才会存在一个值。


PATRICIA树是一个前缀树，其中的前缀是二进制的-也就是说，每个关键节点都存储有关一位的信息。


Merkle树是基于某种数据链构建的哈希树，将这些相同的哈希表聚合为一个（根），存储有关所有数据块状态的信息。 也就是说，根哈希是一种区块链状态的“数字签名”。 这个东西在区块链中被积极使用，更多信息可以在这里找到。


努力是...


总计：修改过的Merkle Patricia Trie（以下简称MPT）是一种散列树，用于存储键值对，并且键以二进制形式表示。 到底是“修改”的内容，我们在稍后讨论实现时会发现一点。


怎么会这样


在以太坊项目中使用MPT来存储有关帐户，交易，其执行结果以及系统功能所需的其他数据的数据。
不像比特币那样，状态是隐式的，并且是由每个节点独立计算的，每个账户的余额（以及与之关联的数据）直接存储在空中的区块链上。 此外，必须以密码方式提供数据的位置和不变性-很少有人会使用其中无需客观原因即可更改随机账户余额的加密货币。


以太坊开发人员面临的主要问题是创建一个数据结构，该结构可以有效地存储键值对，同时提供对所存储数据的验证。 于是MPT出现了。


怎么了


MPT是前缀PATRICIA树，其中的键是字节序列。


这棵树的边缘是半字节序列（半字节）。 因此，一个节点最多可具有十六个后代（对应于从0x0到0xF的分支）。


节点分为3种类型：


  • 分支节点。 用于分支的节点。 最多包含1到16个到子节点的链接。 也可能包含一个值。
  • 扩展节点。 一个辅助节点，存储一些子节点共有的路径的某些部分，以及位于下面的分支节点的链接。
  • 叶节点。 包含路径的一部分和存储值的节点。 这是链中的终点。

如前所述，MPT建立在另一个kv存储库的顶部，该存储库以“链接” =>“ RLP编码节点”的形式存储节点。


在这里，我们提出了一个新概念：RLP。 简而言之，这是一种对表示列表或字节序列的数据进行编码的方法。 示例： [ "cat", "dog" ] = [ 0xc8, 0x83, 'c', 'a', 't', 0x83, 'd', 'o', 'g' ] 。 我不会特别详细，在实现中，我将使用现成的库，因为对该主题的覆盖也会使本来已经很大的文章充实。 如果您仍然感兴趣，可以在此处阅读更多内容。 我们将自己限制在可以在RLP编码数据并将其解码回来的事实。


到节点的链接定义如下：如果RLP编码节点的长度为32个字节或更多字节，则该链接是该节点的RLP表示形式的keccak哈希。 如果长度小于32个字节，则链接是节点本身的RLP表示形式。


显然，在第二种情况下，无需将节点保存到数据库，因为 它将完全保存在父节点中。


官员不同


三种类型的节点的组合使您可以在键很少的情况下有效地存储数据（然后大多数路径将存储在扩展节点和叶节点中，并且分支节点将很少），并且在节点很多的情况下（路径将不会显式存储）但它们会在通过分支节点的过程中“聚集”。


使用各种节点的树的完整示例：


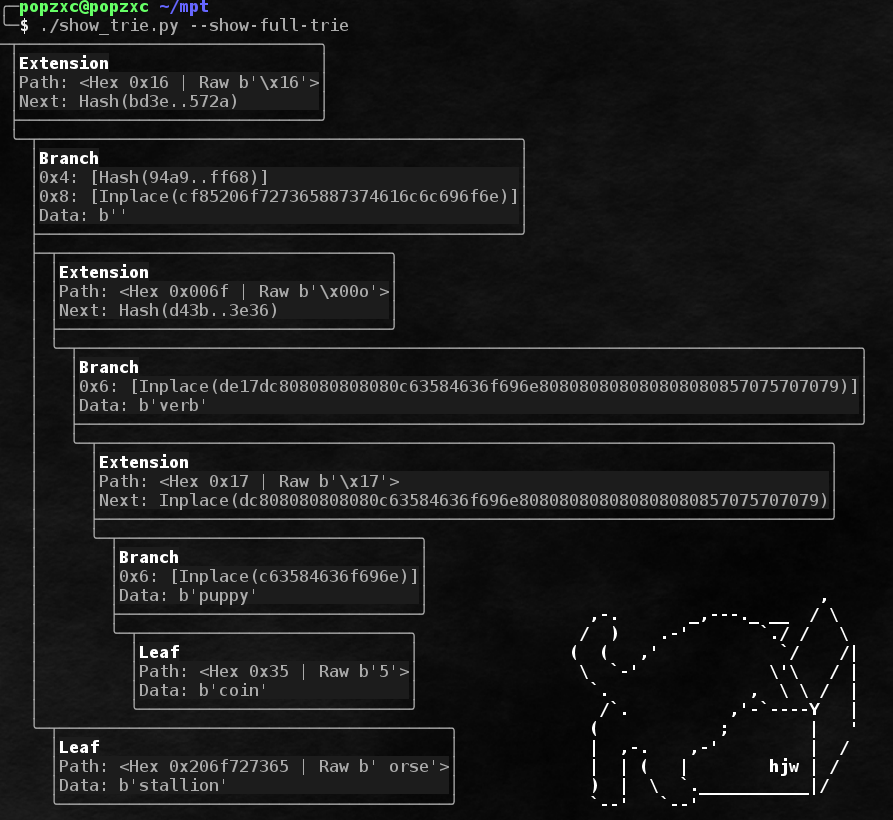
树已满但不厚


您可能已经注意到，路径的存储部分带有前缀。 出于多种目的需要前缀：


  1. 区分扩展节点和叶节点。
  2. 对齐奇数个半字节的序列。

创建前缀的规则非常简单：


  • 前缀占用1个半字节。 如果路径长度（不包括前缀）为奇数，则路径在前缀之后立即开始。 如果路径长度是偶数，要在前缀后对齐，请先添加半字节0x0。
  • 前缀初始为0x0。
  • 如果路径长度为奇数，则将0x1添加到前缀（即使为-0x0）。
  • 如果路径通向叶节点，则将0x2添加到前缀，如果将0x0添加到Extension节点。

我认为在Beatiks上会更清楚：


 0b0000 =>  , Extension  0b0001 =>  , Extension  0b0010 =>  , Leaf  0b0011 =>  , Leaf

去除不是去除


尽管树具有删除节点的功能，但实际上，一旦添加的所有内容将永远保留在树中。


为了不为每个块创建完整的树，而是仅存储树的新旧版本之间的差异，这是必需的。


因此，使用不同的根哈希作为入口点，我们可以获得树曾经处于的任何状态。


用笔写的是什么...


这些并不是全部优化。 还有更多，但我们不再赘述-因此文章很大。 但是，您可以自己阅读 。


实作


理论已经结束，让我们继续实践。 我们将使用来自IT领域的lingua franca，即python 。


由于将有很多代码，并且对于本文的格式，将不得不减少和划分很多工作，我将立即留下指向github的链接。
如有必要，您可以在那里看到整个图片。


首先，我们定义要作为结果的树接口：


 class MerklePatriciaTrie: def __init__(self, storage, root=None): pass def root(self): pass def get(self, encoded_key): pass def update(self, encoded_key, encoded_value): pass def delete(self, encoded_key): pass

界面非常简单。 可用的操作包括获取，删除，插入和更改（与更新结合），以及获取根哈希。


存储将被转移到__init__方法-一种类似dict的数据结构，我们将在其中存储节点以及root -树的“顶部”。 如果None作为root传递，我们假定树为空，并且从头开始工作。


_Remark：您可能想知道为什么方法中的变量被命名为encoded_key和encoded_value ，而不仅仅是key / value 。 答案很简单：根据规范，所有键和值都必须以RLP编码。 我们不会为此烦恼，而将这一职业留给图书馆用户。


但是，在我们开始实现树本身之前，必须完成两个重要的工作：


  1. 实现NibblePath类，该类是NibblePath半字节，以免对其进行手动编码。
  2. 在此类的框架内实现Node类Extension ， Leaf和Branch 。

半路


因此， NibblePath 。 由于我们将在树上四处移动，因此我们班级功能的基础应该是能够从路径的开头设置“偏移”，以及接收特定的半字节。 知道了这一点，我们定义了类的基础（以及下面用于处理前缀的几个有用的常量）：


 class NibblePath: ODD_FLAG = 0x10 LEAF_FLAG = 0x20 def __init__(self, data, offset=0): self._data = data # ,   . self._offset = offset #      def consume(self, amount): # "" N      . self._offset += amount return self def at(self, idx): #      idx = idx + self._offset #    ,   ,    , #   ,    -      . byte_idx = idx // 2 nibble_idx = idx % 2 #   . byte = self._data[byte_idx] #      . nibble = byte >> 4 if nibble_idx == 0 else byte & 0x0F return nibble

很简单，不是吗？


仍然仅编写用于对半字节序列进行编码和解码的功能。


 class NibblePath: # ... def decode_with_type(data): #   : # ,     ,    . is_odd_len = data[0] & NibblePath.ODD_FLAG == NibblePath.ODD_FLAG is_leaf = data[0] & NibblePath.LEAF_FLAG == NibblePath.LEAF_FLAG #    ,     #    . offset  , #       "" . offset = 1 if is_odd_len else 2 return NibblePath(data, offset), is_leaf def encode(self, is_leaf): output = [] #    ,       . nibbles_len = len(self._data) * 2 - self._offset is_odd = nibbles_len % 2 == 1 #  . prefix = 0x00 #    ,    . #      (self.at(0))     . #           (0x0). prefix += self.ODD_FLAG + self.at(0) if is_odd else 0x00 #  ,  Leaf node,  . prefix += self.LEAF_FLAG if is_leaf else 0x00 output.append(prefix) # ,      ,  . pos = nibbles_len % 2 #          , #     2 ,    , #     , #    . while pos < nibbles_len: byte = self.at(pos) * 16 + self.at(pos + 1) output.append(byte) pos += 2 return bytes(output)

原则上，这是方便进行轻咬的最低要求。 当然，在当前的实现中，仍然存在许多辅助方法（例如combine ，将两条路径合并为一个），但是它们的实现非常简单。 如果有兴趣，可以在此处找到完整版本。


结点


众所周知，我们的节点分为三种类型：叶子，扩展和分支。 所有这些都可以进行编码和解码，唯一的区别是存储在内部的数据。 老实说，这就是要求的代数数据类型，例如，在Rust ，我本着一种精神写了一些东西：


 pub enum Node<'a> { Leaf(NibblesSlice<'a>, &'a [u8]), Extension(NibblesSlice<'a>, NodeReference), Branch([Option<NodeReference>; 16], Option<&'a [u8]>), }

但是，python中没有这样的ADT，因此我们将定义Node类，并且在其中有三个与节点类型相对应的类。 我们直接在节点类中实现编码，并在Node类中实现解码。


但是，实现是基本的：


叶：


 class Leaf: def __init__(self, path, data): self.path = path self.data = data def encode(self): #    --    , #   -  ,   -  . return rlp.encode([self.path.encode(True), self.data])

扩展名：


 class Extension: def __init__(self, path, next_ref): self.path = path self.next_ref = next_ref def encode(self): #    --    , #   -  ,   -    . next_ref = _prepare_reference_for_encoding(self.next_ref) return rlp.encode([self.path.encode(False), next_ref])

分行：


 class Branch: def __init__(self, branches, data=None): self.branches = branches self.data = data def encode(self): #    --    ,  #  16 -     (  ), #   -   (  ). branches = list(map(_prepare_reference_for_encoding, self.branches)) return rlp.encode(branches + [self.data])

一切都非常简单。 唯一可能引起问题的是_prepare_reference_for_encoding函数。


然后我承认，我不得不使用一个小拐杖。 事实是，所rlp的rlp库以递归方式解码数据，并且众所周知，到另一个节点的链接可以是rlp数据（如果编码节点的长度少于32个字符）。 使用两种格式的链接（哈希字节和解码的节点）非常不方便。 因此，我编写了两个函数，这些函数在解码节点之后以字节格式返回链接，并在保存之前根据需要对其进行解码。 这些功能是：


 def _prepare_reference_for_encoding(ref): #    ( ,   ) --  . #       :) if 0 < len(ref) < 32: return rlp.decode(ref) return ref def _prepare_reference_for_usage(ref): #     -   . #          . if isinstance(ref, list): return rlp.encode(ref) return ref

通过编写Node类来完成节点。 其中只有2种方法：解码节点并将该节点转换为链接。


 class Node: # class Leaf(...) # class Extension(...) # class Branch(...) def decode(encoded_data): data = rlp.decode(encoded_data) # 17  -  Branch . if len(data) == 17: branches = list(map(_prepare_reference_for_usage, data[:16])) node_data = data[16] return Node.Branch(branches, node_data) #    17,   2.   - . #      ,     . path, is_leaf = NibblePath.decode_with_type(data[0]) if is_leaf: return Node.Leaf(path, data[1]) else: ref = _prepare_reference_for_usage(data[1]) return Node.Extension(path, ref) def into_reference(node): #    . #      32 , #   -   . #       . encoded_node = node.encode() if len(encoded_node) < 32: return encoded_node else: return keccak_hash(encoded_node)

休息一下


！ 有很多信息。 我认为是时候放松一下了。 这是另一只为您服务的猫：


你可以在休息时间吃点东西


米洛塔，对不对？ 好，回到我们的树上。


默克尔·帕特里夏·特里


华友世纪-辅助元素已经准备好，我们传递给最美味的。 以防万一，我会提醒我们树的界面。 同时，我们实现了__init__方法。


 class MerklePatriciaTrie: def __init__(self, storage, root=None): self._storage = storage self._root = root def root(self): pass def get(self, encoded_key): pass def update(self, encoded_key, encoded_value): pass def delete(self, encoded_key): pass

但是，对于其余方法，我们将一一处理。


得到


get方法（原则上与其他方法一样）将由两部分组成。 该方法本身将准备数据并将结果带入预期的形式，而实际工作将在辅助方法内部进行。


基本方法非常简单：


 class MerklePatriciaTrie: # ... def get(self, encoded_key): if not self._root: raise KeyError path = NibblePath(encoded_key) #       #  ,    ,    . result_node = self._get(self._root, path) if type(result_node) is Node.Extension or len(result_node.data) == 0: raise KeyError return result_node.data

但是， _get并不复杂：为了到达所需的节点，我们需要从根目录转到整个提供的路径。 如果最后我们找到一个包含数据的节点（叶或分支）-欢呼声，则接收到数据。 如果无法通过，则树中缺少必需的密钥。


实现方式：


 class MerklePatriciaTrie: # ... def _get(self, node_ref, path): #      . node = self._get_node(node_ref) #    --   . #   ,      . if len(path) == 0: return node if type(node) is Node.Leaf: #     Leaf-,     , #      . if node.path == path: return node elif type(node) is Node.Extension: #    -- Extension,    . if path.starts_with(node.path): rest_path = path.consume(len(node.path)) return self._get(node.next_ref, rest_path) elif type(node) is Node.Branch: #    -- Branch,     . #   ,           #  :      . branch = node.branches[path.at(0)] if len(branch) > 0: return self._get(branch, path.consume(1)) #    ,        , #     . raise KeyError

好吧，与此同时，我们将编写用于保存和加载节点的方法。 它们很简单：


 class MerklePatriciaTrie: # ... def _get_node(self, node_ref): raw_node = None if len(node_ref) == 32: raw_node = self._storage[node_ref] else: raw_node = node_ref return Node.decode(raw_node) def _store_node(self, node): reference = Node.into_reference(node) if len(reference) == 32: self._storage[reference] = node.encode() return reference

更新


update方法已经更加有趣了。 只需进行最后操作，然后插入“叶子”节点就不会总是成功。 密钥分离点可能在已保存的Leaf或Extension节点内的某个位置。 在这种情况下，您必须将它们分开并创建几个新节点。


通常，所有逻辑都可以通过以下规则描述：


  1. 当路径与现有节点完全重合时，我们递归地下降树。
  2. 如果路径已完成，并且我们位于“分支”或“叶子”节点中，则意味着update只会更新与此键对应的值。
  3. 如果路径被分割（也就是说，我们不更新值，而是插入一个新值），并且位于“分支”节点中-创建一个“叶子”节点并在相应的分支“分支”分支中指定指向该节点的链接。
  4. 如果路径被划分并且位于“叶子”或“扩展”节点中，则需要创建一个“分支”节点来分隔路径，并在必要时创建用于路径公共部分的“扩展”节点。

让我们逐步用代码表达这一点。 为什么逐渐？ 由于该方法很大，因此很难全面理解它。
但是，我将在此处保留完整方法的链接。


 class MerklePatriciaTrie: # ... def update(self, encoded_key, encoded_value): path = NibblePath(encoded_key) result = self._update(self._root, path, encoded_value) self._root = result def _update(self, node_ref, path, value): #       (,   ), #       . if not node_ref: return self._store_node(Node.Leaf(path, value)) #          #    . node = self._get_node(node_ref) if type(node) == Node.Leaf: ... elif type(node) == Node.Extension: ... elif type(node) == Node.Branch: ...

通用逻辑不够多，最有趣的是if s内部。


if type(node) == Node.Leaf

首先，让我们处理Leaf节点。 它们只有两种情况：


  1. 我们遵循的其余路径与“叶子”节点中存储的路径完全相同。 在这种情况下，我们只需要更改值，保存新节点并返回指向它的链接即可。


  2. 路径是不同的。
    在这种情况下，您需要创建一个将两个路径分开的分支节点。
    如果路径之一为空，则其值将直接传输到分支节点。
    否则，我们将必须创建两个Leaf节点，这些节点的长度缩短了路径的公共部分的长度+ 1个半字节（此半字节将由Branch节点相应分支的索引指示）。



您还需要检查路径中是否存在公共部分，以了解我们是否也需要创建一个扩展节点。


在代码中，它将如下所示：


 if type(node) == Node.Leaf: if node.path == path: #  .       . node.data = value return self._store_node(node) #    . #    . common_prefix = path.common_prefix(node.path) #      . path.consume(len(common_prefix)) node.path.consume(len(common_prefix)) #  Branch . branch_reference = self._create_branch_node(path, value, node.path, node.data) # ,    Extension-. if len(common_prefix) != 0: return self._store_node(Node.Extension(common_prefix, branch_reference)) else: return branch_reference

_create_branch_node过程如下：


 def _create_branch_node(self, path_a, value_a, path_b, value_b): #    Branch-. branches = [b''] * 16 # ,     Branch- . branch_value = b'' if len(path_a) == 0: branch_value = value_a elif len(path_b) == 0: branch_value = value_b #    Leaf-,  . self._create_branch_leaf(path_a, value_a, branches) self._create_branch_leaf(path_b, value_b, branches) #  Branch-     . return self._store_node(Node.Branch(branches, branch_value)) def _create_branch_leaf(self, path, value, branches): # ,     Leaf-. if len(path) > 0: #    ( ). idx = path.at(0) #  Leaf-   ,     . leaf_ref = self._store_node(Node.Leaf(path.consume(1), value)) branches[idx] = leaf_ref

if type(node) == Node.Extension

在扩展节点的情况下，所有内容看起来都像叶子节点。


  1. 如果来自“扩展”节点的路径是我们路径的前缀，那么我们只需递归继续。


  2. 否则，如上所述，我们需要使用Branch节点进行分离。



因此，代码：


 elif type(node) == Node.Extension: if path.starts_with(node.path): #         . new_reference = \ self._update(node.next_ref, path.consume(len(node.path)), value) return self._store_node(Node.Extension(node.path, new_reference)) #  Extension-. #     . common_prefix = path.common_prefix(node.path) #  . path.consume(len(common_prefix)) node.path.consume(len(common_prefix)) #  Branch- ,  ,    . branches = [b''] * 16 branch_value = value if len(path) == 0 else b'' #     Leaf-  Extension- . self._create_branch_leaf(path, value, branches) self._create_branch_extension(node.path, node.next_ref, branches) branch_reference = self._store_node(Node.Branch(branches, branch_value)) # ,    Extension-. if len(common_prefix) != 0: return self._store_node(Node.Extension(common_prefix, branch_reference)) else: return branch_reference

_create_branch_extension过程_create_branch_extension逻辑上等效于_create_branch_leaf过程，但可与扩展节点一起使用。


if type(node) == Node.Branch

但是对于分支节点，一切都很简单。 如果路径为空，则只需将新值保存在当前“分支”节点中。 如果路径不为空，则我们从该路径“咬住”一个半字节，然后递归地向下移动。


我认为该代码不需要注释。


 elif type(node) == Node.Branch: if len(path) == 0: return self._store_node(Node.Branch(node.branches, value)) idx = path.at(0) new_reference = self._update(node.branches[idx], path.consume(1), value) node.branches[idx] = new_reference return self._store_node(node)

删除


！ 最后一种方法仍然存在。 他是最开朗的。 删除的复杂性在于，如果我们完成了整个update链（不包括已删除的键），则需要将结构返回到该结构所处的状态。


, , , , . "", , .


. , N- , N+1 . enum — DeleteAction , .


delete :


 class MerklePatriciaTrie: # ... # Enum, ,         . class _DeleteAction(Enum): #    . #     , #        (_DeleteAction, None). DELETED = 1, #    (,    ). #     ,    #    : (_DeleteAction, ___). UPDATED = 2, #    Branch-  .   -- #    : # (_DeleteAction, (___, ___)) USELESS_BRANCH = 3 def delete(self, encoded_key): if self._root is None: return path = NibblePath(encoded_key) action, info = self._delete(self._root, path) if action == MerklePatriciaTrie._DeleteAction.DELETED: #   . self._root = None elif action == MerklePatriciaTrie._DeleteAction.UPDATED: #   . new_root = info self._root = new_root elif action == MerklePatriciaTrie._DeleteAction.USELESS_BRANCH: #   . _, new_root = info self._root = new_root def _delete(self, node_ref, path): node = self._get_node(node_ref) if type(node) == Node.Leaf: pass elif type(node) == Node.Extension: pass elif type(node) == Node.Branch: pass

, get update . . .


if type(node) == Node.Leaf


. . — , , .


:


 if type(node) == Node.Leaf: if path == node.path: return MerklePatriciaTrie._DeleteAction.DELETED, None else: raise KeyError

, "" — . , . .


if type(node) == Node.Extension


C Extension- :


  1. , Extension- . — .
  2. _delete , "" .
  3. . :

  • . .
  • . .
  • Branch-. . , Branch- . , , Leaf-. — Extension-.

:


 elif type(node) == Node.Extension: if not path.starts_with(node.path): raise KeyError #   . #       . action, info = self._delete(node.next_ref, path.consume(len(node.path))) if action == MerklePatriciaTrie._DeleteAction.DELETED: return action, None elif action == MerklePatriciaTrie._DeleteAction.UPDATED: #    ,     . child_ref = info new_ref = self._store_node(Node.Extension(node.path, child_ref)) return action, new_ref elif action == MerklePatriciaTrie._DeleteAction.USELESS_BRANCH: #     Branch-. stored_path, stored_ref = info # ,     Branch-. child = self._get_node(stored_ref) new_node = None if type(child) == Node.Leaf: #  branch-  . #     Leaf-  Extension. path = NibblePath.combine(node.path, child.path) new_node = Node.Leaf(path, child.data) elif type(child) == Node.Extension: #  Branch-  Extension-. #       . path = NibblePath.combine(node.path, child.path) new_node = Node.Extension(path, child.next_ref) elif type(child) == Node.Branch: #  Branch-      Branch-. #    Extension-    . path = NibblePath.combine(node.path, stored_path) new_node = Node.Extension(path, stored_ref) new_reference = self._store_node(new_node) return MerklePatriciaTrie._DeleteAction.UPDATED, new_reference

if type(node) == Node.Branch


.


, . Branch-, …


怎么了 Branch- Leaf- ( ) Extension- ( ).
, . , — Leaf-. — Extension-. , , 2 — Branch- .


? :


:


  1. , .
  2. , _delete .

:


 elif type(node) == Node.Branch: action = None idx = None info = None if len(path) == 0 and len(node.data) == 0: raise KeyError elif len(path) == 0 and len(node.data) != 0: node.data = b'' action = MerklePatriciaTrie._DeleteAction.DELETED else: #   ,    . #    . idx = path.at(0) if len(node.branches[idx]) == 0: raise KeyError action, info = self._delete(node.branches[idx], path.consume(1)) #  ,   ,  . #      -    #    . node.branches[idx] = b''

_DeleteAction .


  1. Branch- , ( , ). .

 if action == MerklePatriciaTrie._DeleteAction.UPDATED: #   . next_ref = info node.branches[idx] = next_ref reference = self._store_node(node) return MerklePatriciaTrie._DeleteAction.UPDATED, reference elif action == MerklePatriciaTrie._DeleteAction.USELESS_BRANCH: #    . _, next_ref = info node.branches[idx] = next_ref reference = self._store_node(node) return MerklePatriciaTrie._DeleteAction.UPDATED, reference

  1. ( , ), , .

. :


  • . , , , . , .
  • , . Leaf- . .
  • , . , , .
  • , , Branch- . , _DeleteAction — UPDATED .

 if action == MerklePatriciaTrie._DeleteAction.DELETED: non_empty_count = sum(map(lambda x: 1 if len(x) > 0 else 0, node.branches)) if non_empty_count == 0 and len(node.data) == 0: # Branch- ,  . return MerklePatriciaTrie._DeleteAction.DELETED, None elif non_empty_count == 0 and len(node.data) != 0: #  ,   . path = NibblePath([]) reference = self._store_node(Node.Leaf(path, node.data)) return MerklePatriciaTrie._DeleteAction.USELESS_BRANCH, (path, reference) elif non_empty_count == 1 and len(node.data) == 0: #  ,   . return self._build_new_node_from_last_branch(node.branches) else: #  1+   ,  2+ . # Branch-  ,   - UPDATED. reference = self._store_node(node) return MerklePatriciaTrie._DeleteAction.UPDATED, reference

_build_new_node_from_last_branch .


— Leaf Extension, , .


— Branch, Extension , , Branch.


 def _build_new_node_from_last_branch(self, branches): #    . idx = 0 for i in range(len(branches)): if len(branches[i]) > 0: idx = i break #     . prefix_nibble = NibblePath([idx], offset=1) #     child = self._get_node(branches[idx]) path = None node = None #   . if type(child) == Node.Leaf: path = NibblePath.combine(prefix_nibble, child.path) node = Node.Leaf(path, child.data) elif type(child) == Node.Extension: path = NibblePath.combine(prefix_nibble, child.path) node = Node.Extension(path, child.next_ref) elif type(child) == Node.Branch: path = prefix_nibble node = Node.Extension(path, branches[idx]) #  . reference = self._store_node(node) return MerklePatriciaTrie._DeleteAction.USELESS_BRANCH, (path, reference)

其余的


. , … root .


在这里：


 class MerklePatriciaTrie: # ... def root(self): return self._root

, .


… . , , Ethereum . , , , . , :)


, , pip install -U eth_mpt — .


所有人！


结果


?


, -, , - , , . — , .


-, , , — . , skip list interval tree, — , , .


-, , . , - .


-, — .


, , — !



: 1 , 2 , 3 . ! , .

Source: https://habr.com/ru/post/zh-CN446558/

More articles:


All Articles