我们已经讨论了PostgreSQL
索引引擎 ，
访问方法的接口以及三种方法：
哈希索引 ，
B树和
GiST 。 在本文中，我们将描述SP-GiST。
SP-GiST
首先，关于这个名字的几句话。 “ GiST”部分暗示了与同名访问方法的相似之处。 确实存在相似之处：两者都是通用的搜索树，它们提供了用于构建各种访问方法的框架。
“ SP”代表空间分区。 这里的空间通常就是我们用来称呼空间的东西，例如二维平面。 但是我们会看到，任何搜索空间都是指，实际上是任何值域。
SP-GiST适用于可以将空间递归划分
为非相交区域的结构。 此类包括四叉树，k维树（kD树）和基数树。
结构形式
因此，SP-GiST访问方法的思想是将值域拆分
为非重叠的子域，每个子域又可以拆分。 像这样的分区会引起
不平衡的树（不像B树和常规的GiST）。
不相交的特性简化了插入和搜索过程中的决策。 另一方面，通常，诱导的树木是低分支的。 例如，四叉树的一个节点通常具有四个子节点（与B树不同，后者的节点数为数百），并且深度更大。 像这样的树很适合RAM中的工作，但是索引存储在磁盘上，因此，为了减少I / O操作的数量，必须将节点打包到页面中，而有效地做到这一点并不容易。 此外，由于分支深度的差异，在索引中找到不同值所花费的时间可能会有所不同。
此访问方法与GiST一样，可处理低级任务（同时访问和锁定，日志记录和纯搜索算法），并提供专门的简化接口，以增加对新数据类型和新分区算法的支持。
SP-GiST树的内部节点存储对子节点的引用； 可以为每个参考定义
标签 。 此外，内部节点可以存储一个称为
prefix的值。 实际上，该值不是必须的前缀； 它可以被视为所有子节点都满足的任意谓词。
SP-GiST的叶节点包含索引类型的值和对表行（TID）的引用。 索引数据本身（搜索关键字）可以用作值，但不是强制性的：可以存储缩短的值。
此外，叶节点可以分组为列表。 因此，内部节点不仅可以引用一个值，而且可以引用整个列表。
请注意，叶节点中的前缀，标签和值具有各自独立的数据类型。
与GiST中相同，定义搜索的主要功能是
一致性功能 。 该函数针对树节点进行调用，并返回其值与搜索谓词“一致”的一组子节点（通常，形式为“
索引字段运算符表达式 ”）。 对于叶节点，一致性函数确定该节点中的索引值是否满足搜索谓词。
搜索从根节点开始。 一致性功能允许找出有意义的子节点。 对找到的每个节点重复该算法。 搜索是深度优先的。
在物理级别，从I / O操作的角度来看，索引节点被打包到页面中以使节点高效工作。 请注意，一个页面可以包含内部或叶节点，但不能同时包含两者。
示例：四叉树
四叉树用于索引平面中的点。 一个想法是相对于
中心点将区域递归地分为四个部分（象限）。 这样一棵树的分支深度可以变化，并取决于适当象限中点的密度。
这是图中所示的样子，例如通过示例
数据库的示例，该
示例数据库由来自
openflights.org站点的机场
扩充 。 顺便说一下，最近我们发布了该数据库的新版本，在其余版本中，我们用一个“点”类型的字段替换了经度和纬度。
首先，我们将飞机分为四个象限...
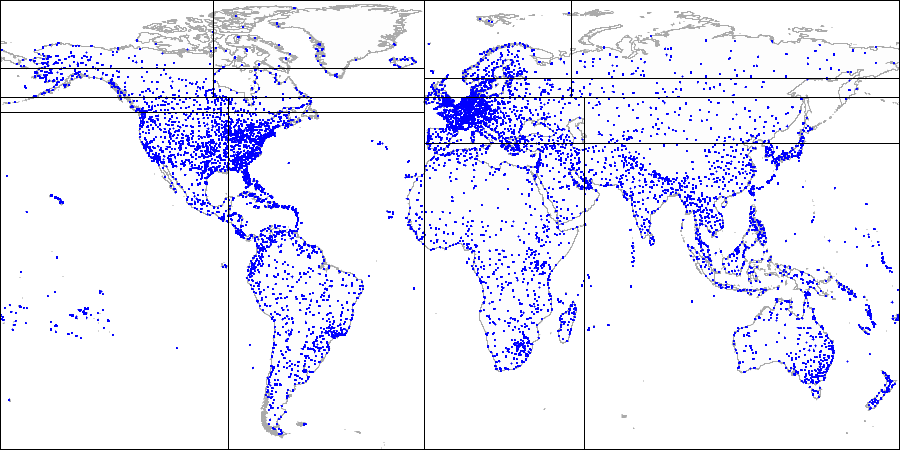然后我们分割每个象限...
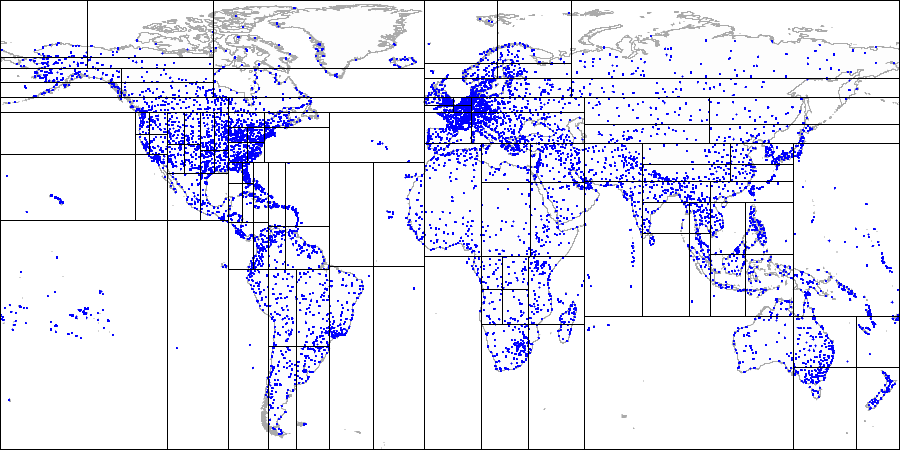依此类推，直到获得最终分区。让我们提供一个
有关GiST相关文章中已经考虑过的简单示例的更多详细信息。 查看这种情况下的分区外观：
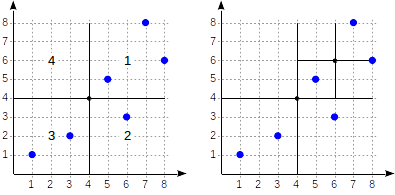
象限的编号如第一个图所示。 为了确定起见，让我们从左到右完全按照相同的顺序放置子节点。 下图显示了这种情况下可能的索引结构。 每个内部节点最多引用四个子节点。 如图所示，每个参考都可以用象限编号标记。 但是在实现中没有标签，因为存储四个引用的固定数组比较方便，其中一些引用可以为空。
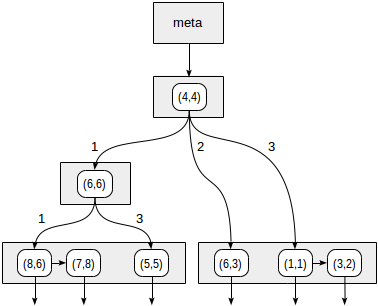
边界上的点与数量较小的象限有关。
postgres=# create table points(p point); postgres=# insert into points(p) values (point '(1,1)'), (point '(3,2)'), (point '(6,3)'), (point '(5,5)'), (point '(7,8)'), (point '(8,6)'); postgres=# create index points_quad_idx on points using spgist(p);
在这种情况下，默认情况下使用“ quad_point_ops”运算符类，其中包含以下运算符：
postgres=# select amop.amopopr::regoperator, amop.amopstrategy from pg_opclass opc, pg_opfamily opf, pg_am am, pg_amop amop where opc.opcname = 'quad_point_ops' and opf.oid = opc.opcfamily and am.oid = opf.opfmethod and amop.amopfamily = opc.opcfamily and am.amname = 'spgist' and amop.amoplefttype = opc.opcintype;
amopopr | amopstrategy -----------------+-------------- <<(point,point) | 1 strictly left >>(point,point) | 5 strictly right ~=(point,point) | 6 coincides <^(point,point) | 10 strictly below >^(point,point) | 11 strictly above <@(point,box) | 8 contained in rectangle (6 rows)
例如，让我们看一下查询如何
select * from points where p >^ point '(2,7)'将执行
select * from points where p >^ point '(2,7)' （查找位于给定点上方的所有点）。
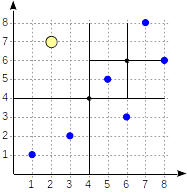
我们从根节点开始，并使用一致性功能选择要下降到的子节点。 对于运算符
>^ ，此函数将点（2,7）与节点（4,4）的中心点进行比较，并选择可能包含所寻找点的象限，在这种情况下为第一象限和第四象限。
在与第一象限相对应的节点中，我们再次使用一致性函数确定子节点。 中心点是（6,6），我们再次需要浏览第一和第四象限。
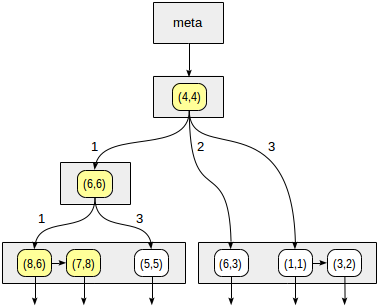
叶节点（8.6）和（7.8）的列表对应于第一象限，其中只有点（7.8）满足查询条件。 对第四象限的引用为空。
在内部节点（4.4）中，对第四象限的引用也为空，从而完成了搜索。
postgres=# set enable_seqscan = off; postgres=# explain (costs off) select * from points where p >^ point '(2,7)';
QUERY PLAN ------------------------------------------------ Index Only Scan using points_quad_idx on points Index Cond: (p >^ '(2,7)'::point) (2 rows)
内部构造
我们可以使用前面提到的“
gevel ”扩展名来探索SP-GiST索引的内部结构。 坏消息是，由于存在错误，此扩展程序无法在现代PostgreSQL版本中正常工作。 好消息是，我们计划通过“ gevel”（
讨论 ）功能增强“ pageinspect”。 该错误已在“ pageinspect”中修复。
再次，坏消息是该补丁没有进展。
例如，让我们使用扩展的演示数据库，该数据库用于用世界地图绘制图片。
demo=# create index airports_coordinates_quad_idx on airports_ml using spgist(coordinates);
首先，我们可以获得索引的一些统计信息：
demo=# select * from spgist_stats('airports_coordinates_quad_idx');
spgist_stats ---------------------------------- totalPages: 33 + deletedPages: 0 + innerPages: 3 + leafPages: 30 + emptyPages: 2 + usedSpace: 201.53 kbytes+ usedInnerSpace: 2.17 kbytes + usedLeafSpace: 199.36 kbytes+ freeSpace: 61.44 kbytes + fillRatio: 76.64% + leafTuples: 5993 + innerTuples: 37 + innerAllTheSame: 0 + leafPlaceholders: 725 + innerPlaceholders: 0 + leafRedirects: 0 + innerRedirects: 0 (1 row)
其次，我们可以输出索引树本身：
demo=# select tid, n, level, tid_ptr, prefix, leaf_value from spgist_print('airports_coordinates_quad_idx') as t( tid tid, allthesame bool, n int, level int, tid_ptr tid, prefix point,
tid | n | level | tid_ptr | prefix | leaf_value ---------+---+-------+---------+------------------+------------------ (1,1) | 0 | 1 | (5,3) | (-10.220,53.588) | (1,1) | 1 | 1 | (5,2) | (-10.220,53.588) | (1,1) | 2 | 1 | (5,1) | (-10.220,53.588) | (1,1) | 3 | 1 | (5,14) | (-10.220,53.588) | (3,68) | | 3 | | | (86.107,55.270) (3,70) | | 3 | | | (129.771,62.093) (3,85) | | 4 | | | (57.684,-20.430) (3,122) | | 4 | | | (107.438,51.808) (3,154) | | 3 | | | (-51.678,64.191) (5,1) | 0 | 2 | (24,27) | (-88.680,48.638) | (5,1) | 1 | 2 | (5,7) | (-88.680,48.638) | ...
但是请记住，“ spgist_print”不输出所有叶值，而是仅输出列表中的第一个叶值，因此显示的是索引的结构，而不是其全部内容。
示例：k维树
对于平面中的相同点，我们还可以建议另一种划分空间的方法。
让我们通过被索引的第一个点画
一条水平线 。 它将平面分为两部分：上部和下部。 要索引的第二点属于这些部分之一。 至此，让我们画
一条垂直线 ，将这部分分为两部分：右和左。 我们再次通过下一个点绘制一条水平线，并通过下一个点绘制一条垂直线，依此类推。
以这种方式构建的树的所有内部节点将只有两个子节点。 这两个引用中的每一个都可以指向层次结构中下一个内部节点或叶节点列表。
这种方法可以很容易地推广到k维空间，因此，这些树在文献中也称为k维（kD树）。
通过机场示例说明方法：
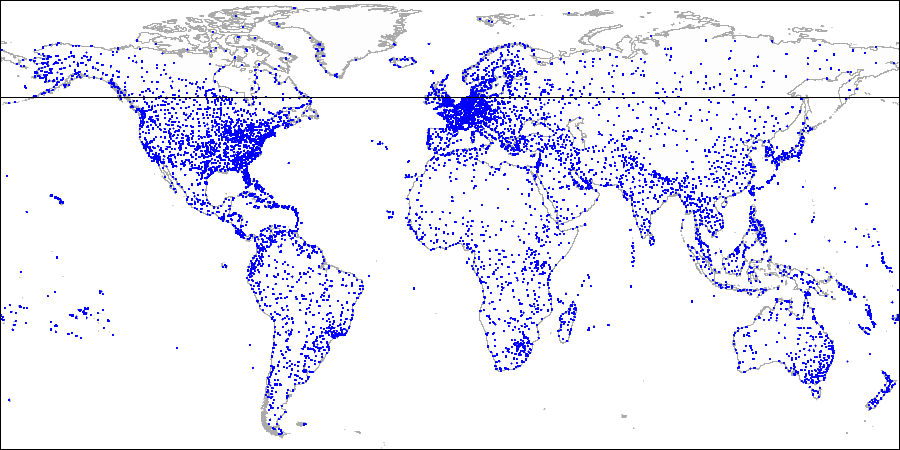首先，我们将飞机分为上下两部分...
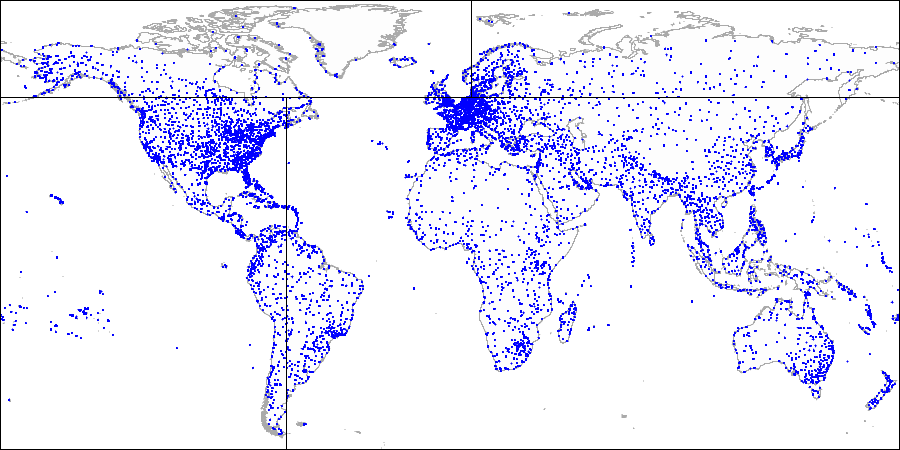然后我们将每个部分分成左右两部分...
依此类推，直到获得最终分区。要像这样使用分区，我们需要在创建索引时明确指定运算符类
“ kd_point_ops” 。
postgres=# create index points_kd_idx on points using spgist(p kd_point_ops);
该类包含与“默认”类“ quad_point_ops”完全相同的运算符。
内部构造
在浏览树结构时，我们需要考虑到在这种情况下，前缀只是一个坐标而不是一个点：
demo=# select tid, n, level, tid_ptr, prefix, leaf_value from spgist_print('airports_coordinates_kd_idx') as t( tid tid, allthesame bool, n int, level int, tid_ptr tid, prefix float,
tid | n | level | tid_ptr | prefix | leaf_value ---------+---+-------+---------+------------+------------------ (1,1) | 0 | 1 | (5,1) | 53.740 | (1,1) | 1 | 1 | (5,4) | 53.740 | (3,113) | | 6 | | | (-7.277,62.064) (3,114) | | 6 | | | (-85.033,73.006) (5,1) | 0 | 2 | (5,12) | -65.449 | (5,1) | 1 | 2 | (5,2) | -65.449 | (5,2) | 0 | 3 | (5,6) | 35.624 | (5,2) | 1 | 3 | (5,3) | 35.624 | ...
示例：基数树
我们还可以使用SP-GiST为字符串实现基数树。 基数树的想法是要索引的字符串没有完全存储在叶节点中，而是通过将存储在该节点上方的节点中的值连接到根来获得的。
假设，我们需要索引站点URL：“ postgrespro.ru”，“ postgrespro.com”，“ postgresql.org”和“ planet.postgresql.org”。
postgres=# create table sites(url text); postgres=# insert into sites values ('postgrespro.ru'),('postgrespro.com'),('postgresql.org'),('planet.postgresql.org'); postgres=# create index on sites using spgist(url);
该树将如下所示：
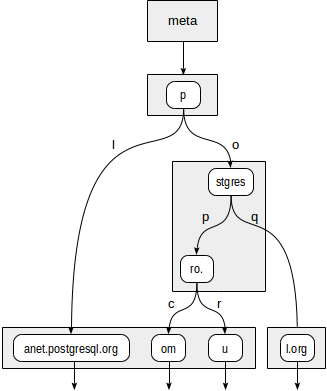
树的内部节点存储所有子节点共有的前缀。 例如，在“ stgres”的子节点中，值以“ p” +“ o” +“ stgres”开头。
与四叉树不同，指向子节点的每个指针都另外用一个字符标记（更确切地说，用两个字节标记，但这并不重要）。
“ Text_ops”运算符类支持B树形运算符：“ equal”，“ greater”和“ less”：
postgres=# select amop.amopopr::regoperator, amop.amopstrategy from pg_opclass opc, pg_opfamily opf, pg_am am, pg_amop amop where opc.opcname = 'text_ops' and opf.oid = opc.opcfamily and am.oid = opf.opfmethod and amop.amopfamily = opc.opcfamily and am.amname = 'spgist' and amop.amoplefttype = opc.opcintype;
amopopr | amopstrategy -----------------+-------------- ~<~(text,text) | 1 ~<=~(text,text) | 2 =(text,text) | 3 ~>=~(text,text) | 4 ~>~(text,text) | 5 <(text,text) | 11 <=(text,text) | 12 >=(text,text) | 14 >(text,text) | 15 (9 rows)
带波浪号的运算符的区别在于，它们操作
字节而不是
字符 。
有时，以基数树的形式表示的结果可能会比B树要紧凑得多，因为这些值没有完全存储，而是随着在树中下降时的需要而重建的。
考虑一个查询：
select * from sites where url like 'postgresp%ru' 。 可以使用索引执行：
postgres=# explain (costs off) select * from sites where url like 'postgresp%ru';
QUERY PLAN ------------------------------------------------------------------------------ Index Only Scan using sites_url_idx on sites Index Cond: ((url ~>=~ 'postgresp'::text) AND (url ~<~ 'postgresq'::text)) Filter: (url ~~ 'postgresp%ru'::text) (3 rows)
实际上，索引用于查找大于或等于“ postgresp”但小于“ postgresq”的值（索引条件），然后从结果中选择匹配的值（过滤器）。
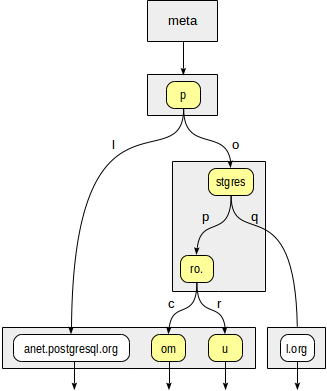
首先，一致性函数必须确定我们需要下降到“ p”根的哪些子节点。 有两个选项：“ p” +“ l”（无需下降，即使不深入潜水也很清楚）和“ p” +“ o” +“ stgres”（继续下降）。
对于“ stgres”节点，再次需要调用一致性函数以检查“ postgres” +“ p” +“ ro”。 （继续下降）和“ postgres” +“ q”（无需下降）。
为“ ro”。 节点及其所有子叶节点，一致性函数将响应“是”，因此index方法将返回两个值：“ postgrespro.com”和“ postgrespro.ru”。 在过滤阶段将选择一个匹配值。
内部构造
在浏览树结构时，我们需要考虑数据类型：
postgres=# select * from spgist_print('sites_url_idx') as t( tid tid, allthesame bool, n int, level int, tid_ptr tid, prefix text,
物产
让我们看一下SP-GiST访问方法的属性（
先前提供了查询）：
amname | name | pg_indexam_has_property --------+---------------+------------------------- spgist | can_order | f spgist | can_unique | f spgist | can_multi_col | f spgist | can_exclude | t
SP-GiST索引不能用于排序和支持唯一性约束。 此外，不能在几列上创建类似这样的索引（与GiST不同）。 但是允许使用此类索引来支持排除约束。
以下索引层属性可用：
name | pg_index_has_property ---------------+----------------------- clusterable | f index_scan | t bitmap_scan | t backward_scan | f
与GiST的区别在于，不可能进行聚类。
最终，以下是列层属性：
name | pg_index_column_has_property --------------------+------------------------------ asc | f desc | f nulls_first | f nulls_last | f orderable | f distance_orderable | f returnable | t search_array | f search_nulls | t
不支持排序，这是可以预测的。 到目前为止，SP-GiST中不提供用于搜索最近邻居的距离运算符。 很有可能将来会支持此功能。
Nikita Glukhov将在即将发布的PostgreSQL 12中对它进行支持。
SP-GiST可用于仅索引扫描，至少用于所讨论的操作符类。 如我们所见，在某些情况下，索引值显式存储在叶节点中，而在另一些情况下，索引值在树下降过程中被部分地重建。
空值
为了使图片复杂化，到目前为止，我们还没有提到NULL。 从索引属性可以明显看出，它支持NULL。 真的：
postgres=# explain (costs off) select * from sites where url is null;
QUERY PLAN ---------------------------------------------- Index Only Scan using sites_url_idx on sites Index Cond: (url IS NULL) (2 rows)
但是，对于SP-GiST，NULL是陌生的。 “ spgist”运算符类中的所有运算符都必须严格：每当运算符的任何参数为NULL时，运算符都必须返回NULL。 该方法本身确保了这一点：NULL仅不传递给运算符。
但是要将访问方法用于仅索引扫描，无论如何都必须将NULL存储在索引中。 它们被存储，但是存储在具有其自身根的单独树中。
其他数据类型
除了字符串的点和基数树以外，还基于PostgreSQL实现了其他基于SP-GiST的方法：
- Box_ops运算符类为矩形提供四叉树。
每个矩形都由一个四维空间中的一个点表示，因此，象限数等于16。当矩形的交点很多时，这样的索引在性能上可以击败GiST：在GiST中，无法绘制边界从而使相交的对象彼此分离，而点（甚至是四维）不存在此类问题。
- “ Range_ops”运算符类提供间隔的四叉树。
间隔由二维点表示 ：下边界为横坐标，上边界为纵坐标。
继续阅读 。