Geekly articles weekly

我们为确定电磁波到达方向的MUSIC算法建模

野猫


前言


我将从远处开始介绍。 曾几何时，在遥远的2016-2017年，您谦虚的仆人设法在遥远的伊尔默瑙 （德国）进行了为期六个月的培训课程，在那里他成功地（总体上）成功完成了硕士课程通信和信号处理 。 该程序不是一个容易的程序，但是现在，使它恢复起来甚至很愉快。 有时候...


因此，在培训结束时，除了文凭，我手上还有很多材料，我认为不共享是错误的。


这些材料之一就在您眼前。


准备研讨会时我追求什么目标 ：


  1. 在天线阵列主题中谈论一些已经建立的“智能”方法，该方法最容易使用，并且用俄语进行；
  2. 在Python 3中进行一次小型仿真，以激起无线电工程师们对编程语言的进一步了解（如果您尚未仔细研究的话）；
  3. 提供指向优秀英语文献的链接-现在，without，无处可去，而无需阅读外国资源。

注意事项 ：


  • MUSIC方法（多重信号分类）-实际上是指预览。

可以在此处找到图表形成和MVDR方法的示例（如果对其他材料有疑问或建议，可以在Github.Gist上继续进行讨论）。

如上所述，我们将使用Python，即：


import numpy as np import matplotlib.pyplot as plt

您为什么不问MATLAB，它是线性代数建模的最流行，最方便的候选人之一？ 因为，我想证明类似的工作可以在Python中完成，并且Python的范围比MATLAB的范围要广得多。 因此，在我看来，熟悉Python语法是一件有用的事情。


让我们开始吧！


公式是通过https://upmath.me/准备的。 感谢创作者提供的出色工具！

问题陈述


假设有一个线性天线阵列，该阵列由许多彼此隔开的元件组成 \ Delta = \ frac {\ lambda} {2} （天线阵列的步骤），其中 \ lambda -载波电磁（EM）波的长度。


电磁波从不同方向落在该天线阵列上。



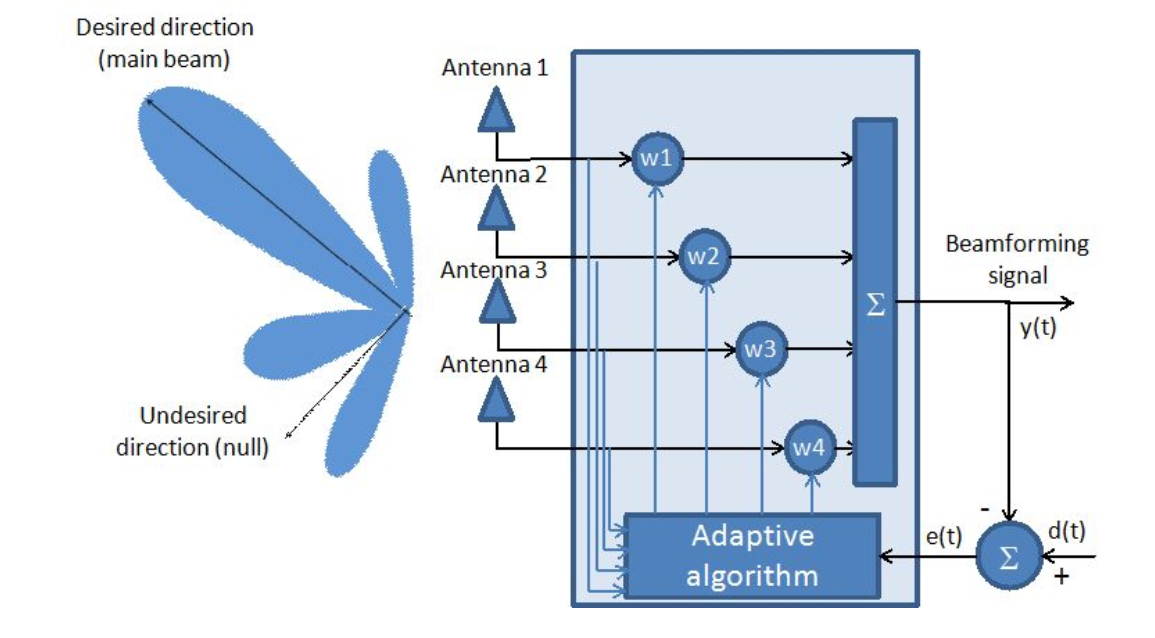
图 1. 自适应天线系统。

从图中可以看出，天线阵列被认为是自适应滤波器。


实际上，找到系数的最佳矢量（ \ mathbf {w} _ {opt} 从数学的角度来看，）是自适应天线阵列的主要任务。


最初，我们不知道信号来自哪个特定方向以及有多少方向。 为了解决这一矛盾，我们将使用MUSIC算法，该算法用于以高分辨率估计空间频率。


接收信号模拟


我们可以通过以下公式表示接收信号的模型：


\ mathbf {X} = \ mathbf {A} \ mathbf {S} + \ mathbf {N}


在哪里 \ mathbf {A} = [\ mathbf {a}（\ theta_1）\ quad \ mathbf {a}（\ theta_2）\ quad ... \ quad \ mathbf {a}（\ theta_d）] -天线阵列的扫描向量（转向向量）的矩阵（ a_i = \ exp（-j \ mu m_i） ， m = 0，1 ...（M-1） ， 中号 -天线阵列的元件数， d -电磁波源的数量， \ theta -倾斜EM波的到达方向）， \ mathbf {S} -传输字符矩阵，以及 \ mathbf {N} -附加噪声矩阵。


ULA
图 2.全向线性天线阵列（ULAA-均匀线性天线阵列）[1，p。 32]。

让我们以“每天”的方式重新考虑这个公式：在网格上，我们从各种信号中得到一些“混乱”，我们用 \ mathbf {X} 。 我们没有明确接收有关源和方向数量的信息，但是，关于此的信息仍然包含在接收到的信号中。


我们开始搜索！


为此，它们通常不进行复杂信号幅度矩阵本身的操作，而是采用其协方差进行操作（即，本质上是使用幂）：


\ mathbf {R} _ {xx} = \ mathbf {X} \ mathbf {X} ^ H = \ mathbf {A} \ mathbf {R} _ {ss} \ mathbf {A} ^ H + \ mathbf {R} _ {nn}


条件


我们介绍一个重要的考虑条件：瑞利角分辨率极限：


sin（\ theta_R）= \ frac {\ lambda} {D}


在哪里 D = M \三角洲 是线性晶格的长度。


我们通过空间频率的概念重新定义电磁波的到达角度：


\ mu_R = \ frac {2 \ pi} {\ lambda} \ Delta sin（\ theta_R）= \ frac {2 \ pi} {\ lambda} \ Delta \ frac {\ lambda} {\ Delta M} = \ frac { 2 \ pi} {M}


在哪里 \ mu_R -光束的主瓣有一个标准宽度（ standard beamwidth ）。


为了检查我们的方法的有效性以及在什么条件下，我们引入一些给定的角度间隔值：


  1. \ mu_1 =-\ mu_R，\ quad \ mu_2 = 0，\ quad \ mu_3 = \ mu_R \ quad -分成一个光束宽度；


  2. \ mu_1 = -0.5 \ mu_R，\ quad \ mu_2 = 0，\ quad \ mu_3 = 0.5 \ mu_R \ quad -划分为一秒的光束宽度；


  3. \ mu_1 = -0.3 \ mu_R，\ quad \ mu_2 = 0，\ quad \ mu_3 = 0.3 \ mu_R \ quad -分成光束宽度的十分之三。



定义输入参数：


 M = 10 #    () SNR = 10 #  - (dB) d = 3 #     N = 50 #  "" (snapshots) S = ( np.sign(np.random.randn(d,N)) + 1j * np.sign(np.random.randn(d,N)) ) / np.sqrt(2) # QPSK W = ( np.random.randn(M,N) + 1j * np.random.randn(M,N) ) / np.sqrt(2) * 10**(-SNR/20) # AWGN #  : # sqrt(N0/2)*(G1 + jG2), #  G1  G2 -   . # .. Es( )  QPSK  1 ,    (noise spectral density): # N0 = (Es/N)^(-1) = SNR^(-1) [] (   ,  SNR = Es/N0); #    : # SNR_dB = 10log10(SNR) => N0_dB = -10log10(SNR) = -SNR_dB []; #    SNR    (..  ),   : # SNR = 10^(SNR_dB/10) => sqrt(N0) = (10^(-SNR_dB/10))^(1/2) = 10^(-SNR_dB/20) mu_R = 2*np.pi / M

关于方法本身的一些理论


首先，我们注意到MUSIC方法的前身是Pisarenko方法（1973年）。 Pisarenko方法的考虑问题是估计白噪声中复指数和的频率。 V.F. Pisarenko证明，可以从与自相关矩阵的最小特征值相对应的特征向量中找到频率。 随后，此方法成为MUSIC方法的特例。 [2，p。 459]


Schmidt和他的同事在1979年提出了多信号分类算法（MUSIC）[4]。 该算法的主要方法是将接收信号的协方差矩阵分解为特征值。 由于此算法考虑了不相关的噪声，因此生成的协方差矩阵具有对角线形式。 在此，信号和噪声子空间是使用线性代数计算的，并且彼此正交。 因此，该算法使用正交性来提取信号和噪声子空间[5]。


广义MUSIC算法可以定义如下：


  • 找到协方差矩阵 \ mathbf {R} _ {xx}
  • 通过EVD或其他合适的数值算法查找特征向量：

\ mathbf {R} _ {xx} = \ mathbf {U} \ mathbf {\ Lambda} \ mathbf {U} ^ H \ qquad（1）


  • 通过以下公式找到伪谱（为什么带有伪伪前缀，我们将在下面讨论）：

P_ {MU}（e ^ {j \ omega}）= \ frac {1} {\ sum \ limits_ {i = d + 1} ^ {M} | \ mathbf {a} ^ H \ mathbf {u} _i | ^ 2} \ qquad（2）


在哪里 \ mathbf {a} = \开始{bmatrix} e ^ {j0 \ omega}＆e ^ {j1 \ omega}＆e ^ {j2 \ omega}＆...＆e ^ {j（M-1）\ omega } \ end {bmatrix} ^ T 是在给定范围内的频率ω的指数矢量，并且 \ mathbf {u} _i -与矩阵（1）的噪声子空间相对应的协方差矩阵（1）的第i个特征向量（特征向量）-因此采用 d + 1 （ d 是矩阵（1）的等级。


为了更清晰，请尝试运行reference提供的适当的MATLAB脚本。 注意两点：
  • 作者无需在分母（2）中计算第二范数的平方，而是将FFT算法应用于特征向量，这有助于使用内置函数进行建模，并且从数学的角度来看，通常不与该理论相矛盾；
  • 通过卷积矩阵计算协方差矩阵；上面显示了一种不同的方法来估计空间频率。

正如您可能从名称中猜到的那样，MUSIC还是一种用于估计高分辨率接收方向的经典方法。 在此情况下，用于计算伪光谱的算法如下：


  • 我们找到接收信号的协方差矩阵；


  • 找到零子空间 \ mathbf {U} _0 ：




\ mathbf {U} = [\ mathbf {U} _s \ quad \ mathbf {U} _0]


  • 选择一些搜索范围：

a（\ mu）= \开始{bmatrix} e ^ {j0 \ mu_1}＆...＆e ^ {j0 \ mu_Q} \\ ...＆...＆... \\ e ^ {j（ M-1）\ mu_1}＆...＆e ^ {j（M-1）\ mu_Q} \ end {bmatrix}


在哪里 \ mu =-\ frac {2 \ pi f_c} {c} \ Delta sin \ theta =-\ frac {2 \ pi} {\ lambda} \ Delta sin \ theta


  • 计算伪频谱：

P_ {MU}（\ theta）= \ frac {\ mathbf {a} ^ H（\ theta）\ mathbf {a}（\ theta）} {\ mathbf {a} ^ H（\ theta）\ mathbf {U} _0 \ mathbf {U} _0 ^ H \ mathbf {a}（\ theta）}


表1中描述了频谱分析与EM波的到达角（DoA-到达方向）分析之间的关系。


表1 MUSIC应用程序之间的通信 ：信号阵列处理和谐波搜索[6]。


可变的信号阵列处理谐波搜索
中号
传感器数量时间段数
ñ
时间段数实验次数
d
波前数复杂组件数
\亩
空间频率归一化频率

通常，可以将通过阵列（光栅）的接收过程与经典离散化过程进行比较，因为 实际上，每个接收具有一定相位延迟（即具有一定时间延迟）的波的传感器都执行采样增量脉冲的功能。 经典频谱分析的实现（实验）数量将与时间段（快照）的数量相对应。 每个源都有自己的波前，在频谱分析的情况下，这等于信号的唯一正弦波数。


现在回到计算特征向量的时刻。 我们已经在上面提到了向量 a（\ theta_i）\ epsilon A 在哪里 i = 1,2，..，d 与协方差矩阵的噪声子空间正交，即


a（\ theta_i）^ TU_0 = 0 ^ T


实际上，我们看到了一个方程组，通过求解可以找到其根-特征向量。 与数值算法（如上所述，该算法适用于EVD）相反，这种方法允许人们获得真实的而不是近似的特征值。 这就是为什么这种方法允许我们获得的不是伪频谱，而是频谱。 相同的想法构成了Root MUSIC算法的基础。


造型


！ 最后，对所有公式进行了描述并作了一些解释。 我们可以开始建模了。


 cases = [[-1., 0, 1.], [-0.5, 0, 0.5], [-0.3, 0, 0.3],] for idxm, c in enumerate(cases): #   ( ): mu_1 = c[0]*mu_R mu_2 = c[1]*mu_R mu_3 = c[2]*mu_R #   a_1 = np.exp(1j*mu_1*np.arange(M)) a_2 = np.exp(1j*mu_2*np.arange(M)) a_3 = np.exp(1j*mu_3*np.arange(M)) A = (np.array([a_1, a_2, a_3])).T #    X = np.dot(A,S) + W #    R = np.dot(X,np.matrix(X).H) U, Sigma, Vh = np.linalg.svd(X, full_matrices=True) U_0 = U[:,d:] #   thetas = np.arange(-90,91)*(np.pi/180) #   mus = np.pi*np.sin(thetas) #    a = np.empty((M, len(thetas)), dtype = complex) for idx, mu in enumerate(mus): a[:,idx] = np.exp(1j*mu*np.arange(M)) # MVDR: S_MVDR = np.empty(len(thetas), dtype = complex) for idx in range(np.shape(a)[1]): a_idx = (a[:, idx]).reshape((M, 1)) S_MVDR[idx] = 1 / (np.dot(np.matrix(a_idx).H, np.dot(np.linalg.pinv(R),a_idx))) # MUSIC: S_MUSIC = np.empty(len(thetas), dtype = complex) for idx in range(np.shape(a)[1]): a_idx = (a[:, idx]).reshape((M, 1)) S_MUSIC[idx] = np.dot(np.matrix(a_idx).H,a_idx)\ / (np.dot(np.matrix(a_idx).H, np.dot(U_0,np.dot(np.matrix(U_0).H,a_idx)))) plt.subplots(figsize=(10, 5), dpi=150) plt.semilogy(thetas*(180/np.pi), np.real( (S_MVDR / max(S_MVDR))), color='green', label='MVDR') plt.semilogy(thetas*(180/np.pi), np.real((S_MUSIC/ max(S_MUSIC))), color='red', label='MUSIC') plt.grid(color='r', linestyle='-', linewidth=0.2) plt.xlabel('Azimuth angles θ (degrees)') plt.ylabel('Power (pseudo)spectrum (normalized)') plt.legend() plt.title('Case #'+str(idxm+1)) plt.show()




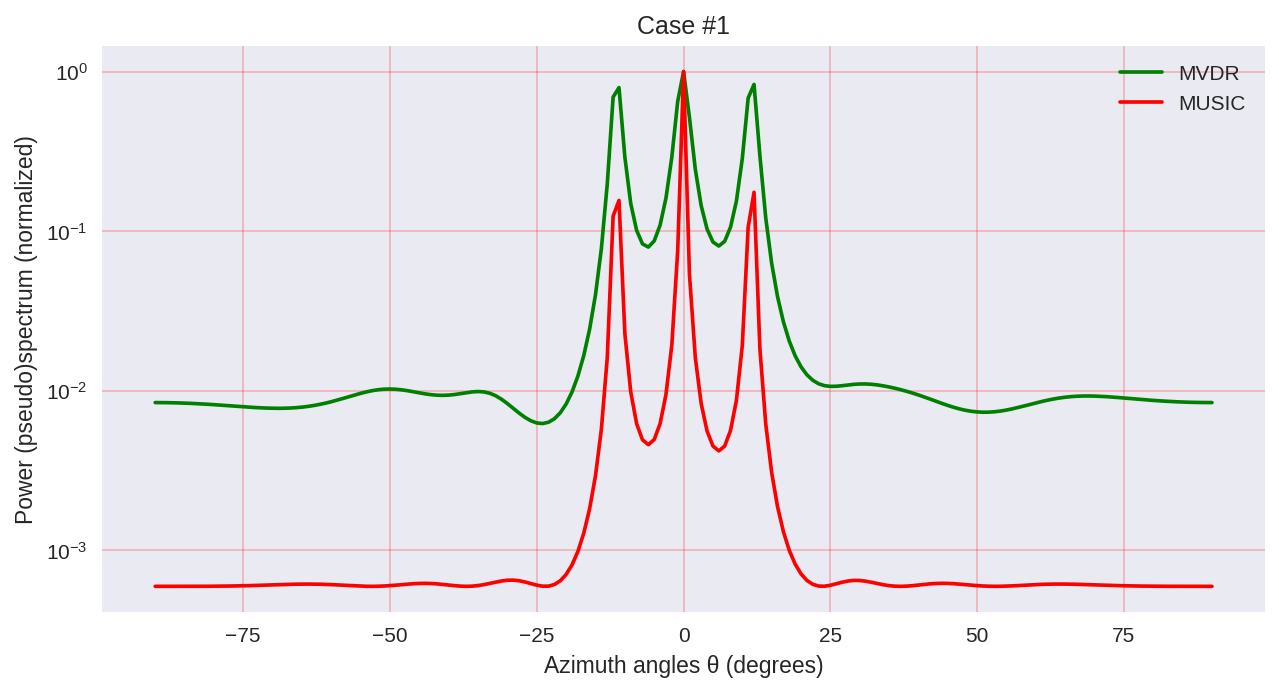
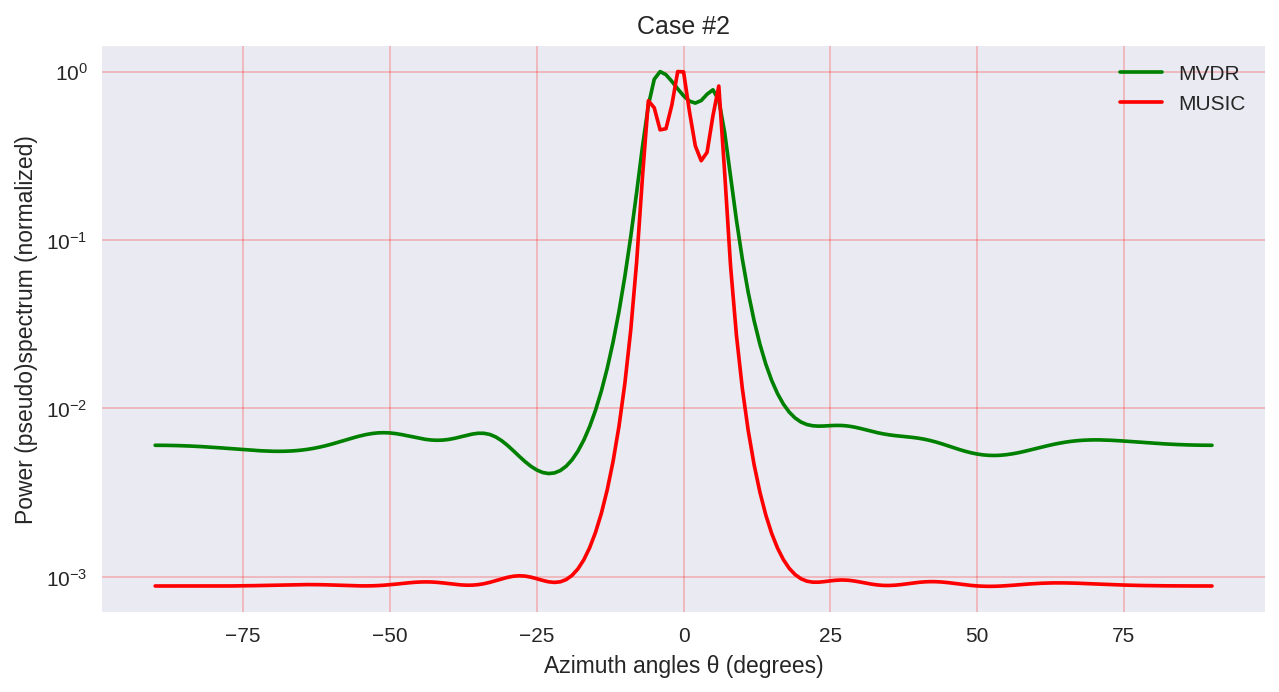
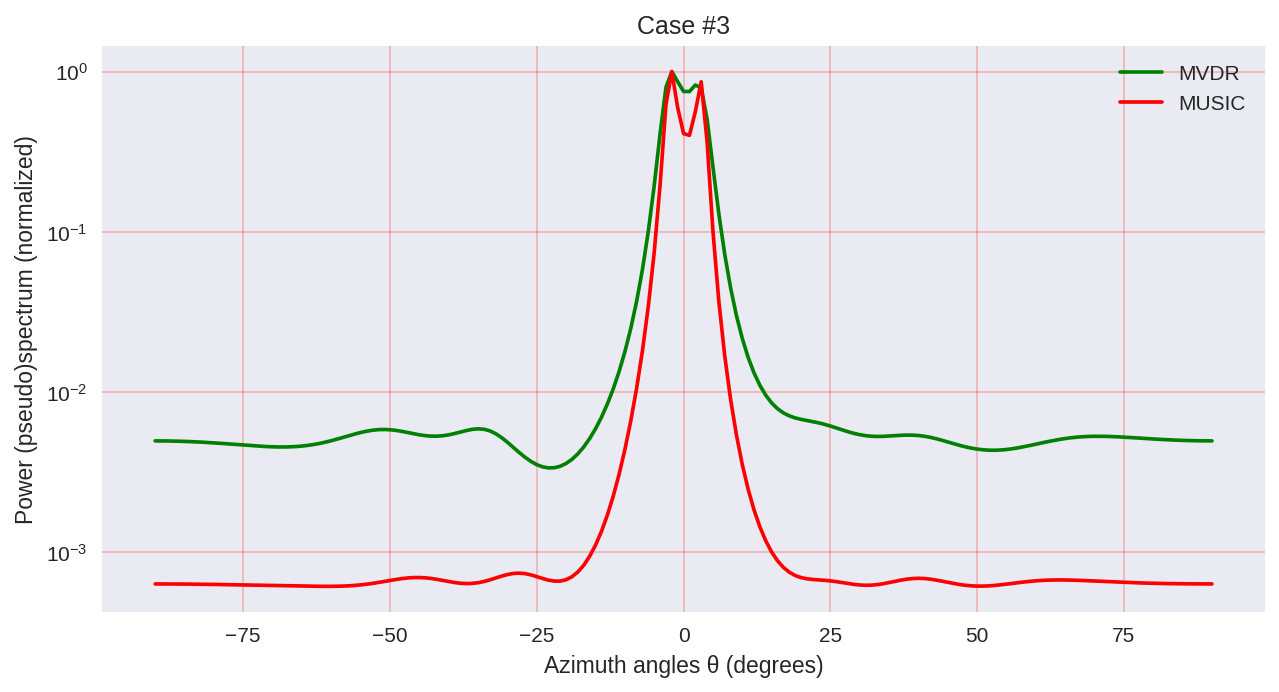
我们可以看到，MUSIC具有更高的分辨率，并且比MVDR所允许的结果总体上更好，例如MVDR可以代表光谱分析的参数化方法。


但是，应该牢记的是，使用MUSIC时，我们会使用计算量更大的算法，例如EVD或SVD，要付出更高的准确性，就要付出一定的代价。


这样的事情。


二手文献清单：


  1. Haykin，Simon和KJ Ray Liu。 阵列处理和传感器网络手册。 卷 63.约翰·威利父子（John Wiley＆Sons），2010年。 102-107
  2. Hayes MH统计数字信号处理和建模。 -约翰·威利父子（John Wiley＆Sons），2009年。
  3. Haykin，SimonS。自适应滤波器理论。 印度Pearson Education，2008年。 422-427
  4. 里士满（Richmond），ChrisD。“ Capon算法均方误差阈值SNR预测和分辨率的可能性。” IEEE Transactions on Signal Processing 53.8（2005）：2748-2764。
  5. SKP Gupta，MUSIC和改进的MUSIC算法以模拟到达的确定性，IEEE，2015年。
  6. 马丁·哈特教授的演讲（ 数组 ）

Source: https://habr.com/ru/post/zh-CN446674/

More articles:


All Articles