有一个水手。 他在不同的港口有两个心爱的女人，他想要孩子-他只是没有决定一两个。 他决定扔硬币。 鹰（Eagle）-其中一名妇女有一个孩子（她首先要去港口工作（这是这样工作的）），尾巴-她将为每个妇女生一个孩子。 还不知道硬币是如何掉落的以及命运如何将硬币扔到世界各地，但您是他的孩子。 您是他唯一的孩子的可能性有多大？
让我们考虑一下。 诚实的硬币给出了这种概率1/2。 但这是如此明显吗？ 毕竟，如果尾巴掉了，那么可以问一个问题的人“你”将是三个：如果鹰掉了，一个孤独的孩子，如果尾巴掉了，两个。 因此，概率为1/3。 不明显吗？ 让我重新提出问题，以便第二个答案更加明显。
睡美人的任务
美女参加了实验：在星期天，实验者秘密地向她投了一个硬币。 如果老鹰掉落，他们将其安乐死，在星期一将其唤醒，然后再次对其进行安乐死。 她在星期三醒来，实验结束了。 如果尾巴掉下来，它们也会在周一将她唤醒，但是随后它们将擦除内存并使它们进入睡眠状态，然后在周二再次醒来。 他们再次安乐死（已经不擦除内存），并且在星期三它们完全醒来。
因此，美感被唤醒（在星期一或星期二）。 他们问她一个问题：您认为今天是星期二的概率是多少？ 硬币是公平的，这意味着概率是1/2。 但是在星期一，她被唤醒的频率是星期二的两倍！ 因此，概率为1/3。
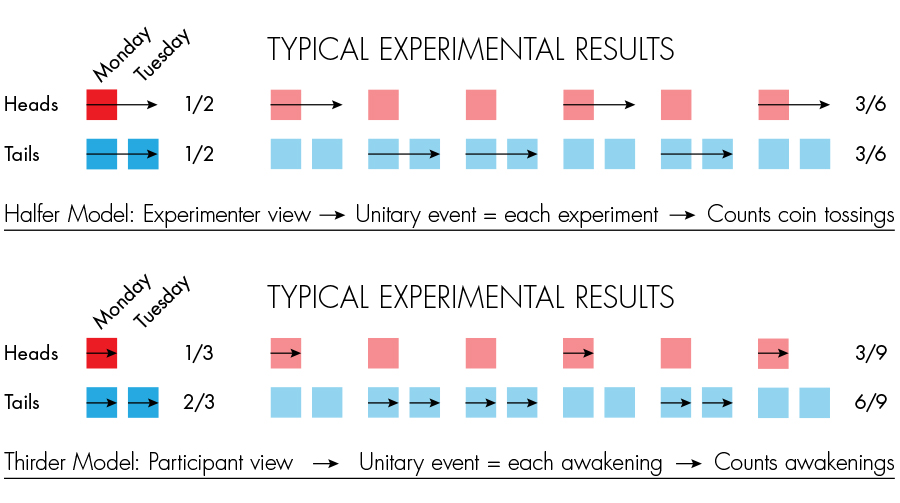在对悖论的描述中，您可以读到这两种解决方案都是正确的，这是正确的，但是兔子洞导致的问题更深。 她拥有两门哲学流派，即
自我抽样假设（SSA）和
自我指示假设（SIA） 。 它用英语编写，因为即使Wiki上的文章本身也仅以英语存在（只有一种语言，这种情况很少见）。 如果您想将这些术语翻译成俄文，请在注释中写上。
自采样假设
SSA听起来是这样的：
在所有条件都相同的情况下，观察者应考虑从他自己已经存在，存在或将要存在的一组观察者中随机选择他。也就是说，SSA的原理是建立在相当合理的基础上的，观察者不应在时间和空间上都认为自己是“被选择的”。 SSA为睡美人的任务给出答案1/2。
让我们通过一个示例来了解SSA的工作方式。 最重要的是，SSA的工作类似于灵魂在随机选择的身体中的
化身 ，并且对于灵魂而言，没有时间（外在主义），并且可以随时化身为身体。 绘制不同时间的世界人口图。
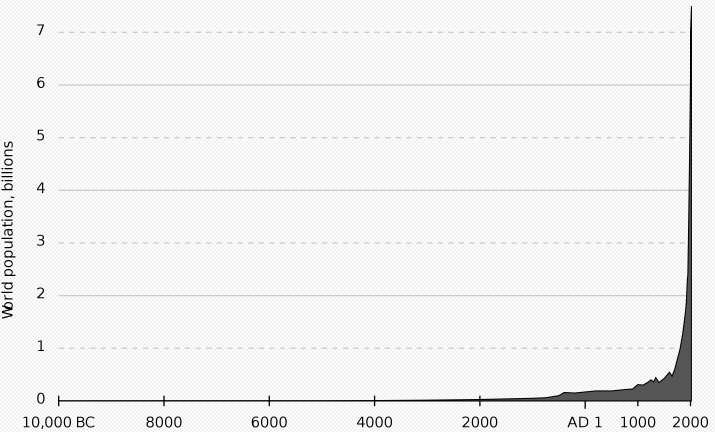
我们在阴影区域的任何地方随机投掷飞镖。 您是否注意到右侧有更多涂料？ 由于地球人口几乎呈指数增长，飞镖很可能会撞到图表的右侧。 因此，如果您生活，那么很可能您将生活在世界的尽头。 这称为“
世界末日争论” 。
自我指示假设
世界末日的论点很难辩驳-从逻辑上讲，这一说法是根据SSA公理学得出的。 因此，为了拯救世界，有必要改变这种公理学！ 与SSA相反，SIA主张：在
所有条件相同的情况下，观察者应考虑从所有可能的观察者集中随机选择他。SSA的根本区别是什么？ 由于Wiki文章相当含糊，因此我将尝试用自己的语言来表达，并且基本上表明SIA在有关睡美人和水手孩子的悖论中回答了1/3。 因此，使用SSA，您的灵魂将进入物理世界中的一个身体，并且它们的集合被认为是预先确定的（如果您站在永恒主义的立场上）。 相反，SIA被排斥：您的存在。 如果您以这种形式存在，那么很可能这是一个成功的配置，因此，可以合理预期会有许多这样的配置。 也就是说，您的化身谈到了这个世界上可能发生的事情。
我有一种感觉，SIA在多元宇宙中自动运行。 SIA与世界末日的争论大致如此：如果我们存在并且面前有那么多人，那么存在更多人的可能性就更大。 也就是说，您在一系列出生中的位置
n并不表示总共将出生多少人。 我建议阅读有关
SIA如何
与“世界末日”论抗争的文章，在这里，我将简单地写出文章中使用的词汇：
灵魂抱有实现的希望，生于这个宇宙，基于信仰，灵魂的储备，人类跨宇宙。
但是，有许多公式。 但是，让我们来谈谈直觉的含义。 您知道您的包位于一个不确定大小的暗室中（这个房间甚至可能长达一公里！），而且它被扔到了那里的随机位置。 你打开门...
...您会在门口一米处看到包。 您可以得出这样的结论：房间的长度不超过15-20米，并且极不可能达到一公里。 同意，这很合理吗？
绝佳筛选条件：世界末日反击
事实证明，如果我们回想起“
大过滤器” ，那么使用SIA可以摆脱困境。
可能处于多个阶段的路径上-生命的出现，多细胞生命的出现，心灵的出现，心灵的银河扩张等。 （总共9个阶段，请参见链接），其中至少一个阶段是极其困难的，为了实现这一困难阶段，生命通常会丧命或陷入僵局。 因此，过滤器可以是
较早的 （例如，生命的出现），也可以是
较晚的 （例如，由于机器人的银河膨胀或死亡）。显然，根据SIA，我们存在该过滤器为
晚期 ，这意味着
它已经存在即将推出 ：
通常，过滤器以一种非常有趣的方式工作。 想像一位公主。 为了赢得她的手和心，申请人必须在一小时内打开七个带密码锁的盒子。 在第一个框中，密码仅包含一个数字，平均密码猜测时间仅为十分之一分钟。 第二个框有两位数字，平均打开时间为1分钟。 第三-10分钟，100分钟，1000分钟，10,000分钟，最后100,000分钟（约70天）。 我提醒您，您必须有一个小时的时间来打开所有盒子，失败者将丧生。 但是，公主是如此的美丽，以至于那些想尝试运气的人并没有干:：
迟早，其中一名申请人会很幸运。 打开这七个盒子需要多长时间？ 明显地
但是什么时候会是特征性的？ 直觉说，前三个数字会像预期的那样小，但是对于复杂的任务，它将是
。 但是直觉欺骗了我们。 您应该预期大约以下时间：0.1、0.9、1、2、15、17、16、16-当然，数字可以变化，但是
非常简单的任务的执行时间将接近平均值，
平均复杂度的任务的时间将略微减少，但是
不切实际的复杂任务的执行时间将大致相同且相等
（60次简单和中等任务）/困难阶段数。
这种观察属于
尼克·博斯特罗姆 （
Nick Bostrom） ，我承认，直到我写了一个小型模拟器并追赶他，我才相信他的结论。
由此我们可以得出一个奇怪的结论-观察地球生命起源的历史，我们观察到了花费很长时间的多个阶段（例如，真核生物的出现，光合作用，多细胞生命的出现）。 这表明这些阶段很复杂，但是没有告诉我们这些阶段的相对复杂性。 但是，头脑的出现显然是一个简单的阶段-头脑是在许多物种中并行发展的，如果不是一个人，那就是10-20-50百万年，然后有人会发射火箭。
Bostrom的一些悖论
就
在这里 。 Bostrom正在认真考虑SSA和SIA。 但是，许多“极端情况”看起来很奇怪。 博斯特罗姆将这些案例称为亚当和夏娃的悖论，他们是第一批活着的人。 如您所记得，根据SSA的说法，灵魂可以进入任何身体，几乎令人难以置信的是，您将成为前两个生命的人之一。 尼克的话：
蛇理事会。 蛇爬到那对夫妇并发出嘶嘶声之后：“嘘……如果你们彼此相爱，那么夏娃要么生孩子，要么不生孩子。 如果她生了孩子，那么您将成为数十亿人口中的第一人。 但是成为出生链第一人的条件概率很小。 另一方面，如果夏娃没有怀孕，则只有两个人，成为两个人中前两个的可能性为100％。 根据贝斯定理，夏娃怀孕的风险不到十亿分之一！ 因此，彼此享受，不要考虑后果！”鹿的悖论。 由于亚当和夏娃没有在天堂里长大，他们有时间发明一种从试管中抚养一个孩子的方法，而且要有100％的保证。 但是亚当厌倦了每天打猎。 他用夏娃决定：如果今天没有受伤的鹿来，那么明天他们将生一个孩子。 现在，根据SSA的说法，亚当几乎可以完全确定，受伤的鹿很快就会亲自到达山洞中，他们只需要完成工作即可。奇怪的是，即使在我们这个时代，也有机会进行实验并检查SSA。
联合国++。 2100年，建立了一个无所不能的联合世界政府：联合国++。 任何UN ++解决方案都是完全可执行的。 但是，世界仍然无法抵抗外部威胁-例如，超新星爆炸可能会破坏整个世界。 此外，科学家发现附近的n颗恒星准备爆炸。 每次超新星爆炸产生的射线都可能以10％的概率极大地破坏地球（但不会完全破坏生命）。 但是，联合国++做出了这样的决定：对于清单上的每一种威胁，如果发生，联合国++都会在太空中建立殖民地，那里的人口数量将超过在地球上生活的人口的m倍。 如果m >> n，那么我们可以确定超新星爆炸不会影响地球。
玻尔兹曼脑
这个故事发生在很久以前，可以追溯到19世纪。 关于宇宙大爆炸和宇宙存在的有限时间一无所知，这带来了一个问题：如果宇宙一直存在（如当时所认为的那样），那么热死应该遭受很长一段时间，温度将不得不在各处平衡，生命将是不可能的。
玻尔兹曼（Boltzmann）看到了以下解决方案：如果宇宙是无限的并且有无限的时间，那么迟早会在其中产生任意大小的波动。 我们生活在这里。 但是，由于波动的可能性随着大小的增加而迅速减小，因此更有可能假设不存在像可见的宇宙那样大的气泡，而只有一个记忆着假设生活的人类大脑：
在下一秒钟，热气会吞噬这个大脑。 玻尔兹曼了解这一点
，因此自杀。 我们知道，没有任何问题像19世纪所想到的那样-宇宙已经从一个熵极低的国家发展了140亿年。 但是，玻尔兹曼大脑的想法并没有被忘记。 在哲学上，这种大脑被称为“
怪胎观察者 ”。 确实，举一个名为“
永恒的通货膨胀 ”的宇宙学模型为例：
让大多数气泡对“标准模型”的参数进行微调，使生命要么无法发展，要么几乎不可能（但
怪异的观察者是可能的）。 和我们一样，宇宙出现的可能性可以忽略不计。 但是，那时
怪异的观察者的数量将超过真实的
观察者的数量，我们宁愿有机会以玻尔兹曼大脑的形式体现出来，这是没有发生的。 因此，生命的可能性并不低。 但是，有了多元宇宙，我们正在进入一个完全陌生的领域。
在MWI中采样
在我的文章的
评论中展开了有关量子永生的有趣辩论。 但是我们可以在不了解采样如何在MWI中工作的情况下解决它吗？ 例如，在SIA中，我们所说的是“所有可能的观察者”。 但是，我们是否应仅根据分支规则计算分支数或考虑这些分支的“权重” /概率？ 我相信我们应该将其称为“ Born-Adjusted-SIA”或“ B-SIA”。 对于睡美人而言，如果硬币掉落的概率不是1/2，则B-SIA与SIA有所不同。
但是MWI的“分支”本身太小-例如，处理器的逻辑状态不取决于单个电子的状态（可能的分叉点除外）-否则它将太容易受到热噪声的影响。 因此，当我们谈论处理器的状态时，我们所谈论的是整个MWI分支的集合。 同样，大脑状态是MWI的单个分支还是逻辑上等效的一堆大脑状态？ （但这些分支将来可能会分歧）？ 意识与与这些分支相关的故事的不断分歧相关吗？
在无限宇宙中采样
如果您不相信MWI，那么这将无法挽救您。 相信无限的宇宙就足够了。 实际上，根据
贝肯施泰因的极限 ，物质可以在某个体积（球体）中驻留的状态数是
有限的，并且与该球体的面积（而不是其体积！）成比例。
由此得出两个有趣的结论：
如果您创建一个无限的宇宙，那么迟早会生成它的片段，那么您将最终获得独特的组合，就像从Lego收集世界一样。 因此，如果存在，则存在无限数量的副本。 如果这些副本处于相同状态，那么它们是否具有共同意识？ 我们不知道。 意识是一个难以理解的对象，我什至无法确定对它的平等操作。
其次，球体的面积与其体积（以及内部物质的质量）之比随球体半径的增加而减小。 也就是说，我们花的时间越多，它的安排就越简单（因为内部不可避免地存在关联和“混乱”）。 在无限大的范围内，物质的密度必须为零！ 但这不足为奇-如果
Max Tegmark是正确的 -应该如此-在数学宇宙论中，没有与初始条件有关的信息，这意味着多元宇宙的确定性发展保留了最初给出的零信息量。
如您所见，即使使用TOE，我们仍然有很多东西要学习，甚至没有涉及这些主题。 例如，我错过了
强自我抽样假设-Google吧！ 但是我们是否不必削弱某些科学原理，例如可证伪性原理？ 有可能
请参加民意调查
