祝大家好运!
考虑到空间多样性这一主题,我们已经谈到了通信信道中的衰落问题以及为什么会发生这种衰落。 今天,我建议更详细地讨论这个话题。
此外,在今天的文章中,我们将略微谈及 MIMO信道的空间相关性问题,这些问题在Haardt教授的移动通信( CSP )课程中通常进行了讨论 ,因此,我认为这样的出版物将不是多余的。 而且,我马上注意到,问题的范围不仅限于仅在移动通信中使用。
通常,我邀请所有对无线通信主题感兴趣的人阅读,然后开始吧!
柯林·史莱特“衰落的回忆” 是的,将所有内容简化为一个主题可能是矫kill过正,但是通过一些这样的隐喻,我想您可以想象接收器在对原始信息信号产生各种影响后会收到什么...
我们在说什么
让我们从这样一个事实开始:实际上,存在所谓的乘法噪声会影响接收信号的功率衰减 。
您可能已经猜到,这些术语并未直接用俄语和英语翻译,但这不是很重要。在英国文学中,“ 衰落 ”一词暗示着一定的影响力,事实上,它会导致我们的信号衰落而“衰落”。
在我们的文献中,通常使用衰落一词,这主要是由于多径效应:如果电磁波遇到由反射和衍射产生的副本,并且它们处于反相状态,则波将互相抵消-即通道确实冻结了 。
淡入淡出是快和慢 (淡入淡出)。
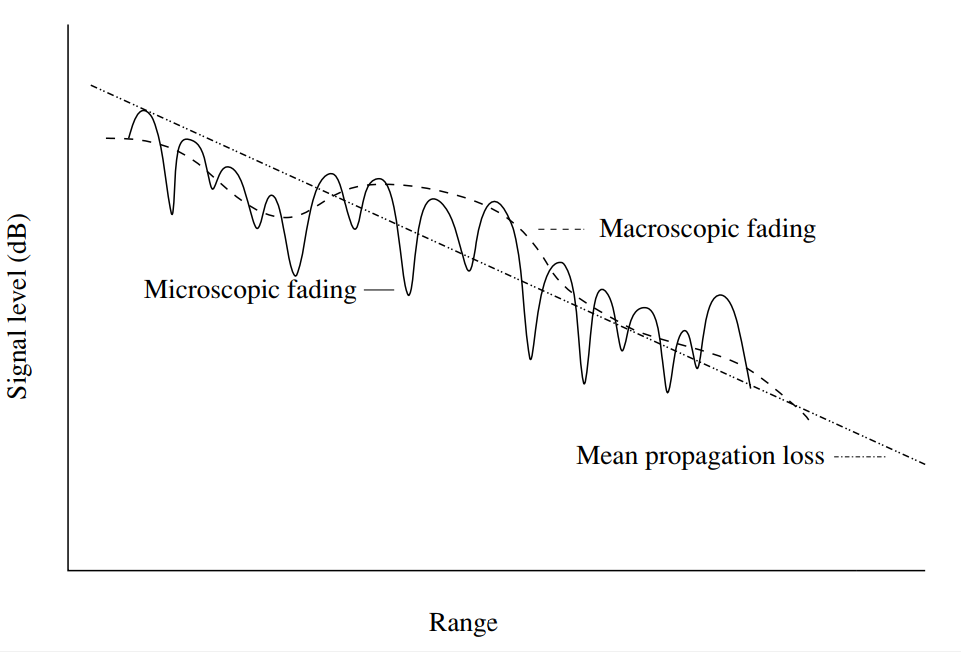
图 1.无线信道中信号功率的波动取决于距离。 传播损耗的平均水平随范围的增加而单调增加。 由于宏观(慢速)和微观(快速)衰落可能会发生局部偏差[1,p.14]。
我马上承认,今天我们不会使用慢衰落,但是我们将足够详细地讨论快速衰落。

图 2. 阴影效果的图示:通常,由于阴影而导致缓慢的褪色。 为了进行仿真,通常选择对数正态分布 。
如果您想阅读一些有关慢衰落的信息,特别是关于如何模拟卫星频道的信息,通常,我邀请您在这里 !
快速褪色
通常,发生快速衰落的原因有两个:
- 由于多径传播,我们已经提到和/或
- 由于多普勒频移 。
后者对于卫星系统非常引人注目,但由于地面通信通常情况下是固定的,因此对于地面通信并不总是考虑到后者。

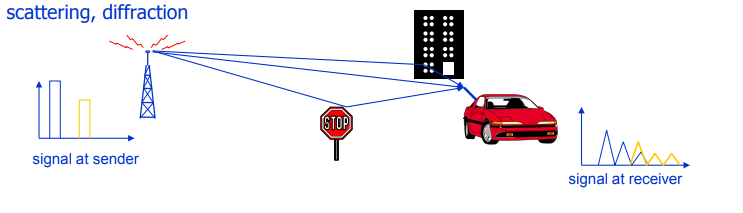
图 3. 说明褪色的原因。 要特别注意散射和衍射:正是由于这些现象,形成了所谓的多径传播,从而导致符号间干扰( ISI )。
但这远非全部。
选择性衰落与 平淡
上面,我们将干扰除以事件的性质 。 然而,干扰也可以通过对发射信号的影响的性质来划分。 在这里,我们需要通道选择性的概念。
我们根据[1,p。1]进行小分类。 14-18]。 因此,快速衰落可以是:
- 选择性的
一个 频率选择性
b。 时间选择
c。 空间选择性(这与EM波的到达和离开角度有关-今天我们将不再分析此问题) - 扁平-更倾向于慢衰落的性质(是的,这是一个悖论)
相反地解释了最后一个术语的含义。
首先,如果我们传输的信号的频谱宽度超过了信道的相干带宽 ,那么他们说我们正在处理频率选择性干扰。
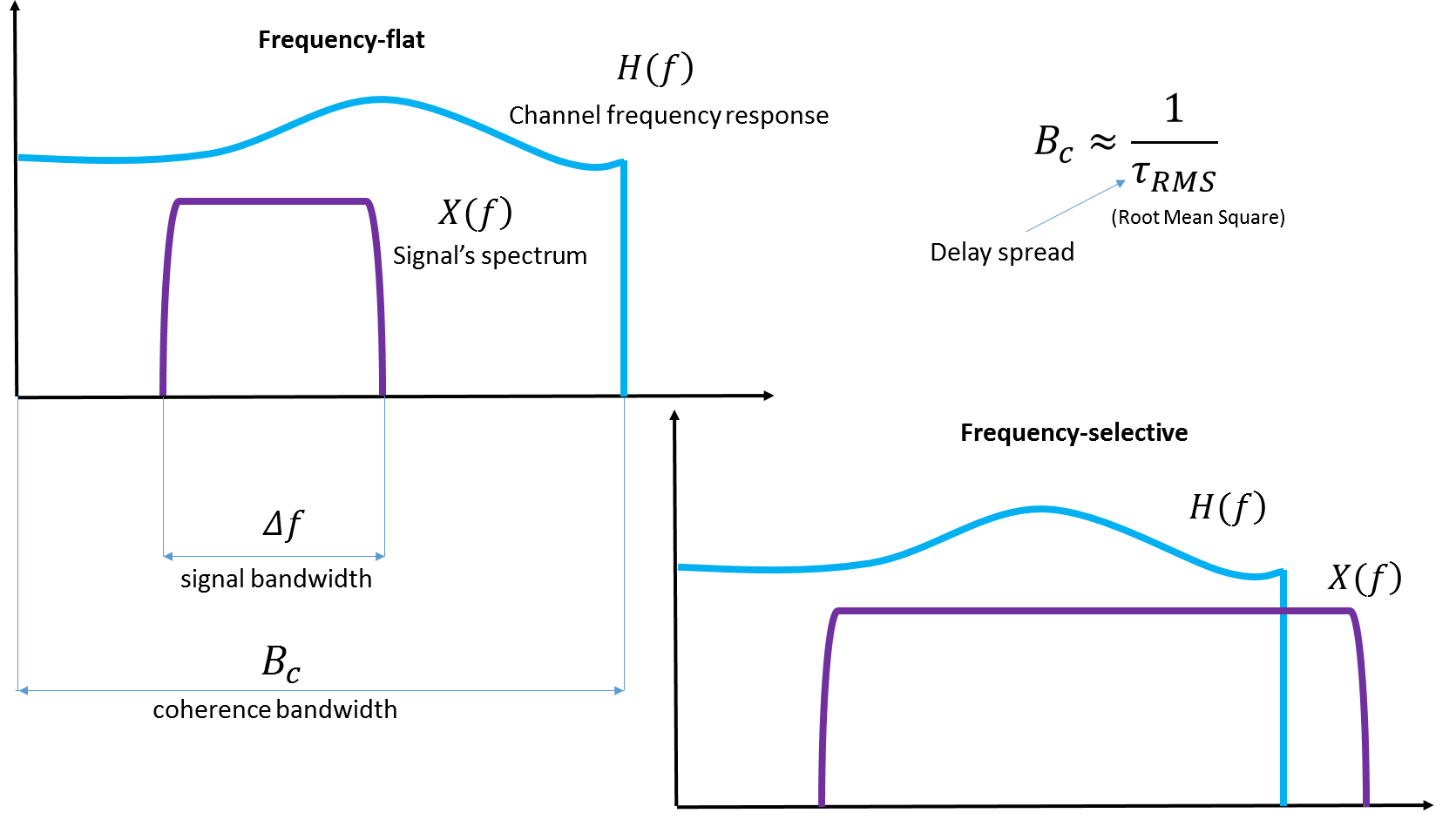
图 4.相干带宽的图示。 我认为,如果他自己在Wiki上添加插图,那么附上Wiki的插图将不是一个坏主意。
注意变量“ 延迟传播” - 延迟传播 。 当确定特定真实信道的特性时,就是在同一信号的不同副本的到达之间的延迟中的这种扩展。
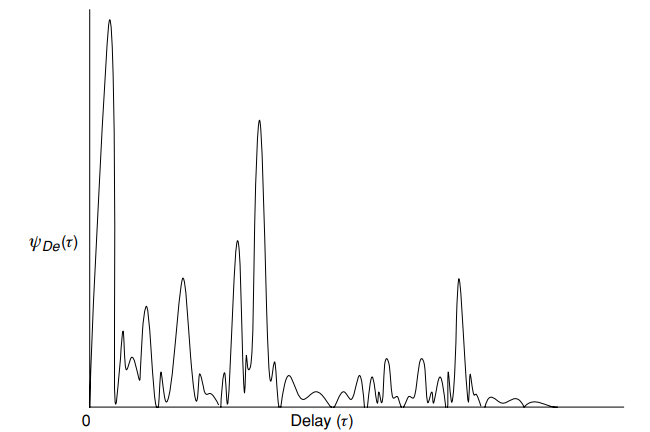
图 5.典型延迟(功率)曲线 ) -平均功率与延迟的关系
-平均功率与延迟的关系  [1,p。 16]
[1,p。 16]
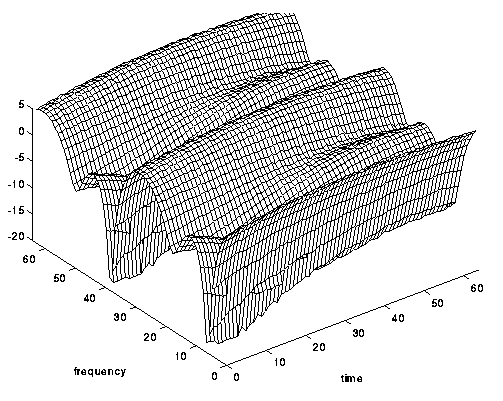
图 6. 频率选择频道,而不是时间选择频道 。
对于每个范围,相干频带都将不同。例如,对于S波段(当我在寻找有关卫星系统的信息时我很感兴趣)Bc = 0.5-2 MHz(Kanatas AG,Panagopoulos AD(编),《地球-空间系统的无线电波传播和信道建模》,CRC出版社,2016年) --第107页)。
这非常适合例如此类卫星收发器的波特率 。 毫不奇怪:数字调制的线性类型(PSK,QAM,OFDM)的符号率与信号所占用的频带重合(请参阅Goldsmith A. Wireless communications。-斯坦福大学,2004年。-第140、326页),这意味着尝试将信号最大程度地压缩到相干频带中会很不错。 频率仍然是宝贵的资源。
其次,如果我们在时域中的信号长度超过了信道相干时间 ,那么他们说我们正在处理随时间变化的信道。
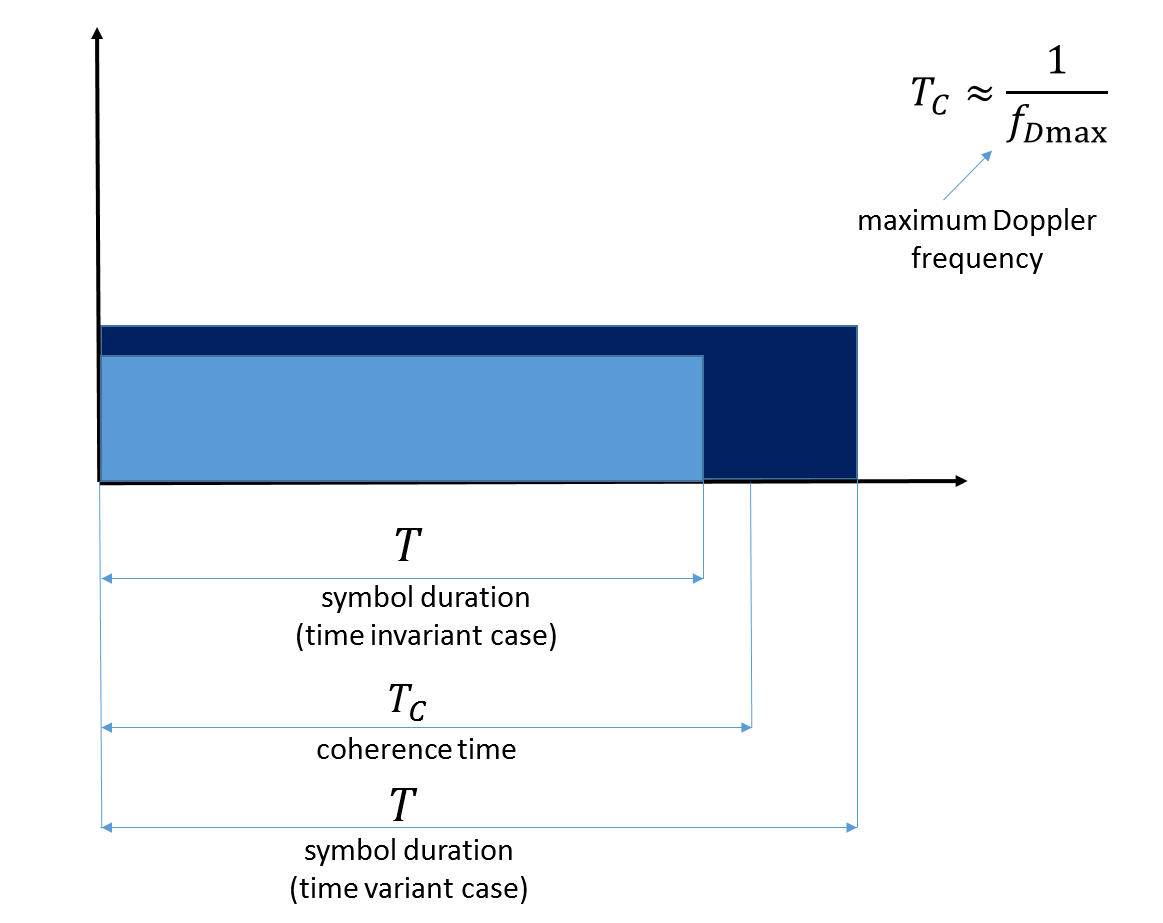
图 7.相干时间的图示。 请注意,此处最大多普勒频率反映了移动终端本身的移动。
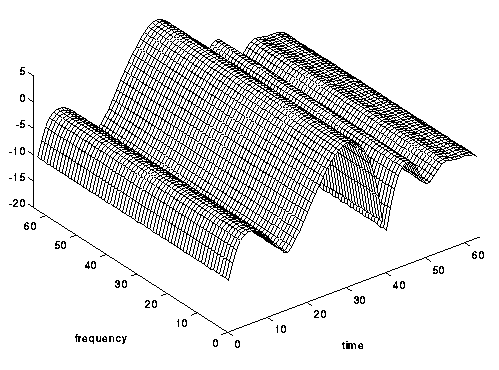
图 8. 几乎是时间不可见的,但是时间选择性的:快速衰减的通道。
好吧,因此,如果我们设法避免上述情况,那么我们将得出最简单,最方便的情况- 平坦衰落 [1,p。1。 [14-18]。 88-92]。
最简单的衰落通道
您可能已经看到了类似的方法来模拟在某处带有淡入淡出的平坦通道:
h = (1/sqrt(2))*(randn(size(msg)) + 1j*randn(size(msg)))
什么意思:
- 视线不足(有理由进行地面通信)
- 窄带信道(窄带信道)-适合相干频带
- 也没有频率选择性-适合相干时间
- 缺乏阴影和多普勒频移
就是说,它是亲自面对的 : 带有衰落的平坦通道 。 对于没有视线的情况,该通道也称为Rayleigh 。

雷利勋爵
这样的模型从何而来?
首先,谈到现代通信系统,我们很可能意味着处理数字信号。 此外,我们还最有可能使用正交类型的调制( I / Q ),即复杂信号。

图 9.信号星座图QPSK 。 极坐标,单位圆。 例如,符号 11 将对应于等于大约 0.7 + 0.7i 的坐标 。
假设干扰对实部和虚部都有影响,这是合乎逻辑的。 此外,值得遵循中心极限定理来假设这种效应的高斯性质。 我们写公式[1,p。 39]:
在哪里 ) 和
和 ) 是正态分布的随机变量。
是正态分布的随机变量。
大多数情况下,使用具有标准化平均功率的模型:
这意味着 ) 。
。
如果我们假设信号包络分量的独立失真:同相( I-同相)和正交( Q-正交),那么可以将原始符号乘以的数字位置(因此为乘性噪声)在极坐标系中为毕达哥拉斯定理从字面上计算得出:
在哪里 ) 和
和 ) -这些也是正态分布的随机变量。 额定功率
-这些也是正态分布的随机变量。 额定功率 ) ,
, ) 。
。
这就是瑞利过程的公式! [2,第78页]
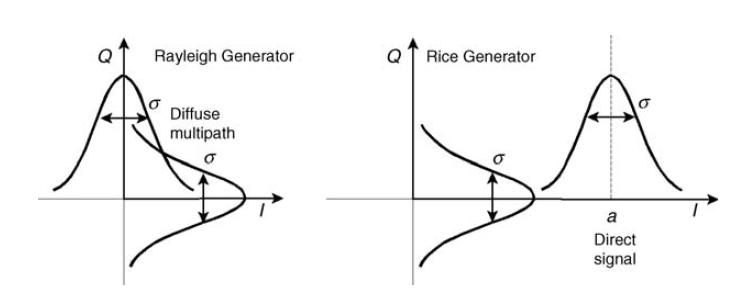
图 10.高斯平方发生器,用于建模瑞利和莱斯衰落[3,p.125]。 稍后我们将讨论莱斯频道。
抒情离题。就我个人而言,我真的很喜欢加农炮射击的示例:如果两把枪互相垂直射击足够多次,那么对于每个枪支,命中分布将是正常的,命中的总分布为瑞利。 我们的干扰正在发生类似的情况。
如果我们考虑最简单的情况,即信道之间没有任何空间相关性(假设我们有几个空间信道-MIMO ),那么他们会说信道是空间白色的-空间白色的 。 并且由于所有通道都是独立的,因此,不仅可以“生成”根据瑞利分布的随机变量,而且可以“生成”向量,矩阵和张量[3,p。125]:
在哪里 %20) 和
和 %20) 是由正态分布值组成的矩阵。
是由正态分布值组成的矩阵。
1/2是从哪里来的?这里的一切都非常简单:如上所述,信道响应功率应等于1,即:
为此引入了比例因子  。
。
演示(以python进行更改):
import numpy as np N = int(1e6) h = 1/np.sqrt(2)*(np.random.randn(N) + 1j*np.random.randn(N)) P = np.mean(h*np.conj(h)) print(np.round(P)) >>> (1+0j)
总结一下 :
根据具有圆对称和零垫的复杂高斯定律,在没有直接可见性的情况下,干扰分量可以描述为一个独立于n的矢量(取决于信道尺寸),独立地相同地分布( IID-独立地相同地分布)。 期望值( ZMCSCG-零均值圆对称复高斯)。
整个绕口令!
几乎是最简单的衰落通道
好吧,如果仍然可以直接看到该怎么办? 也许在这个分数上已经有现成的数学模型了?
当然有! 例如,对于具有多个接收和发射天线(MIMO)的情况,可以概括为[4] :
在哪里  -实际上,这是信道(或信道矩阵,如果我们谈论MIMO )的脉冲响应的复杂包络,
-实际上,这是信道(或信道矩阵,如果我们谈论MIMO )的脉冲响应的复杂包络,  是直接可见性(视线)的组成部分,并且
是直接可见性(视线)的组成部分,并且  -这是缺乏直接可见性(非视线)的一个原因,我们已经考虑过了。
-这是缺乏直接可见性(非视线)的一个原因,我们已经考虑过了。
注意变量K-这就是所谓的莱斯因子(Rician / Ricean因子) -直接传播路径的功率与所有其他路径的功率之比。 由他决定我们的频道将受到多少干扰。

史蒂芬·O·史蒂夫·赖斯
学期  表示信道矩阵的数学期望值,可以根据天线的接收和发射阵列的几何形状进行建模:
表示信道矩阵的数学期望值,可以根据天线的接收和发射阵列的几何形状进行建模:
在哪里 ) 和
和 ) -这些分别是天线的接收和发射阵列的响应,并且
-这些分别是天线的接收和发射阵列的响应,并且  和
和  是到达和离开的角度(离开的角度)。
是到达和离开的角度(离开的角度)。
这些因素通常是对称的,可以用以下通式描述:
在哪里  是波长之间天线之间的距离(天线间距),并且
是波长之间天线之间的距离(天线间距),并且  -这是天线阵列中的元素数量(图11)。
-这是天线阵列中的元素数量(图11)。
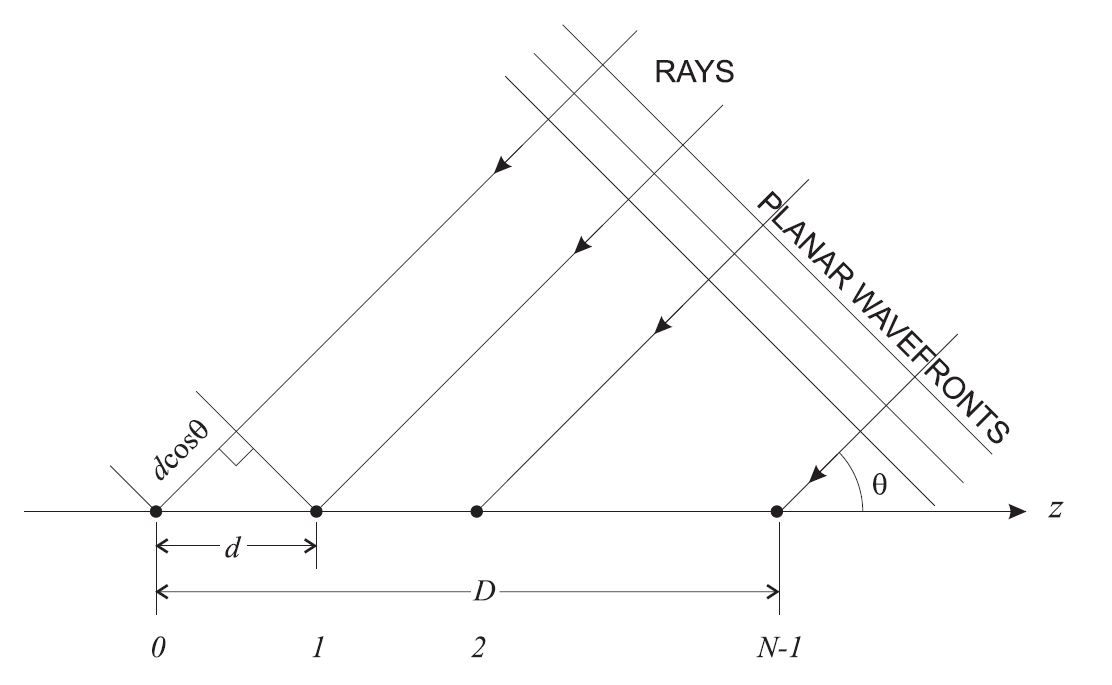
图 11. 线性阵列的几何形状 。 对于Massive MIMO,其几何形状当然会有所不同。 您可以在此处阅读有关此内容的更多信息。
好了,既然模型至少已经被分解了,您可以简化它。
对于SISO(最简单,最基础),公式(5)将采用以下形式:
用于1个发射和1个接收天线 %5Cmathbf%7Ba%7D_R(%5Ctheta_R)%20%3D%201) 。
。
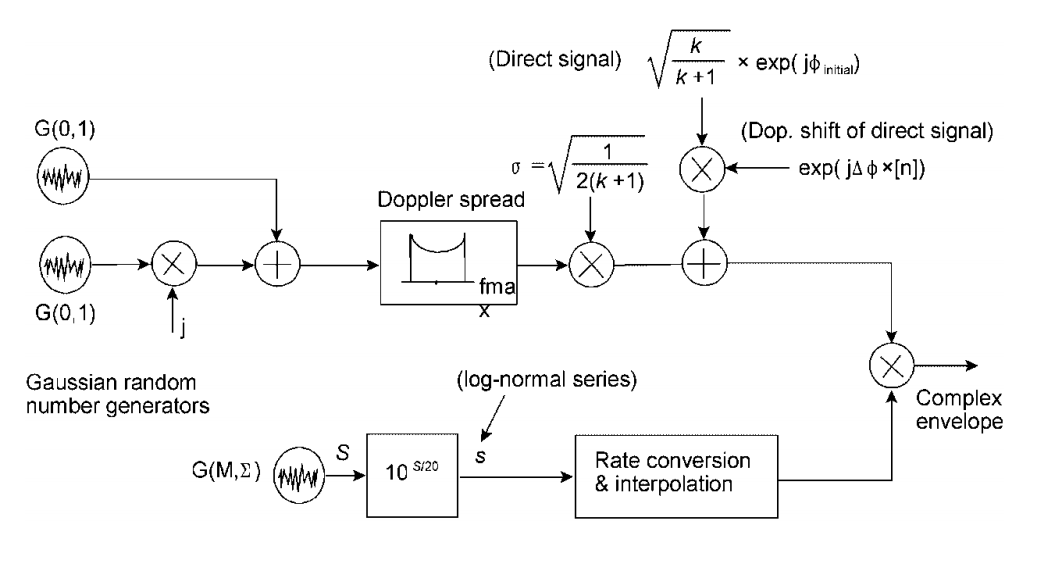
顺便说一下,这符合图12中的模型。
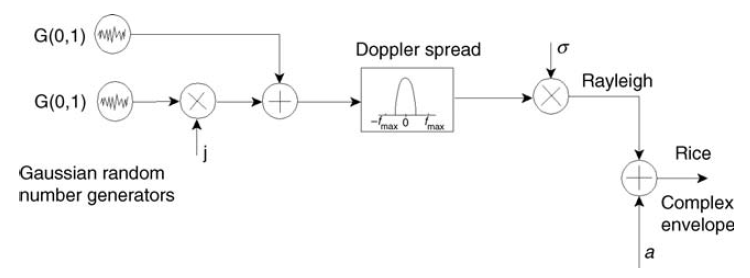
图 12. Rice信道的形成方案(窄带信号)[3,第127页]。 在  该频道将越来越多地退化为瑞利。 这就是为什么我几乎在副标题中使用该词:Rayleigh频道是Rice频道的特例。 从公式(5)也可以看出这一点。
该频道将越来越多地退化为瑞利。 这就是为什么我几乎在副标题中使用该词:Rayleigh频道是Rice频道的特例。 从公式(5)也可以看出这一点。
让我们解释一下: %7D%7D) 是Rician比例参数,并且
是Rician比例参数,并且  是非中心性参数。
是非中心性参数。
如果考虑平坦衰落,则假设多普勒扩展块的响应为1。通常,出于建模多普勒传播的目的,最有可能会遇到基于正弦和技术的Jakes模型(U形)。 从理论上讲,这种模型的频谱如下所示:

瑞利衰减的功率谱密度,最大多普勒频移为10 Hz。 来源
但是,在生活中,根据[1,p。 15]这样的频谱看起来仍然更少:
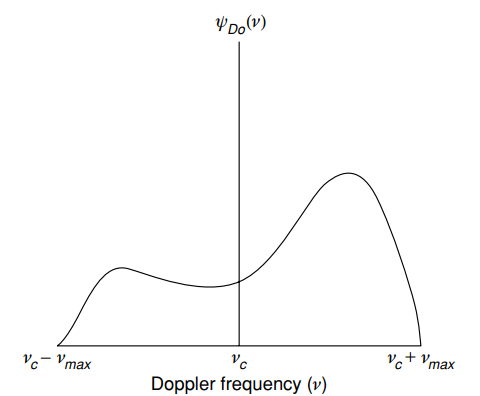
典型的多普勒(能量)谱 ) -平均功率与多普勒频率的关系
-平均功率与多普勒频率的关系 ) [1,p。 15]。
[1,p。 15]。
期望...现实。
有这样的方案可以与慢衰落结合。例如,这适用于Corazza-Vatalaro模型(C&V) :
参见Fontan,FP,Mayo,A.,Marote,D.,Prieto-Cerdeira,R.,Mariño,P.,Machado,F.&Riera,N.(2008)。 窄带陆地移动卫星传播信道生成模型综述。 国际卫星通信与网络杂志,26(4),291-316。
但这是一个完全不同的故事...
在MatLab中建模几乎最简单的衰落通道
让我们将接收到的计算与已经检查过的内容进行比较。 例如,使用特殊的MatLab函数 。
为了测试模型,就我们而言,我们生成了一个随机二进制消息(消息长度为100,000位),使用M-PSK或M-QAM对其进行调制,逐个元素地进行衰落过程相加,添加高斯白噪声,均衡零强制均衡器,进行解调和计算误码率(BER-误码率)(图13)。 测试数量将等于一百。
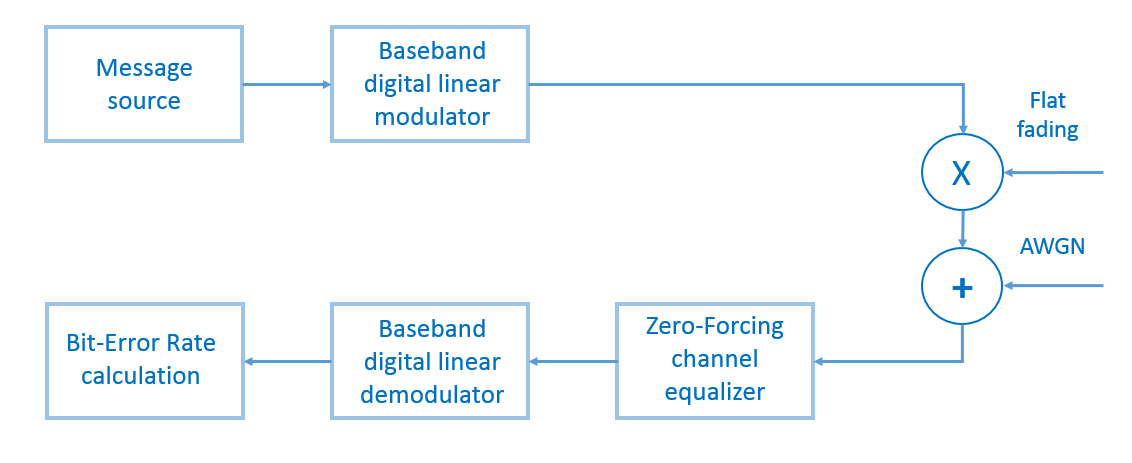
图13 我们的脚本将描述的传输系统模型的框图。
脚本可以在这里查看。在这里下载。
clear all; close all; clc EbNo = 0:40; K = [4.0; 0.6]; M = [4; 8; 16; 64; 256];
您应该得到这样的内容:
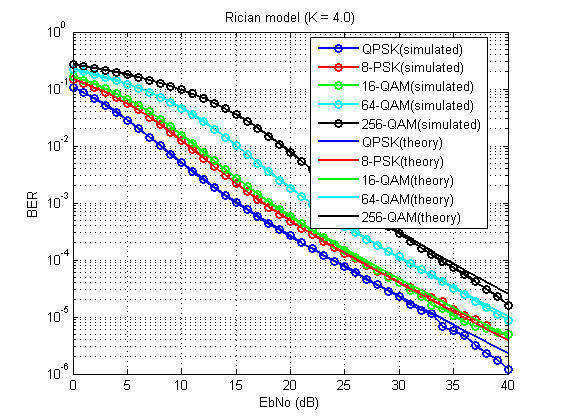
图 14.所考虑模型的误码系数(K = 4.0)。
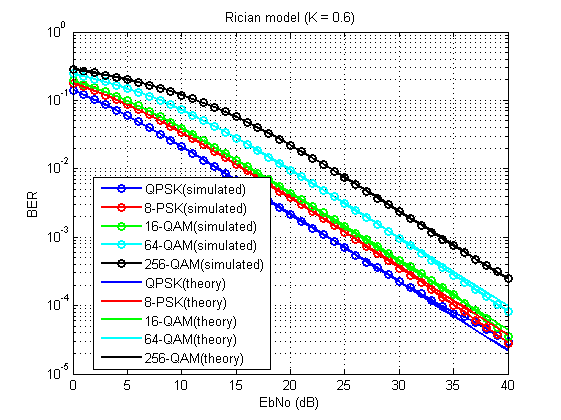
图 15.所考虑模型的误码率(K = 0.6)。
当然,并非没有缺陷(由于平均次数有限),但总的来说,可以看出它是可行的!
好的,但是可以将实验扩展到MIMO的情况吗? 当然可以为此,我们做一个假设:信道矩阵将由独立的传播路径组成,每个传播路径将根据Rice进行分配。
在什么条件下有可能?
如上所述,可以在任何维度上生成组件IID 。 这意味着可以将没有视线的任何空间白色MIMO信道建模为一组SISO信道(取决于信道尺寸)。
视线组件稍微复杂一些-您需要考虑光栅的位置。
考虑公式(5):如果我们的视线矩阵矩阵仅由单位组成  ,看来Raysov分量在空间上也会变白。
,看来Raysov分量在空间上也会变白。
为了解决这个问题,我们比公式(6)更详细地记录了视线组件:
)%20%20%5C%5C%0A.%20%5C%5C%0A.%20%5C%5C%0A.%5C%5C%0A%5Cexp(j(M_R-1)2%5Cpi%20dcos(%5Ctheta_R))%0A%5Cend%7Bbmatrix%7D%20%5Cbegin%7Bbmatrix%7D%20%0A1%20%26%20%5Cexp(j2%5Cpi%20dcos(%5Ctheta_T))%20%20%26%20.%20%26%20.%20%26%20.%20%26%0A%5Cexp(j(M_T-1)2%5Cpi%20dcos(%5Ctheta_T))%0A%5Cend%7Bbmatrix%7D%0A)
令人惊讶的是,如果  ,则矩阵将由一个单位组成。 从几何上讲,这是两个元素数组严格彼此定向的情况:
,则矩阵将由一个单位组成。 从几何上讲,这是两个元素数组严格彼此定向的情况:
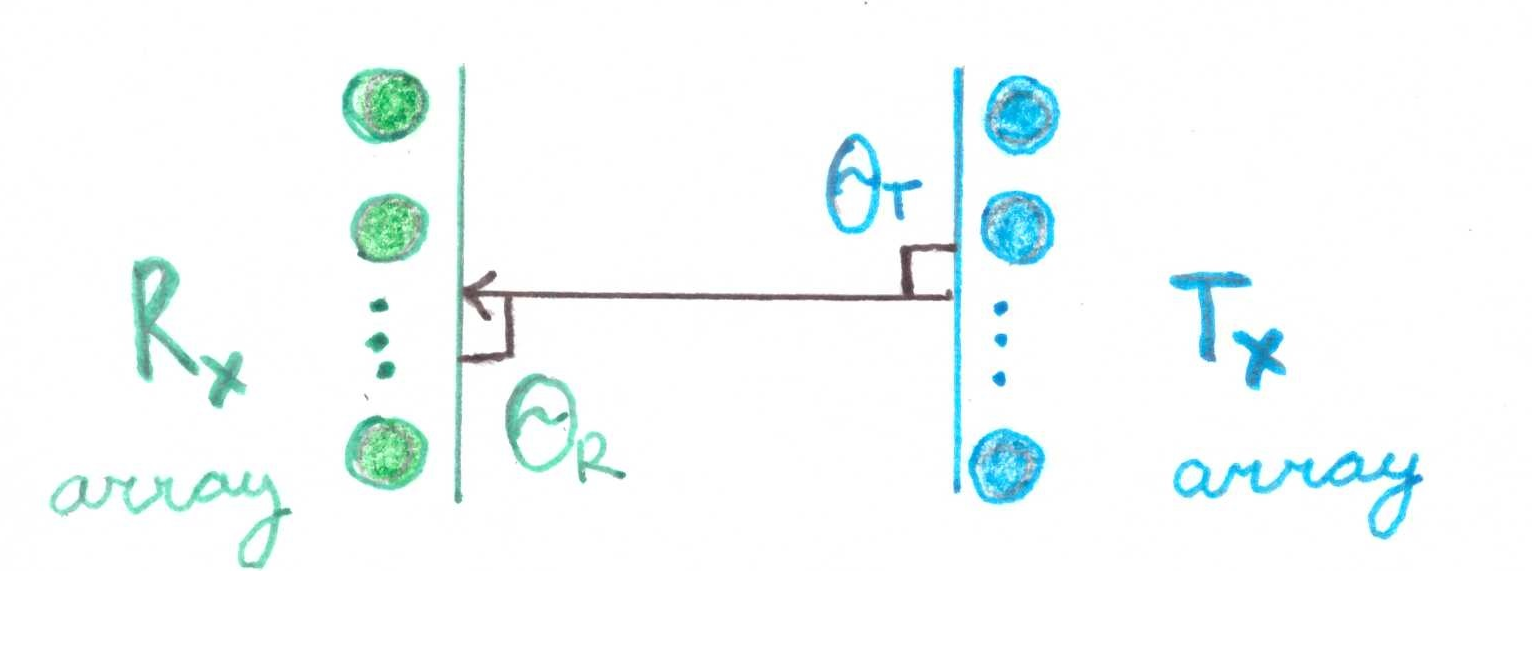
让我们做一些数学演示:
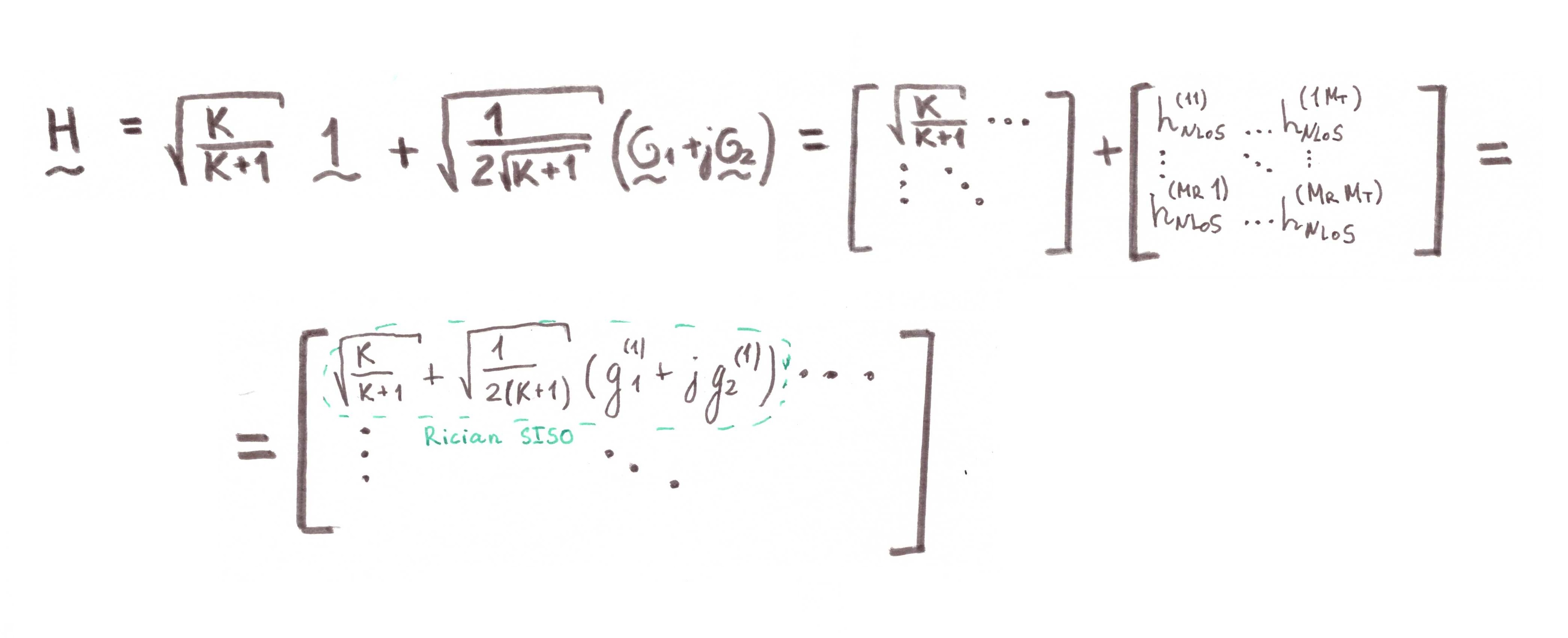
对于建模,我们以Alamouti方案为基础。 结果应该是这样的:
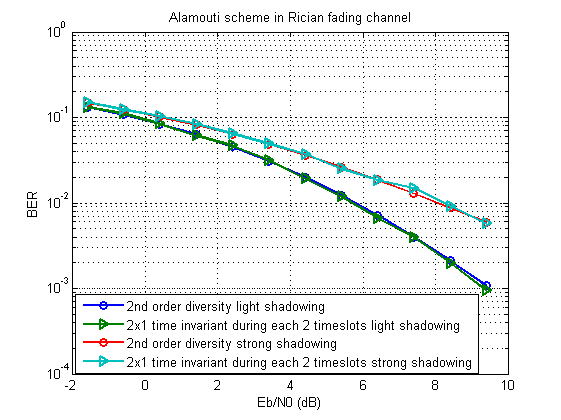
扩展脚本可以在这里下载。
干得好
几乎最简单的衰落信道和空间相关性
现在,完成我们进入统计计算世界的旅程,让我们更接近现实。
上面我们考虑了视线不足的部分在空间上是白色的情况 。 但是,从实际系统来看,人们仍然应该期望天线之间以及电磁波传播路径之间存在某种相关性。
我们引入一个新变量-空间相关矩阵:
其中, vec表示矢量化操作。 顺便说一下,这个矩阵只会影响视线不足的部分 ,因此在这种情况下  。
。
可以合理地假设,在现实生活中,首先通过测量确定此矩阵,然后才将其用于建模:
在哪里  是IID矩阵( w表示空间w )。
是IID矩阵( w表示空间w )。
注意,将矩阵提高到幂并不意味着提高每个元素的幂。 因此,在我们的情况下,不能在MatLab中使用sqrt()函数。 使用运算符^ 。
对于Python,不能使用常用的numpy模块的指数运算符**和sqrt方法。 您需要使用scipy模块的fractional_matrix_power方法。
如果接收器和发送器彼此足够独立,如图16所示,则可以应用Kronecker模型[1,p。2]。 40],以减少计算的系数数:
在哪里  表示Kronecker的作品 。
表示Kronecker的作品 。

利奥波德·克罗内克
我们分别考虑表达式矩阵的组成部分:
%5ET%5Cright%5C%7D) 是接收天线的相关矩阵,
是接收天线的相关矩阵,
 是发射天线的相关矩阵
是发射天线的相关矩阵
 和
和  -这分别是接收和发送天线的数量。 两种矩阵都是正半定Hermitian矩阵。 而且,矩阵的等级
-这分别是接收和发送天线的数量。 两种矩阵都是正半定Hermitian矩阵。 而且,矩阵的等级  受价值限制
受价值限制 %2C%20rank(%5Cmathbf%7BR%7D_R))) 。
。

图 16。
接收器和发射器不相关时的扩散器模型。 绿点表示扩散器,蓝色和红色表示接收器和发射器。 非常抱歉,这是TU Ilmenau作业之一的屏幕截图。
在这种情况下,信道矩阵可以写成:
但是,对于如图17所示的情况,您仍然必须使用完整的相关矩阵(请参见公式(9))。
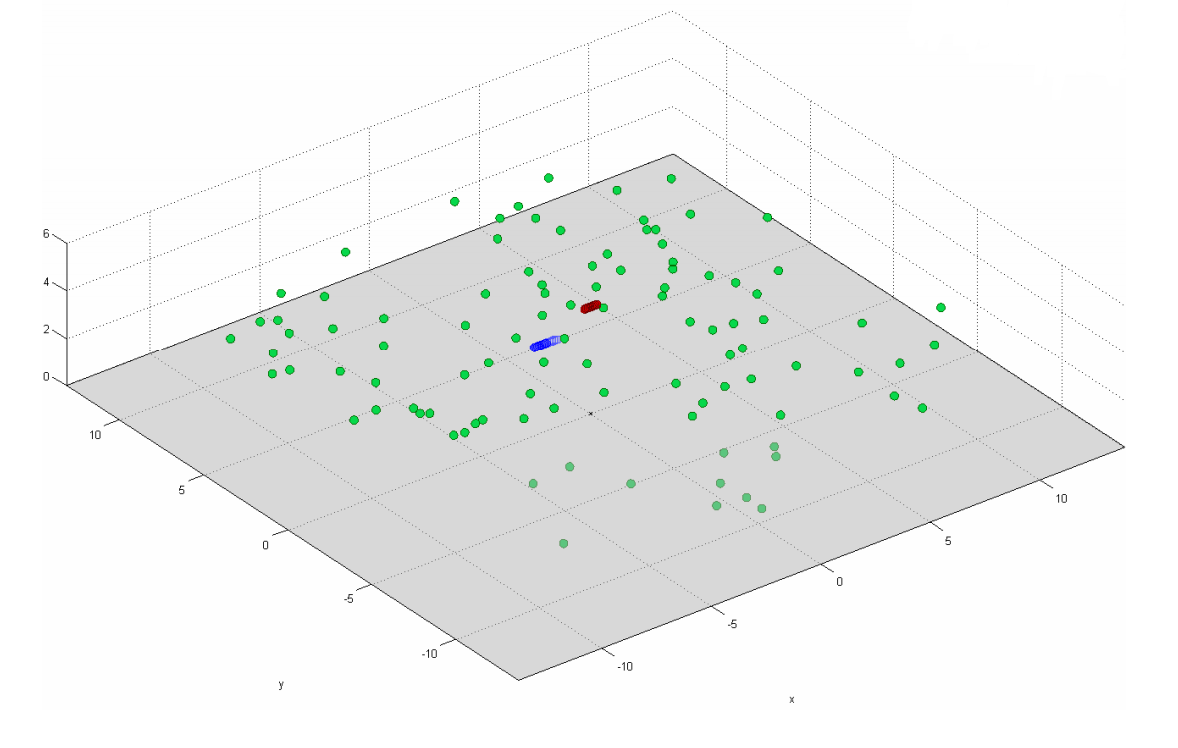
图 17.在使接收器和发射器相关的情况下的扩散器模型。 绿点表示扩散器,蓝色和红色表示接收器和发射器。
为了巩固我们所学到的知识,并了解空间相关性如何使生活变得复杂,让我们尝试计算通道的带宽 。 例如,对于MIMO 2x2。
为此,我们采用以下情况(我们都表示相同的平坦衰落,为简单起见,我们仅考虑瑞利信道):
1)空间白色通道;
2)具有相对弱相关性的Kronecker模型:
3)具有相对强相关性的Kronecker模型:
在这一部分中,我们将使用Python 3.4 。 计算带宽的函数将取自我以前的出版物之一 。
import numpy as np from numpy import linalg as LA import matplotlib.pyplot as plt from scipy.linalg import fractional_matrix_power def openloop_capacity(H_chan, SNR_dB): SNR = 10**(SNR_dB/10) Mt = np.shape(H_chan)[1] H_sq = np.dot(H_chan,np.matrix(H_chan, dtype=complex).H) lambdas = LA.eigvals(H_sq) lambdas = np.sort(lambdas)[::-1] c = 0 for eig in lambdas: c = c + np.log2(1 + SNR*eig/Mt) return np.real(c)
定义系统的主要参数:
Mr = 2
我们开始模拟:
counter = 1000 SNR_dBs = [i for i in range(1, 21)] C_MIMO_uncorr = np.empty((len(SNR_dBs), counter)) C_MIMO_kron1 = np.empty((len(SNR_dBs), counter)) C_MIMO_kron2 = np.empty((len(SNR_dBs), counter)) C_MIMO_kron3 = np.empty((len(SNR_dBs), counter)) C_MIMO_kron4 = np.empty((len(SNR_dBs), counter)) for c in range(counter): H_uncorr = (np.random.randn(Mr,Mt) + 1j*np.random.randn(Mr, Mt))/np.sqrt(2) H_kron1 = np.dot(Rr1_half, np.dot(H_uncorr, Rt1_half_H)) H_kron2 = np.dot(Rr2_half, np.dot(H_uncorr, Rt2_half_H)) for idx, SNR_dB in enumerate(SNR_dBs): C_MIMO_uncorr[idx, c] = openloop_capacity(H_uncorr, SNR_dB) C_MIMO_kron1[idx, c] = openloop_capacity(H_kron1, SNR_dB) C_MIMO_kron2[idx, c] = openloop_capacity(H_kron2, SNR_dB) C_MIMO_uncorr_erg = np.mean(C_MIMO_uncorr, axis=1) C_MIMO_kron1_erg = np.mean(C_MIMO_kron1, axis=1) C_MIMO_kron2_erg = np.mean(C_MIMO_kron2, axis=1)
画图 plt.figure(figsize=(7, 5), dpi=100) plt.plot(SNR_dBs, C_MIMO_uncorr_erg,'g-o', label='Uncorrelated') plt.plot(SNR_dBs, C_MIMO_kron1_erg, 'm-o', label='Kronecker model, case 1') plt.plot(SNR_dBs, C_MIMO_kron2_erg, 'r-o', label='Kronecker model, case 2') plt.title("Rayleigh flat fading (MIMO 2x2)") plt.xlabel('SNR (dB)') plt.ylabel('Ergodic capacity (bps/Hz)') plt.legend() plt.minorticks_on() plt.grid(which='major') plt.grid(which='minor', linestyle=':') plt.show()
我们得到:
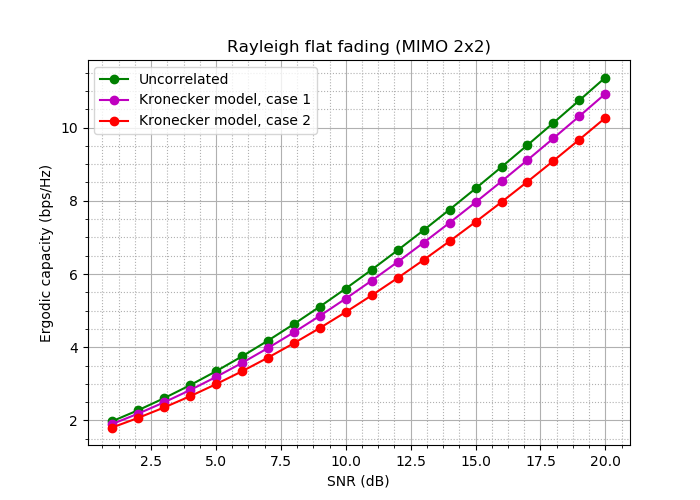
图 18.这些实验的带宽曲线。
好吧:虽然不是关键,但差异是!
后记
也许其中一位读者可能会注意到,我们今天检查的几乎所有内容(详细和附带介绍)都非常好地取决于matlab对象comm.MIMOChannel的参数。 在我看来,这一事实非常重要:
- 首先,它进一步将上述内容系统化,
- 其次,它强调我们正在解决当前问题。
好吧,现在,如果您使用这样的块,那么,我希望,这将更加清楚为什么以及您需要弯曲哪些笔。
谢谢大家的关注!
聚苯乙烯
我将在此处添加Reiner S.Thomä (伊尔默瑙)关于该主题的幻灯片的链接,他当时在该幻灯片上为我们做了演讲。 我认为有人会派上用场!
文学作品
- Paulraj,Arogyaswami,Rohit Nabar和Dhananjay Gore。 时空无线通信简介。 剑桥大学出版社,2003年。
- Goldsmith A.无线通信。 -剑桥大学出版社,2005年。
- Fontæn,FernandoPærez和PerfectoMariæoEspiæeira。 无线传播通道建模:Matlab的仿真方法。 卷 5. John Wiley&Sons,2008年。
- Farrokhi,Farrokh R.等人。 “带有发射和接收天线阵列的FDMA / TDMA无线系统的频谱效率。” IEEE无线通信事务1.4(2002):591-599。