分形的无理数。 第二部分

第0部分： 素数的分形。
第1部分： 无理数的分形。



本文包含Gif和对比图像。 癫痫病患者可能会癫痫发作。

在上一篇文章中，我们研究了二进制序列可视化算法。 让我们记住。

取二进制序列。 例如，上一篇文章中讨论的分形序列的前几位：

$$

$$Q_n = \ lfn \ sqrt {2} \ rfloor \; （\ textrm {mod} \; 2）; \ quad n = 0,1,2，...$$

0100110110010011001001101100

我们绘制一个方形单元场。 我们将位设置在上限。 位之间的距离是两个单元：



对于每一位，沿对角线（穿过单元）绘制一条虚线路径。 对于零，向右绘制第一个笔划：



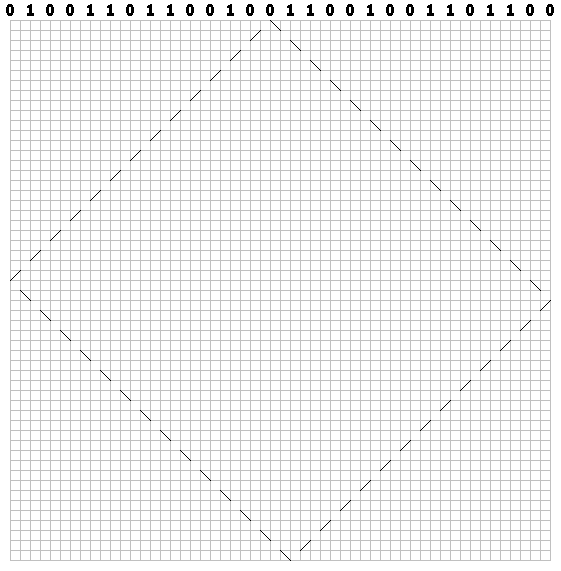
对于单位-左侧：



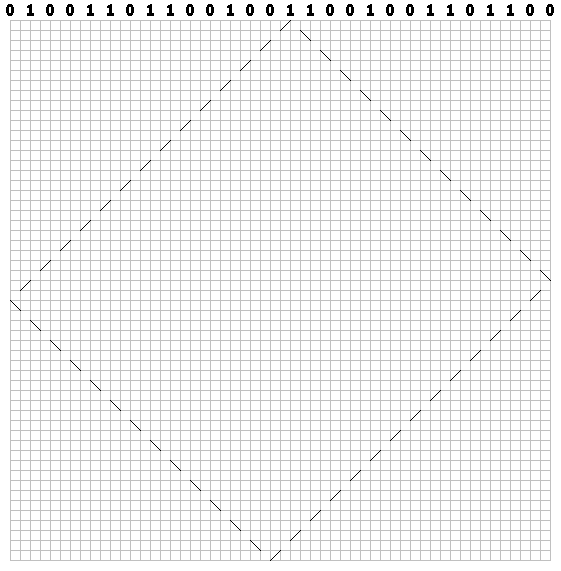
为每个位绘制一条轨迹。 我们有一个“台球”模式：



可以通过另一种方式获得相同的模式（沿对角线没有缺陷-序列是无限的，我们将其可视化为最终序列）。 反转序列中的每个偶数位：

0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 1 1 1 0 0 1 1 0 0 1

接下来，为每一位绘制垂直虚线：



我们将左侧的位设置为水平线：



我们结合：



写完第一篇文章后，两个问题仍未解决：

1.是否可以为无理数绘制分形图案。 可以的 在上一篇文章中解决了该问题。 在上图中-分形图案的一部分 $$$\ sqrt {2}$ 。 如果选择此模式中的一条曲线：



获得著名的分形曲线-“斐波那契单词分形”。

2.第二个问题是是否有可能编写一种绘制模式的算法：



本文将解决第二个问题。 我们将在织机的帮助下为图案着色，该织机的工作我们使用JavaScript进行模拟。



在上图中-最简单的机器。 它由两个框架组成，两个框架通过这些框架进行拉伸。 框架连接到踏板。 当您踩下其中一个踏板时，其中一个框架上升。 穿过该框架的螺纹上升，并且横向螺纹伸入螺纹之间形成的缝隙中。 如果通过不同的帧拉伸偶数和奇数线程，则将以棋盘格图案进行编织：



在更复杂的机器中，使用四个或更多框架：


Ashford 4轴桌织机

为了不混淆按下哪个踏板，他们绘制了一个图表。



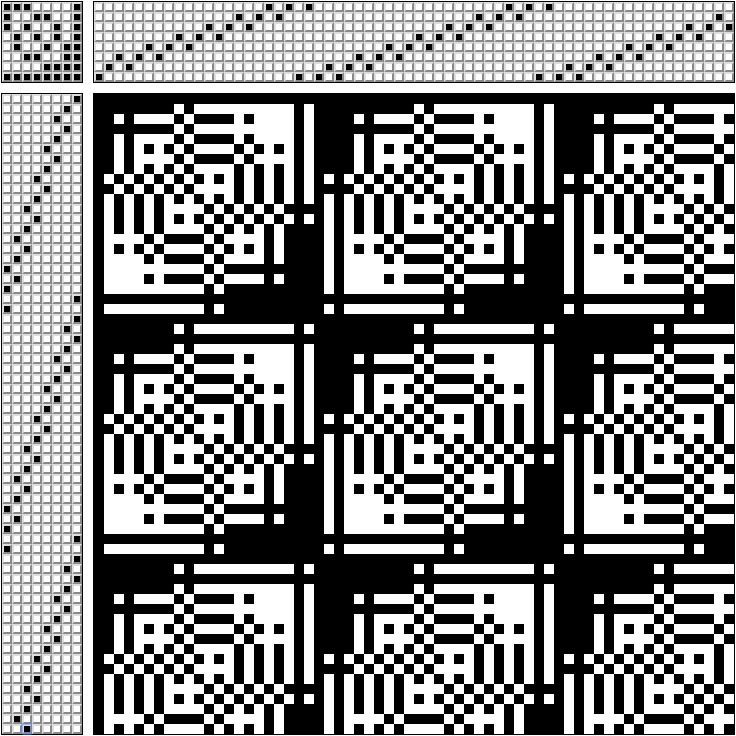
在花样的右上方，指示了螺纹穿过的帧（8帧织机的花样）。

在左上角-可以同时夹紧的踏板（每个踏板仅与自己的框架相连）。

在左下方-以什么顺序踩踏板。

在右下部分-我们得到了什么编织。 如果您将白色线穿过黑色线-我们会得到单色图案。

立即“输入”该原理似乎有点困难。 下图显示了编织图案的形成方式：



让我们编写一个脚本。 我们将使用一维数组array2将线程拉伸通过框架。 在一维数组array1中，我们编写了踏板夹紧的顺序。 在array3（8x8二进制数组）中，我们编写要同时夹紧的踏板。

for(var i=0;i<length;i++){ for(var j=0;j<length;j++){ if(array3[array1[i]][array2[j]]){ context.fillRect(i, j, 1, 1); } } } 

脚本 （适用于Google Chrome）。

在我们的简易织机的帮助下，我们可以绘制各种各样的图案：



但是从历史上看，普通人的腿只有不超过两条。 因此，方便的是同时夹紧不超过两个踏板。 织机最受欢迎的模式之一如下：



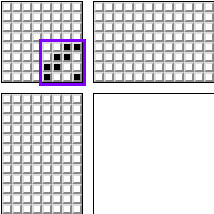
对于4帧。 及其针对8帧的修改：



出乎意料的是，使用此模板制作的图案（或图案的片段）类似于我们的“台球”图案。 另外，这些模式用阴影表示：



您可以学习为织机选择“台球”样式。 一个例子：



在本文的开头，我们已经看到了这种模式的一部分。

用织机完成并编写脚本以可视化二进制序列。 我们可以摆脱阵列之一-模式是对角线对称的。 如何填充剩余的数组？ 初级：



我们采用以下顺序 $$$\ sqrt {2}$ 。 创建一个数组。 在数组的零元素中，写入序列的零位。 交替取序列的每一位。 如果第n位= 1-将数组[n] = a [n-1] +1写入数组。 如果位= 0-写[n] = a [n-1] -1

$$

$$Q_n = \ lfn \ sqrt {x} \ rfloor \; （\ textrm {mod} \; 2）; \ quad n = 0,1,2，... \\ a_n = \开始{cases} a_ {n-1} +1，Q_n = 1; \\ a_ {n-1} -1，Q_n = 0 \ end {案例}$$

  var a=[0]; for(var i=1;i<size;i++){ if(Math.floor(i*Math.sqrt(2))%2==1) a[i]=a[i-1]+1; else a[i]=a[i-1]-1; } 

我们检查：

  for(var i=0;i<size;i++){ context.fillRect(i, a[i]+50, 1, 1); } 

实际上，我们已经收到了基本分形，但是我们将继续。

接下来，我们将处理矩阵：



总结一下 $$$x$ 和 $$$y$ 。 将模除以4。如果结果为0或1，则将矩阵写入true。 对于2和3，输入false。 我们可以不使用矩阵（事先不知道[n]取什么最大值和最小值）。 总结一个[x]和一个[y]。 在结果数量上加上一些数字 $$$C$ （以消除金额为负数的情况）。 将模除以4。对于值0和1，用坐标绘制像素 $$$x$ 和 $$$y$ 。

最终的算法只需要几行：

  var a=[0]; for(var i=1;i<size;i++){ if(Math.floor(i*Math.sqrt(2))%2==1) a[i]=a[i-1]+1; else a[i]=a[i-1]-1; } for(var x=0;x<size;x++){ for(var y=0;y<size;y++){ q=(a[x]+a[y]+512)%4; if(q==0 || q==1) context.fillRect(x, y, 1, 1); } } 

可视化我们的分形序列。

$$

$$Q_n = \ lfn \ sqrt {2} \ rfloor \; （\ textrm {mod} \; 2）; \ quad n = 0,1,2，...$$

您可以轻松地修改脚本以获得RGB图像：

  q=(a[x]+a[y]+512)%4; /*if(q==0 || q==1) context.fillRect(x, y, 1, 1);*/ if(q==0) context.fillStyle = 'rgb(255,0,0)'; if(q==1) context.fillStyle = 'rgb(0,255,0)'; if(q==2) context.fillStyle = 'rgb(0,0,255)'; if(q==3) context.fillStyle = 'rgb(0,0,0)'; context.fillRect(x, y, 1, 1); 

上面，我们在[x] + [y]的总和上加了一个数字 $$$C$ 。 如果不添加此数字，则总和的最小值= -8，最大值= 8（对于 $$$x$ 和 $$$y$ 从0到750）。 如果删除 $$$C$ -在某些情况下，总和为负且不是4的倍数，并且在这些情况下，像素没有被覆盖（保持黑色）：

  q=(a[x]+a[y])%4; if(q==0 || q==1) context.fillRect(x, y, 1, 1); 

您可以想象它好像分形的一部分在某个假想边界之下（在该边界之下，只有负值是4的倍数：-4，-8，-12，...）。

我们可以看到该边界在哪里：

  if(a[x]+a[y]>=0) context.fillRect(x, y, 1, 1); 

除了取模，我们可以将总和与某个特定值进行比较，从而仅在分形的一个“层”上进行绘制。 例如，取最小值和最大值之间的平均值：

  q=(a[x]+a[y]); if(q==0) context.fillRect(x, y, 1, 1); 

将值从最小值更改为最大值，我们可以看到动力学中的“层”如何变化：




另外，我们可以“在额头上”比较[x]和[y]并得到分形图案：

 if(a[x]==a[y]) context.fillRect(x, y, 1, 1); 

顺序如下：

$$

$$Q_n = \ lfloor n（\ sqrt {2} +1）\ rfloor \; （\ textrm {mod} \; 2）; \ quad n = 0,1,2，...$$

分形：



RGB：



中间层：



在动力学方面：

$$

$$Q_n = \ lfn \ sqrt {3} \ rfloor \; （\ textrm {mod} \; 2）; \ quad n = 0,1,2，...$$

分形：



RGB：



中间层：



在动力学方面：

$$

$$Q_n = \ lfn（\ sqrt {3} +1）\ rfloor \; （\ textrm {mod} \; 2）; \ quad n = 0,1,2，...$$

分形：



RGB：



中间层：



在动力学方面：

$$

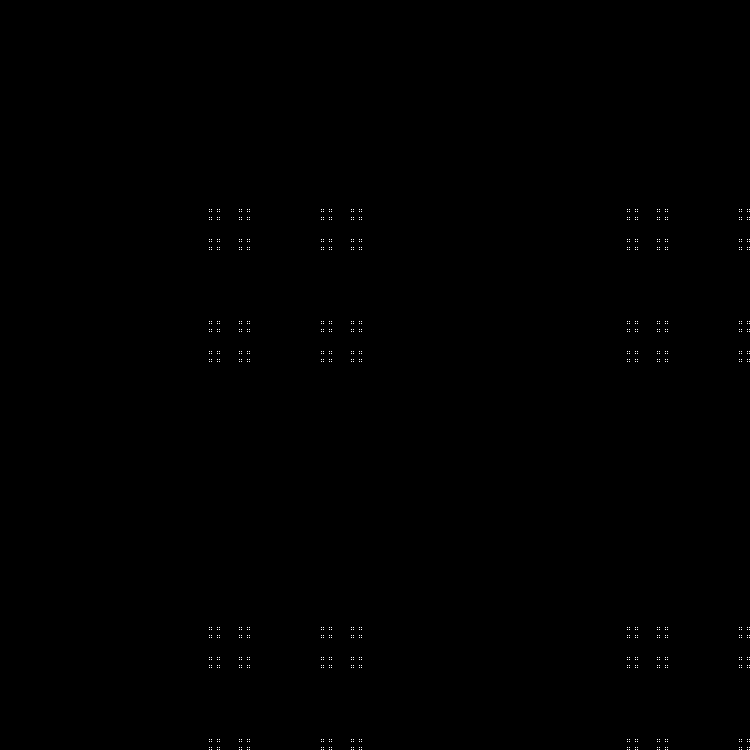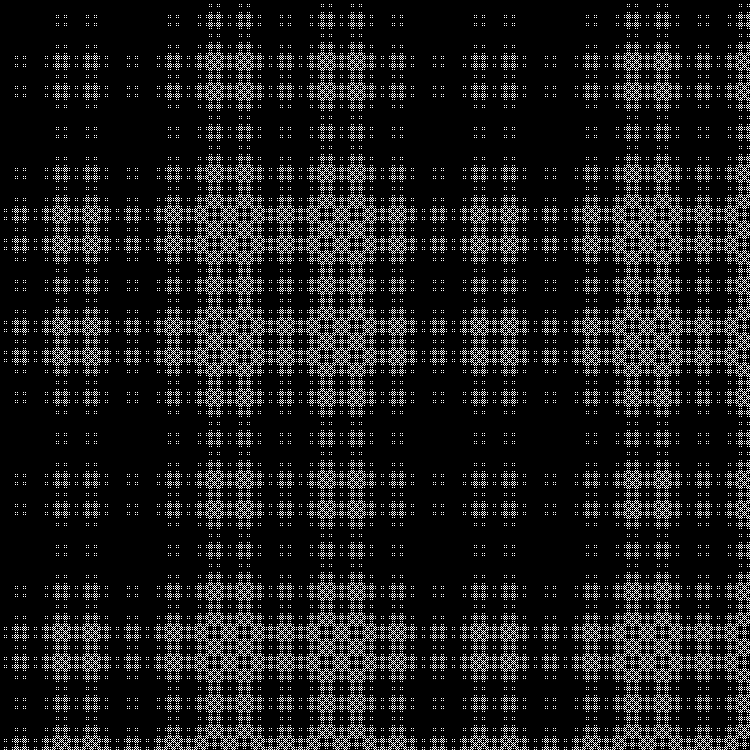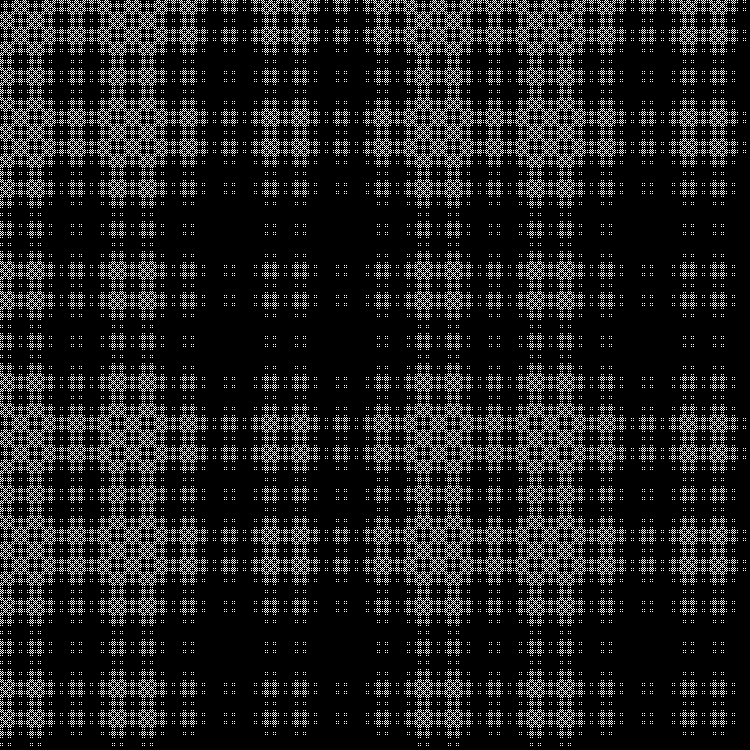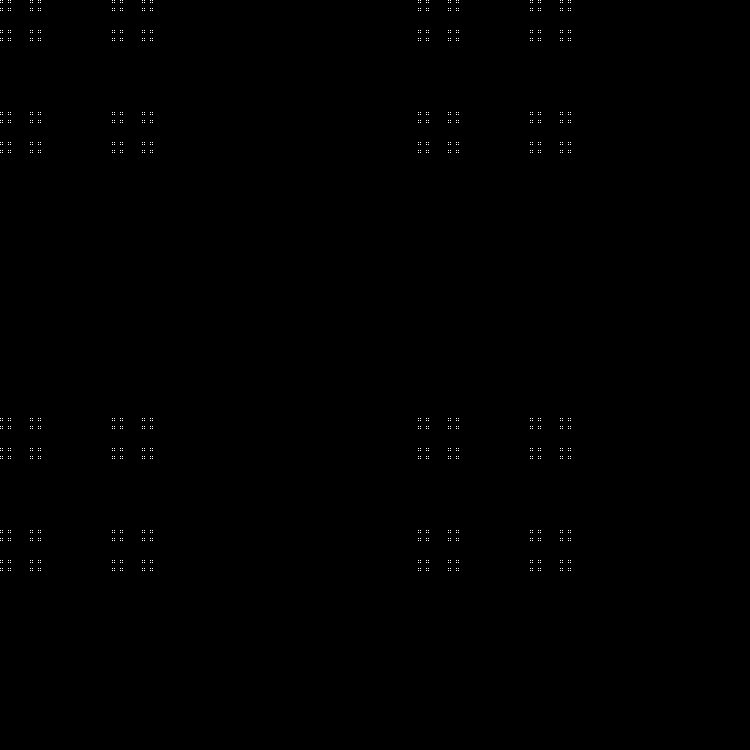
$$Q_n = \ lfn \ sqrt {5} \ rfloor \; （\ textrm {mod} \; 2）; \ quad n = 0,1,2，...$$

分形：



RGB：



中间层：



在动力学方面：



好吧，我们最喜欢的分形（此图案的一部分可以使用台球绘制，边尺寸等于斐波纳契数）：

$$

$$Q_n = \ lfloor n（\ sqrt {5} +1）\ rfloor \; （\ textrm {mod} \; 2）; \ quad n = 0,1,2，...$$

分形：



RGB：



中间层：



在动力学方面：



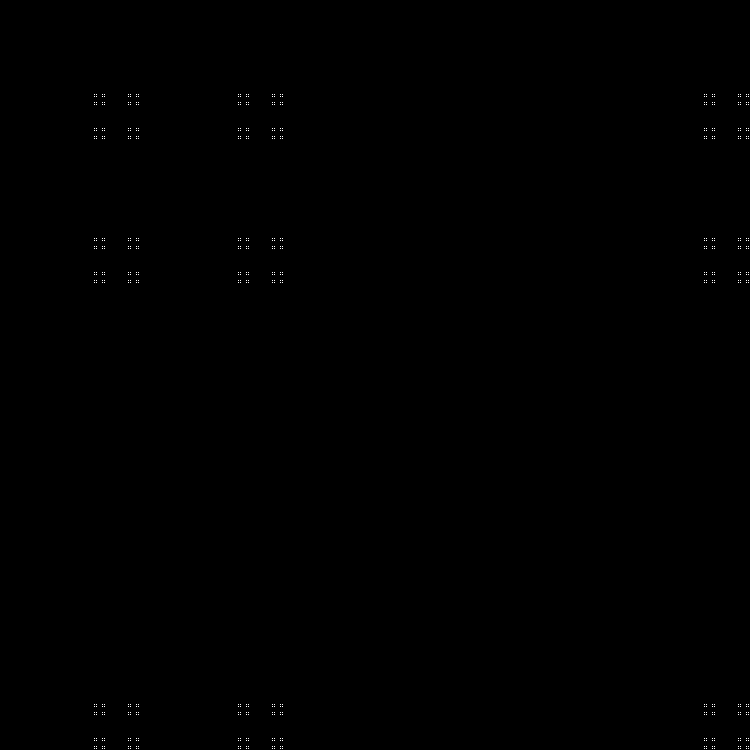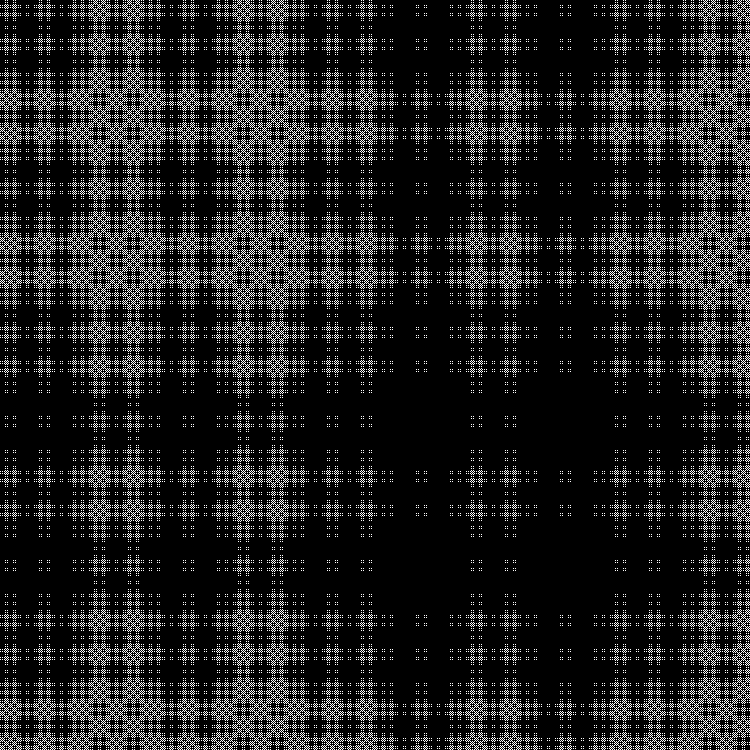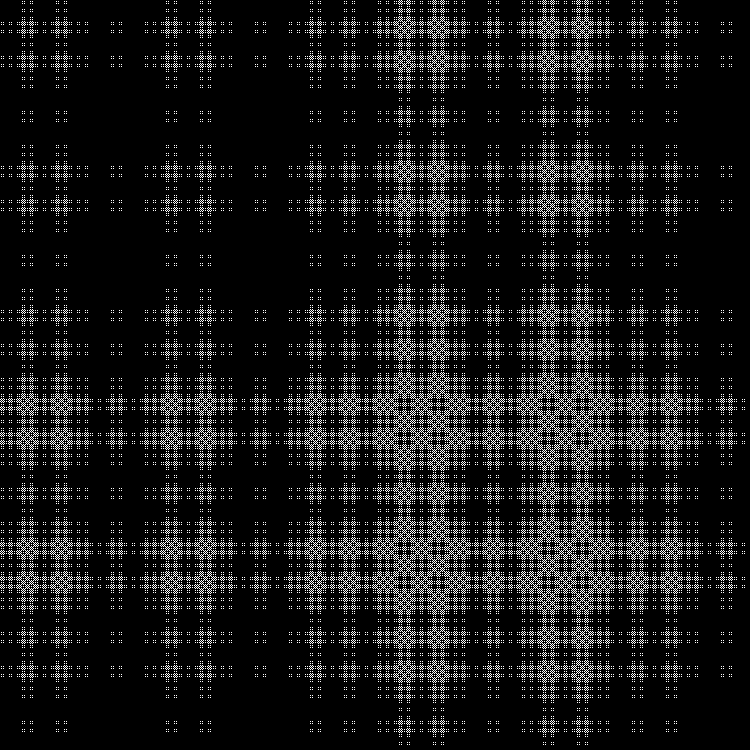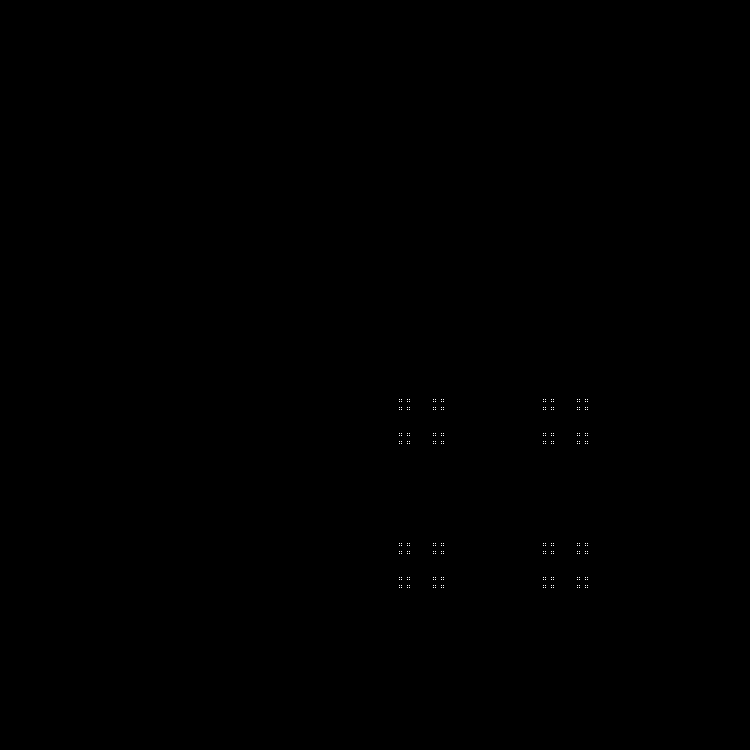
完成的另一序列：

$$

$$Q_n = \ lfn ^ {2} \ sqrt {2} \ rfloor \; （\ textrm {mod} \; 2）; \ quad n = 0,1,2，...$$

模式：



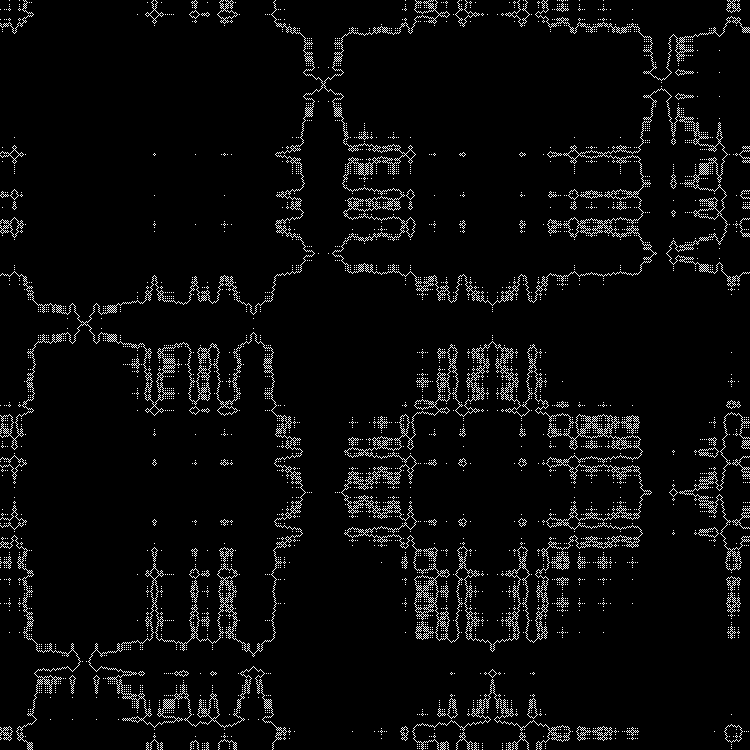
RGB：



中间层：



在动力学方面：



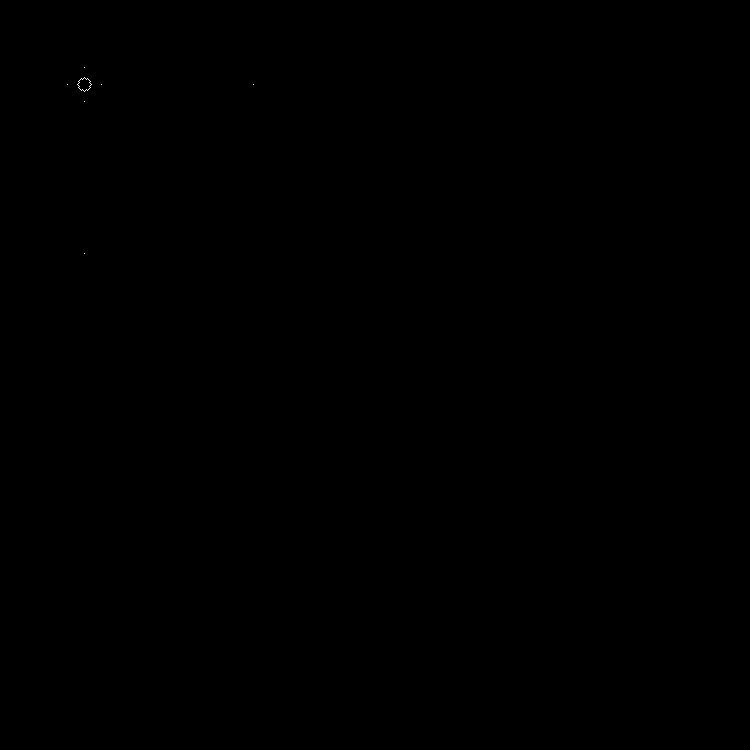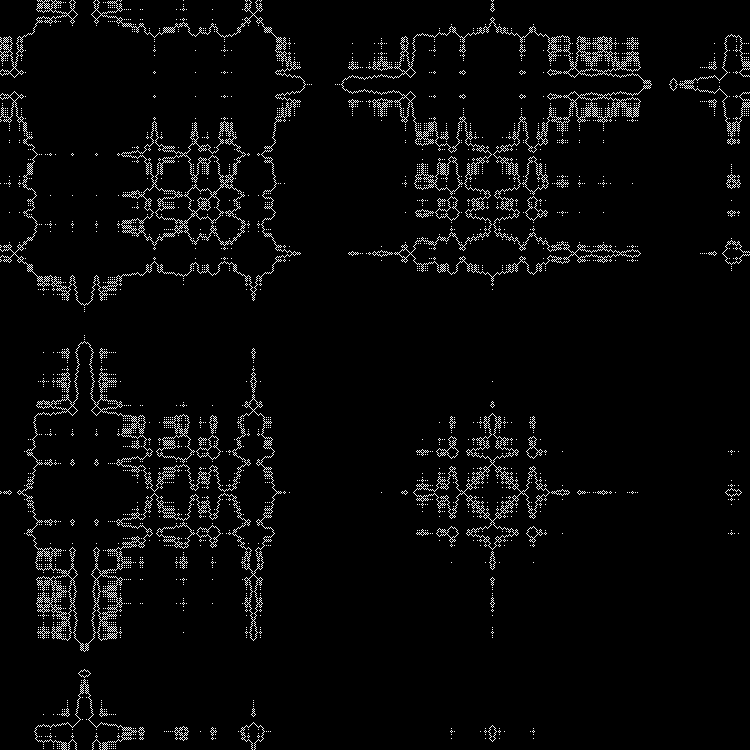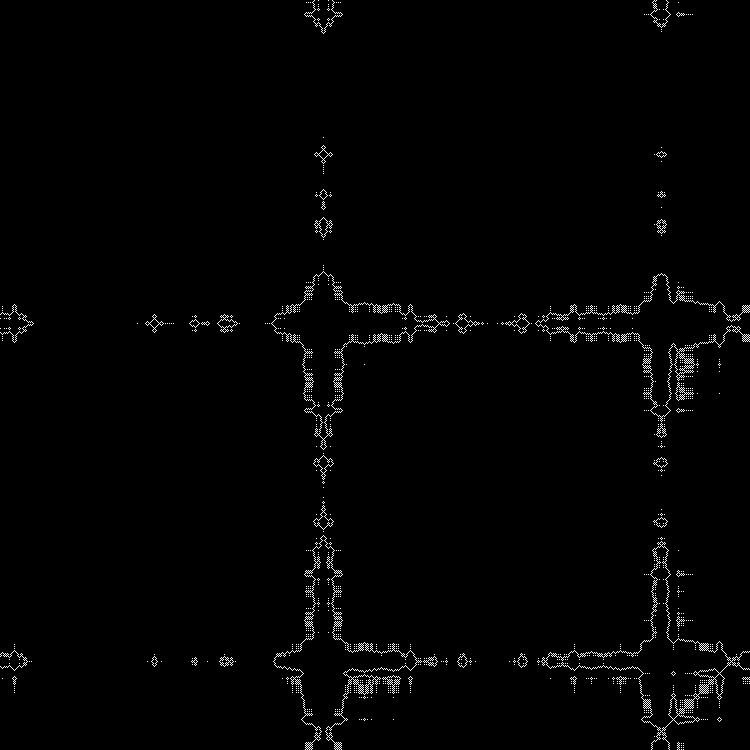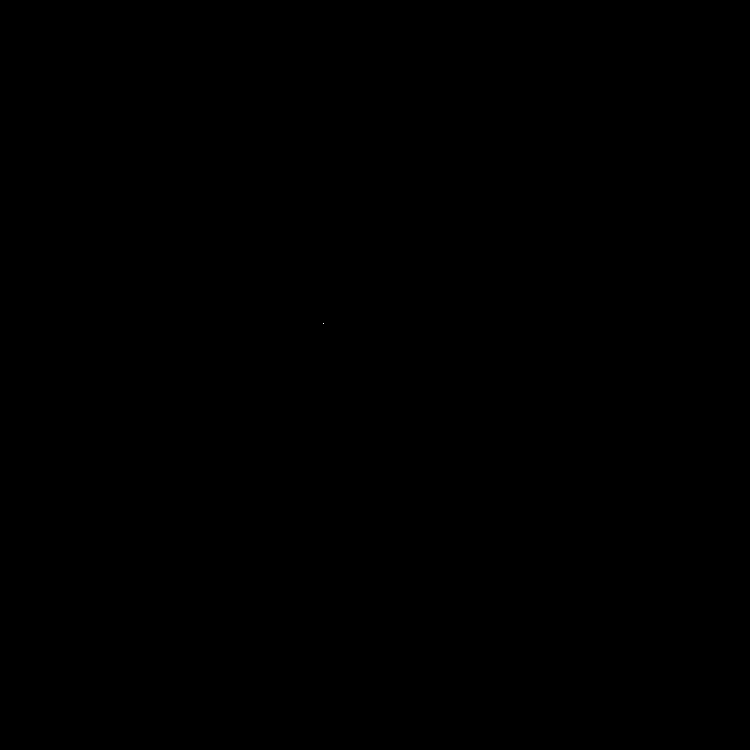
可以将其他平方根驱动到脚本中 。 （您可以驱动小数）。

在第二个脚本中，您可以手动驱动序列。

台球的另一个脚本 。 鼠标坐标-台球尺寸。 左侧的图案由使用除法的其余部分获得的序列形成（上一文章中的详细信息）。 在右侧-平价 $$$\ lfloor n \ frac {y} {x} \ rfloor$ 。