引言

关于项目

“绝对汇率”项目从事成对汇率的分析，对绝对汇率的分配及其分析。 在该项目的框架内，获得了一种从对汇率转换为绝对汇率的方法。 为此，定义了绝对货币ABS。 所有可用货币均以ABS表示。

在文章“从货币对到绝对汇率”中对该技术进行了详细说明。

关于问题

本文讨论了对汇率一致性进行定性分析的问题。
之所以需要研究货币之间的关系，是因为需要对投资组合中的金融工具进行选择，并具有基于与之相关的其他货币数据来预测货币行为的能力。

建议在投资组合中包含具有高多向连接性的工具。 这使您可以降低投资组合的总体风险。

而且，如果您发现具有高度连接性的工具，则可以根据某些工具的行为来预测其他工具的行为。

关于实验

方法选择

作为实验的初始数据，有一些具有绝对汇率的数据系列（请参阅源文件“绝对汇率”表 ）。



要研究一系列数值数据的连通性，最好使用Pearson相关（请参阅Correlation-Wikipedia ）。

相关系数具有从“ -1”到“ +1”的值的范围。 较大的负值表示强的多向关系。 大的正值表示较强的单向连接性。 系数接近“ 0”表示没有通信。

你想得到什么？

实验的目的是获得具有高度关联性的货币组。 此外，交流的信号也很有趣。

会场

所有计算将在Wolfram Mathematica系统中进行（请参阅Wolfram Mathematica-Wikipedia ）。 我们将使用Wolfram.Cloud免费云资源。

指定的资源允许您创建带有计算的在线笔记本，并允许您提供常规查看的访问权限。 该实验的笔记本位于此处 。

计划

我们将根据以下计划进行计算。

首先，我们计算相关矩阵。 矩阵的列和行将对应于各个货币。 列和行的交点将是对相关系数。

接下来，我们选择联系最紧密的货币对。 将选定的对放置在图上（请参阅图（数学）-Wikipedia ）。

图的节点是货币。 图表的边缘将指示货币之间的关系。 肋骨的颜色将指示键的符号。 绿色表示正向关系，红色表示负向关系。

所指示的计算顺序将针对绝对路线及其更改执行。 通过分析绝对课程之间的关系，您可以探索缓慢的过程（超过一天）。 对绝对汇率变化之间的关系进行的分析将使我们能够研究货币之间（一天）的快速联系。

结果

采样深度

源文件包含最近150天的数据。 根据他们的意见，将进行计算。

货币云

实验涉及45种货币。



货币的完整列表可以在源文件的“货币摘要”表上看到 。

绝对速率相关

上面（请参阅计划），已计划计算绝对利率的相关矩阵。 结果如下图所示。



在此，红色对应于正极，蓝色对应于负极。 为了理解，给出了等级量表。 左下方和左上方是货币行情（简称）。

绝对速率依赖图

相关矩阵可以区分高度关联的两组货币。 为此，选择相关性高于0.9的对并将其转移到图形中。



第一组收集了高度依赖美元的货币。 以下是四个以石油，港元和美元本身交易的阿拉伯国家的货币。 所有依赖关系均为正（单向）。

第二组收集欧洲货币。 欧元本身位于中心，周围是波兰，罗马尼亚和丹麦的货币。 所有依赖关系均为正（单向）。

绝对利率的相对变化

为了进一步研究，我们计算了绝对比率的一系列相对变化。 计算公式如下。



连续值之间的差异将与两者中的较早者相关。 因此，我们将获得绝对速率的相对变化。

绝对利率的相对变化的相关性

对于绝对课程，我们获得一个相关矩阵，用于绝对课程的相对测量。 我们给出矩阵的图形显示。



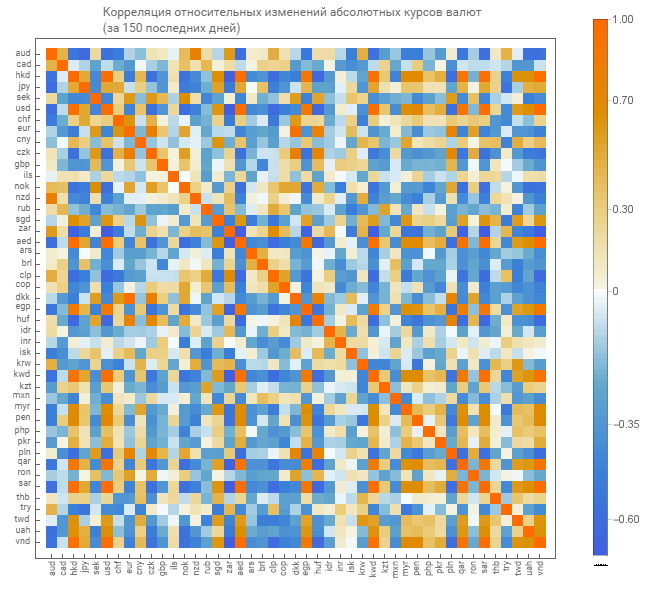
已经有一个较浅色调的矩阵。 这表明联系程度较低。

绝对利率相对变化的依赖性图

从相对变化的相关矩阵中，我们选择具有高度关联性的货币对。 这里只有采样水平已经是0.6（在此及以上，该系数是从考虑少数对的选择中选择出来的，以输出到图形）。



在相对变化的情况下，收到了3组货币。 上层人群将澳大利亚和新西兰的货币合并在一起。 较低的一组收集欧洲货币。 港元周围的中间国家组合了美国，越南，五个阿拉伯国家（石油出口国，南非和秘鲁）的货币。

此外，对南非兰特的高度负面依赖也有一个有趣的特征。

结论

作为实验的结果，我们设法获得了以下内容。

将相关矩阵数据放入数学图中是相关矩阵的一种很好的可视化实践。 进一步应用此方法将简化对数字序列组中关系的理解。

找到了一种聚类货币市场的正式方法。 可以正式区分欧洲，美洲，亚洲和大洋洲的市场。 这种方法可以大大缩短揭示不同国家市场之间相互影响的路径，并成为财务分析师的好工具。

将南非兰特与美元一起计入投资组合将减少此类组合的风险。

文章目录