给定: 12个硬币,其中之一是假的,只是重量不同。 未知更轻或更重。 给出的杠杆比例显示一侧的负载较重。 对于3称重,您需要找到一枚假硬币。
根据经验,我建议您不要着急,以书面形式做出决定。 我一生中几次出现“ 12个硬币,3个砝码”的谜题。 我的朋友第一次问我,她决定在奥运会结束后决定,我不得不摔了几个小时。 几年后,它没有立即交给我。 如果您想自己决定-在一张纸上做。
以下是解决方案的分析和阶段。 这些阶段将根据解决问题的通用方法进行,该方法既适用于编程,也适用于生活。 通过这种方法,解决难题将变得容易。
我建议您在阅读之前提供解决方案。 你有答案吗? 已验证?
如果是软件,那么问题将是:“您是否已编程,测试了算法? 您检查过测试用例并检查了吗?”
如经验所示,要解决该问题,需要绘制决策树并检查所有12种情况。

1.提示在解决过程中将有帮助:1)熵的减少(不确定性的度量)并回答以下问题:
- 您在上一步中学到了什么?
- 什么减少不确定性?
- 我们有什么信息?
- 您还需要知道什么?
问题适合于任何任务,项目。 对他们的回答有助于减少未按时完成任务,预算超支和赶上级的风险。
2)分解。 从简单到复杂的方法。 如果您准备了最简单的情况的解决方案,然后使用它们来解决问题(分而治之,算法),那将比在脑海中展现整个情况要容易得多。
分而治之算法将一个任务分解为两个或更多个相同类型的子任务,但比基本任务小,并结合其解决方案以获得原始问题的答案。撰写分解问题。 您会建议哪个?
2.分解您为分解提出了哪些问题? 有比赛吗?
1)最基本的情况是什么? 我们一次称重能做什么?
对于一次称重,我们可以确定哪种硬币重,硬币的重量是否相等。
2)如果我们有2枚硬币,并且您知道,假币变得更难或更轻。 如何在一次称重中确定假货?
有必要称量硬币,并根据天平的箭头确定假货。
3)如果我们有2个硬币,而假币变得更难或更容易(未知),那么如何在一个称重中确定假币呢?
在称重2个呈现的硬币之一和第三个硬币之后,已知它是真实的。
4)如果我们有3枚硬币,并且您知道,假币变得更难或更轻。 如何在一次称重中确定假货?
有必要比较这些硬币中的任何两个,如果它们相等,则第三个硬币为假。
5)如果我们有3个硬币,并且不知道,那么伪造就更难或更容易。 是否可以在一称重中确定假货?
不幸的是,没有。
6)如果我们有4个硬币,而未知的伪造品更难或更轻,我们能否在一次称量中确定伪造品?
不幸的是,没有。
7)如果我们有4个硬币,并且不知道是假的还是假的或更轻,您可以确定多少个假货?
两次称重。
接下来,从基本案例中,我们收集8、9、10、11和12个硬币的情况。 您如何看待解决方案?
以下是完整的解决方案。
3.决定第一步:将硬币分成3组,每组4组:1 2 3 4,5 6 7 8,9 10 11 12。
比较前两组。 三种选择是可能的:
- 第一组较重;
- 第二组较重;
- 相等。

1)如果组数相等,则假硬币在第三组中。 有必要在两次称重中找到4个硬币的假硬币。
将第三组分为两部分:9 10 11 12
比较9和10:
- 如果相等,则第二组中的假硬币-比较9和11。如果9和11相等,则假-12,如果不是-11
- 如果它们不相等,则在第一组中为false-比较10和12。如果10和12相等-false-9,否则为-10。
因此,我们发现了假硬币。
2)考虑第二种情况。 如果第一组比第二组重,那么我们给第一组分配符号“>”,第二组分配符号“ <”,第三组分配“ 0”。
我们将硬币分为1 9 10 11和5 2 3 4组,称重。 三种选择是可能的:
- 相等。 伪造的硬币在数字中:6 7 8.比较6和7,如果它们相等,则伪造为8,如果6更大,则伪造-7,如果7更大,则伪造-6,因为在这种情况下,伪造的硬币更容易。
- 第一组较重,然后假硬币为1或5。如果它们相等,则比较1和9-假硬币-5,否则-1。
- 第一组比较容易,然后在硬币2 3 4中伪造,因为已知9、10和11是真实的,而第二组仅比硬币2、3和4更为重要。比较2和3,如果它们相等,则伪造4,如果2重,则假为2,否则3rd为假。
3)第二组比第一组重的情况与第二组相似。
决策树的总图如下所示。
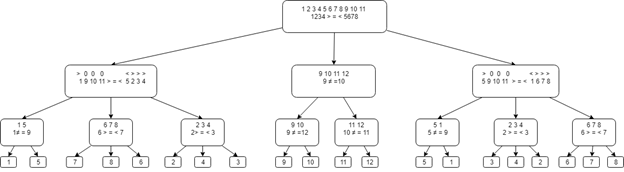
结论当任务到达以进行修订或调试时,最好采用上述方法:
- 决定给出什么?
- 哪些基本案例/任务可以分解?
- 有什么未知的问题可以解决? 需要进行哪些实验来减少熵?
- 快跑
- 问题解决了吗? 不行吗 返回步骤1。
成功的解决方案。