哈萨克斯坦公司股价的VaR和ConVaR估计

在过去的几十年中，世界经济经常陷入影响每个国家的金融危机漩涡。 由于这一事实，几乎几乎导致了现有金融体系的崩溃，数学和经济建模方面的专家都已开始使用控制金融世界中资产和投资组合损失的方法（路易斯安那州莱希纳和美国奥瓦特（2010）。对经济过程进行数学建模以预测市场行为并对其可持续性进行评估的趋势正在增加（同上），无需控制和正确评估威胁，每个人都知道它能够触发组织发展的巨大成本，甚至破产。

风险价值（VaR）最终已成为在金融部门及其监管机构中捕捉风险的常规方法（Engle，R.和Manganelli S.，2004）。 该模型最初用于估计给定时间段内和给定出现概率下投资组合中的损失值。 除了在金融部门使用VaR的事实外，还有许多在不同领域评估风险价值的例子，例如期望医护人员发展医疗资源管理Zinouri，N.（2016）。 尽管在实际实验中应用了原始性，但该模型仍存在评估缺陷（同上）。

该报告的目的是描述现有VaR模型，包括其升级版本之一，即条件风险值（CVaR）。 在下一部分和第3部分中，将说明模型的评估算法和测试。 为了生动地说明这一点，预期损失是根据哈萨克斯坦一家公司在很长一段时间内在金融证券交易所市场上交易的资产估算的。 最后的第4和第5节讨论并演示了研究工作的结果。

背景知识

据信，直到40年前，大型金融机构才首次使用VaR，因此VaR在其他贸易公司中也很流行，甚至金融监管机构也对该模型有所关注（Linsmeier，TJ和Pearson，ND 2000）。 例如，美国证券交易委员会在1997年将VaR列在计算市场风险和财产的定量方法清单上（同上）。

实际上，根据路易斯安那州Lechner和TC的Ovaert（2010）以及Ts的Linsmeier和ND的Pearson（2000）的文章，VaR是一个以货币单位表示的估计方程，不会超过损失幅度范围在给定的时间段和给定的置信度下。 通常，模型估计的置信度（99％，97.5％，95％），或者换句话说，将发生一些不利情况并对市场产生影响的概率等于1％，2.5％和5％（同上）。

可以描述著名的VaR方程（Phelps S，2018）：

$$$（1）\ VaR（X）= \ min \ \ {x \ \ epsilon \ R：1-F_x（-x）\ geq \ alpha \}$

其中X是执行投资组合价值总额的随机变量，并且是累积分布函数（同上）。

另一方面，Hooper GP（1996年，引用于洛杉矶Lechner和Ovaert，TC 2010引用）用非常基本的方式表示了具有置信度alpha定义的VaR：

$$$（2）\ VaR ^ \ alpha（X）= \ sigma \ sqrt {\ delta t} N ^ {-1} \ alpha$

哪里 $$$\ sigma$是选定股票收益的标准差， $$$\增量t$是固定时间段的平方根，并且 $$$N ^ {-1}$是正态分布的累积分布函数（CDF）（Lechner，LA和Ovaert，TC 2010）。

尽管VaR是估算已决定的投资组合风险的众所周知且易于处理的方法，但在衡量对最终市场问题的脆弱性的情况下仍存在不足之处，即该示例与极端市场事件未完全被抓住的可能性有关。正态分布（Capiński，MJ 2015）。 为了解决此问题，创建了“条件风险值”（CVaR），它考虑了预期损失值而不是VaR（同上）。 CVaR定义为：

$$$（3）\ CVaR ^ \ alpha（X）= \ frac {1} {\ alpha} \ int ^ \ alpha_0 VaR ^ \ beta（X）d \ beta = \ frac {-1} {\ alpha} q ^ \ beta（X）d \ beta$

$$$（4）\ CVaR ^ \ alpha（X）=-\ frac {1} {\ alpha}（E [X 1 _ {\ {X \ leq q ^ \ alpha（x）\}}] + q ^ \ alpha （X）（\ alpha-P [X \ leq q ^ \ alpha（X）]））$

哪里安D.-H. et.al（1999，Capiński，MJ 2015引用）解释 $$$-q ^ \ alpha（X）$
X概率的X值的VaR $$$\ alpha$并定义为X的上分位数。

此外，Acerbi C.和Tasche D.（2002，引用于Capiński，MJ 2015）确认：“ CVaR是一种连贯的风险度量”。 Rockafellar，RT和Uryasev，S.（2000）注意到CVaR具有额外的功能：等价跃迁，正均匀，凸等。

本文的下一章演示了Rockafellar，RT和Uryasev，S.（2000）的工作中还宣布的众所周知的风险价值（VaR）和条件风险价值（CVaR）的实现，它们也被宣布为“预期缺口（ES）”。通过使用信息技术处理真实数据。

方法论

让我们考虑最常用的计算VaR的方法，以及它的优缺点。

根据Lechner，LA和Ovaert，TC（2010）的报告，历史模拟是评估VaR及其修改方法的广泛方法。 在数据的历史建模中，我们采用投资组合的财务波动值，这些值已从过去的测量中得知。 因此，只有逻辑上的顺序是，该方法的缺点是不可能在没有任何信息的情况下建立投资组合的预测。 蒙特卡洛方法在很多方面与用于高精度技术的历史建模方法相同，主要的区别在于蒙特卡洛模拟的计算不是基于真实数据，而是基于随机生成的值。 这种方法的优点是可以考虑多种情​​况，并在极端条件下模拟市场行为，并且无需在风险因素和投资组合变化之间进行近似估算（Glasserman，P.，Heidelberger，P和Shahabuddin，P.，2002年）。 明显的缺点是实现此方法所需的大量计算资源（同上）。

当然，这些并不是计算VaR模型的唯一方法。 此外，价格预测有简单的线性模型和二次模型，还有相当复杂的价格变动方法，本文没有介绍。

资料分析

作为测试准确评估的辅助数据，我们提取了KAZ Minerals的库存。 为了澄清工作，在模型中采用调整后的收盘价进行模拟。 KAZ Minerals公司的股票（KAZ.L）是哈萨克斯坦公司在伦敦证券交易所（LSE）上成功交易的证券之一，并且被归类为高级股权商业公司名单（London Stock Exchange，2019）。 该实体表示自己是哈萨克斯坦的大型铜矿开采公司（Kazminerals.com.2019）。

股价的历史数据可从Yahoo Finance网站（Finance.yahoo.com，2019）下载。 为了确保工作的有效性，我们观察了从2018年3月22日到2019年3月22日的一年时间。 此外，为避免信息中断，在分析中，由于Microsoft Excel程序（Excel）兼容CSV格式，因此以逗号分隔值（CSV）格式下载了KAZ.L股价的历史数据。 。 使用图1中的Excel，将项目的选定数据显示为折线图。

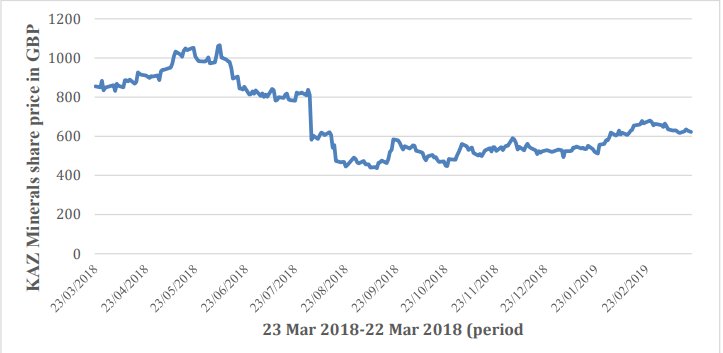
图1.一年中KAZ Minerals股票价格变化的动态

由于报告时间轴的局限性，因此没有在Excel中使用像Python这样的编程语言来实现评估模型，而是完全对数据进行了分析。

调查结果

在上一节中，这些模型基于VaR和CVaR方程预测了投资组合的潜在损失，并使用了从2018年3月23日至2019年3月23日KAZ Minerals股价变化的模型，这些模型可从官方网站Yahoo Finance（Finance.yahoo）下载。 com，2019年）。 这两个方程式针对所选期间的每个日期执行。

表1展示了此示例的平均每日业务收益，收益的标准偏差，收益的最小值和收益的最大值。

表1.份额平均收益率和收益率标准差

选定的唯一安全性KAZ Minerals的相应平均值为-0.0006，回报的标准偏差为0.0355。 而且收益的方差是0.0013。 此外，应该特别强调的是，在Vee，DNC和Gonpot，P. N（2014）的研究工作中，哈萨克斯坦的股票收益率显示出显着的波动性价值，但是估计值与哈萨克斯坦证券交易所早前和之后的指数有关应当注意，在损失分配中，收益之间的最大值为0.0998，收益之间的最小值为-0.2829。 表2列出了2018年3月23日至2019年3月22日在伦敦证券交易所英镑（GBP）交易中的调整后收盘价（KAZ.L）中的最大值和最小值。

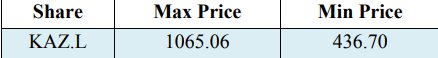
表2. KAZ Minerals的最大和最小股价（英镑）

下一步是对置信度0.99、0.972和0.95的评估风险价值（VaR）和条件风险价值（CVaR）。 这些值在表3中显示。

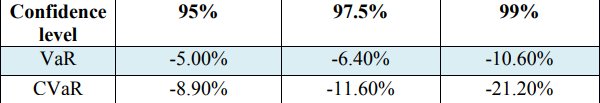
表3.收益的VaR和CVaR值

从一年的2018年3月23日到2019年3月22日，抽取了252个模拟样本。

讨论区

在报告中，VaR和CVaR方程式在短期模型中证明了哈萨克斯坦公司股价的估计模型的可信值。 一方面，使用这些值，两种方法都可以提供足够的结果来评估投资组合威胁的价值（Linsmeier，TJ和Pearson，ND 2000； Lechner，LA，Ovaert，TC 2010）。

此外，根据表2的发现，下一个通知很明显，即与所有置信度度量相比，VaR值比CVaR值更大。 CVaR承担选择的投资组合平均风险的事实可以对此作出解释，因此，与VaR相比，CVaR在损失分布的尾部更加敏感。 这再次证明了CVaR是一个连贯的风险（Acerbi C.和Tasche D.，2002，在Capiński，MJ 2015中引用； Rockafellar，RT和Uryasev，S.2000）。 例如，关于两个估计模型的充分性，置信度为99％，VaR和CVaR说明了股票收益损失的显着百分比。 准确地说，可能检测到VaR为-10.60％，CVaR为-21.20％。 很明显，在一定的置信水平下，CVaR之所以采取巨大措施的原因是由于该期间的股价范围，最高价格分别为1065.06英镑和最低股价分别为436.70英镑。

结论

考虑了上述所有内容后，显然应该再次提到该报告的目的是证明哈萨克斯坦公司（KAZ Minerals）在2018年3月23日至2019年3月22日期间可能损失的价值估计。由风险价值（VaR）和条件风险价值（CVaR）等式形成。 将模拟的性能在相同时间段内相互比较。 结果显示了每种方法的重要价值，并证明了以前在同一领域进行的工作，与VaR相比，CVaR具有更准确的测量值（Acerbi C.和Tasche D.，2002；引自Capiński，MJ，2015； Rockafellar，RT，和Uryasev，S.2000）。

尽管有批评，但VaR至今仍是所有金融机构中广泛使用的工具，其修改版本范围很广。 由于深入研究中复杂计算的障碍，该实验是通过使用Microsoft Excel而不是使用Python之类的编程语言来完成的，并且结果在报告中有所披露。 这篇论文的结果可以为在证券交易所，保险业和投资业中对投资组合使用复杂的风险评估方法进行进一步工作奠定基础。