下面我们将以线性微分方程的形式介绍数学模型的离散时间替代方法,这是众所周知的,但对于工程师来说却是出乎意料的,即自回归模型-移动平均,以及这种建模的非常不寻常的前景,其功能大大超过了您习惯从LDU获得什么。
该技术的潜在功能列表包括对无法观察到的进入干扰的系统进行分析,确定此类系统的共振特性,频谱和外部激励过程,通过短时间实现对过程的频谱估计,对低采样频率随时间变化的系统行为进行建模等。

经济学家(更准确地说是“计量经济学家”)众所周知的ARMA流程,对自动调节的专家了解较少,我认为,机械工程师和无线电电子工程师,尤其是“老派”工程师几乎不使用ARMA流程。 本文试图指出ARMA理论在工程实践中的一些可能应用领域。
简而言之,对于那些不熟悉该主题的人,实际上是关于它的。 出于明显的“数字”原因,随机连续时间过程x(t)在实践中通常将离散时间序列x [i]与采样间隔Δt匹配。
原则上,对于任何过程x [i],形式的表示都是可能的
x [i]-a 1 ·x [i-1]-a 2 ·x [i-2]-...-a p ·x [ip] = b 0 ·f [i] + b 1 ·f [i- 1] + ... + b q ·f [iq] (1),
其中
k和b
k是常数(对于该模型)系数,称为自回归移动平均模型,其阶数为自回归p和移动平均值q。 或ARMA(p,q)模型,f [i]是一种“传入”过程,大约要低一点。 通常(1)的书写形式略有不同(6)。
基本上,它只是具有递归AR和非递归MA部件的数字滤波器。
ARMA(p,q)模型与线性系统(例如,机械系统)之间存在对应关系,例如,由以下形式的众所周知的线性微分方程描述
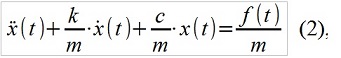
其中,m,c,k是机械系统的质量,刚度和阻尼,f(t)是外力。 ARMA副本如下所示:
x [i]-a 1 ·x [i-1]-a 2 ·x [i-2] = b 1 ·f [i-1] (3),
通过线性系统的特征值λ1和λ1 *(为简便起见,考虑“振荡”情况)可以很容易地找到模型的系数:
a
1 = z + z *,a
2 =-z·z *,b
1 = j(z * -z)·Δt/(2mω1),
其中z = exp(λ1·Δt),λ1 =-ε1 +jω1,j是虚部,*是复共轭
供参考:

对于测试系统,m = 1 kg,c = 100 N / m,k = 0.75 kg / s,Δt= 0.12 s,
获得ARMA(2,1)-模型
x [i]-0.69433x [i-1] +0.91393 x [i-2] = 0.010696f [i-1](关于如何从(2)获得(3)的简短说明。线性系统的脉冲转换函数,即系统对单个脉冲的响应:
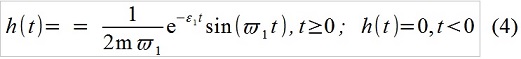
以“积分”形式的记录(2)称为“卷积” f(t)和h(t),这意味着它将外部作用视为基本脉冲序列。 在不连续的时间里,例如编写如下:
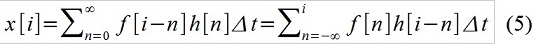
通过使用选定的因子1,a
1和a
2将x [i],x [i-1]和x [i-2]相加
,它们实现了无限“尾巴” h [i]的相互an灭-右边的是f [i] ·H [0] = f [i]·0和f [i-1]·h [1] = f [i-1]·b
1 。 从ARMA理论的角度来看,移动平均数MA(∞)的无穷维模型被转换为ARMA(2,1)(尽管有人会说是偶然获得了纯自回归模型AR(2)= ARMA(2,0)。
备注1.熟悉过程数字处理的读者会说,仅离散化h(t)并不是很正确-有必要将函数h(t)的频率限制为1 /(2Δt)(以进行过滤)。 否则,将出现频率屏蔽错误。 我们系统的频率响应和相位响应(“分析”模型和ARMA模型)的图形显示了为什么在大多数工程案例中最有可能忽略此误差的原因(图1)(此处,频率响应为对数刻度)。
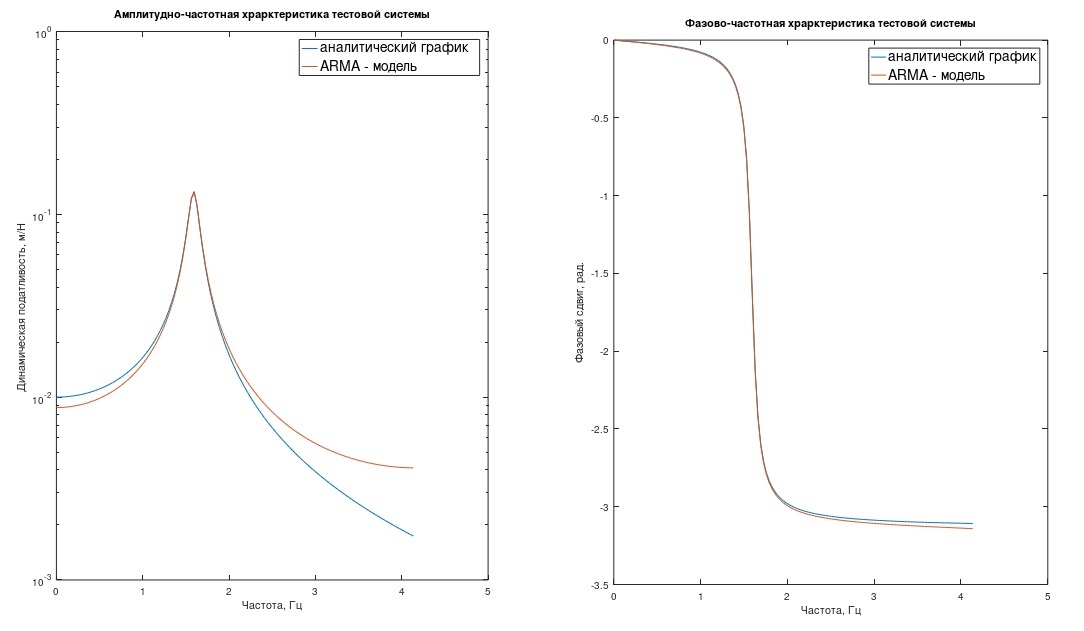
图1测试系统的频率响应和相位响应
备注2.实际上,由于机械系统的几个自由度或实际外部影响的复杂范围,ARMA模型的阶数可能比上述示例大得多。
备注3.非常重要。 在假设的情况下,有一些方法(此处未考虑-可以写更多文章),它们只能通过所得过程x [i]来估计ARMA模型的参数(即p和q模型的阶数以及系数a
k和b
k )。 f [i]是假设的白噪声,其方差也可以估算。 通常,这种评估是整个ARMA理论的主要部分。 尽管这些方法没有特别的完善,但它们引起了人们的极大兴趣。
现在说明为什么实际上所有这些都可以(或可以)应用于实践中。 除了非常明显的-从头两个点和两个系数a
1和a
2快速构建“手动”阻尼(和非阻尼)正弦波之外,在我看来,这些模型在工程实践中的应用更为严格。
1.好吧,实际上,为了模拟系统的运行-我们给输入一个真实的外部信号f [i],在输出端得到x [i]:
x [i] = a 1 ·x [i-1] + a 2 ·x [i-2] + ... + a p ·x [ip] + b 0 ·f [i] + b 1 ·f [i- 1] + ... + b q ·f [iq] (6)
ARMA模型比有限差分模型更好地处理任务,但是,这仅在较大的采样间隔Δt时才明显。 (在图2中,Δt= 0.12 s(左)和0.03 s)。 在什么情况下,与ARMA混为一谈-您可以决定。
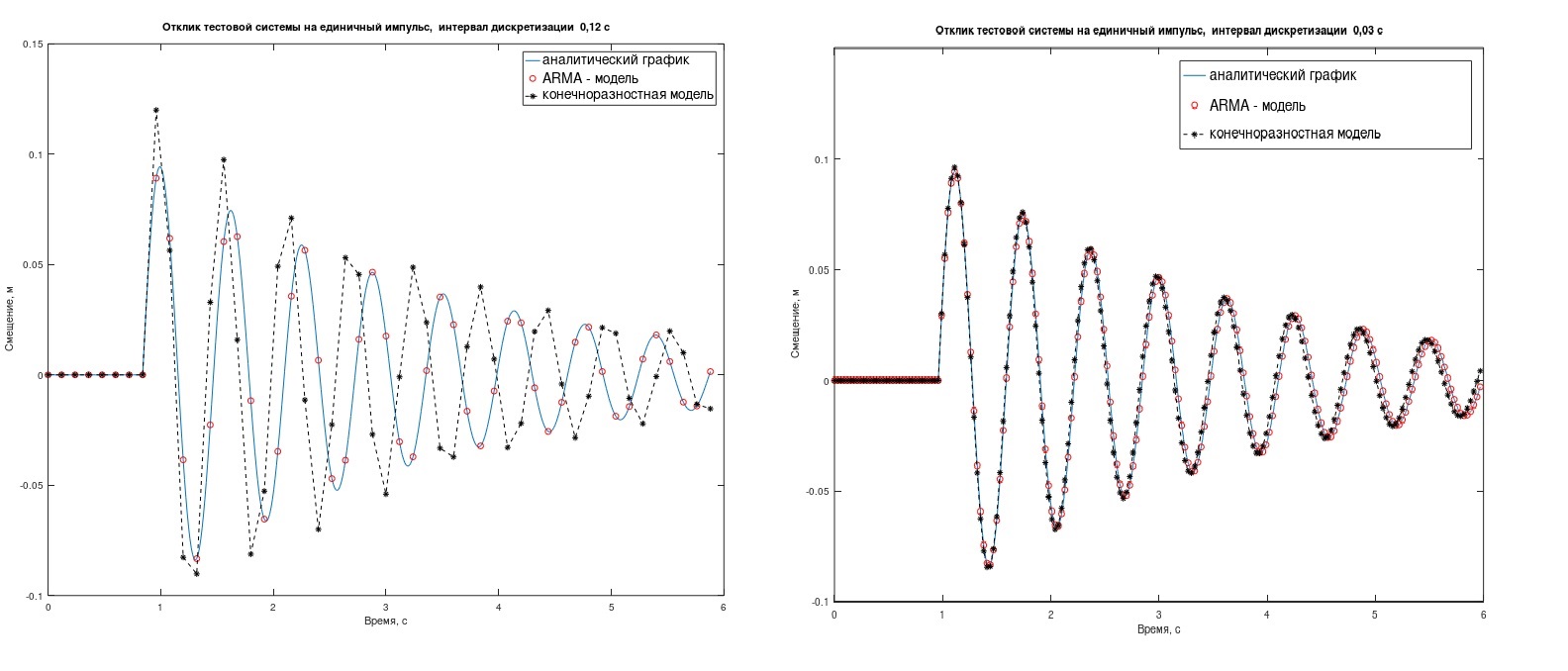
无花果 2.测试系统对单个脉冲的响应。
2.用于频谱估计,尤其是在固定过程的实施长度不足以进行观察时。 也许这是ARMA模型最著名的工程应用。 由于将为所研究的过程获得某个数字滤波器和白噪声的方差,因此以明显的方式解决了构建PSD估计的任务。 确实,有可能在外部获得非常“平滑”的SPM图,同时创造出高分辨率的印象。 评估的预期改进与以下事实有关:研究人员通常通过设置已知的模型顺序将有关过程性质的外部信息带入评估的构建。
简而言之,您需要知道此PSD的外观。 使用经典方法对该实现方式进行的“探索性”研究几乎无济于事,主要是指具有类似性质的经典(基于FFT)研究,但实现时间要长得多。 可能会出现严重错误。
3.在无法观察到真正的外部效应的情况下,用于分析系统的共振特性和外部作用的频谱。 如已经指出的,知道过程x [i],就可以确定模型a
k和b
k的所有系数(以及输入白噪声的方差)。 使用它们,确定具有相应系数的两个多项式的根,很容易找到模型的p个“极点”和q个“零点”(λk和μk)并构造其传递函数-您甚至可能无法使用ARMA形式(此处给定),并以通常的“分析”形式-如我们在上面发现的(图1),差异很小。 例如,对于p = 5,q = 3(虽然从现有的p和q之比的限制中抽象出来),作为选择,我们有:
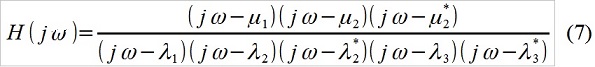
当然,一切都非常非常简单。 根据研究对象的已知性质(例如,对汽车行驶平顺性的多边形测试)和外部冲击(道路的微观轮廓),研究人员决定重写传递函数,例如,如下所示:
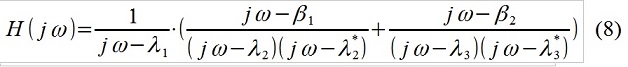
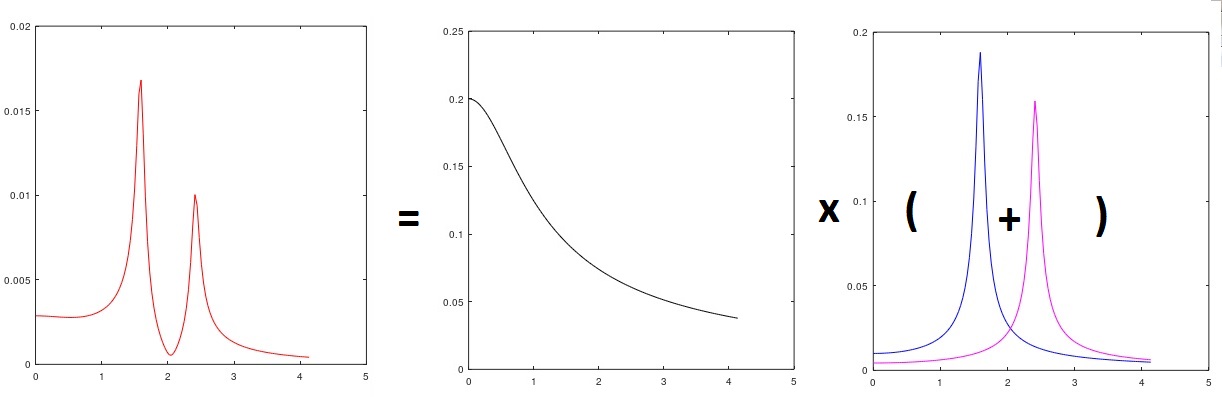
图3信号频谱与输入干扰的分配分析
并评论说-模型中与λ1相关的部分显然是道路的“粉红色”微观轮廓(图2所示的平方和乘以传入的假设白噪声的方差)(也就是说,我们识别了未知的实谱)在手动选择的输入信号上,“λ2”和“λ3”是物体在悬架上的共振特性(可能是纵向-角度和垂直振动模式)。 当然,主要问题将在于确定ARMA模型的参数。 对于刚刚描述的情况,有时您可以不使用任何ARMA,即可按照光谱密度图以老式方式(尽管以电子形式)“爬网”并在-3 dB的水平上测量峰值宽度等,或者进行弯曲,有时即使取得了很大的成功。
3.对于线性预测x [i]。 显然,ARMA的主要应用是计量经济学家。 从(6)可以看出,如果可以使用上述方法估计模型的系数,则下一个值x [i]可以精确地估计为观察不到的假设白噪声b
0 ·f [i],则可以估计该白噪声的方差连同模型的系数。 通常在这种情况下,暗含了对模型参数的动态(实时)调整。 显然,它在主动振动和降噪系统中很有用。 TAP专家最清楚。
4.恢复无法观察到的无法访问的进程。 如上文第3节所示,将模型分为多个部分时,根据对所研究过程的性质的了解,可以分别评估传入扰动的频谱和物理系统的振荡特性(将模型分为多个部分)。 您可以走得更远-创建一个过滤器(ARMA模型,原始模型的逆模型),将系统的输出与输入连接起来,并在所得过程x [i]的帮助下获得传入干扰的临时实现。 例如,尝试通过单独的研究(例如,通过遥测获得)无法访问的设备来恢复以精确未知的线性失真记录的未失真信号。
基于我的谦虚知识,我将表达这样的主观判断。 ARMA技术对工程问题的适用性在很大程度上取决于从结果信号估计这些模型的参数的方法的完善,或者,我认为,这些方法的不完善性极大地限制了这些方法。 积累ARMA在工程中的应用经验似乎是有意义的,主要是因为预期该领域将有一个非常可能的“突破”。