前言

我认为我们需要简要地解释一下，为什么在能源预算的计算中突然出现了一个看似微不足道的话题，以及为什么正是CubeSat卫星呢？ 好吧，这里的一切都非常简单：我的简短教学实践向我表明，尽管这个话题很基本，但是第一次所有人都还不了解这个主题，而且，在初次阅读时，有几个问题并不明显。 而且，似乎在这些基本的东西上他们仍然在IEEE上发表文章，而这远非学生所能完成。 为什么是CubeSat？ 这里的方法仍然更简单：卫星格式很有趣（事实证明，存在微卫星和纳米卫星的事实使许多卫星陷入了短暂的震动状态），因此非常适合用于教育目的。

出于与我在之前的出版物中所述相同的原因，将在python 3中进行仿真。 我们将考虑低轨道情况（LEO-低地球轨道），并实际上计算接收器通过下行链路（DL-下行链路）输入的信噪比（SNR-信噪比）。 为了清楚起见，我们将使用开放访问中的几个目录并构建图形。

所有源代码都可以在我的GitHub存储库中找到 ，我邀请所有感兴趣的人阅读它！ 我将非常感谢代码审查和建设性的批评！

走吧

我们将计算什么公式？

首先，当然，这是一个众所周知的公式，它以对数标度（简单地以分贝为单位）对所有人（涉及该主题）信噪比，在此我们考虑了所有可能的损耗和放大并具有一定程度的抽象：

在哪里 -热噪声的总功率（与噪声的频谱密度具有已知关系 ），以dBm（分贝/毫瓦）为单位， -以dBm为单位的发射功率， 和 -分别在发射机和接收机一侧的天线增益（以dBi-各向同性分贝为单位）， 和 -发射机和接收机馈线的增益（以dB为单位）， 和 -馈线损耗（以dB为单位）， 电磁波传播路径中的损耗，以dB为单位， -以dB为单位的额外损耗（可以说，有些余量）。

通常，前七个术语或多或少是清楚的：这些是​​参考数据。 在此过程的最后三个参与者中，事情变得更加有趣。

热噪声功率

如您所知，这种电子设备的祸害无处躲藏，您只能考虑到：

在哪里 -玻尔兹曼常数 -等效噪声温度， -天线损耗和天空噪声（背景）的总和， -接收器的噪声温度（ 和 -噪声系数，可以从噪声图片估算（ -接收天线的噪声系数），以及 -噪声频带的宽度。 您可以将噪声带设为等于接收器本身的带宽 但是，根据[1，p。98]，噪声带宽 可以更准确地定为 在哪里 -从1.002到1.57的常数（与接收器配置有关）。

额外损失

在这里，您可以从相同目录中获取某种有保证的供应（通常情况下是收集的），或者更深入地自己计算所有内容。

在本节中，我几乎完全依靠旧的康托尔教科书，即教科书的这一部分[1，p。88-96]。 如果读者有更多相关的权威资料-请分享，我认为这对每个人都会有用。

我们主要注意的是：

1. 由于天线指向的折射和不精确造成的损耗 （ 天线波束损耗 ）

被指定为 在哪里 -光束宽度和 -半功率的波束宽度，无论猜测有多困难，都取决于某些天线设备的特性：

1. 大气相位效应

如果您相信经典，那么由于接收器的带宽，这些损耗将主要影响数据传输速率，因为建议根据表1 [1，p。1]选择频带。 91]。 避免相位失真。

标签 1.不同范围的最大接收器带宽。

虽然，应该指出的是，由于热噪声，这些数字非常令人印象深刻，通常不予考虑。

1. 天线极化失配造成的损耗

可以根据椭圆率系数进行估算 $$$e_1$和 $$$e_2$（我附上图1中的苏联书摘录）。

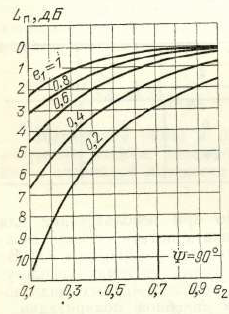
图1。 发射和接收天线之间的极化不匹配所引起的损耗取决于椭圆率。 [1，p。 93]

但是，我遇到了此参数作为参考。 例如，在计算NanoCom AX100的能量预算时，极化损耗为3 dB（大气损耗为2.1 dB，电离层损耗为0.4 dB）。

1. 大气衰减

我们可以根据ITU的建议评估这个有趣的参数，也可以自己计算。 幸运的是，这里有一些特殊的库。

沿电磁波传播路径的衰减（路径损耗）

事不宜迟，我们以Friis公式开头 ：

在哪里 -电磁波长（以已知方式与载波频率相关 ， 是电磁波的速度（光速，如果更简单），并且 -卫星与地面站之间的距离。

在这里，我们也许会想到一个最有趣的问题：计算应该走多远？ 正如引言中已经提到的那样，我们正在考虑LEO卫星，这意味着我们所谓的卫星正在相对于地球移动（与地球静止的情况相反，在这种情况下，卫星实际上悬在一个点上）。

当然，如果假定通信卫星的轨道大致位于地面站的“上方”，则可以通过将该方案作为基础（图2）来尽可能地简化所有操作。

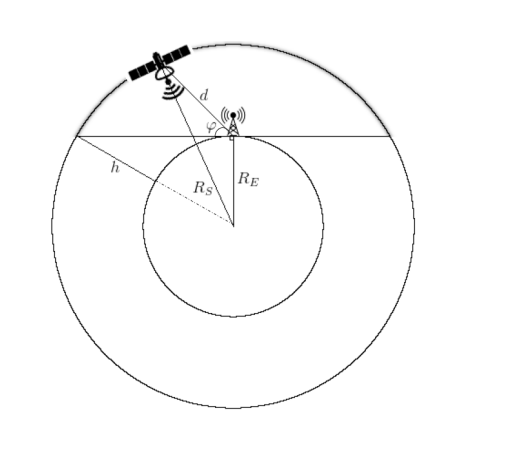
图 2.低地球轨道[2]中CubeSat轨迹的示意图。

然后可以通过以下公式计算距离：

在哪里 -实际上，有地球的半径， -卫星轨道高度，以及 -仰角。

但是，您可以多做一些，再次转到经典的（已经有所不同）[3，第110-123页]，然后计算已经相对于地面站的真实地理坐标的所有内容（
和 ）以及卫星的实际位置（瞬时上升节点- 和轨道极-瞬时轨道极 ） 准备好了，将会有很多三角函数：

在哪里 -地球的最小中心角， -最低天底角 是地球的角半径。 可以通过以下方式计算最大距离：

在哪里 和 （ -最小卫星仰角）。

总结一下参数的简短摘要 ：

1. 我们选择什么作为起点 ：载波频率，轨道高度（也许卫星的位置和地面站的地理坐标-取决于我们想要获得的精度）；
2. 我们发现与设备有关且可调的参数 ：发射功率，接收器带宽，
3. 我们找到了参考数据 ：天线增益和损耗，馈线增益和损耗，噪声温度，附加损耗。

我们模拟结果

作为下行链路评估的技术参数来源，我们提供了适用于CubeSat卫星的收发器和天线的实际示例，例如NanoCom AX100和NanoCom ANT430 。 对于更大的带宽，当然最好考虑S波段 。 NanoCom ANT2000贴片天线和NanoCom SR2000收发器可用于此范围。

我们开始检查发生了什么。

from SmallSatLB import * import pandas as pd 

所有逻辑有条件地分为两个选项： 'draft' ，其中公式（4）用于计算距离； 和“精确” ，其中使用公式（5）和（6）。

“草稿”

 l_d = LinkBudget(750*1e3, 'draft') #   (   ) d = l_d.distance() #   phi = np.pi*np.array(range(0,181,5))/180 #     plt.plot(180*phi/np.pi, d*1e-3, '-o') plt.title('Distances') plt.xlabel('Elevation angles (degrees)') plt.ylabel('Distance (km)') plt.grid() 

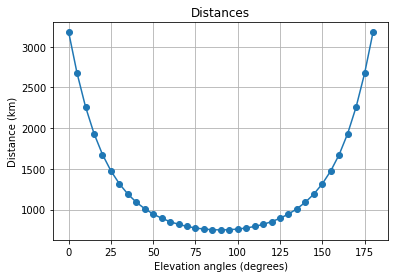
 snr, EIRP = l_d.expected_snr(2.4e9, 1, 7.3, 35, 1.5e6, 1000) #  SNR plt.title('Expected SNRs') plt.xlabel('Elevation angles (degrees)') plt.ylabel('SNR (dB)') plt.legend() plt.grid() 

美女！

“精确”

 l_p = LinkBudget(750*1e3, 'precise',\ L_node = 100+90, incl = 90 - 61.5,\ lat_gs = 22, long_gs = 200, eps_min = 5) snr, EIRP = l_p.expected_snr(2.4e9, 1, 7.3, 35, 1.5e6, 1000) print(min(snr)) print(max(snr)) 

 >>> 5.556823874020452 >>> 8.667000351847676 

总的来说，这里是：我们有一个小的工具来进行主要的“估计”，并计算从卫星到地球（反之亦然）时信号将减弱多少。
谢谢大家的关注！

二手文献清单 ：

1. Kantor L. Ya。，Askinazi G.B. 卫星通信和广播：参考书 。 -无线电和通讯，1988年。
2. Otilia Popescuy，Jason S.Harrisz和Dimitrie C.Popescuz，《设计用于纳米卫星CubeSat任务的通信子系统：操作和实施的观点》，2016年，IEEE
3. Wertz JR，拉森WJ空间任务分析与设计，空间技术图书馆。 -Microcosm出版社和Kluwer学术出版社，美国加利福尼亚州埃尔塞贡多，1999年。