宇宙航行日快乐! 我们交给了印刷厂一本
“关于黑洞的小书”。 正是这些天,天体物理学家向全世界展示了黑洞的外观。 巧合吗? 我们没有想到;)因此,等等,很快,一本惊人的书将出现,由斯蒂芬·加布瑟和弗朗斯·普雷托里乌斯(Frans Pretorius)撰写,由奇妙的普尔科沃天文学家(又名Astroded Kirill Maslennikov)翻译,传说中的弗拉基米尔·苏丁(Vladimir Surdin)进行了科学编辑,轨迹基金会支持了该书的出版。
摘录下的“黑洞的热力学”。
迄今为止,我们一直将黑洞视为超新星爆炸期间形成的天体或位于星系中心的天体。 我们间接观察它们,测量靠近它们的恒星的加速度。 LIGO接收器于2015年9月14日进行的著名引力波记录成为黑洞碰撞更直接观测的一个例子。 我们用来更好地理解黑洞性质的数学工具是:微分几何,爱因斯坦方程以及强大的分析和数值方法,用于求解爱因斯坦方程并描述黑洞产生的时空几何。 并且,一旦我们能够对黑洞产生的时空进行完整的定量描述,从天体物理学的角度来看,黑洞的话题就可以被认为是封闭的。 从更广泛的理论角度来看,仍有许多研究机会。 本章的目的是讨论现代黑洞物理学的一些理论成就,其中将热力学和量子理论与广义相对论结合在一起,从而产生了意想不到的新概念。 基本思想是黑洞不只是几何对象。 它们具有温度,具有巨大的熵,并且可以表现出量子纠缠的表现。 我们对黑洞物理学的热力学和量子方面的讨论将比前几章中对黑洞中的纯粹几何时空特征的分析更为粗略和肤浅。 但是这些方面,尤其是量子方面,是正在进行的黑洞理论研究的重要组成部分,我们将非常努力地传达,即使不是复杂的细节,也至少是这些作品的精神。
在经典的相对论一般理论中-如果我们谈论爱因斯坦方程组解的微分几何-黑洞实际上是黑的,意味着什么也无法摆脱。 史蒂芬·霍金(Stephen Hawking)表明,当我们考虑量子效应时,这种情况将完全改变:黑洞最终会发出一定温度的辐射,称为霍金温度。 对于天体大小的黑洞(即从恒星质量的黑洞到超大质量的黑洞),与宇宙微波背景温度相比,霍金温度可以忽略不计-辐射充满了整个宇宙,顺便说一句,辐射本身可以被视为霍金辐射的一种变体。 Hawking确定黑洞温度的计算是该领域中更广泛的研究计划的一部分,该计划称为黑洞的热力学。 该程序的另一个主要部分是对黑洞熵的研究,该熵表征了黑洞内部丢失的信息量。 普通物体(例如一大杯水,一块纯镁或一块星星)也具有熵,黑洞热力学的主要陈述之一是,这种大小的黑洞比任何其他可以容纳在其中的物质都具有更大的熵。面积相同的区域,但没有形成黑洞。
但是,在深入讨论与霍金辐射和黑洞熵有关的问题之前,让我们快速浏览一下量子力学,热力学和纠缠领域。 量子力学主要是在1920年代发展的,其主要目的是描述非常小的物质粒子,例如原子。 量子力学的发展导致了诸如粒子的精确位置之类的物理学基本概念的侵蚀:例如,事实证明,当电子绕原子核移动时,其位置无法精确确定。 取而代之的是,将所谓的轨道分配给电子,在这些轨道中,它们的实际位置只能在概率意义上确定。 但是,出于我们的目的,重要的是不要过快地解决问题的这一方面。 举一个最简单的例子:氢原子。 它可以处于某个量子状态。 氢原子的最简单状态称为基态,是具有最低能量的状态,并且该能量是精确已知的。 从更广义的意义上讲,量子力学使我们(原则上)绝对准确地知道任何量子系统的状态。
当我们问有关量子力学系统的某种问题时,概率就出现了。 例如,如果可以肯定地知道氢原子处于基态,我们可能会问:“电子在哪里?” 并根据量子定律
力学,我们只能对这个概率进行一定的估计,大概是这样的:“电子可能位于距氢原子核最远半个埃的位置”(一个埃等于
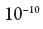
米)。 但是我们有机会通过某种物理过程找到比一埃更精确的电子位置。 这个过程在物理学中非常普遍,它包括将波长非常短的光子发射到电子中(或者,正如物理学家所说,将光子散射到电子上)-之后,我们可以在散射时重建电子的位置,其精度近似等于波长光子 但是此过程将改变电子的状态,因此此后它将不再处于氢原子的基态且将没有精确定义的能量。 但是一段时间后,它的位置将几乎完全确定(准确地用于此光子的波长)。 对电子位置的初步评估只能在概率意义上进行,其准确度约为1埃,但是一旦我们对其进行测量,我们便确切知道它的含义。 简而言之,如果我们以某种方式测量量子力学系统,那么至少在通常公认的意义上,我们“强制”给它一个状态,该状态具有我们正在测量的量的某个值。
量子力学不仅适用于小型系统,而且(正如我们所相信的)适用于所有系统,但对于大型系统,量子力学规则很快变得非常复杂。 关键概念是量子纠缠,其中一个简单的例子就是自旋(旋转)概念。 单个电子具有自旋,因此实际上单个电子可以具有相对于所选空间轴向上或向下定向的自旋。 电子自旋是一个观察到的量,因为电子产生的磁场很弱,类似于磁条的磁场。 然后,向上旋转表示电子的北极朝下,而向下旋转表示电子的北极“朝上”。 可以将两个电子置于共轭量子态,其中一个电子具有向上的自旋,另一个电子具有向下的自旋,但是无法确定哪个电子具有哪个自旋。 实际上,在氦原子的基态中,两个电子完全处于这种状态,称为自旋单重态,因为两个电子的总自旋等于零。 如果我们在不改变它们的自旋的情况下分离这两个电子,我们可以继续宣称它们是自旋单峰,但是我们仍然无法说出它们各自的自旋。 现在,如果我们测量它们的旋转之一并确定其指向上,那么我们将完全确定第二个指向下。 在这种情况下,我们说背面是纠缠的-没有一个背面本身具有确定的含义,而它们一起处于确定的量子状态。
爱因斯坦非常关注纠缠现象:它似乎在威胁相对论的基本原理。 让我们考虑两个电子处于自旋单态的情况,当它们在空间中彼此远离时。 为了确定起见,让其中一个拿走爱丽丝,另一个拿走鲍勃。 假设爱丽丝测量了她的电子的自旋,发现它是向上的,而鲍勃没有测量任何东西。 在爱丽丝完成测量之前,不可能说出电子的自旋是什么。 但是,一旦她完成了测量,她便绝对知道鲍勃的电子自旋向下(与她自己的电子自旋相反的方向)。 这是否意味着她的测量立即将Bob的电子向下旋转时的状态转移到Bob的状态? 如果电子在空间上分开,怎么办? 爱因斯坦及其同事内森·罗森(Nathan Rosen)和鲍里斯·波多尔斯基(Boris Podolsky)感到,测量纠缠系统的故事是如此严肃,以至于威胁到量子力学的存在。 他们提出的爱因斯坦-波多尔斯基-罗森(EPR)悖论使用的思维实验与我们刚刚描述的结论类似:量子力学不能完全描述现实。 现在,基于随后的理论研究和许多测量,已经建立了一个普遍的观点,即EPR悖论包含一个错误,并且量子理论是正确的。 量子力学的纠缠是真实的:纠缠系统的测量将相互关联,即使这些系统在时空上相距甚远。
让我们回到将两个电子置于自旋单态并将其分配给爱丽丝和鲍勃的情况。 在进行测量之前,我们能对电子说些什么? 两者一起处于一定的量子态(自旋子态)。 茜素电子的自旋同样可能向上或向下。 更准确地说,其电子具有相同概率的量子态可以是一个(向上旋转)或另一个(向下旋转)。 现在对我们来说,概率的概念比以前具有更深的含义。 以前,我们考虑了某个量子态(氢原子的基态),然后看到一些“不舒服”的问题,例如“电子在哪里?”,这些问题的答案仅存在于概率意义上。 如果我们问“好”问题,例如:“这个电子的能量是多少?”,我们将得到某些答案。 现在,我们没有关于爱丽丝的电子的“好”问题了,答案不取决于鲍勃的电子。 (我们不是在谈论诸如“爱丽丝的电子有旋转能力吗?”之类的愚蠢问题?这些问题只有一个答案。)因此,我们将不得不使用概率语言来确定半混淆系统之一的参数。 只有当我们考虑爱丽丝和鲍勃可以询问其电子的问题之间的联系时,确定性才会出现。
我们特意从已知的最简单的量子力学系统之一开始:单个电子的自旋系统。 希望将基于这样的简单系统来构建量子计算机。 现在,单个电子的自旋系统或其他等效的量子系统称为量子位(qubit)(“量子位”的缩写),它强调了量子位在量子计算机中的作用,类似于数字计算机中普通位的作用。
想象一下,现在我们已经用一个复杂得多的量子系统替换了每个电子,该系统具有许多而不只是两个量子态。 例如,他们给了爱丽丝和鲍勃纯镁棒。 在Alice和Bob朝不同的方向前进之前,它们的条可以相互作用,我们将同意这样做,他们将获得一定的一般量子态。 一旦爱丽丝和鲍勃分开,他们的镁棒就会停止相互作用。 与电子的情况一样,每个条形都处于不确定的量子状态,尽管我们相信它们一起形成了一个完全确定的状态。 (在此讨论中,我们假定爱丽丝和鲍勃能够移动镁棒而不会干扰其内部状态,就像我们先前假定爱丽丝和鲍勃可以分离纠缠的电子而不会改变其自旋一样。)但是区别在于在这种思想实验和电子实验之间,每个条的量子态的不确定性是巨大的。 棒可能获得比宇宙中原子数更多的量子态。 这是热力学进入阶段的地方。 但是,定义非常不准确的系统可能具有某些定义明确的宏观特征。 这种特性例如是温度。 温度是系统任何部分具有一定平均能量的概率的度量,温度越高,能量越高的概率就越高。 另一个热力学参数是熵,它基本上等于系统可以采取的状态数的对数。 对于镁棒而言,另一个重要的热力学特性是其总磁化强度,即本质上是一个参数,该参数显示了自旋指向上方而不是自旋指向下方时棒中的电子数量。
我们将热力学纳入到我们的故事中,以此来描述其量子态由于与其他系统纠缠而无法确切知道的系统。 热力学是用于分析此类系统的强大工具,但其创建者根本没有想到这种应用。 萨迪·卡诺(Sadi Carnot),詹姆斯·焦耳(James Joule)和鲁道夫·克劳修斯(Rudolph Clausius)是十九世纪工业革命的领导者,他们对所有最实际的问题都感兴趣:发动机如何工作? 压力,体积,温度和热量是发动机的血肉。 卡诺(Carnot)发现,热量形式的能量永远无法完全转化为有用的工作,例如起重货物。 总是会浪费一部分能量。 克劳修斯(Clausius)为建立熵的概念做出了主要贡献,熵是一种确定与热相关的过程中能量损失的通用工具。 他的主要成就是意识到熵从不减少-在几乎所有过程中它都会增长。 熵增加的过程称为不可逆-恰恰是因为它们在不减小熵的情况下无法反向。 克劳修斯(Clausius),麦克斯韦(Maxwell)和路德维希·博尔兹曼(Ludwig Boltzmann)(以及其他许多人)进行了统计力学发展的下一步-他们表明,熵是对无序的一种度量。 通常情况下,您对某事采取的行动越多,就越容易陷入困境。 即使您开发了旨在恢复秩序的过程,在此过程中也不可避免地会形成熵,而不是破坏熵,例如释放热量时。 以完美的顺序堆叠钢梁的起重机在梁的位置方面产生了整齐有序的效果,但是在运行过程中会释放出太多的热量,总熵仍在增长。
但是,关于19世纪物理学家热力学的观点与与量子纠缠有关的观点之间的差异并不像看起来那样大。 每次系统与外部代理交互时,其量子状态就会与代理的量子状态混淆。 通常,这种纠缠导致系统量子态不确定性的增加,换句话说,导致系统可以存在的量子态数量的增加。 由于与其他系统的相互作用,通常会根据系统可用的量子态数量来定义熵。
通常,量子力学提供了一种表征物理系统的新方法,其中某些参数(例如,空间位置)变得不确定,而其他参数(例如,能量)通常是准确已知的。 在量子纠缠的情况下,系统的两个基本分开的部分具有已知的共同量子态,并且每个部分分别是不确定的态。 纠缠的标准示例是处于单重态的一对自旋,其中无法确定哪个自旋是向上的,哪个自旋是向下的。
在大型系统中,量子态的不确定性需要一种热力学方法,在这种方法中,尽管系统具有许多可能的微观量子态,但仍可以非常精确地知道宏观参数,例如温度和熵。, , , , . — , , , 2π. , , , ‑. , , , . : - ? , , , . , , 6 . , ( , ) . , 1,5 , . , , , , ; , , . , , . ( « , …», , , , .) , , : , , , , , , . , , , , , , , , . : ! , , , , , . , , , , , , . , -. , , - , .
在我们对量子纠缠的讨论中,我们已经习惯了这样一个想法,即即使一个量子力学系统整体上具有某个量子态,它的某些部分也可能没有。实际上,当我们讨论一个复杂的量子系统时,可以在热力学的框架内对其进行精确的描述:尽管整个系统的量子状态非常不确定,但可以将其归因于非常确定的温度。我们涉及爱丽丝,鲍勃和比尔的最新故事与此情况有些相似,但是我们在这里讨论的量子系统是空时空,而爱丽丝只看到了一半。我们保留的意见是,整个时空都处于基态,这意味着其中不存在粒子(当然,不包括爱丽丝,鲍勃,比尔和火箭)。但是,爱丽丝所见的时空部分将不会处于基态,而是会与她看不见的那部分相混淆。爱丽丝感知到的时空处于以有限温度为特征的复杂不确定量子状态。 Unruh的计算表明,该温度约为60纳开尔文。简而言之,随着加速度的增加,爱丽丝(Alice)陷入了温热的辐射浴中,其温度等于(以适当的单位)加速度除以以最终温度为特征。 Unruh的计算表明,该温度约为60纳开尔文。简而言之,随着加速度的增加,爱丽丝(Alice)陷入了温热的辐射浴中,其温度等于(以适当的单位)加速度除以以最终温度为特征。 Unruh的计算表明,该温度约为60纳开尔文。简而言之,随着加速度的增加,爱丽丝(Alice)陷入了温热的辐射浴中,其温度等于(以适当的单位)加速度除以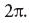
. 7.1。 , a . , , t = 0. , t = 0 . , ‑.
安鲁(Unruh)的计算很奇怪,尽管它们从头到尾都指的是空白空间,但却与李尔王(King Lear)的名言“无所不能”相矛盾。空的空间怎么会如此复杂?微粒从哪里来?事实是,根据量子理论,空的空间绝不是空的。在这里和那里,短暂的激发(称为虚粒子)不断出现和消失,这些激发的能量可以为正也可以为负。一个遥远的未来的观察者(我们称她为Carol),能够看到几乎所有的空白空间,可以确认其中没有永久存在的粒子。此外,在爱丽丝可以观察到的那段时空中,存在具有正能量的粒子,由于量子纠缠,它在时空的不可观测部分与等号和相反号的能量激发有关。整个空时空的全部真相对卡罗尔都是开放的,这个真相是没有粒子。但是,爱丽丝的经历告诉她,这里有微粒!, , , — , , . «» , «», , , . 2, , , , . , , . , , ? , . , ? , , , . , , .