🍐 ⬛️ 🏦 混沌的信息熵 🔟 🕴🏾 💩

引言

在Habr上有很多出版物都考虑了熵的概念，这里只是其中的一小部分[1÷5]。这些出版物受到了读者的积极欢迎，并引起了极大的兴趣。给出出版物[1]的作者给出的熵的定义就足够了：“熵是您不了解系统的多少信息。” 关于Habr的混沌现象的出版物也足够[6-9]。但是，两组出版物都没有考虑熵和混沌的关系。

这是由于以下事实：不同的知识领域可以区分不同类型的混乱度量：

信息性
热力学
差异
文化的。

还描述了混乱措施，并考虑到其特殊性，即使在这些区域之一中也相当困难。

为了尽可能简化任务，我决定以点映射的形式以及这些区域的熵系数图中的从有序到无序通行区域的相似性示例为例，考虑信息熵与混沌之间的关系。

通过在猫底下看，您将会学到什么。

从秩序到混乱的转变机制

对真实系统和各种模型中从有序过渡到混沌的机制进行了分析，发现了向混沌过渡的场景相对较少的通用性。可以用分叉图的形式表示向混沌的过渡（术语“分叉”用于表示系统随着行为的新模式的出现而进行的定性重排）。

系统进入不可预测的模式是由一系列接连的分叉来描述的。分叉的级联依次导致在两个解决方案之间进行选择，然后在四个解决方案之间进行选择，依此类推，系统开始以一种混乱的湍流模式振荡，将可能值的数量顺序加倍。

我们考虑了点映射中周期倍增的分叉和混沌的出现。显示是一项功能，用于显示系统参数的以下值与先前值的依赖关系：

（ ） （ ）

$x_ {n + 1} = f（x_ {n}）= \ lambda x_ {n}（1-x_ {n}）$

还考虑第二个常用功能：

（ ） （ ）

$x_ {n + 1} = f（x_ {n}）= \ lambda \ cdot x_ {n} \ cdot（1-x_ {n} ^ {2}）$

使用点映射，对象的研究不是连续的，而是离散的时间 。过渡到显示器后，正在研究的系统的尺寸可能会减小。

当更改外部参数\ lambda时，点映射会表现出相当复杂的行为，在足够大的\ lambda的情况下会变得混乱。混沌是相空间中轨迹的非常快速的后退。

分叉是对电影的定性重组。发生分叉的控制参数的值称为临界值或分叉值。

要构建图，我们将使用以下两个清单：

1号对于功能：

（ ） （ ）

$x_ {n + 1} = f（x_ {n}）= \ lambda x_ {n}（1-x_ {n}）$

程序清单

# -*- coding: utf8 -*- import matplotlib.pyplot as plt from numpy import * def f(a,x0): x1=(a-1)/a#     def ff(x):#  return a*x*(1-x) def fl(x): return x x=x0;y=0;Y=[];X=[] for i in arange(1,1000,1): X.append(x) Y.append(y) y=ff(x) X.append(x) Y.append(y) x=y plt.title('   \n\ $x_{n+1}=\lambda \cdot x_{n}\cdot (1-x_{n})$  $\lambda$ =%s  x0=%s '%(a,x0)) plt.plot(X,Y,'r') x1=arange(0,1,0.001) y1=[ff(x) for x in x1] y2=[fl(x) for x in x1] plt.plot(x1,y1,'b') plt.plot(x1,y2,'g') plt.grid(True) plt.show()

2号。为了功能

（ ） （ ）

$x_ {n + 1} = f（x_ {n}）= \ lambda \ cdot x_ {n} \ cdot（1-x_ {n} ^ {2}）$

程序清单

 # -*- coding: utf8 -*- import matplotlib.pyplot as plt from numpy import * def f(a,x0): x1=((a-1)/a)**0.5 def ff(x):#  return a*x*(1-x**2) def fl(x): return x x=x0;y=0;Y=[];X=[] for i in arange(1,1000,1): X.append(x) Y.append(y) y=ff(x) X.append(x) Y.append(y) x=y plt.title('   \n\ $x_{n+1}=\lambda \cdot x_{n}\cdot (1-x_{n}^{2})$  $\lambda$ =%s  x0=%s '%(a,x0)) plt.plot(X,Y,'r') x1=arange(0,1,0.001) y1=[ff(x) for x in x1] y2=[fl(x) for x in x1] plt.plot(x1,y1,'b') plt.plot(x1,y2,'g') plt.grid(True) plt.show()

评估逻辑功能性质对临界值的影响

$\ lambda$ 考虑具有功能的图

（ ） （ ）

$x_ {n + 1} = f（x_ {n}）= \ lambda x_ {n}（1-x_ {n}）$ 为此，我们将使用清单1：

对于0 <\ lambda <1对于

$\ lambda = $ 0.9$ 并且x0 = 0.47我们得到如下图：

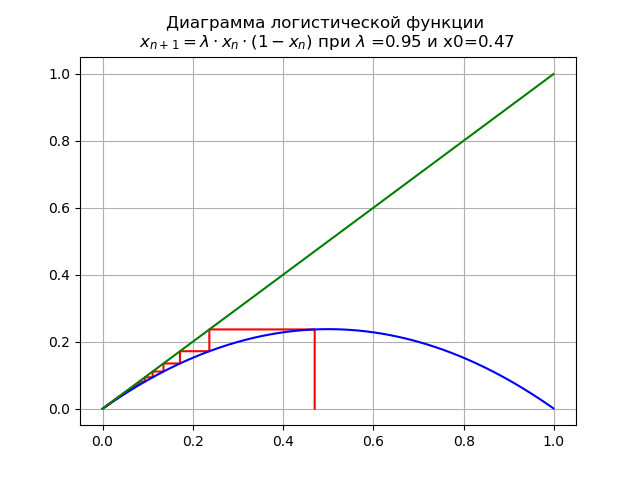
在这种情况下，地图只有一个固定点

$x ^ {*} = 0$
这是可持续的。

在

$1 <\ lambda <3$ 为

$\ lambda = $ 2.$ x0 = 0.7我们得到图：

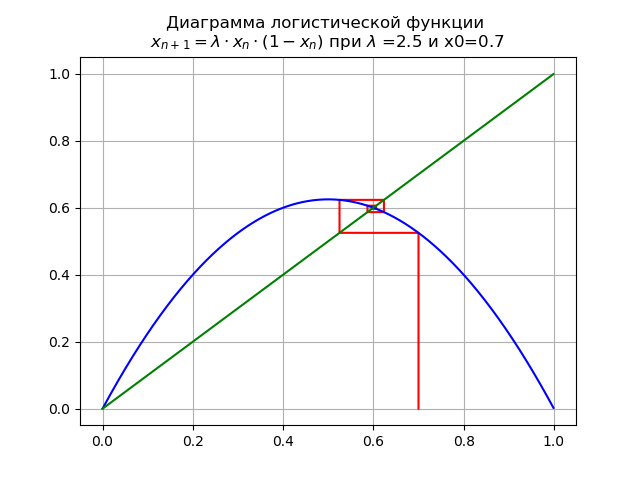
在段[0，1]上，出现另一个固定不动点

$x_ {1} ^ {*} = 1-1 / \ lambda$

在

$1 <\ lambda <3$ 为

$\ lambda = $ 2.$ x0 = 0.01，我们得到如下图：

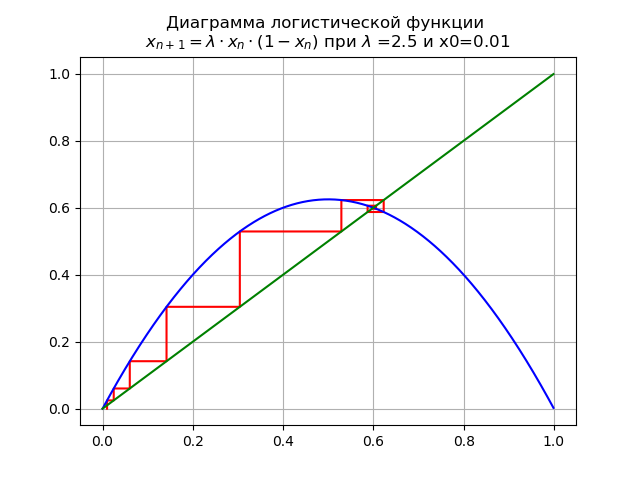
定点

$x ^ {*} = 0$ 失去稳定性。

在

$3 <\ lambda <3.45$ 为

$\ lambda = $ 3.4$ x0 = 0.7，我们得到如下图：

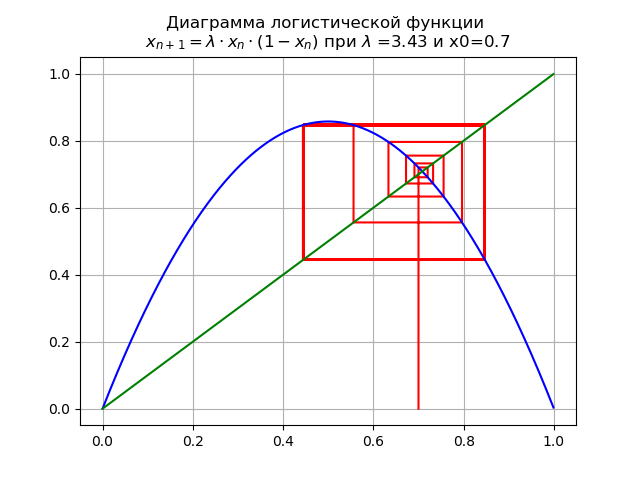
映射分叉：不动点

$x_ {1} ^ {*}$ 变得不稳定，而是出现一个双循环。

在

$3.45 <\ lambda <4.0$ 为

$\ lambda = $ 3.5$
x0 = 0.2我们得到如下图：

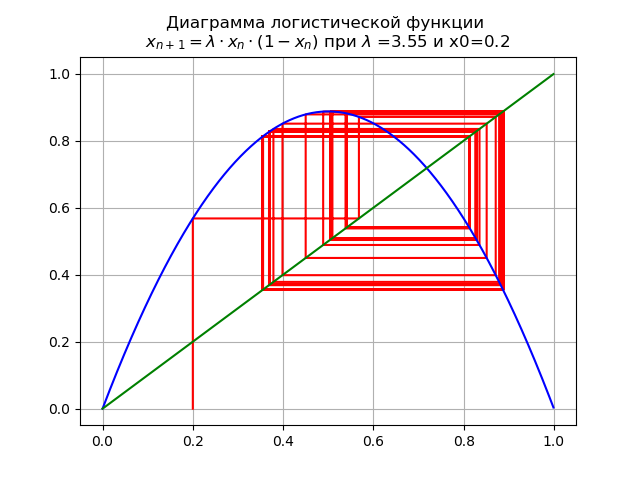
传递参数时

$\ lambda$ 通过价值

$\ lambda = 3.45$ ，则2倍循环变为4倍甚至更高。

以最终价值

$\ lambda = 4$ 系统的所有可能订单都有不稳定的周期：

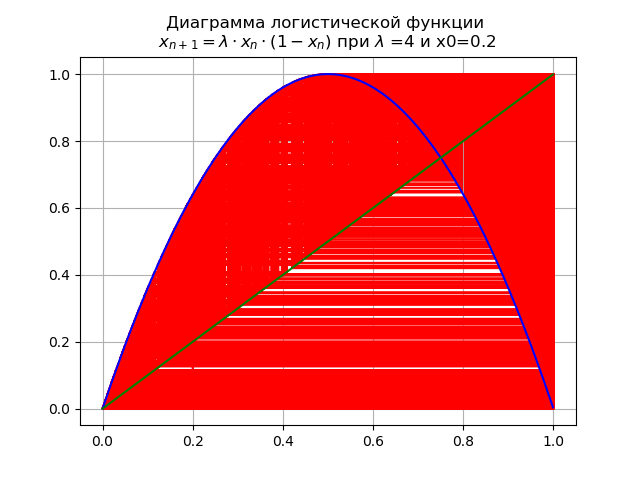
评估逻辑功能性质对临界值的影响

$\ lambda$ 考虑具有功能的图

（ ） （ ）

$x_ {n + 1} = f（x_ {n}）= \ lambda \ cdot x_ {n} \ cdot（1-x_ {n} ^ {2}）$ ，为此，我们将使用清单2。

在

$0 <\ lambda <= 1.0$ 为

$\ lambda = 0.5$ 并且x0 = 0.2：

映射具有单个固定点

$x ^ {*} = 0$ 这是可持续的。

在

$1 <\ lambda <= 1.998 ...$ 为

$\ lambda = $ 1.$ 并且x0 = 0.55：

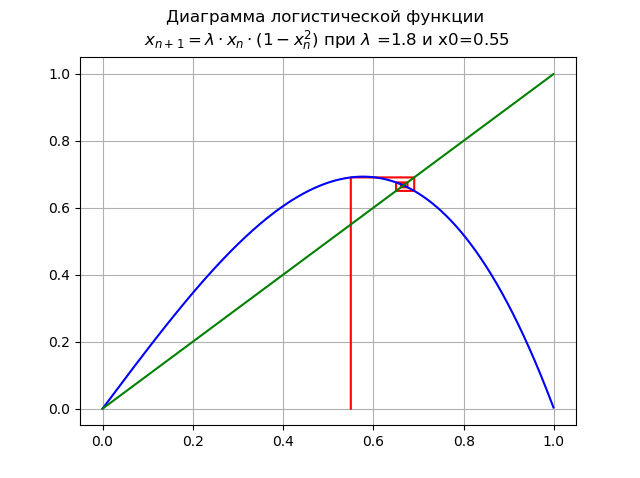
点数

$x ^ {*} = 0$ 失去稳定性，出现新的稳定点

$x_ {1} ^ {*}$

在

$1.99 <\ lambda <= 2.235 ...$ 为

$\ lambda = $ 2.$ 并且x0 = 0.2：

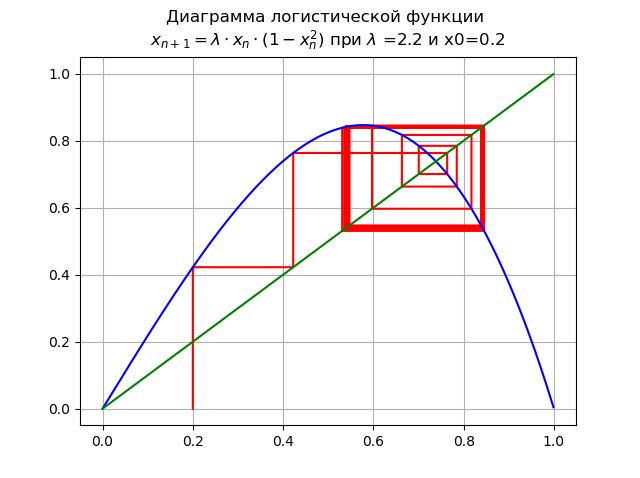
周期加倍发生分叉，出现2倍循环。进一步增加

$\ lambda$ 导致周期倍增分叉的级联。

在

$2,235 <\ lambda 2.5980 ...$ 为

$\ lambda = 2.287$ 并且x0 = 0.2：

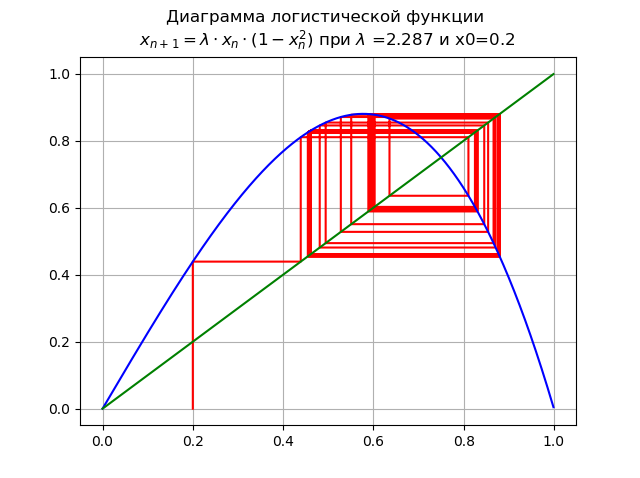
增加

$\ lambda$ 导致级联倍增分叉的级联。

在

$\ lambda = 2.59$ 系统在所有可能的周期内都有不稳定的周期：

如图所示，随着逻辑函数顺序的增加，变化范围

$\ lambda$ 逐渐减少。

使用图，我们在设置值的同时跟踪了从顺序到混乱的路径

$\ lambda$ 用于不同的物流功能。仍然需要回答这个问题：如何衡量混乱？本文开头列出的某些类型的混乱的答案是已知的
-熵是对混沌的一种度量。这个答案可以完全归因于信息混乱，但是，这里应用了什么熵以及如何与已经考虑过的数值进行比较

$\ lambda$ -我将在本文的下一部分中尝试回答这个问题。

信息熵和熵系数

我们将考虑独立随机事件的信息二进制熵。

$x$ ç

$n$ 概率分布的可能状态

$p_ {i}（i = 1，..，n）$ 。信息二进制熵由以下公式计算：

$H（x）=-\ sum_ {i = 1} ^ {n} p_ {i} \ cdot log_ {2}（p_ {i}）$

此值也称为消息的平均熵。价值

$H_ {i} =-日志{2}（p_ {i}）$ 称为私有熵，仅表征第i个状态。在一般情况下，熵定义的对数底数可以大于1；反之亦然。他的选择决定了熵的度量单位。

我们将使用十进制对数，其中熵和信息以位为单位。例如当使用变量时，将正确计算以位为单位的信息量

$X$ 和

$\三角洲$ 不论在哪个位置，但总是以相同的单位被替换为相应的熵表达式。确实：

$q = H（x）-H（\ Delta）= log_ {10} \左（X_ {2} -X_ {1} \ right）-log_ {10}（2 \ Delta）= log_ {10}（\ frac {X_ {2} -X_ {1}} {2 \ Delta}）$

X和

$\三角洲$ 必须使用相同的单位。

从实验数据中随机变量的熵值的估计值可以从直方图中根据以下关系找到：

$\ Delta_ {e} = \ frac {1} {2} e ^ {H（x）} = \ frac {d} {2} \ prod_ {i = 1} ^ {m}（\ frac {n} { n_ {i}}）^ {\ frac {n_ {i}} {n}} = \ frac {dn} {2} 10 ^ {-\ frac {1} {n}} \ sum_ {i = 1} ^ {m} n_ {i} log_ {10}（n_ {i}）$

其中：

$d$ –直方图每一列的宽度；

$m$ -列数；

$n$ -数据总量；

$n_ {i}$ -中的数据量

$我$ 该列。

熵系数由以下比率确定：

$k_ {e} = \ frac {\ Delta_ {e}} {\ sigma}$

其中：

$\ sigma$ -标准偏差。

信息熵衡量混乱

为了使用熵系数分析信息混乱现象，我们首先为函数创建一个分支图

$x_ {n + 1} = f（x_ {n}）= \ lambda x_ {n}（1-x_ {n}）$ 应用在直方图构建过程中获得的过渡区域：

分支图

 import matplotlib.pyplot as plt import matplotlib.pyplot as plt from numpy import* N=1000 y=[] y.append(0.5) for r in arange(3.58,3.9,0.0001): for n in arange(1,N,1): y.append(round(r*y[n-1]*(1-y[n-1]),4)) y=y[N-250:N] x=[r ]*250 plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1) plt.figure(1) plt.title("   3,6<= $\lambda$ <=3,9") plt.xlabel("r") plt.ylabel("$\lambda$ ") plt.axvline(x=3.63,color='black',linestyle='--') plt.axvline(x=3.74,color='black',linestyle='--') plt.axvline(x=3.83,color='black',linestyle='--') plt.axvline(x=3.9,color='black',linestyle='--') plt.show()

我们得到：

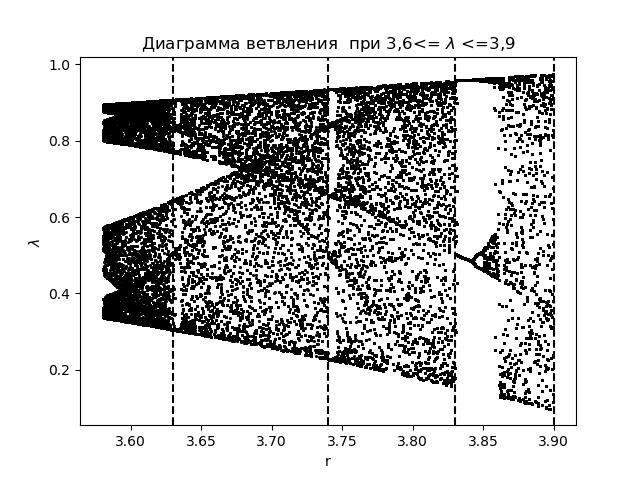
我们绘制相同区域的熵系数

$\ lambda$ ：

熵系数图

 import matplotlib.pyplot as plt from numpy import* data_k=[] m='auto' for p in arange(3.58,3.9,0.0001): q=[round(p,2)] M=zeros([1001,1]) for j in arange(0,1,1): M[0,j]=0.5 for j in arange(0,1,1): for i in arange(1,1001,1): M[i,j]=q[j]*M[i-1,j]*(1-M[i-1,j]) a=[] for i in arange(0,1001,1): a.append(M[i,0]) n=len(a) z=histogram(a, bins=m) if type(m) is str: m=len(z[0]) y=z[0] d=z[1][1]-z[1][0] h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n) ke=round(h/std(a),3) data_k.append(ke) plt.title("  ke  3,6<= $\lambda$ <=3,9") plt.plot(arange(3.58,3.9,0.0001),data_k) plt.xlabel("$\lambda$ ") plt.ylabel("ke") plt.axvline(x=3.63,color='black',linestyle='--') plt.axvline(x=3.74,color='black',linestyle='--') plt.axvline(x=3.83,color='black',linestyle='--') plt.axvline(x=3.9,color='black',linestyle='--') plt.grid() plt.show()

我们得到：

比较图和图，我们可以看到图和图上区域的相同显示，该函数的熵系数

$x_ {n + 1} = f（x_ {n}）= \ lambda x_ {n}（1-x_ {n}）$ 。

为了使用熵系数进一步分析信息混乱现象，我们为逻辑函数创建了一个分支图：

$x_ {n + 1} = f（x_ {n}）= \ lambda \ cdot x_ {n} \ cdot（1-x_ {n} ^ {2}）$ 过渡区域的应用：

分支图

 import matplotlib.pyplot as plt from numpy import* N=1000 y=[] y.append(0.5) for r in arange(2.25,2.56,0.0001): for n in arange(1,N,1): y.append(round(r*y[n-1]*(1-(y[n-1])**2),4)) y=y[N-250:N] x=[r ]*250 plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1) plt.figure(1) plt.title("   2.25<=$\lambda$ <=2.56") plt.xlabel("$\lambda$ ") plt.ylabel("y") plt.axvline(x=2.34,color='black',linestyle='--') plt.axvline(x=2.39,color='black',linestyle='--') plt.axvline(x=2.45,color='black',linestyle='--') plt.axvline(x=2.49,color='black',linestyle='--') plt.axvline(x=2.56,color='black',linestyle='--') plt.show()

我们得到：

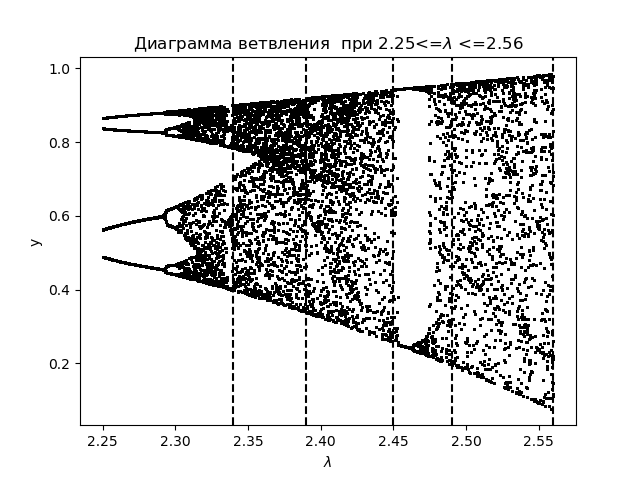
我们绘制相同区域的熵系数

$\ lambda$ ：

熵系数图

 import matplotlib.pyplot as plt from numpy import* data_k=[] m='auto' for p in arange(2.25,2.56,0.0001): q=[round(p,2)] M=zeros([1001,1]) for j in arange(0,1,1): M[0,j]=0.5 for j in arange(0,1,1): for i in arange(1,1001,1): M[i,j]=q[j]*M[i-1,j]*(1-(M[i-1,j])**2) a=[] for i in arange(0,1001,1): a.append(M[i,0]) n=len(a) z=histogram(a, bins=m) if type(m) is str: m=len(z[0]) y=z[0] d=z[1][1]-z[1][0] h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n) ke=round(h/std(a),3) data_k.append(ke) plt.figure(2) plt.title("  ke  2.25<= $\lambda$ <=2.56") plt.plot(arange(2.25,2.56,0.0001),data_k) plt.xlabel("$\lambda$ ") plt.ylabel("ke") plt.axvline(x=2.34,color='black',linestyle='--') plt.axvline(x=2.39,color='black',linestyle='--') plt.axvline(x=2.45,color='black',linestyle='--') plt.axvline(x=2.49,color='black',linestyle='--') plt.axvline(x=2.56,color='black',linestyle='--') plt.grid() plt.show()

我们得到：

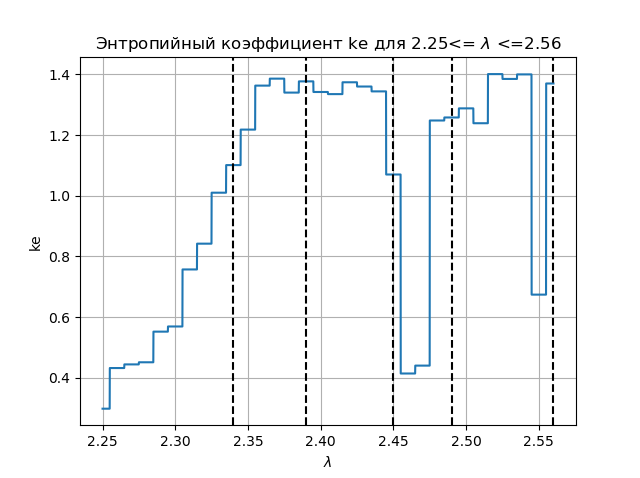
比较图和图，我们可以看到图和图上区域的相同显示，该函数的熵系数

$x_ {n + 1} = f（x_ {n}）= \ lambda \ cdot x_ {n} \ cdot（1-x_ {n} ^ {2}）$

结论：

本文解决了教育问题：信息熵是对混沌的一种度量，而Python肯定地给出了这个问题的答案。

混沌的信息熵

引言

从秩序到混乱的转变机制

信息熵和熵系数

信息熵衡量混乱

结论：

参考文献

More articles: