基于快速傅里叶变换（FFT）的平稳随机过程的光谱估计方法是众所周知的，并在工程实践中得到广泛使用。 它们的缺点尤其包括估计值的高分散性（低准确性），并且该过程的观察间隔不足，这通常在视觉上以功率谱密度（PSD）的强“缩进”图显示出来。 光谱估计的替代方法之一是自回归方法，在下面的示例中考虑了这一点，这在工程实践中鲜为人知。 在许多情况下，该方法相对容易获得更好的PSD估计值（图1），有时甚至可以获得有关正在研究的随机过程的更深入信息。
图1对“短”过程PSD的经典和自回归评估为了演示的目的，合成了一个离散时间信号（序列）x [i]。 使用ARMA模型（数字滤波器）对信号进行建模，以模拟机械系统的特性（1）-在参数为m = 1 kg，c = 100 N / m，k = 2的“单质量”振荡器中移动材料点x（t）。 5 kg / s，并通过力扰动-色散为1 N
2的高斯“白”（考虑离散）噪声f（t），时间间隔Δt= 0.12 s。
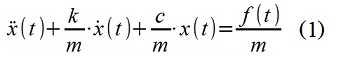
建立模型（2）。
此处早已考虑了构建模型的方法。
x [i]-0.6388·x [i-1] + 0.7408·x [i-2] = 0.009667·f [i-1] （2）
使用（2），合成了5万个样本的序列，为此，使用了众所周知软件环境的正态分布随机变量randn（）的生成器。
在完成对过程x [i]的模拟后，假定模型（2）的定量参数未知-仅可用于过程本身，并且在某种程度上，可以使用有关最一般术语的模型属性的信息进行研究。
使用韦尔奇（Welch）方法对50,000点序列进行光谱估计，片段大小等于256个样本，应用汉明窗和片段的60％重叠。 基于序列长度约为200个非重叠片段的事实，这种估计的标准偏差可以大致估计为7％。
此外，假设在实验的真实条件下，可以使用更短的序列进行研究，则仅对该信号的前500个样本进行研究。
使用相同参数的Welch方法获得估计值。 这种估计的标准偏差约为70％；该图的“粗糙度”非常明显（图2）。
图2.用经典方法评估“长”和“短”过程的PSD基于我们知道SPM过程的函数（图形）的近似形式这一事实（例如，基于过程的已知物理性质-白噪声下的单质量振荡器，或通过评估可用更长实现时间的类似过程），我们决定评估使用二阶自回归模型（AR（2）或= ARMA（2.0））。
确定模型的顺序是非常重要的一点；顺序中的错误会导致估计结果中非常严重的错误。 有些方法尚未在此处考虑，仅基于正在分析的过程有助于确定模型的顺序。
使用众所周知的Yule-Walker方程对自回归过程进行模型参数的估计（稍作修改以略微简化脚本的结构）：
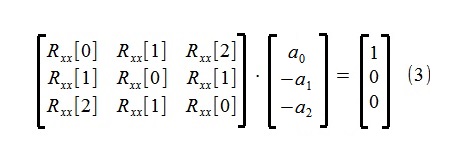
从等式可以看出，要确定参数，仅使用自回归序列Rxx [0]，Rxx [1]，Rxx [2]的前三个成员，这些序列是通过相关图方法从初始500点序列x [i]估计的〜4.5％。
（顺便说一句，很明显，a
1 ，a2
2等之前的“缺点”非常不方便。之所以出现，是因为在经济中主要是“预测性”地使用了ARMA模型，这是因为它们的早期“工程”来源否。我已经怀疑是否有必要在这里使用对AR系数的这种理解。）
实际上，（3）中的相关矩阵始终具有严格的对角线流行度。 Rxx [0] | > | Rxx [i] |，包括由于存在观察到的噪声而导致的，其处理没有困难（找到解决方案（3））。
（为澄清统计建模误差的大小问题，有趣的是，例如，与从50,000个样本获得的色散估计值相关的相关图= 2.4238e-04 m
2相比，从500个样本获得的估计值Rxx [0] = 2.2606e-04 m
2并通过Welch方法获得的PSD区域的积分对5万个样本进行估计（图2），= 2.4232e-04 m
2 ）
替换找到的估计值Rxx [i]后，我们得到：
确定以下模型参数
0 = 11325.9;
1 = 7090.1; a
2 = -8411.5； 从（3）可以看出，假设的传入白噪声的色散在此处设置为1，而不是将增益确定为
0 。 通过对一系列系数a
0 ，a
1 ，a
2进行傅立叶变换来构造PSD的自回归估计：
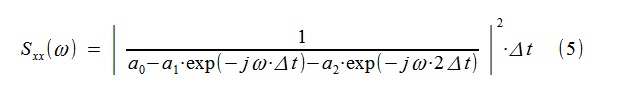
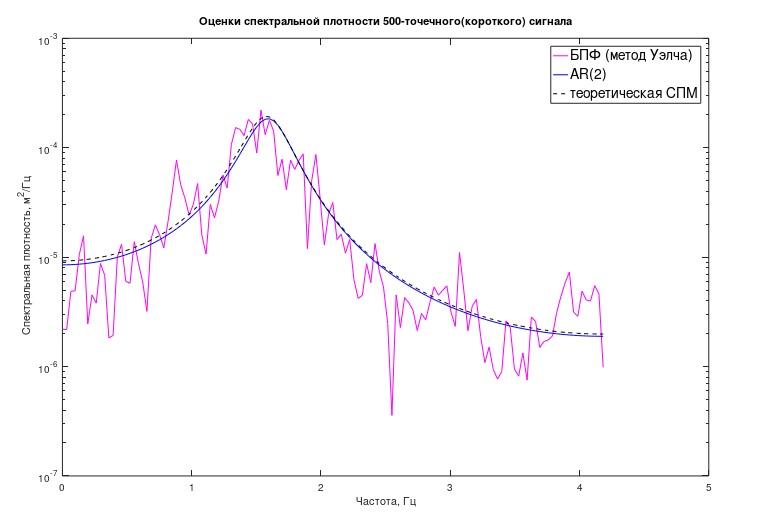图3对“短”过程PSD的古典和自回归评估同样，根据类似于（5）的表达式，较早地构建了PSD的“理论”进度表，当然只有那里的模型系数是不同的（与（2）不同）。
从图中可以看出，PSD的AR估计值非常接近理论上的预期值。 除了图表以外，还可以尝试评估过程和相关机械系统的某些分析特性。 在这种情况下，它们是模型的“极点”，在数值上表征了模型的“共振”峰的频率以及相关的“品质因数”。
从（5）中，我们找到使用拉普拉斯变换搜索模型传递函数的不连续性的关系（用λ=-ε+jω代替jω）：
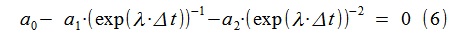
对于获得的AR模型，以这种方式计算λ1,2 = -1.5427±j·10.1514，这与用于生成过程的原始模型非常接近
λ1.2theor = -1.2500±j·9.9216（即，共振峰的位置分别为1.615 Hz（理论上）和1.579 Hz（确定））。
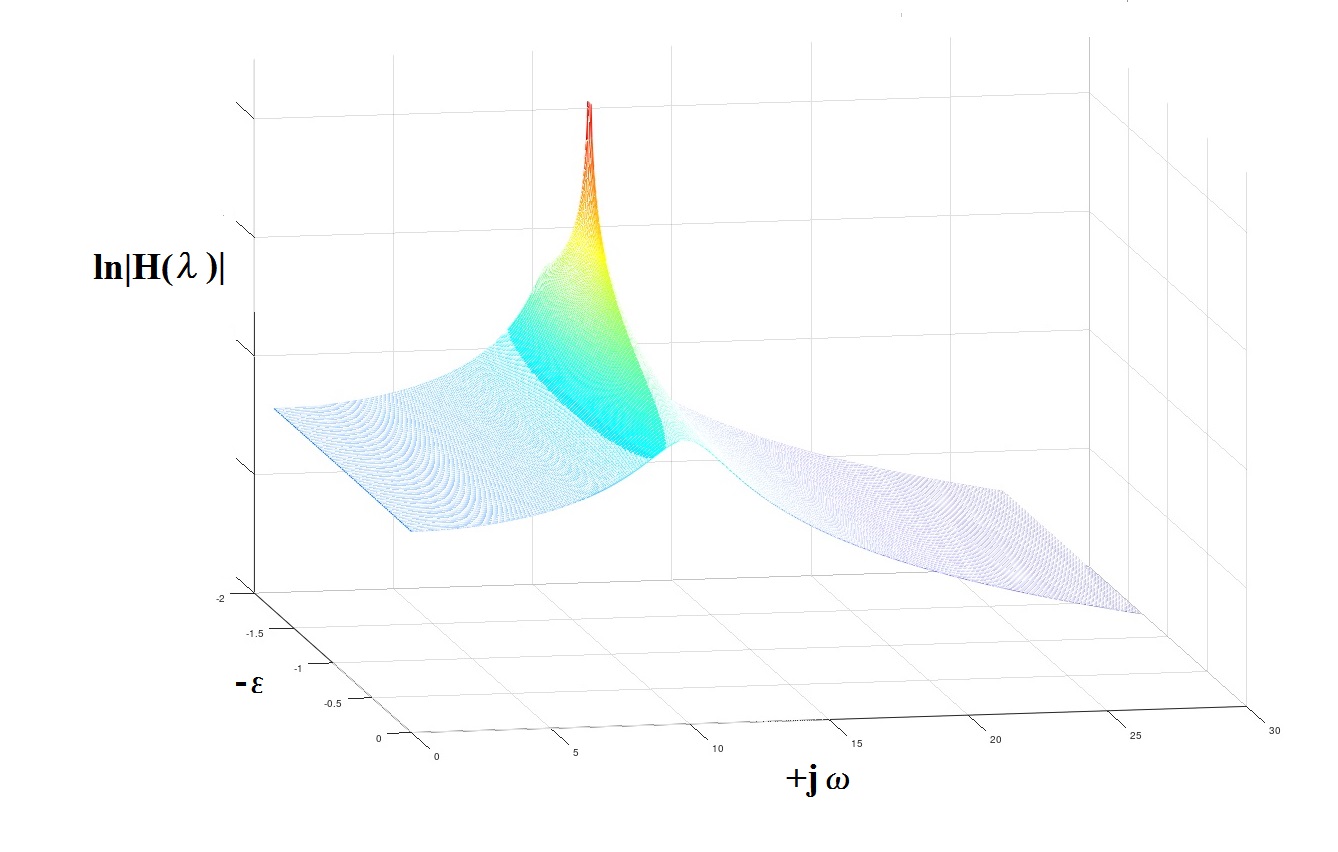图4关于“极点”的概念结论中的一些评论和建议。
- 从获得带有严重误差的PSD估计值的风险的角度来看，AR模型的“过大”（太大）阶数通常要危险得多而不是不足。
- 通常，AR建模可以相当准确地确定谐振频率jωk，而不太准确地确定相应“峰”-εk的宽度
- ARMA-该模型可能比AR模型小得多（大小），据许多消息来源称，AR模型似乎旨在提高模型的准确性。 但是，评估模型的MA部分要困难得多，通常可能包括获得大阶AR模型以将其进一步转换为MA部分的第一步。 关于这些来源，对于使用精确的AR模型进行频谱估计（尽管是更高阶的）的可取性，也表达了另一种观点。
- 对于非常短的以及非平稳的过程，协方差矩阵通常用于（3）中，而不是自相关函数的估计矩阵。
- 对于自回归光谱估计问题的详细研究，S.L。 Marple毫升。 “数字频谱分析及其应用”，M.，Mir，1990年