关于山峰附近

“在您理解这一点之前，这似乎是一个奇迹。 但是在那之后没有什么特别的。”

不，不是关于山脉，而是关于计数。 在数学中，存在着每个人都可以理解其提法的问题，但是解决方案并不简单，而且没有特殊的准备就很难解释。 这些问题之一可以简述如下： 如何正确计算有向图中的距离？ 这个有点抽象的问题可以简化为非常具体的激励任务。 它适合一张图片：

1.问题陈述。 我住在一个，但你住在另一个。

将一个小镇（例如，通过河流划分，尽管在山峰的峡谷中更合适）分为两个区（部分） $$和 $$$B$ 。 区域之间的通信沿着一条道路（桥）进行，该道路有两条车道：到 $$到 $$$B$ 反之亦然。 关于人口增长，提出了增加公路通行能力的问题。 像往常一样，钱仅够一个方向上的一个车道。 显然，即使只有一个车道也会使区域更靠近，但是问题是究竟有多少？ 您是一位城市疯狂的数学家，邀请您来获得合理答案的是您。

如果在一个方向上再建一条带，则这些区域之间的距离有多近？

高级措辞

代替Konigsberg桥，可以使用稍微更严格的图论语言。 因此，有一个有两个顶点（节点）的有向图 $$和 $$$B$ 。 正向和反向的连接大小（电导率，带宽）最初相等。 问题是，如果其中一个方向的电导率加倍，那么节点之间的距离会改变多少？

是的，如果您是真正的数学家焊机 ，则可以为任何直接值和反馈值提供（并证明）解决方案。 理想情况下，对于具有任意数量的节点和链接的图。

亲密和醉酒徘徊

显然，区域之间通常的（公里）距离并不取决于道路的存在与否。 因此，它不适合这里-我们需要依靠沟通。 连接的区域越多-距离越近-单位时间内到达另一个区域的居民越多。

为了评估无向图的节点之间的接近度，可以使用所谓的电阻距离 。 之前，我们已经在几篇文章中描述了在habr上此距离的属性。

当涉及到电网时，电阻距离等效于有效电阻的概念。 因此，用电子语言，该问题可以表述如下。 在两个节点之间，逆时针连接了两个电导率相等的二极管。 如果添加另一个二极管，这些点之间的电阻将如何变化？ （如果电子语言失败，我表示歉意，我在这里写了废话）。

同样，对于醉酒的随机游走的概率，可以用马尔可夫语言来解释有效的抵抗力（对于那些希望深入研究这一主题的人-谷歌“随机游走和电力网络”）。

电阻距离是平方的，-对应于线性距离的平方。 二次距离也称为四边形 。 但是由于此问题中未使用其他（线性）距离，因此此处不需要术语四边形。 （即使没有，也有足够的鸟舌）。

通常，术语“电阻距离”看起来也不好。 他暗示我们正在谈论某种科学未知的异常距离。 实际上，电阻距离是通常的欧几里得距离 。 但是在仿射空间。 我们将进一步使用此功能。

到底是什么问题？

如果我们知道什么是“电阻距离”，那么为什么不能为给定的图形“仅取并计算”？

嗯 原则上，容易。 如果我们谈论的是无向图。 如果城市在两个方向上都建了条状地带，那么电阻距离将减少一半。 由于电阻与电导率成反比，因此电导率（吞吐量）增加了一倍。 如果我在每个方向上添加两个波段，则距离将减少3倍。 这里的一切都很琐碎。 （也许，这里的人已经可以猜出解决方案的一般形式。我们可以做得更进一步）。

当相对关系不相等时，一切都会变得复杂。 而且非常严厉。

没有一种简单的法律公认的方法可以确定方向图中的峰值附近（电阻距离）。

（这是我的论点-也许有人可以说服我）。 “不”（这里是指它不在教科书，维基百科和头脑中）（更确切地说，来自不同作者的方法有很多，需要不同的假设和定义）。 有一种方法（尽管不是那么简单）。 在本文中，我们只是对其进行描述。

如果我们谈论的是有向图（非交换度量，我表示歉意），那么在确定有向连接时距离的确定非常必要。 你可以说说到 $$之前 $$$B$ ，但您可以从 $$$B$ 之前 $$。 而且最有可能这些距离并不总是相等的。 我们在这个问题上谈论的距离是多少？

欧氏距离规则

我们将出现并深呼吸。 我们已经提到电阻距离是通常的欧几里得。 这意味着其定义可以简化为欧几里得距离的定义，作为两个元素之差的范数：

$$$S（A，B）= | A-B | ^ 2 =（A-B）^ 2 =（A-B）\ cdot（A-B）= S（B，A）\四边形（1）$

此定义不取决于元素的顺序-这是元素的交换距离，接近度（更确切地说是距离）。 表达式中的点表示标量积运算（度量空间）。 因此，可以公开表达式（1）：

$$$S（A，B）= S（B，A）= A ^ 2 + B ^ 2-A \ cdot B-B \ cdot A \ quad（2）$

在这里 $$$A ^ 2 = A \ cdot A$ ， $$$B ^ 2 = B \ cdot B$ -要素规范。 对于图形，元素的范数通常为零。 在最初的问题中，没有任何关于规范的说明，因此您可以将它们设为零（关于仿射空间中元素的规范的含义更多。 在此处 ，甚至更多详细信息， 在此处 ）。 然后，所需距离的表达式采用以下形式：

$$$S（A，B）=-（A \ cdot B + B \ cdot A）= s_ {AB} + s_ {BA} \ quad（3）$

根据表达式（3），解决问题所需要的只是在有向图中找到元素（节点）的标量积（这很容易说出来，但是如何做到这一点？）。

在此过程中，公式（3）表明我们对元素之间接近程度的一般（可交换）度量 $$和 $$$B$ 是两个有向距离的和：

$$$s_ {AB} =-A \ cdot B$ -与的方向距离 $$之前 $$$B$ ，
$$$s_ {BA} =-B \ cdot A$ -与的方向距离 $$$B$ 之前 $$。

2.决定。 在沙丘上漫长的路

隆隆声消退了。 乐趣已经结束。 接下来是对用于计算有向图的节点之间的标量积的方法的本质的描述的沉闷细节。 这是我不知道该如何“用手指简单地说”的部分。 但这是本文中最重要的内容。 值得浪费时间的东西。

推理的大致思路如下。 我们小心翼翼地在没有其他新假设的情况下将对称空间的度量的已知属性转换为非对称空间的度量。 所需要做的就是考虑仿射空间中度量的特殊性。

任何连接的图（无论是否有向）都定义了一个仿射度量空间。 这种空间在对称（交换）执行中的某些特性在（已混乱地）描述的系列文章中进行了描述，或更精确地在所提及的longrid中进行了详细描述。 不要急于切换-在下面我们给出（尽管通过绕口令）主要挤压。

仿射度量空间（无向图）

重要的是。 知名第一。

1.空间的亲和力意味着空间中向量和元素的概念是不同的。 向量是元素的区别。 如果在空间中定义度量，则此看似微不足道的功能会导致重大后果。

2.空间由包含元素的基础定义。 图的顶点是空间的基础。 图中的关系确定其度量标准属性。

3.图的连通性特征是邻接矩阵 。 但是对于度量（和其他）属性，图的拉普拉斯算子（基尔霍夫矩阵）更为重要 $$$L$ 。

4.图的拉普拉斯算子是几乎度量的张量。 “几乎”-此处表示不完整。 拉普拉斯算子是简并矩阵，因此不可逆。 标准度量张量是完全可逆的。

现在鲜为人知。

5.度量仿射空间中元素和向量之间的差异导致其中存在空向量 $$$\ mathbb z$ 。 在交换（对称）空间中具有零向量的元素的标量积等于1（在非交换空间中，它取决于乘法方向）。 没有零向量，图空间将不完整！ 这很重要。

6.基础的正交中心相对于零向量为对偶。 $$$Z$ 。 这种元素与基础的所有其他元素（除零向量外）正交。 回想一下元素的正交性意味着它们的标量积为零。 三角形的正交中心是外接圆 。 是的，在一个完整的仿射空间中，具有非零范数的元素不是点，而是n维球体。

7.图的拉普拉斯算子以及正交中心的坐标变得完整（完整的度量张量）。 换句话说，完整的拉普拉斯算子 $$$Lm$ 是普通伯爵 $$$L$ 但以正交中心的重心坐标为边界。

8.完整的拉普拉斯算子的反演允许获得完整的格拉姆算子 $$$Gm$ -基础元素的标量积矩阵（在我们的情况下为图形的顶点）。 此gramian也是空间的完整度量张量。

9.完整gramian的帧是单位元组（基本元素和零向量的标量积）。 在角落-零，这是零向量本身的范数。
著名的Cayley-Menger矩阵几乎是规则的Gramian。

结果，我们得出结论，根据权利要求8，确定图的节点之间的标量积（以及因此的距离）的问题减少到确定基的初始度量张量 $$$Gm$ 。

我们需要一种构造完整的gramian图的方法 $$$Gm$ 对于给定的（不完整的）拉普拉斯算子 $$$L$ 。

在对称键的情况下，从拉普拉斯算式（反之亦然）构造完整的格拉姆式算式不会造成任何特殊困难。 在这种情况下，基数元素和零向量的标量积是可交换的-它们不取决于乘法的顺序：

$$$\ mathbb z \ cdot A = A \ cdot \ mathbb z = 1$

对于有向图（非交换空间），问题很复杂。 仅仅是因为有向图中的可能连接的数量增加了一倍。

非交换仿射空间（有向图）

关于有向图的拉普拉斯算子的性质，我们也已经在Habr上写过 。 他们讲述了如何利用拉普拉斯算子的潜力对物体进行排名。 就基数而言，拉普拉斯算子的势是零向量（拉普拉斯算子的零化子）的对偶坐标。

在本文中，我们对度量标准属性感兴趣。 如果图形是有向的，则其顶点之间的标量积取决于顺序：

$$$A \ cdot B \ ne B \ cdot A$

这意味着有向图中的双坐标被拆分（分为左和右）。 零向量的标量乘积与基础元素（与gramian相邻）的标量值也取决于因子的顺序。 因此，与可交换空间相反，此处零向量的对偶坐标的一半是未知的，必须确定。

$$$\ mathbb z \ cdot A \ ne A \ cdot \ mathbb z$

但是，有许多已知数量。

首先，拉普拉斯人本人是众所周知的。 另外，已知行的总和为零（在一般情况下，这是可选要求，但对于有向图的拉普拉斯算子通常是这种情况）。 同样重要的是，元素的重心坐标必须唯一，因为它们与空间度量无关。 也就是说，图的拉普拉斯算子的边界对于有向图和无向图都是对称的（我没有立即认识到这一点）。 最后，我们知道了基础元素的范数（通常在图中它们等于零）。

它仍然可以替代拉普拉斯和格拉姆系的所有已知和未知：

$$$Lm \ Gm =我$

在这里 $$$我$ 是一个单位矩阵。 在这种身份下，从不完整的拉普拉斯算子到完整的拉普拉斯算子的转变的含义。

闭嘴相信

让我们从言传身行。 这就是拉普拉斯人的模样 $$$L$ 对于两个节点的图：

$$$L = \开始{bmatrix} c_1和-c_1 \\ c_2＆-c_2 \结束{bmatrix}$

为简单起见，我们用数字指定了关系： $$$c_1 = c_ {AB}，c_2 = c_ {BA}$ 。 假定债券的价值是已知的-通过它们我们将表达所有其他数量。

全拉普拉斯式 $$$Lm$ 包括正交中心的坐标 $$$[rz，az，bz]$ ：

$$$Lm = \开始{bmatrix} rz＆az＆bz \\ az＆c_1＆-c_1 \\ bz＆c_2＆-c_2 \结束{bmatrix}$

在这里 $$$rz$ -正交中心的范数（在对称情况下被解释为半径的平方）， $$$az$ 和 $$$bz$ -基于此的原心分解系数 $$$A，B$ （重心重量）。

全文法 $$$Gm$ 看起来像这样：

$$$Gm = \开始{bmatrix} 0＆za＆zb \\ 1＆0＆g_1 \\ 1＆g_2＆0 \结束{bmatrix}$

这是元组 $$$[za，zb]$ 和 $$$[1，1]$ 反映空向量的对偶坐标。 这些坐标是拉普拉斯算子的ni 灭者 （当与拉普拉斯算子相乘时，它们给出零向量-请勿与零向量相混淆！）。

要解决此问题，我们需要找到gramian值的总和： $$$-（g_1 + g_2）$ 。

我们考虑未知数： $$$rz，az，bz，za，zb，g_1，g_2$ -仅7个（是的，是的-要找出一个不幸距离的值，我们需要再计算七个附加值）。 入口处有两个著名的连接- $$$c_1$ 和 $$$c_2$ 。 身分识别 $$$Lm \ Gm =我$ 将给出9个方程。 总计7 + 2 = 9，-一切收敛（令人惊讶）。 只需简单地求解方程组就可以了。

对于两个节点的图，解决方案（所有未知数）可以以显式形式表示。 我们对我们感兴趣的数量给出有限的表达式。 我们介绍了一般几何连通性的概念-这是正交中心范数的倒数 $$$gc = 1 / rz$ 。 其尺寸与图形链接的尺寸一致。 对于两个节点（和两个连接）的图形，几何连接具有一个很好的表达式：

$$$gc = 1 / rz =（\ sqrt {c_1} + \ sqrt {c_2}）^ 2$

通过这种连接，人们可以表达节点的标量积：

$$$g_1 = -gc \ sqrt {c_2}，\ quad g_2 = -gc \ sqrt {c_1}$

您可以翻译标量产品 $$$g$ 在定向距离 $$$s$ （3）：

$$$s_ {BA} = gc \ sqrt {c_ {AB}}; \ quad s_ {BA} = gc \ sqrt {c_ {AB}}$

节点之间的所需交换距离由总和确定：

$$$S（A，B）= s_ {BA} + s_ {AB} = 1 / \ sqrt {c_ {AB} c_ {BA}} \ quad（4）$

奶奶到了

终于 表达式（4）-这是所需的公式。

两个节点的图的顶点之间的距离与反向链接的乘积的平方根成反比。

您可以使用其他无用的公式加载学校教科书。

如果连接相等，则结果与无向图中的电阻距离重合：

$$$S_ {c，c}（A，B）= 1 / c \四边形（4.1）$

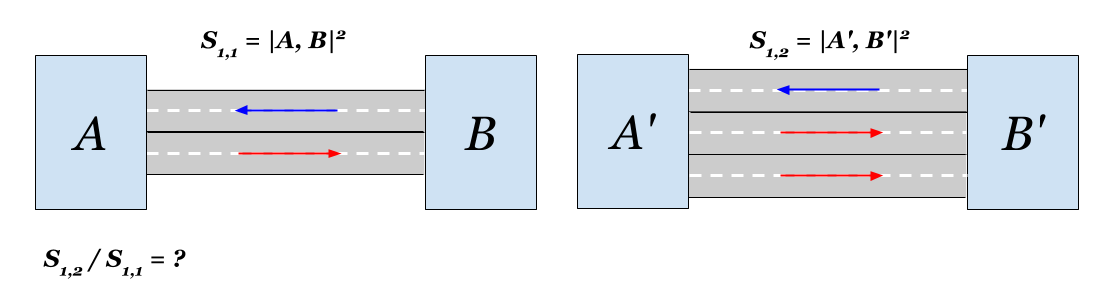
我们将计算镇上的东西。 如果您铺设第二条车道，则一个方向的通信将加倍。 因此，新距离 $$$S_ {1，2}（A，B）$ 可以用原文表达：

$$$S_ {1，2}（A，B）= 1 / \ sqrt {2 c_ {AB} c_ {BA}} = 1 / \ sqrt {2} S_ {1，1}（A，B）$

区域之间的距离将减小 $$$\ sqrt {2}$ 次。 很明显吧？

事实证明，就距离而言，在每侧的每条两车道道路上增加一条车道等同于在一侧增加3条车道。 在两种情况下，欧几里得距离都将增加一倍。 有趣



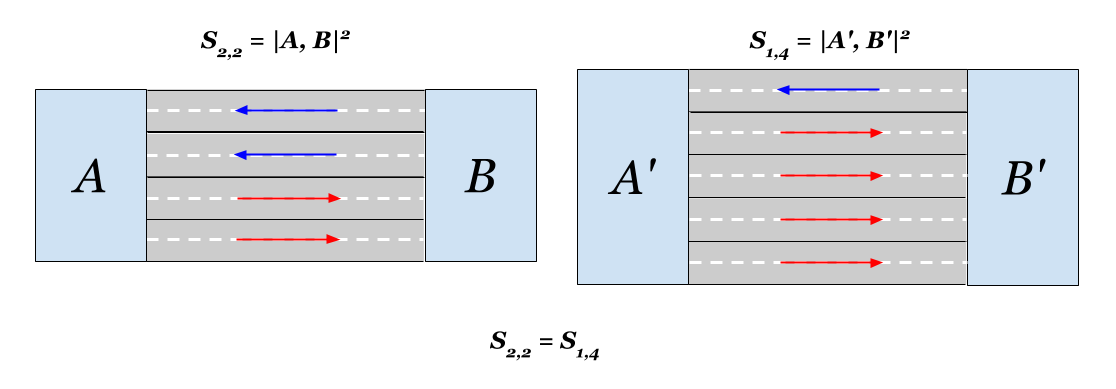
仅此而已。 谢谢您的关注）。