在证明就是一切的数学中,事实也很重要。 但是,事实是好的,只是模型很好,而建立模型是不可靠的职业。 那么多少事实就足够了?

您可以找到序列中的下一个号码吗?
1 2 4 8
如果您需要更多数据来做出决定,这里还有一个数字:
1,2,4,8,16
下一个数字应该是32,对吧? 模式很明确:要查找下一个数字,您需要将前一个数字加倍。 1×2 = 2; 2×2 = 4; 4×2 = 8; 8×2 =16。因此,下一个数字应为16×2 =32。要确认这一点还需要多少事实?
但是,尽管可以合理地假设下一个数字为32,但这并不总是正确的。 考虑以下顺序:我们将计算圆被连接在圆上的点的线所划分的部分的数量。
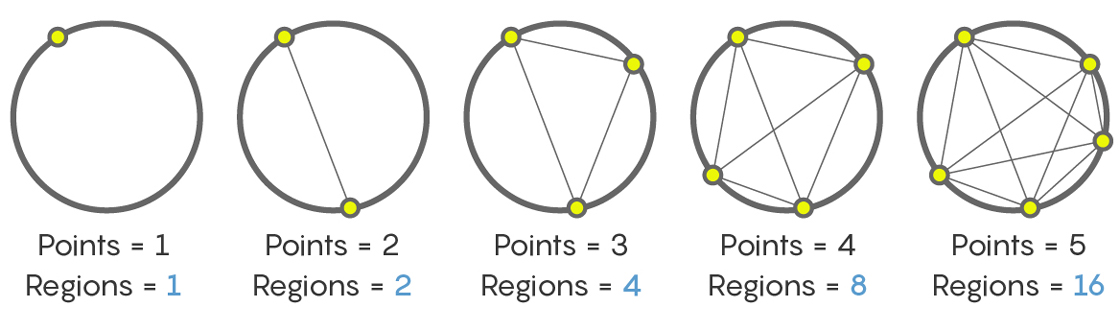
1个点给出一个部分(圆的整个内部)。 两点-两节。 三分-四个部分。 五和六分别是八和十六。 结果是一个序列
1,2,4,8,16
连接圆上六个点的线后会出现多少个部分? 如果您像许多第一次面对这项任务的人一样,没有人会谴责您说32。但是事实并非如此。 实际上,无论多么烦人,答案都是-31! 重新叙述一下自己,然后再次检查。
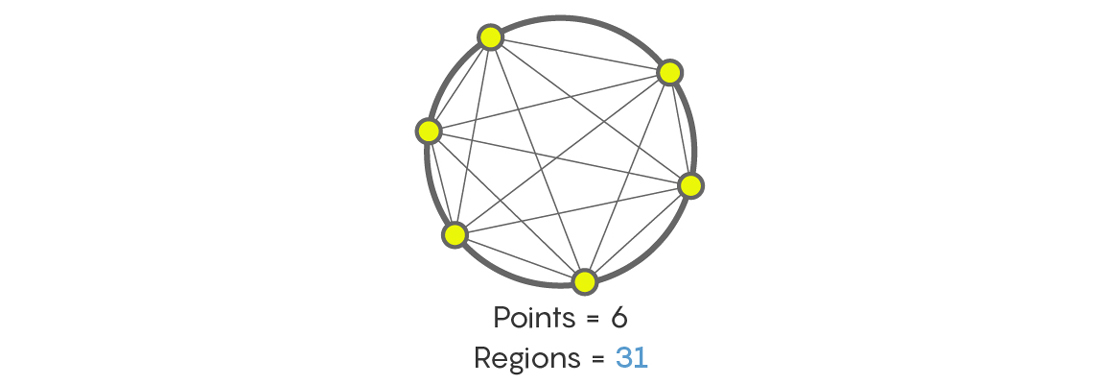
当然,有一些序列,例如1、2、4、8、16、32、64,依此类推,每次的数目加倍。 但是,还有其他序列,例如,用连接圆点上的点的线将圆划分成的最大部分数,这是1、2、4、8、16、31、57、99,依此类推。 满足顺序1、2、4、8、16,我们可能会认为所有事实都是下一个数字将是32,但是可能还有其他情况。
数学具有挑战我们的期望并发挥想象力的悠久传统。 因此,数学家们总是努力获得严格的证明,而不仅仅是事实。 证明建立了数学真理。 所有事实都可能指向32作为我们序列中的下一个数字,但是如果没有严格的证据,我们将无法确定。
但是,对于数学家来说,事实是有用且重要的。 在证明某些东西之前,我们经常玩弄可用的信息,研究问题,考虑示例并收集数据。 我们研究并权衡事实,然后决定下一步要做什么。 这些结果构成了我们的观点,建议证明一些定理而反驳其他定理。
孪生素数假设是一个例子,其中事实以与证明相同的方式控制着我们的数学思维。 孪生素数是相差2的素数对-例如,3和5、11和13、101和103。孪生素数的假设表明,此类孪生素没有最大的一对-也就是说,相似移到无穷大时,对一直在数字线上出现。
孪生素数假设不是一个定理,因为尽管这是数论中最著名的问题之一,但尚无人能证明它。 但是,几乎所有的人都认为它是真的,因为它有很多事实支持。
例如,在寻找素数时,我们不断发现非常大的双素数对。
今天,已知最大
对的每个质数都包含40万个数字。 还证明了与该假设相似的定理。 2013年,
Zhang Ethan证明存在无限数量的素数对,相差不超过7000万,震惊了数学界。 感谢随后的开放式
Polymath项目,我们知道有无数个素数对相差
不超过246 。 我们还没有证明存在无限数量的素数对,它们之间相差2-但2仍然比246更接近于246,而不是246等于无穷大。
由于这些和其他原因,即使没有证实假设,对正义的信仰也没有引起很大争议。 但是,在数学的其他领域中,事实被用来建立见多识广的观点,而事实证明这些观点更具争议性。
在研究椭圆曲线时,粗略地说,其等级表示求解该曲线的复杂程度的数值估计。 多年以来,人们一直认为
椭圆曲线的
等级不受限制 ,也就是说,对曲线的等级值或解的复杂性没有限制。
但是,最近的工作使数学家考虑了有限排名的可能性。 该论文给出的事实表明,可能存在数量有限的,其秩大于21的曲线。
但是,建议谨慎。 数学家收集的事实并非来自椭圆曲线的世界-它们与研究人员用来对曲线建模的矩阵有关。 数学模型在科学中被广泛使用,甚至可以向内转以研究数学本身。 这些功能强大到令人难以置信的工具,可让我们用更容易应对的任务代替难以理解的任务。
但是使用模型是一件棘手的事情。 您永远无法确定模型的行为与我们试图理解的模型非常相似,以便我们可以从模型的行为中得出结论。 同样,我们无法确定在最重要的地方我们的模型是否精确相似。 因此,很难确保我们在模型的基础上收集到的事实确实证明了我们正在研究的现象的真实性质。 让我们基于简单假设的简单模型来研究这些问题。
假设我们要研究以下语句:任意两行是相交或平行的。
交点是指公共点中存在直线,而平行度是指它们沿一个方向但不相交(这一概念可以不同地定义,但为简单起见,我将使用它)。
要研究此问题,请创建一个模型。 每条线由斜线方程表示,您可以从学校课程中记住该方程。 也就是说,我们假设每一行都可以用以下形式的方程式描述
y = mx + b
其中,m是直线的斜率(陡度),b是y轴(垂直轴)的交点。
以这种方式对线进行建模方便于对其进行实验。 该模型允许我们通过选择一对随机数m和b来创建一条随机线。 我们可以选择一对随机线并进行检查-它们是否相交? 他们会走一条路吗? 还有什么事吗
以下是这些实验结果可能看起来如何的一些示例。
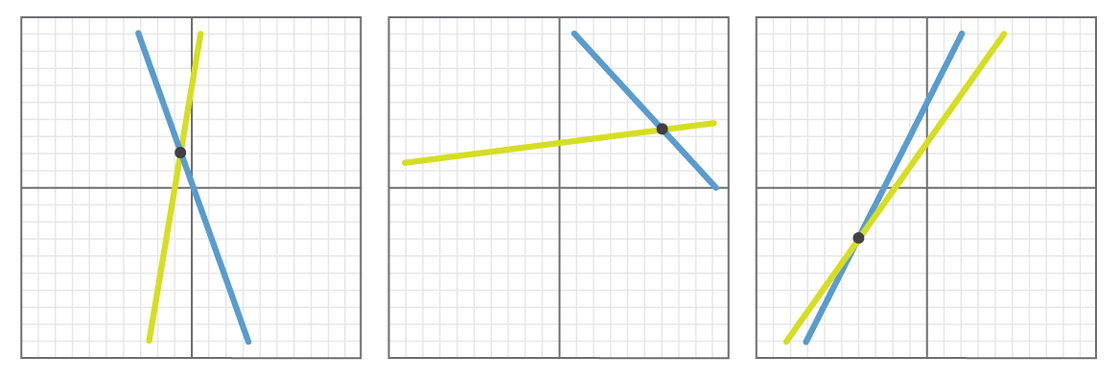
在每个示例中,随机选择的线相交。 如果我们进行此实验一千次-或10,000或一百万次-我们会发现在所有情况下这些线都将相交或平行(并且很可能所有线都将相交,因为两条线不太可能具有相同的斜率,因此选择偶然)。
因此,查看一百万个示例,您可以得出结论,该假设很可能是正确的。 所有事实完全支持任何一对线是平行或相交的说法。
但是,事实和模型一样好,而且建模很危险。 让我们看看在示例中我们为自己带来的危险。
一个问题是某些类型的线会比其他类型的线更常见。 这是显示50条线的图形,其中b = 0且0≤m≤1。
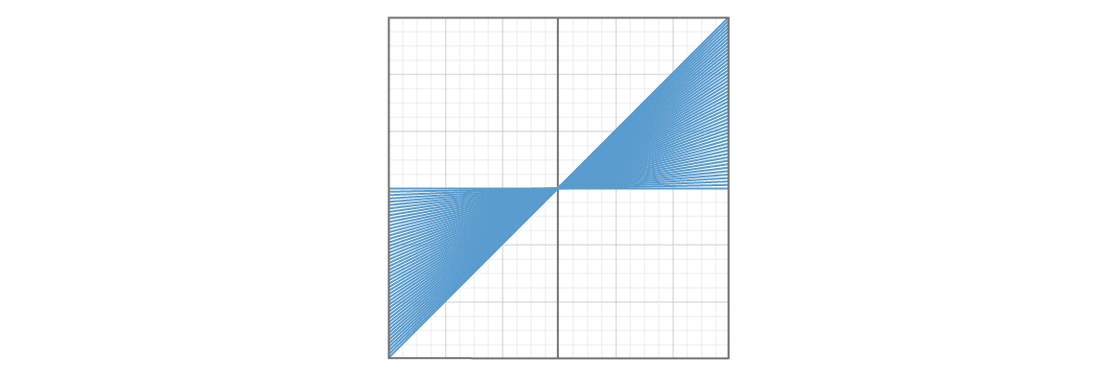
这是显示50条线的图形,其中b = 0和m≥1。

看起来该平面的四分之一被斜率从0到1的直线覆盖,而另一四分之一被斜率大于1的直线覆盖。选择一个大于1的数字似乎比从0到1选择一个数字更有可能。将在飞机的第二部分。 这意味着斜率从0到1的某些线在模型中将很少显示。 而且,如果在飞机的这一部分上发生了一些奇怪的事情,这些直线都是直线,那么我们的模型就不太可能告诉我们这一点。
如果您仔细观察第二张图表,我们将看到另一个问题。 m越大,直线越陡。 最酷的直线是垂直的。 垂直线的斜率是多少? 根据定义,它没有定义:没有这样的数字m可以描述垂直线。 事实证明,我们的模型中没有垂直线,我们无法对其进行实验。 我们尚未开始收集事实,但是仅由于模型构建方案就已经排除了一些特殊情况。
这同样关系到我们模型中最严重的问题。 容易想象三维空间的人们可能会立即注意到我们的假设是错误的。 直线不必相交或平行。 想象一下,在建筑物的不同楼层上有两个朝着不同方向的走廊。 这些是相交的直线-不相交且不平行的直线。
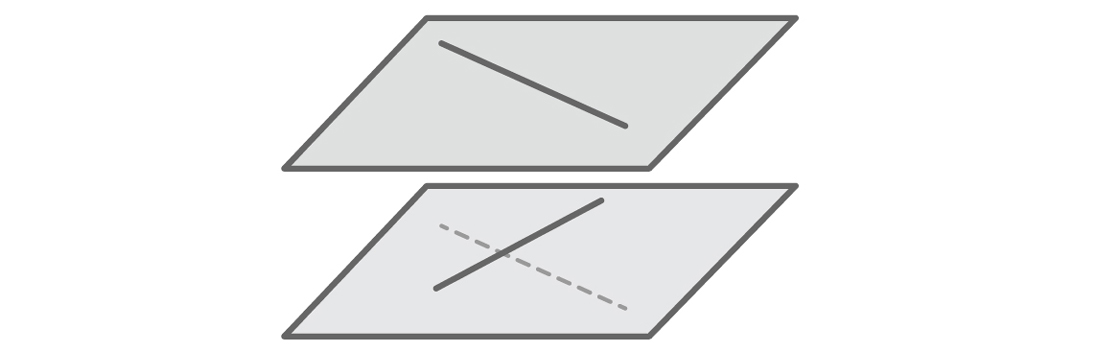
交叉线必须位于不同的平面上。 但是,由于我们的模型通过等式y = mx + b定义了任何线,因此我们自动想象所有线都在同一平面上。 我们的模型只会给出支持我们假设的事实,因为如果两条线位于同一平面上,则它们实际上必须相交或平行。 我们不会看到其他事实:我们的模型中没有相交的线。 与垂直线一样,该模型排除了我们无法想象的情况。
这是一个简单的示例,它使用了一个愚蠢的模型,存在很多问题,其中包括棘手的问题,例如从无限集中选择随机数的过程。 研究椭圆曲线等级的专业数学家永远不会犯过如此简单而明显的错误。
这些数学家知道使用模型时应采取的预防措施。 他们知道,不管模型将多么有用和有趣,或者说服所收集的事实有多令人信服,椭圆曲线都可能显示出他们无法想象的特性。 而且如果无法想象,您的模型将不会考虑到这一点,因此事实将不会得到反映。
但是,无论新模型是否正确,它都迫使数学家对椭圆曲线进行富有成效的思考。 如果它真实地反映了事实,那么矩阵世界的想法就可以解释曲线的行为。 如果不是这样,那么了解为什么不能以这种方式建模椭圆曲线可以更好地理解问题。 我们收集的事实可以使我们以一种或另一种方式更接近证明。