🤦 ⛄️ 🥥 卷积层：矩阵乘法优化技术 ♏️ 🔢 🚣🏾

引言

本文是描述基础算法的一系列文章的续篇。
Synet是用于在CPU上启动预训练的神经网络的框架。

如果看一下在神经网络中直接信号传播所花费的处理器时间的分布，事实证明，通常有90％以上的时间都用在卷积层上。因此，如果要获得用于神经网络的快速算法，首先需要针对卷积层的快速算法。在本文中，我想描述优化卷积层中直接信号传播的方法。我想从基于矩阵乘法的最广泛使用的方法开始。我将尝试使演示文稿保持最易于访问的形式，以便使这篇文章不仅对专家（他们已经知道有关它的一切）都很有趣，而且也使更广泛的读者感兴趣。我不假装是一个完整的评论，因此仅欢迎任何评论和补充。

卷积层选项

我想从对卷积层中参数的描述开始描述。专家可以放心地跳过此部分。

输入和输出图像大小

首先，卷积层的特征在于输入和输出图像，其特征在于以下参数：

srcC / dstC-输入和输出图像中的通道数。替代符号： C / D。
srcH / dstH-输入和输出图像的高度。替代名称： H。
srcW / dstW-输入和输出图像的宽度。替代名称： W.
批 -输入（输出）图像的数量-该层一次可以处理整批图像。替代名称： N。

卷积核大小

卷积运算本质上是图像中给定点的某个邻域的加权和。卷积核的大小-表征此邻域的大小，并由两个参数描述：

kernelY是卷积核的高度。替代名称： Y。
kernelX是卷积内核的宽度。替代名称： X。

最常见的卷积，内核大小为1x1和3x3 。尺寸5x5和7x7不太常见。有时还会发现较大的卷积大小，以及与除正方形以外的其他内核的卷积，但这更加奇特。

卷积步骤

另一个重要参数是卷积步骤：

strideY是垂直卷积步骤。
strideX-水平卷积步骤。

如果步长不同于1x1 ，例如-2x2 ，则输出图像将是原来的一半（仅在偶数点附近计算卷积）。

拉伸卷积

使用以下参数可以扩展卷积内核（在保持操作数的同时增加有效窗口大小）：

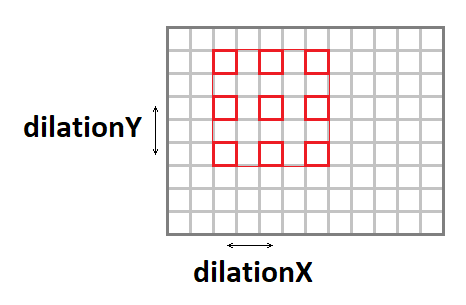
扩张 -卷积的垂直拉伸。
dilationX-卷积的水平拉伸。

值得注意的是，除1x1以外的其他情况很少见（我在职业生涯中从未遇到过这种情况）。

填充输入图像

如果对图像应用与单个窗口不同的卷积，则输出图像将减少内核-1的量。束原样“吞噬”了边缘。为了保持图像的大小，通常在输入图像的边缘周围用零填充。另有四个参数对此负责：

padY / padX-正面垂直和水平填充。
padH / padW-后垂直和水平填充。

频道组

通常，每个输出通道是所有输入通道上的卷积之和。但是，并非总是如此。可以将输入和输出通道划分为组，求和仅在组内进行：

组 - 组数。

实际上，最经常遇到的情况是group = 1且group = srcC = dstC ，即所谓的深度卷积 。

位移和启动功能

尽管从形式上说，位移和激活函数不包括在卷积中，但是这两个操作经常遵循卷积层，因此为什么它们通常也包含在卷积层中。考虑到各种可能的激活函数及其参数，在此不再赘述。

算法的基本实现

首先，我想给出该算法的基本实现：

float relu(float value) { return value > 0 ? return value : 0; } void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; for (int b = 0; b < batch; ++b) { for (int g = 0; g < group; ++g) { for (int dc = 0; dc < dstC / group; ++dc) { for (int dy = 0; dy < dstH; ++dy) { for (int dx = 0; dx < dstW; ++dx) { float sum = 0; for (int sc = 0; sc < srcC / group; ++sc) { for (int ky = 0; ky < kernelY; ky++) { for (int kx = 0; kx < kernelX; kx++) { int sy = dy * strideY + ky * dilationY - padY; int sx = dx * strideX + kx * dilationX - padX; if (sy >= 0 && sy < srcH && sx >= 0 && sx < srcW) sum += src[((b * srcC + sc)*srcH + sy)*srcW + sx] * weight[((dc * srcC / group + sc)*kernelY + ky)*kernelX + kx]; } } } dst[((b * dstC + dc)*dstH + dy)*dstW + dx] = relu(sum + bias[dc]); } } } } } }

在此实现中，我假设输入和输出图像为NCHW格式：

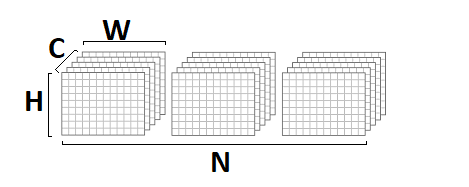
卷积权重以DCYX格式存储，我们的激活函数是ReLU 。在一般情况下，情况并非如此，但是对于基本实现而言，这样的假设是非常合适的-您必须从某些方面入手。

我们有8个嵌套循环和操作总数：

 batch * kernelY * kernelX * srcC * dstH * dstW * dstC / group * 2,

而输入的数据量：

 batch * srcC * srcH * srcW,

并输出图像：

 batch * dstC * dstH * dstW,

和重量数：

 kernelY * kernelX * srcC * dstC / group.

如果组<< srcC （组的数量远小于通道的数量），并且具有足够大的参数srcC ， srcH ， srcW和dstC ，则当计算数量大大超过输入和输出数据量时，我们将遇到经典的计算问题。即具有正确实现方式的卷积运算应取决于处理器的计算资源，而不取决于存储器带宽。仍然只有找到此实现。

将问题简化为矩阵乘法

卷积的主要操作是获得加权和，并且输出图像的所有点的权重均相同。如果按以下方式重新排列输入图像：

 void im2col(const float * src, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; for (int sc = 0; sc < srcC; ++sc) { for (int ky = 0; ky < kernelY; ky++) { for (int kx = 0; kx < kernelX; kx++) { for (int dy = 0; dy < dstH; ++dy) { for (int dx = 0; dx < dstW; ++dx) { int sy = dy * strideY + ky * dilationY - padY; int sx = dx * strideX + kx * dilationX - padX; if (sy >= 0 && sy < srcH && sx >= 0 && sx < srcW) *buf++ = src[((b * srcC + sc)*srcH + sy)*srcW + sx]; else *buf++ = 0; } } } } } }

然后，我们将从srcC-srcH-srcW格式切换到srcC-kernelY-kernelX-dstH-dstW格式 。下图显示了如何使用填充1和3x3核心转换图像：

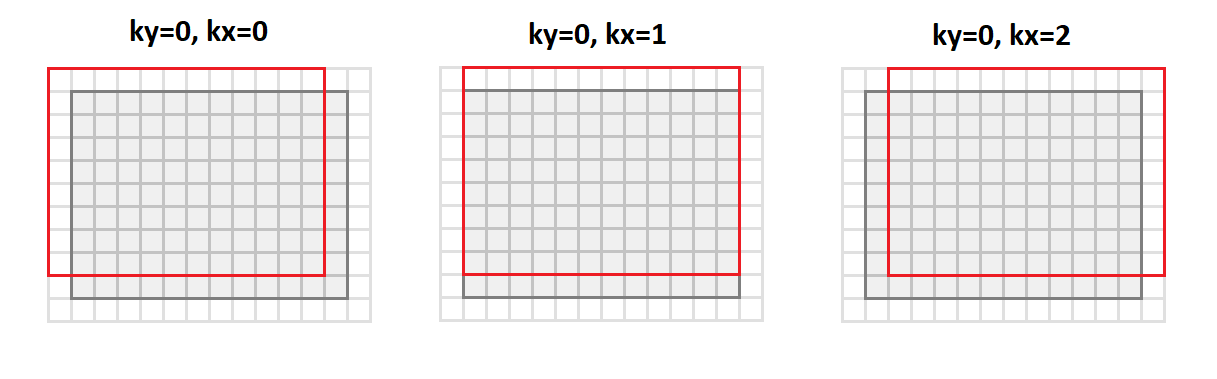
在这种情况下，卷积运算所需的图像邻域的所有点均沿结果矩阵的列对齐（因此，其名称为-图像的列数）。

输入图像的新表示形式很有趣，因为现在我们中的卷积运算被简化为矩阵乘法：

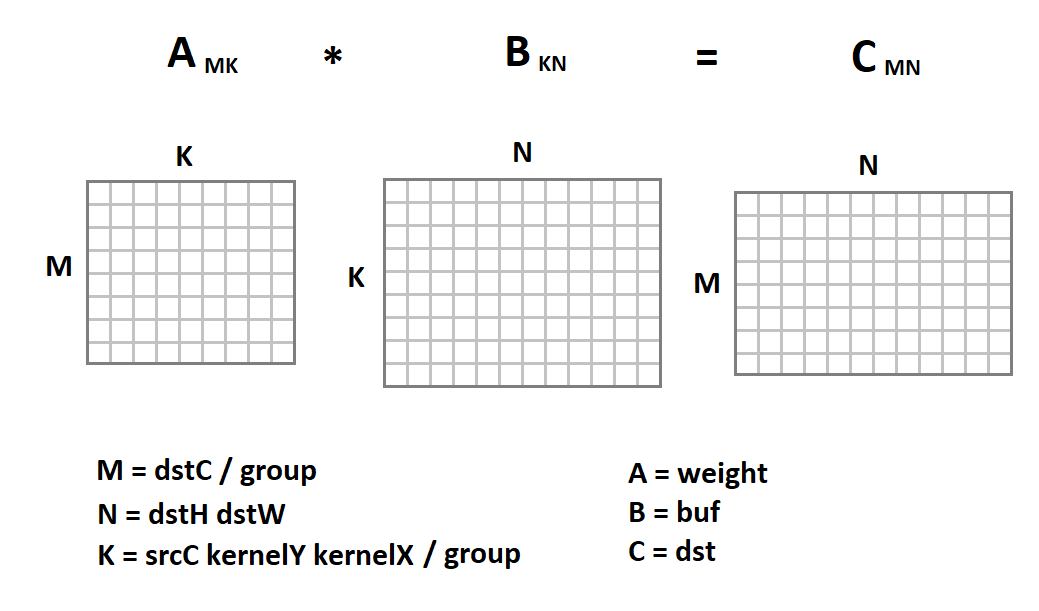
现在，卷积代码将如下所示：

 void gemm_nn(int M, int N, int K, float alpha, const float * A, int lda, float beta, const float * B, int ldb, float * C, int ldc) { for (int i = 0; i < M; ++i) { for (int j = 0; j < N; ++j) { C[i*ldc + j] = beta; for (int k = 0; k < K; ++k) C[i*ldc + j] += alpha * A[i*lda + k] * B[k*ldb + j]; } } } void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; int M = dstC / group; int N = dstH * dstW; int K = srcC * kernelY * kernelX / group; for (int b = 0; b < batch; ++b) { im2col(src, srcC, srcH, srcW, kernelY, kernelX, dilationY, dilationY, strideY, strideX, padY, padX, padH, padW, buf); for (int g = 0; g < group; ++g) gemm_nn(M, N, K, 1, weight + M * K * g, K, 0, buf + N * K * g, N, dst + M * N * g, N)); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } }

这里，矩阵乘法的简单实现仅作为示例给出。我们可以将其替换为任何其他实现。幸运的是，矩阵乘法是一项历史悠久的操作，已经在许多库中以非常高的效率实现（高达理论上可能的CPU性能的90％）。关于如何实现这种效率的主题，我什至有另一篇文章。

对NHWC格式使用矩阵乘法

与NCHW格式一起， NHWC通常用于机器学习中：

例如，请注意NHWC是本机Tensorflow格式。

值得注意的是，对于这种格式，卷积运算也可以导致矩阵乘法。为此，使用im2row函数，将格式为srcH-srcW-srcC转换为dstH-dstW-kernelY-kernelX-srcC 格式：

 void im2row(const float * src, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; for (int g = 0; g < group; ++g) { for (int dy = 0; dy < dstH; ++dy) { for (int dx = 0; dx < dstW; ++dx) { for (int ky = 0; ky < kernelY; ky++) { for (int kx = 0; kx < kernelX; kx++) { int sy = dy * strideY + ky * dilationY - padY; int sx = dx * strideX + kx * dilationX - padX; for (int sc = 0; sc < srcC; ++sc) { if (sy >= 0 && sy < srcH && sx >= 0 && sx < srcW) *buf++ = src[(sy * srcW + sx)*srcC + sc]; else *buf++ = 0; } } } } } src += srcC / group; } }

而且，卷积运算所需的图像邻域的所有点都沿着所得矩阵的行对齐（因此，其名称为-图像到行 s）。我们还应该将卷积音阶的存储格式从DCYX格式更改为YXCD格式。现在我们可以应用矩阵乘法：

与NCHW格式不同，我们将图像矩阵乘以权重矩阵，反之亦然。以下是卷积函数代码：

 void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; int M = dstH * dstW; int N = dstC / group; int K = srcC * kernelY * kernelX / group; for (int b = 0; b < batch; ++b) { im2row(src, srcC, srcH, srcW, kernelY, kernelX, dilationY, dilationY, strideY, strideX, padY, padX, padH, padW, group, buf); for (int g = 0; g < group; ++g) gemm_nn(M, N, K, 1, buf + M * K * g, K * group, 0, weight + N * g, dstC, dst + N * g, dstC)); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } }

该方法的优缺点

从一开始，我想列出这种方法的优点：

此方法的实现非常简单。我知道几乎所有库都使用了它。
该方法在许多情况下的有效性非常高：从基本版本中的百分比单位，我们可以达到理论最大值的80％以上。
该方法是通用的-对于卷积层的所有可能参数，我们只有一个代码（而且有很多！）。因此，这种方法通常在更有效（因此更专业）的方法存在局限性的情况下起作用。
该方法适用于图像张量的主要格式-NCHW和NHWC 。

现在来谈谈缺点：

不幸的是，只要参数M，N，K的值足够大，而且它们的大小近似相同，则标准矩阵乘法是有效的（效率基于以下事实：所需的计算数量为〜O（N ^ 3）和所需的吞吐量记忆能力〜O（N ^ 2） ）。因此，如果参数M，N，K中的任何一个较小，则该方法的效率将急剧下降。
该方法需要输入数据的转换。这远非自由操作。仅当K足够大时，她才能被忽略。而且如果我们考虑到在标准矩阵乘法内部仍然存在输入数据的内部转换，那么情况将变得更加糟糕。
基于K = srcC * kernelY * kernelX / group的事实，该方法对于输入卷积层的效率特别低。对于深度卷积，矩阵方法通常会失败于简单的实现。
该方法需要对输出数据进行附加处理，以进行换档操作和激活函数的计算。
有更有效的数学方法来计算卷积，需要较少的运算。

结论

基于矩阵乘法的卷积计算方法实现简单，效率高。不幸的是，它不是通用的。对于许多特殊情况，有更快的方法，我想将其描述推迟到本系列的下一篇文章中。等待读者的反馈和意见。希望你有兴趣！

PS这种方法和其他方法是由我在卷积框架中作为Simd库的一部分实现的。
该框架是Synet的基础， Synet是用于在CPU上运行预训练的神经网络的框架。

卷积层：矩阵乘法优化技术

引言