前言
不久之前,我不得不简化多边形链(该
过程可以减少折线点的数量 )。 通常,在处理矢量图形和构建地图时,此类任务非常常见。 例如,我们可以采用一条链,该链的几个点落在同一像素中-显然所有这些点都可以简化为一个。 不久前,我几乎从“完全”一词一无所知,因此,我不得不快速填写有关该主题的必要知识。 但是,当我在Internet上找不到足够完整的手册时,我感到很惊讶……我不得不从完全不同的来源中搜索摘录中的信息,然后经过分析,将所有内容都整理成了一张大图。 老实说,职业不是最愉快的事情之一。 因此,我想写一系列有关多边形链简化算法的文章。 我刚决定从最受欢迎的Douglas-Pecker算法开始。
内容描述
该算法设置初始折线和最大距离(ε),该距离可以在原始折线和简化折线之间(即,从原始点到生成折线的最近部分的最大距离)。 该算法以递归方式划分折线。 该算法的输入是第一个点与最后一个点之间的所有点的坐标(包括它们)以及ε的值。 第一点和最后一点保持不变。 之后,该算法找到距离由第一个和最后一个组成的分段最远的点(
搜索算法是从该点到分段的距离 )。 如果该点的距离小于ε,则可以从集合中弹出所有尚未标记为要存储的点,并且所得直线以至少ε的精度平滑曲线。 如果此距离大于ε,则算法会从起点到给定点以及从给定点到终点递归调用集合。
值得注意的是,道格拉斯-佩克算法在其工作过程中并未保留拓扑。 这意味着结果是,我们可以获得带有自相交的线。 作为说明性示例,采用具有以下点集的折线:[{1; 5},{2; 3},{5; 1},{6; 4},{9; 6},{11; 4},{13; 3},{14; 2},{18; 5}],然后查看不同ε值的简化过程:
提出的一组点中的原始折线:

折线ε等于0.5:
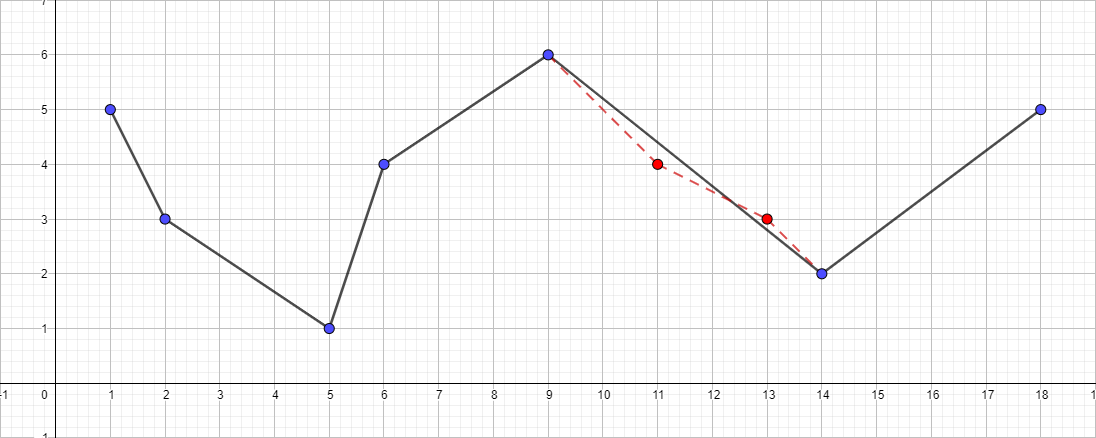
ε等于1的折线:

折线ε等于1.5:
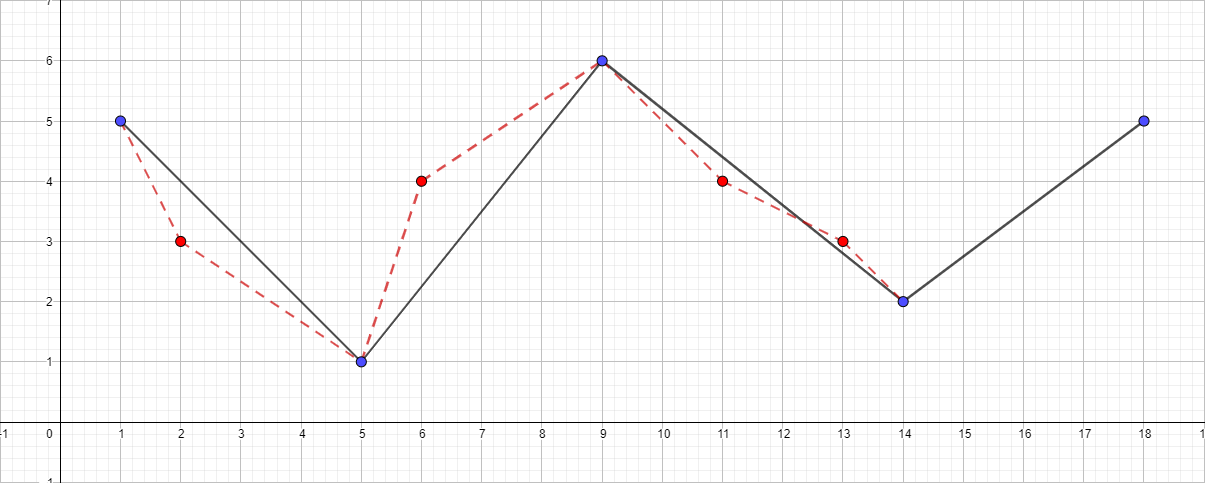
您可以继续增加最大距离并可视化该算法,但是,我认为,这些示例之后的要点已经很清楚了。
实作
选择C ++作为实现该算法的编程语言,您可以
在此处查看该算法的完整源代码。 现在直接转到实现本身:
#define X_COORDINATE 0 #define Y_COORDINATE 1 template<typename T> using point_t = std::pair<T, T>; template<typename T> using line_segment_t = std::pair<point_t<T>, point_t<T>>; template<typename T> using points_t = std::vector<point_t<T>>; template<typename CoordinateType> double get_distance_between_point_and_line_segment(const line_segment_t<CoordinateType>& line_segment, const point_t<CoordinateType>& point) noexcept { const CoordinateType x = std::get<X_COORDINATE>(point); const CoordinateType y = std::get<Y_COORDINATE>(point); const CoordinateType x1 = std::get<X_COORDINATE>(line_segment.first); const CoordinateType y1 = std::get<Y_COORDINATE>(line_segment.first); const CoordinateType x2 = std::get<X_COORDINATE>(line_segment.second); const CoordinateType y2 = std::get<Y_COORDINATE>(line_segment.second); const double double_area = abs((y2-y1)*x - (x2-x1)*y + x2*y1 - y2*x1); const double line_segment_length = sqrt(pow((x2-x1), 2) + pow((y2-y1), 2)); if (line_segment_length != 0.0) return double_area / line_segment_length; else return 0.0; } template<typename CoordinateType> void simplify_points(const points_t<CoordinateType>& src_points, points_t<CoordinateType>& dest_points, double tolerance, std::size_t begin, std::size_t end) { if (begin + 1 == end) return; double max_distance = -1.0; std::size_t max_index = 0; for (std::size_t i = begin + 1; i < end; i++) { const point_t<CoordinateType>& cur_point = src_points.at(i); const point_t<CoordinateType>& start_point = src_points.at(begin); const point_t<CoordinateType>& end_point = src_points.at(end); const double distance = get_distance_between_point_and_line_segment({ start_point, end_point }, cur_point); if (distance > max_distance) { max_distance = distance; max_index = i; } } if (max_distance > tolerance) { simplify_points(src_points, dest_points, tolerance, begin, max_index); dest_points.push_back(src_points.at(max_index)); simplify_points(src_points, dest_points, tolerance, max_index, end); } } template< typename CoordinateType, typename = std::enable_if<std::is_integral<CoordinateType>::value || std::is_floating_point<CoordinateType>::value>::type> points_t<CoordinateType> duglas_peucker(const points_t<CoordinateType>& src_points, double tolerance) noexcept { if (tolerance <= 0) return src_points; points_t<CoordinateType> dest_points{}; dest_points.push_back(src_points.front()); simplify_points(src_points, dest_points, tolerance, 0, src_points.size() - 1); dest_points.push_back(src_points.back()); return dest_points; }
好吧,实际上是算法本身的使用:
int main() { points_t<int> source_points{ { 1, 5 }, { 2, 3 }, { 5, 1 }, { 6, 4 }, { 9, 6 }, { 11, 4 }, { 13, 3 }, { 14, 2 }, { 18, 5 } }; points_t<int> simplify_points = duglas_peucker(source_points, 1); return EXIT_SUCCESS; }
算法执行示例
作为输入,我们采用一组较早的已知点[{1; 5},{2; 3},{5; 1},{6; 4},{9; 6},{11; 4},{13; 3},{14; 2},{18; 5}]和ε等于1:
- 找到距段{1; 5}-{18; 5},该点将是点{5; 1}。
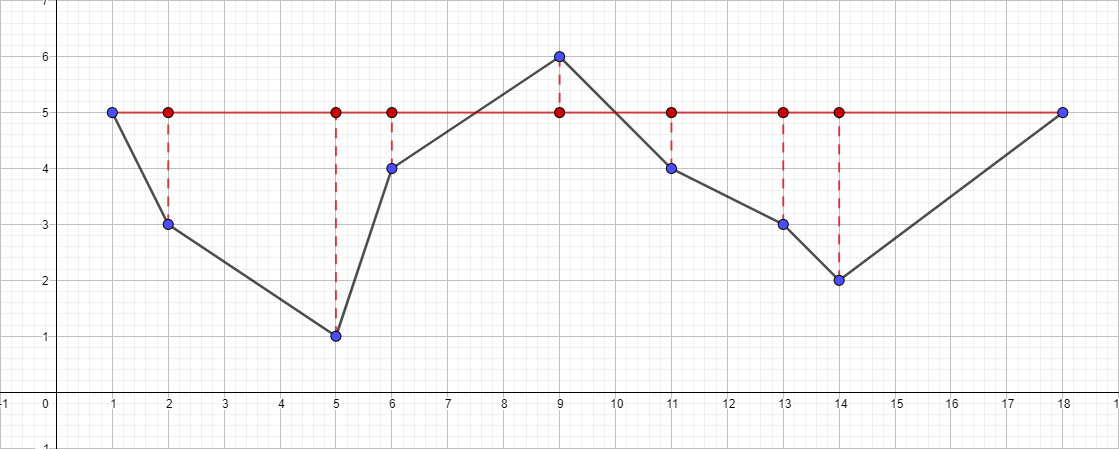
- 检查其与段{1;的距离。 5}-{18; 5}。 结果是大于1,这意味着我们将其添加到生成的折线中。
- 递归地运行段{1; 5}-{5; 1},然后找到此线段的最远点。 这是{2; 3}。
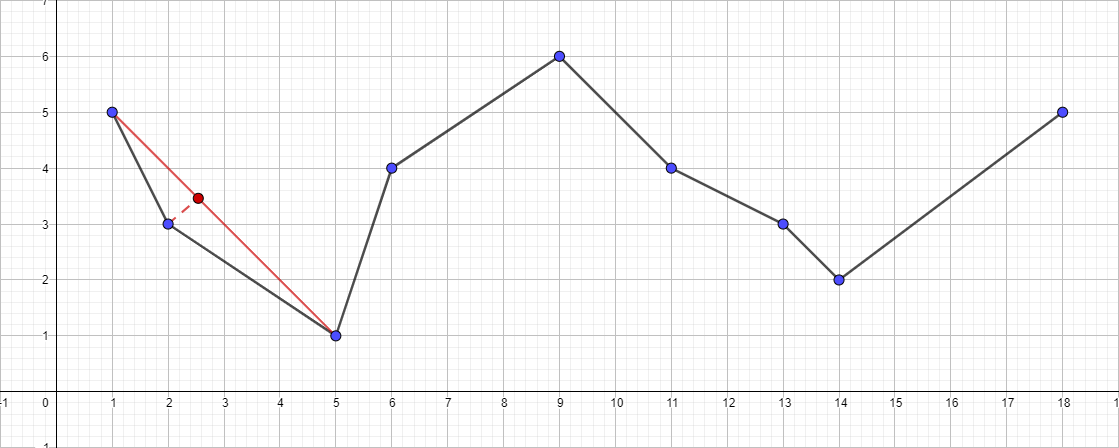
- 检查其与段{1;的距离。 5}-{5; 1}。 在这种情况下,它小于1,这意味着我们可以安全地丢弃此点。
- 递归地运行段{5; 1}-{18; 5}并找到该线段的最远点...
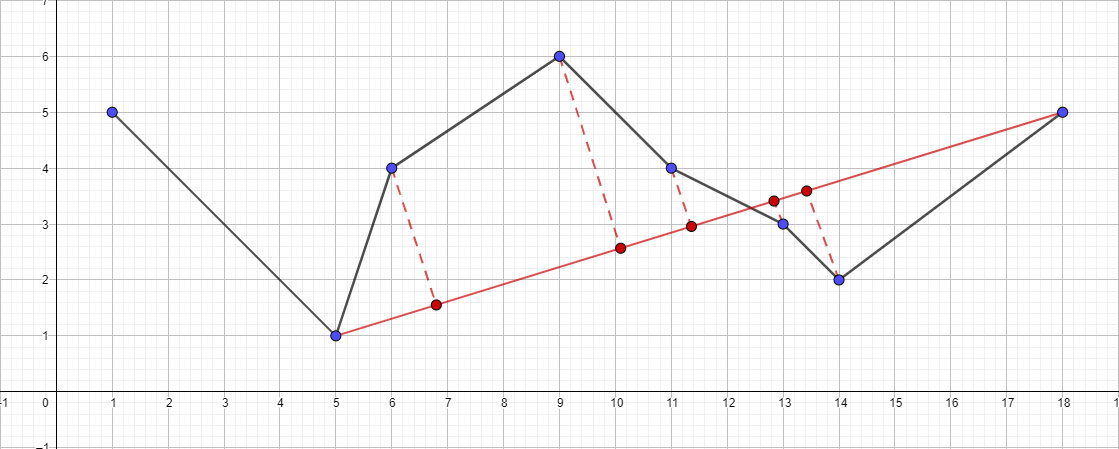
- 依此类推,依此类推...
结果,此测试数据的递归调用树将如下所示:
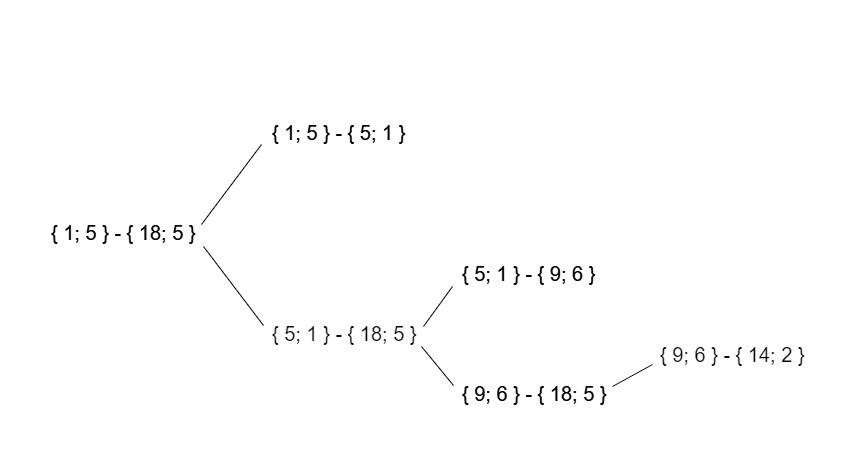
工作时间
该算法的预期复杂度充其量为O(nlogn),这是最远点的数量始终按字典顺序为中心的情况。 但是,在最坏的情况下,算法的复杂度为O(n ^ 2)。 例如,如果最远点的数量始终与边界点的数量相邻,则可以实现此目的。
我希望我的文章对某人有用,我也想提请注意一个事实,如果该文章在读者中引起了足够的兴趣,我将很快准备考虑简化Reumman-Witkam,Opheim和Lang的多边形链的算法。 感谢您的关注!