通常，在分析通过实验获得的平稳时间序列时，在数据的初步准备（预处理）期间，必须抑制其中存在的趋势。
这里将提出一种“新的”趋势突出显示方法-简单，明显且适用于非常复杂的趋势类型。
通常将趋势理解为一种超低频非谐波分量，它严重违反了过程的平稳性。 实验获得的数据趋势的最常见原因是记录设备的“零漂移”。 数据集成和某些其他类型的处理也会引起趋势。 趋势的存在极大地扭曲了后续数据处理（频谱估计等）的结果，因此，有必要消除趋势。 在某些情况下，趋势本身是有价值的信息来源（例如，在分析经济或气象过程的长期趋势时）。
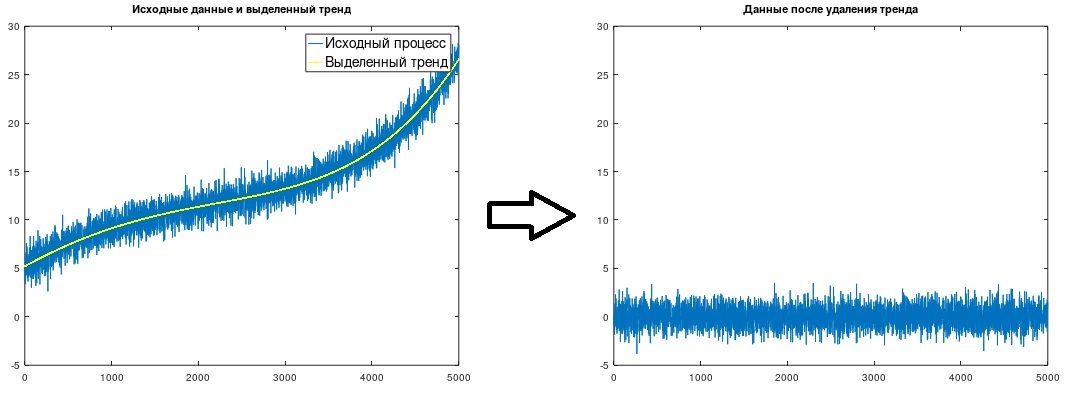图 1.隔离和消除趋势通常，趋势是使用线性或幂（二阶或三阶）函数建模的，其系数是通过将过程乘以某些序列，然后应用使用最小二乘法得出的相当复杂的公式来计算的。 （例如，参见J. Bendat，A. Pirsol，“随机数据的应用分析”，M.，Mir，1989年。）以下是略微修改的方法，同样基于最小二乘法，该方法非常易于理解和学习，并且不需要引用目录或独立的复杂符号计算来获得必要的依赖关系，同时允许您使用任何类型的函数对趋势进行建模。 这种修改过的方法是如此简单和明显（一旦掌握后，便可以从内存中编写脚本），以至于它可能是不止一次地被不同的研究人员“发明”的，但是我在任何来源中都没有发现任何东西。
为了突出趋势，使用构成趋势u
j [i]的少量k函数对由N + 1个样本组成的初始过程x [i]进行近似处理：
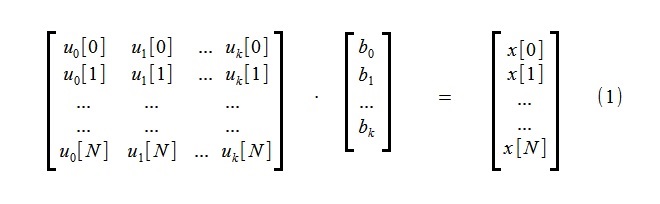
（通常，将幂函数选择为函数u
j [i]，
但对于这种方法，它绝对是无原则的）
线性代数方程组（1）包含k个未知的b
j和N + 1个方程。
采取的符号：
写得更紧凑
最小二乘法在搜索超定系统的近似解中的应用以矩阵形式编写如下：
在编写脚本时：自然地，不需要存储整个大矩阵U，可以逐步“累积”矩阵U
T U和向量U
T x的元素。
k个方程式和k个未知数的系统（4）通过明显的方法求解-好吧，例如，我们这样写：
之后，使用找到的b
j ，我们可以将趋势θ[i]构造为
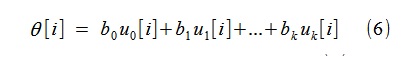
例如，模拟了表格的随机过程x [i]
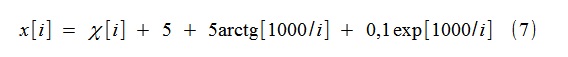
其中χ[i]-具有单个色散的高斯白噪声。 趋势是通过类型（2）（更确切地说是（8））的函数建模的，直到并包括4阶（k = 4）。
当使用幂律函数进行趋势建模时，应注意的是，由于这些函数的线性独立性，矩阵U
T U（4）在理论上始终是可逆的，但是，在k的高阶（或N的很长的实现，这不太关键）时，其某些元素可能非常绝对有价值。 在高k的情况下，在计算困难的情况下，建议使用降低系数，例如，例如（8）：
（Δt= 1），这是在所考虑的示例中完成的。 得到图1所示的趋势。
突出显示趋势之后，自然应该从源数据中减去该趋势。
备注。 通常，权威人士不建议使用k = 2（平方抛物线）以上的趋势模型。 这是否是由于难以
通过传统方法确定“振幅”系数b
j所致，还是由于上述机器变量阶数的用尽，还是该过程的信息成分对趋势的错误分配所致。 在给定的示例中，突出显示了四阶趋势，好像它似乎是合理的（尽管与三阶趋势没有太大区别）。 对于特别困难的情况，消息来源建议使用其他方法-低通滤波（此处不考虑）。
突出显示趋势，如上所示，该过程并不那么复杂，它使您可以选择和分析“慢”趋势，或者更经常地，它有助于获得高质量的数据-适合进一步分析的集中平稳的随机过程。