
引言
本文介绍了在“绝对汇率”项目框架下进行的实验结果。 通过单击链接可以查看实验协议。
“ 绝对汇率 ”项目从事成对汇率的分析,对绝对汇率的分配及其分析。 在该项目的框架内,获得了一种从对汇率转换为绝对汇率的方法。 为此,定义了绝对货币ABS。 所有可用货币均以ABS表示。
在“ 从货币对到绝对汇率 ”一文中对该技术进行了详细说明。
迄今为止,关于绝对汇率方法的应用已经发表了几篇文章。 我带了最后两个。
文章“ 通过绝对汇率的相关性研究世界货币的连通性 ”描述了绝对汇率技术的一种应用。 给出了一种计算不同货币之间关系的正式方法。
文章“ 应用于外汇市场的Markowitz投资组合方法 ”描述了用于优化外汇投资组合的以前无法使用的技术。
下面描述从对(相对)汇率到绝对汇率的转换方法。 给出了转换的数值参数及其计算方法。
在源文件中,每天自动加载每日汇率,并从中计算出绝对汇率。
转换矩阵于2017年获得。 通过使恢复的对汇率与绝对汇率之间的偏差误差最小,以实际汇率计算。 从那时起,就没有对现代数据进行错误分析。
下述意外的验证结果导致了一种获取转换矩阵的新技术的发展。 此外,在处理导入的报价时检测到错误。
理论基础
要获得绝对汇率,您必须进行以下转换。 首先,配对课程是对数。 接下来,我们将它们乘以逆变换矩阵。 最后,我们使用指数从对数刻度返回。
为了进一步过渡到配对课程,必须记录绝对课程。 然后乘以直接变换矩阵。 我们得出与使用指数之前相同的结论。
在“ 从货币对到单个货币的绝对汇率 ”一文中更详细地描述了该技术(与本文的介绍相比,只有2018年的这篇文章给出了转换矩阵的换位表示)。
直接矩阵很容易确定。 其中的行对应于货币,列对应于货币对。 矩阵非常稀疏,由零,一和负一一组成。
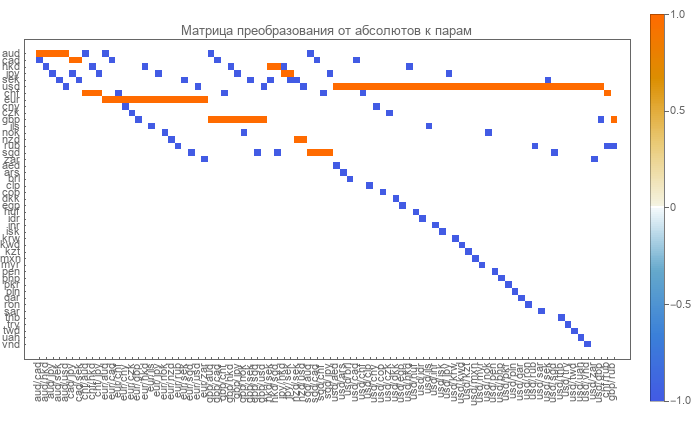
零表示没有这样的货币对和货币。 单位对应于该对分子中的货币。 减一表示货币对中的分母。
没有定义从成对到绝对速率的逆变换矩阵。 必须进行计算。 最明显的方法是使对恢复中的错误最小化。 2017年如何计算此矩阵。 我们给出该矩阵的图形表示。
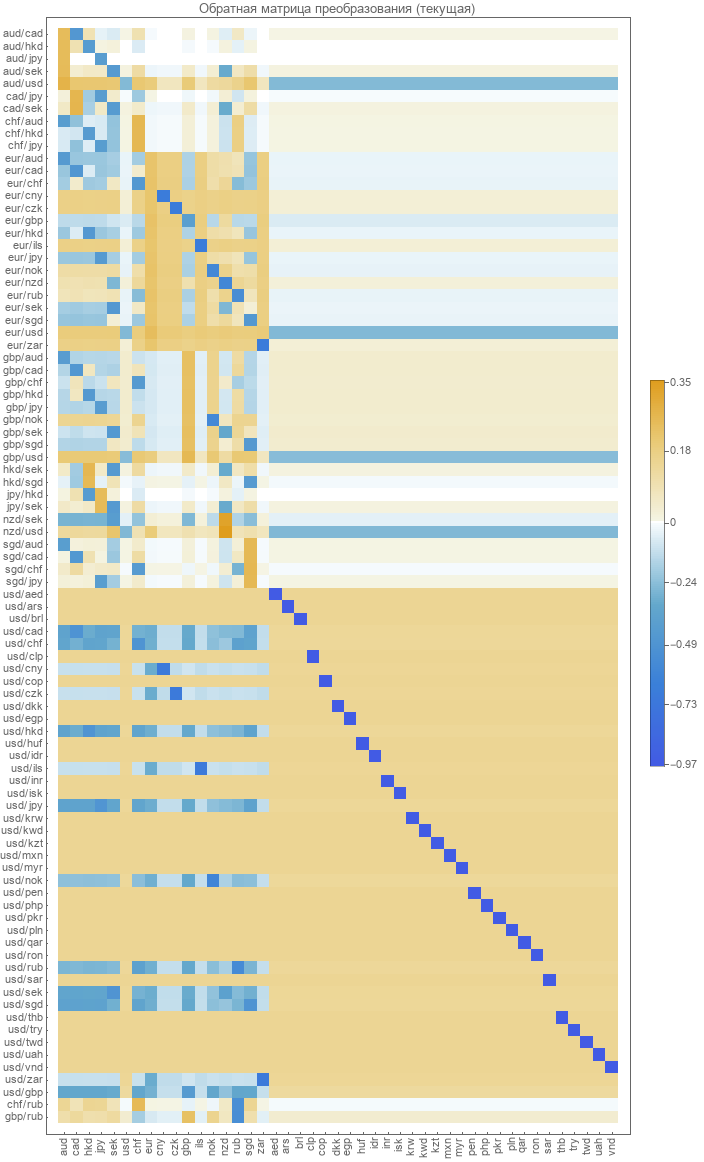
检查现有模型的准确性
对于当前矩阵,获得了绝对汇率和恢复的汇率。 原始配对和恢复配对的课程之间存在明显差异。

接下来,进行所有对的恢复误差的计算。
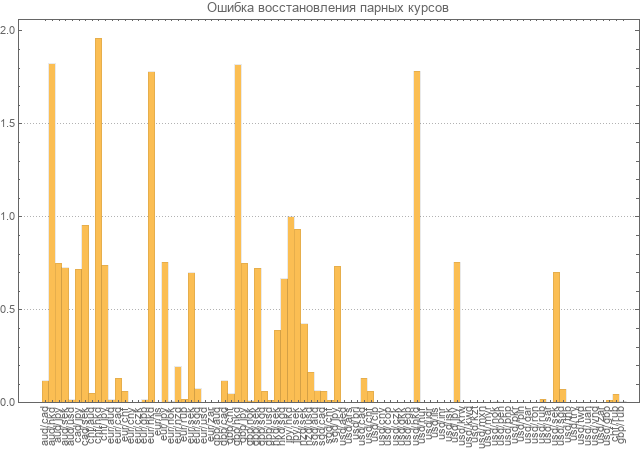
该误差被认为是取模的相对偏差的平均值。 从图中可以看出,许多对的误差几乎是值本身的两倍。
当然,这种误差水平不能使模型被认为是一致的,需要重新计算。
一条线的伪逆矩阵
我们将尝试的第一件事是简单地为直接变换矩阵计算逆矩阵。 由于矩阵是非正方形的,因此我们将不得不使用伪逆变换 。 结果如下。
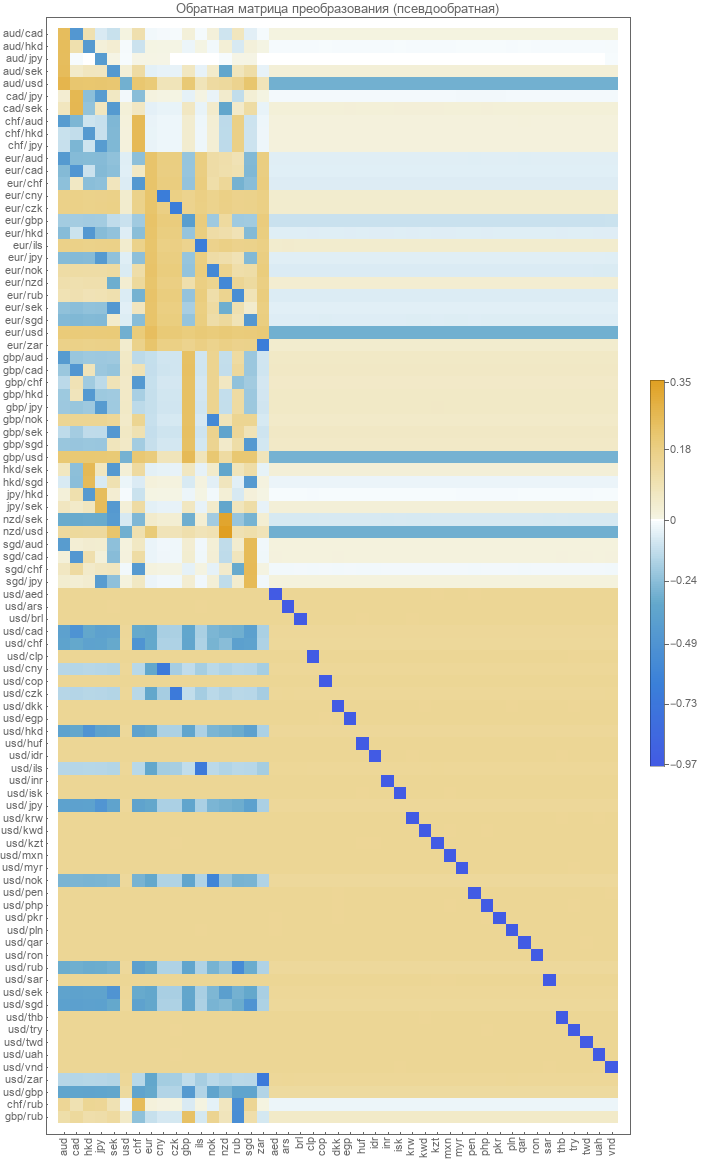
这与我们之前使用实数对汇率进行优化的方法非常相似。
我们计算绝对课程。 然后从绝对配对课程中恢复。 错误图表如下。

与上面的评估一样,误差也很大。 这个模型也不能适合我们。
通过线性独立分量计算逆矩阵
如果我们详细分析直接转换矩阵,我们会发现它具有简并形式 ( 矩阵的等级小于货币行数)。 换句话说,在直接矩阵中有线性相关的行。 因此,我们无法获得可接受的逆矩阵。
为了摆脱这种情况,提出了以下解决方案。 在从绝对路线到成对的过渡中,必须首先切换到线性独立的组件。 然后,继续前进。 从绝对路线到分量路线以及从分量路线到成对路线的过渡矩阵将不会退化,并且可以获得逆矩阵。
为了搜索线性独立的分量,有必要将成对路线的单位矩阵附加到直接变换矩阵上。 因此,我们获得了从绝对路线到成对的过渡的两个矩阵,以及从成对到成对的过渡的附加矩阵。

现在,我们将对该组合矩阵上部的阶梯形式进行标准转换(实际上, Wolfram Mathematica数学软件包的标准工具进一步导致了对角线形式 )。 结果,可以获得下面的变换矩阵。

现在,在此矩阵的列中,我们具有线性独立的组件。 此外,我们可以从绝对路线(矩阵的上部)和配对路线(组合的转换矩阵的下部)两者切换到它们。
我们将这些转换矩阵选为线性独立的分量。 这是绝对课程组成部分的过渡矩阵。
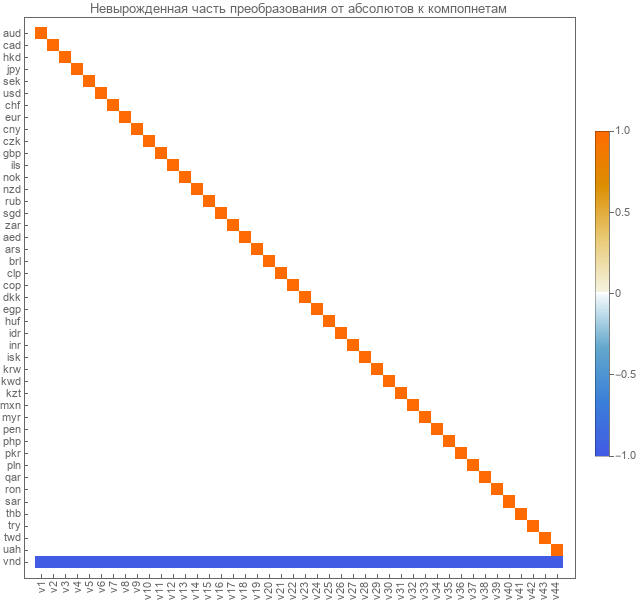
这是从结对路线到线性独立分量的转换矩阵。

从绝对值到分量的转换通过上面计算的矩阵发生。 从分量到绝对值的逆变换是通过逆矩阵完成的。 由于它不会退化,因此可以获得良好的逆矩阵。 我们将收到伪逆。 这是她的看法。

现在,您可以获得从对到绝对的完整逆变换矩阵。 为此,我们将从对到分量的变换矩阵乘以从分量到绝对值的逆变换矩阵。 她看起来像这样。

尽管我们已经在上面看到了类似的内容,但是矩阵仍然不同。 我们检查它给出的结果。 我们将计算绝对路线,并已从中恢复配对。 恢复错误如下。

在除两个之外的所有对上,几乎为零的错误。 我们找出这些对有什么问题。
事实证明,在两个货币对中,接受了错误的数据。 对于jpy / hkd和jpy / sek,数据以10000和100件为单位。 必须纠正并重新检查。
纠正输入对路线(摆脱很多)并重新计算绝对路线和恢复的路线后,我们看一下恢复误差。

误差在0.3%以内。 错误程度可以接受。
这是绝对路线图的示例。
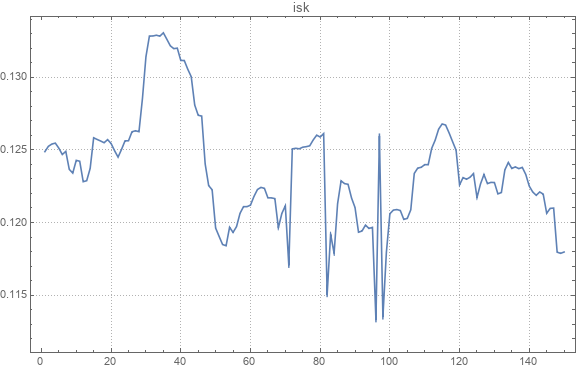
这是原始和恢复的对汇率的示例。

由于我们已经重新计算了逆变换的新矩阵,因此我们再次提供有关所有参与货币的最新绝对汇率的数据。
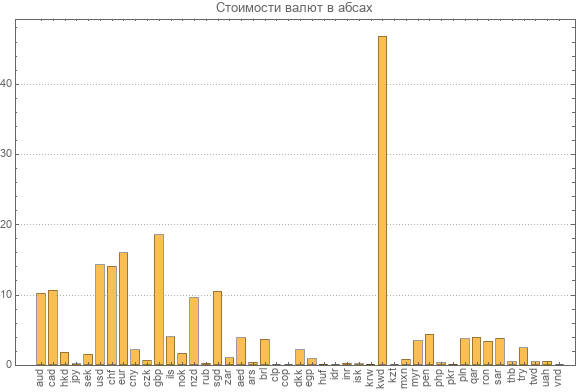
您会看到最昂贵的货币。 这是科威特第纳尔,价值近47腹肌。 越南盾的最小绝对值为0.003 abs。
结论
研究的结果表明,现有的绝对率计算方法存在很大的误差。 另外,在源数据中检测到错误。
从对到绝对值的逆变换矩阵只能通过使用具有非退化变换矩阵的较少线性独立分量的变换方法来获得。
获得逆变换矩阵的方法不使用成对速率数据。 因此独立于他们。
真实课程的转换验证显示出较低的错误率。 从中得出的结论是,找到的逆变换矩阵适用于成对的汇率到绝对汇率。
该方法并未声称已完成并经过数学验证,但是作为一种可接受的解决方案,它将用于进一步研究其绝对汇率。