Optlib 遗传优化算法在Rust中的实现

本文介绍了optlib库，该库旨在解决Rust语言中的全局优化问题。 在撰写本文时，该库实现了一种遗传算法，用于查找函数的全局最小值。 optlib库未绑定到用于优化功能的特定输入类型。 而且，库的构建方式使得在使用遗传算法时，可以轻松更改遗传算法的杂交，变异，选择和其他阶段的算法。 实际上，遗传算法就像是从立方体组装而成的。

全局优化问题

通常将优化问题表述如下。

对于某些给定的函数f （ x ），在x的所有可能值中，找到一个值x'，以使f （x'）取最小值（或最大值）。 而且， x可以属于各种集合-自然数，实数，复数，向量或矩阵。

函数f （ x ）的极值表示点x' ，函数f （ x ）的导数等于零。

有很多算法可以保证找到函数的极值，这是在给定起点x ₀附近的局部最小值或最大值。 这样的算法包括例如梯度下降算法。 但是，实际上，通常需要找到在给定的x范围内，除一个全局极值之外，还有许多局部极值的函数的全局最小值（或最大值）。

梯度算法无法解决此类功能的优化问题，因为它们的解收敛于起始点附近的最近极值。 对于发现全局最大值或最小值的问题，使用所谓的全局优化算法。 这些算法不能保证找到全局极值，因为 是概率算法，但别无选择，只能针对特定任务尝试使用不同的算法，看看哪种算法更好地应对优化，最好在最短的时间内以最大的概率找到全局极值。

遗传算法是最著名（且难以实现）的算法之一。

遗传算法的一般方案

遗传算法的思想逐渐产生，并在1960年代末-1970年代初形成。 在约翰·霍兰德（John Holland）的著作《自然和人工系统的适应》（1975）发行后，遗传算法得到了强大的发展。

遗传算法基于对大量世代中的个体群体进行建模。 在遗传算法的过程中，出现了具有最佳参数的新个体，而最不成功的个体死亡。 为了确定起见，以下是遗传算法中使用的术语。

• 个体是可能值集合中x的一个值，以及给定点x的目标函数的值。
• 染色体-x的值。
• 染色体-如果x是向量，则x _i的值。
• 适应度函数（适应度函数，目标函数）是优化函数f （ x ）。
• 人口是个人的集合。
• 生成-遗传算法的迭代次数。

每个人代表所有可能解的集合中x的一个值。 针对x的每个值计算优化函数的值（为简便起见，在将来，我们假设我们正在寻找函数的最小值）。 我们假设目标函数的重要性越小，该解决方案越好。

遗传算法被用于许多领域。 例如，它们可用于选择神经网络中的权重。 许多CAD系统使用遗传算法来优化设备参数以满足指定要求。 同样，可以使用全局优化算法来选择板上的导体和元件的位置。

遗传算法的结构图如下图所示：

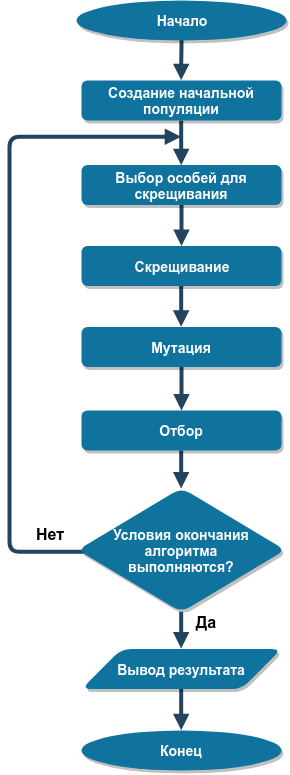
我们将更详细地考虑算法的每个阶段。

创建初始种群

该算法的第一阶段是创建初始种群，即创建许多具有不同x染色体值的个体。 通常，初始种群是由具有随机染色体值的个体创建的，同时试图确保种群中的染色体值相对均匀地覆盖整个解决方案搜索区域，除非对全局极值可能位于的位置做出任何假设。

您可以创建染色体，以使x的初始值通过给定步骤均匀分布在整个搜索区域中，而不是随机地分布染色体，这取决于在此算法阶段将创建多少个人。

在此阶段创建的个体越多，该算法找到正确解的可能性就越大，并且随着初始种群数量的增加，通常，遗传算法需要进行的迭代次数（世代数）减少。 但是，随着人口规模的增加，需要在算法的后续阶段增加目标函数的计算量以及其他遗传运算的性能。 即，随着人口规模的增加，一代的计算时间增加。

原则上，在遗传算法的整个工作过程中，种群的大小不必保持恒定，通常随着世代数量的增加，种群的大小可以减小，因为 随着时间的流逝，越来越多的人将被放置在更接近所需解决方案的位置。 但是，通常人口规模保持大致恒定。

选择个体进行杂交

创建种群后，有必要确定哪些个体将参与杂交操作（请参阅下一段）。 此阶段有多种算法。 它们中最简单的方法是将每个个体进行杂交，但是在下一步中，您将不得不执行过多的杂交操作并计算目标函数的值。

最好给与更多成功染色体（具有最低目标功能值）的个体交配的机会，以及那些目标功能更多（更差）的个体丧失交配后代的能力。

因此，在此阶段，您需要创建成对的个人（如果更多的个人可以参与到交叉中，则不必是成对的），将在下一阶段对其进行交叉操作。

在这里您还可以应用各种算法。 例如，随机创建对。 或者，您可以按目标函数的值按升序对个人进行排序，并创建更靠近已排序列表开头的个人对（例如，来自列表前半部分，列表前三分之一的个人等）。这种方法不好，因为花费时间排序个人。

经常使用比赛方法。 当随机选择几个人担任每个交叉申请者的角色时，其中目标函数值最高的那个人将被发送到将来的一对。 即使在这里，也可以引入随机性元素，使目标函数值最差的个人“击败”目标函数值最好的个人的机会很小。 这样一来，您可以维持更多的异质种群，从而保护其免于退化，即 从所有个体具有近似相等的染色体值的情况出发，这相当于将算法拖延到一个极端，可能不是全局的。

此操作的结果将是要穿越的伙伴的列表。

杂种

杂交是一种遗传操作，可以创造具有新染色体值的新个体。 根据父母的染色体创建新的染色体。 大多数情况下，在与一组伴侣交配的过程中，会创造一个女儿，但从理论上讲，可以创造更多的孩子。

交叉算法也可以以各种方式实现。 如果染色体类型是个数，那么最简单的方法就是创建一个新染色体，作为父母染色体的算术平均值或几何平均值。 对于许多任务来说这已经足够了，但是最常见的是使用其他基于位运算的算法。

按位交叉的工作方式使子染色体由一个父体的一部分位和另一父体的一部分位组成，如下图所示：

父分割点通常是随机选择的。 不必创建两个带有这种十字架的孩子，通常仅限于其中一个。

如果亲本染色体的分裂点为1，则这种杂交称为单点。 但是，当将亲本染色体分为几个部分时，也可以使用多点拆分，如下图所示：

在这种情况下，子染色体的更多组合是可能的。

如果染色体是浮点数，则可以将上述所有方法应用于它们，但是它们并不是非常有效。 例如，如前所述，如果将浮点数一点一点地相交，则许多相交操作将创建子染色体，该子染色体仅在最远的小数位处与父染色体之一不同。 使用双精度浮点数时，情况尤其恶化。

为了解决此问题，有必要回顾一下，按照IEEE 754标准的浮点数存储为三个整数：S（一位），M和N，根据它们计算出的浮点数为x =（-1） ^S × M× ^2N。 交叉浮点数的一种方法是，首先将数字划分为整数的分量S，M，N，然后对数字M和N进行上述按位交叉运算，然后选择其中一个的符号S父母，并从获得的值中做出一个女儿染色体。

在许多问题中，一个人没有一条，而是几条染色体，甚至可以是不同的类型（整数和浮点数）。 然后，还有更多选择可以穿越这些染色体。 例如，当创建一个女儿个体时，您可以穿越父母的所有染色体，或者可以完全改变父母之一的某些染色体而无需进行任何更改。

变异

突变是遗传算法的重要阶段，支持单个染色体的多样性，因此减少了解决方案将迅速收敛到某个局部最小值而不是全局最小值的机会。 突变是刚刚通过杂交而产生的个体染色体的随机变化。

通常，不会将突变的可能性设置得很高，以使该突变不会干扰算法的收敛，否则会破坏具有成功染色体的个体。

除了杂交之外，可以使用不同的算法进行突变。 例如，您可以用一个随机值替换一个或多个染色体。 但最常见的是，当染色体（或几个染色体）中的一个或几个位反转时，会使用按位突变，如下图所示。

一位突变：

几位突变：

突变的位数可以是预定义的，也可以是随机变量。

作为突变的结果，个体可能会变得更加成功和不那么成功，但是此操作可以使成功的染色体具有一组零和那些父母个体不必以非零概率出现的染色体。

选拔

由于杂交和随后的突变，出现了新个体。 如果没有选择阶段，那么个体数量将成倍增长，这将为每一代新一代人口提供越来越多的RAM和处理时间。 因此，在出现新个体之后，有必要清除最不成功个体的群体。 这是在选择阶段发生的事情。

选择算法也可以不同。 通常，首先将染色体不在解决方案搜索的给定间隔内的个体丢弃。

然后，您可以丢弃尽可能多的最不成功的人，以维持恒定的人口规模。 也可以应用各种概率选择标准，例如，选择一个人的概率可能取决于目标函数的值。

算法结束条件

与遗传算法的其他阶段一样，有几种准则可以终止算法。

结束算法的最简单标准是在给定的迭代（生成）次数后终止算法。 但是必须谨慎使用该标准，因为遗传算法具有概率性，并且算法的不同开始可以以不同的速度收敛。 通常，如果算法在大量迭代过程中找不到解决方案，则将迭代次数终止准则用作附加准则。 因此，必须将足够大的数字设置为迭代次数的阈值。

另一个停止标准是，如果对于给定的迭代次数没有出现新的最佳解决方案，则该算法将被中断。 这意味着该算法已找到全局极值或卡在局部极值中。

当所有个体的染色体具有相同的含义时，也存在不利的情况。 这就是所谓的简并人口。 在这种情况下，最有可能的是，算法陷入了一个极端，不一定是全局的。 只有成功的突变才能使种群摆脱这种状态，但由于通常将突变的可能性确定为很小，而且与突变将创造出更成功的个体的事实相距甚远，因此种群退化的情况通常被视为阻止遗传算法的借口。 为了检查该标准，有必要比较所有个体的染色体，它们之间是否存在差异，如果没有差异，则停止算法。

在某些问题中，没有必要找到一个全局最小值，而是找到一个好的解决方案，即目标函数的值小于给定值的解决方案。 在这种情况下，如果在下一次迭代中找到的解满足此标准，则可以提前停止算法。

optlib

Optlib是用于Rust语言的库，旨在优化功能。 在编写这些行时，库中仅实现了遗传算法，但将来计划通过向其添加新的优化算法来扩展该库。 Optlib完全用Rust编写。

Optlib是根据MIT许可分发的开源库。

• github上的页面-https: //github.com/Jenyay/rust-optimization
• 在crates.io上的页面-https://crates.io/crates/optlib
• 文档-https: //docs.rs/optlib

optlib ::基因

从遗传算法的描述可以看出，算法的许多阶段可以用不同的方式实现，选择它们，以便对于给定的目标函数，算法可以在最短的时间内收敛到正确的解。

optlib ::遗传模块的设计方式使得可以“从多维数据集”组装遗传算法。 在创建遗传算法将在其中进行工作的结构实例时，您需要指定将使用哪些算法来创建种群，选择配对对象，杂交，变异，选择以及使用什么标准来中断算法。

该库已经具有用于遗传算法各个阶段的最常用算法，但是您可以创建自己的类型来实现相应的算法。

在文库中，染色体是小数（即小数）向量的情况。 当函数f （ x ）最小时，其中x是浮点数（ f32或f64 ）的向量。

使用optlib :: Genetic的优化示例

在我们开始详细描述遗传模块之前，请考虑一个示例以最小化Schwefel函数。 此多维函数的计算公式如下：

$$

$$F（\粗体符号x）= 418.9829N-\ sum_ {i = 1} ^ {N} x_i \ sin（\ sqrt {| x_i |}）$$

在-500 <= x _i <= 500范围内的最小Schweffel函数位于点x' ，其中对于i = 1，2，...，N，所有x _i = 420.9687，该点的函数值为f（ x' ） = 0。

如果N = 2，则此函数的三维图像如下：

如果我们构建此功能的水平线，则更容易看到极端：

以下示例显示了如何使用遗传模块查找最小Schweffel函数。 您可以在examples / generic-schwefel文件夹的源代码中找到此示例。

//!    . //! //! y = f(x),  x = (x0, x1, ..., xi,... xn). //!      x' = (420.9687, 420.9687, ...) //!      xi - [-500.0; 500.0]. //! f(x') = 0 //! //! #  //! * ` ` -   . y = f(x). //! * `` -    , x = (x0, x1, x2, ..., xn). //! * `` -   x    . //! * `` -  . //! * `` -    . use optlib::genetic; use optlib::genetic::creation; use optlib::genetic::cross; use optlib::genetic::goal; use optlib::genetic::logging; use optlib::genetic::mutation; use optlib::genetic::pairing; use optlib::genetic::pre_birth; use optlib::genetic::selection; use optlib::genetic::stopchecker; use optlib::testfunctions; use optlib::Optimizer; ///    type Gene = f32; ///   type Chromosomes = Vec<Gene>; fn main() { //   //  .  xi     [-500.0; 500.0] let minval: Gene = -500.0; let maxval: Gene = 500.0; //      let population_size = 500; //   xi  . //  15-   let chromo_count = 15; let intervals = vec![(minval, maxval); chromo_count]; //      ( ) //      optlib::testfunctions let goal = goal::GoalFromFunction::new(testfunctions::schwefel); //       . // RandomCreator       . let creator = creation::vec_float::RandomCreator::new(population_size, intervals.clone()); //        //     . let partners_count = 2; let families_count = population_size / 2; let rounds_count = 5; let pairing = pairing::Tournament::new(partners_count, families_count, rounds_count); //   //      , //   -     let single_cross = cross::FloatCrossExp::new(); let cross = cross::VecCrossAllGenes::new(Box::new(single_cross)); //    //    (     ). let mutation_probability = 15.0; let mutation_gene_count = 3; let single_mutation = mutation::BitwiseMutation::new(mutation_gene_count); let mutation = mutation::VecMutation::new(mutation_probability, Box::new(single_mutation)); // .       , //     . let pre_births: Vec<Box<genetic::PreBirth<Chromosomes>>> = vec![Box::new( pre_birth::vec_float::CheckChromoInterval::new(intervals.clone()), )]; //    //   ,       1e-4 //   3000  (). let stop_checker = stopchecker::CompositeAny::new(vec![ Box::new(stopchecker::Threshold::new(1e-4)), Box::new(stopchecker::MaxIterations::new(3000)), ]); //    .  -   . //        NaN  Inf. //    ,     . let selections: Vec<Box<dyn genetic::Selection<Chromosomes>>> = vec![ Box::new(selection::KillFitnessNaN::new()), Box::new(selection::LimitPopulation::new(population_size)), ]; //     . //       , //       . let loggers: Vec<Box<genetic::Logger<Chromosomes>>> = vec![ Box::new(logging::StdoutResultOnlyLogger::new(15)), Box::new(logging::TimeStdoutLogger::new()), ]; //     let mut optimizer = genetic::GeneticOptimizer::new( Box::new(goal), Box::new(stop_checker), Box::new(creator), Box::new(pairing), Box::new(cross), Box::new(mutation), selections, pre_births, loggers, ); //    optimizer.find_min(); } 

可以通过运行命令从源根目录运行此示例

 cargo run --bin genetic-schwefel --release 

结果应如下所示：

 Solution: 420.962615966796875 420.940093994140625 420.995391845703125 420.968505859375000 420.950866699218750 421.003784179687500 421.001281738281250 421.300537109375000 421.001708984375000 421.012603759765625 420.880493164062500 420.925079345703125 420.967559814453125 420.999237060546875 421.011505126953125 Goal: 0.015625000000000 Iterations count: 3000 Time elapsed: 2617 ms 

大部分示例代码都涉及遗传算法各个阶段的特征对象的创建。 正如本文开头所写，遗传算法的每个阶段都可以通过各种方式实现。 要使用optlib ::基因模块，您需要创建特征对象，以一种或另一种方式实现每个步骤。 然后将所有这些对象转移到GeneticOptimizer结构的构造函数中，在该构造函数中实现遗传算法。

GeneticOptimizer结构的find_min（）方法开始执行遗传算法。

基本类型和对象

optlib模块的基本特征

开发optlib库的目的是在将来添加新的优化算法，以便程序可以轻松地从一种优化算法切换到另一种优化算法，因此optlib模块包含Optimizer特性，其中包括一种方法- find_min（），在执行时运行优化算法。 这里的类型T是对象的类型，它是解搜索空间中的一个点。 例如，在上面的示例中，这是Vec <Gene>（其中Gene是f32的别名）。 也就是说，这种类型的对象被馈送到目标函数的输入。

在optlib模块中声明了Optimizer特性，如下所示：

 pub trait Optimizer<T> { fn find_min(&mut self) -> Option<(&T, f64)>; } 

optim_ trait的find_min（）方法应该返回Option <（＆T，f64）>类型的对象，其中返回的元组中的＆T是找到的解决方案，f64是找到的解决方案的目标函数的值。 如果算法找不到解决方案，则find_min（）函数应返回None。

由于许多随机优化算法都使用所谓的代理（就遗传算法而言，代理是一个个体），因此optlib模块还包含带有单个get_agents（）方法的AlgorithmWithAgents特性，该方法应返回代理向量。

反过来，代理是一种实现optlib- Agent的另一个特征的结构。

特质AlgorithmWithAgents和Agent在optlib模块中声明如下：

 pub trait AlgorithmWithAgents<T> { type Agent: Agent<T>; fn get_agents(&self) -> Vec<&Self::Agent>; } pub trait Agent<T> { fn get_parameter(&self) -> &T; fn get_goal(&self) -> f64; } 

对于AlgorithmWithAgents和Agent，类型T的含义与对于Optimizer的含义相同，即，它是为其计算目标函数的值的对象的类型。

GeneticOptimizer结构-遗传算法实现

这两种类型都是针对GeneticOptimizer结构实现的-Optimizer和AlgorithmWithAgents。

遗传算法的每个阶段都由其自己的类型表示，可以从头开始实现，也可以使用内部可用的optlib ::基因实现之一。 对于遗传算法的每个阶段，在optlib ::遗传模块内部都有一个带有辅助结构和功能的子模块，这些子模块实现了遗传算法各阶段中最常用的算法。 关于这些模块将在下面讨论。 在这些子模块中的某些子模块中，还有一个vec_float子模块，用于实现从浮点数（f32或f64）的向量计算目标函数时的算法步骤。

GeneticOptimizer结构的构造函数声明如下：

 impl<T: Clone> GeneticOptimizer<T> { pub fn new( goal: Box<dyn Goal<T>>, stop_checker: Box<dyn StopChecker<T>>, creator: Box<dyn Creator<T>>, pairing: Box<dyn Pairing<T>>, cross: Box<dyn Cross<T>>, mutation: Box<dyn Mutation<T>>, selections: Vec<Box<dyn Selection<T>>>, pre_births: Vec<Box<dyn PreBirth<T>>>, loggers: Vec<Box<dyn Logger<T>>>, ) -> GeneticOptimizer<T> { ... } ... } 

GeneticOptimizer的构造函数接受许多类型的对象，这些对象会影响遗传算法的每个阶段以及结果的输出：

• 目标：框<dyn目标<T >>-目标函数；
• stop_checker：框<dyn StopChecker <T >>-停止条件；
• 创建者：Box <dyn Creator <T >>-创建初始人口；
• 配对：Box <dyn Pairing <T >>-选择交配伙伴的算法；
• cross：Box <dyn Cross <T >>-穿越算法;
• 变异：Box <dyn变异<T >>-变异算法;
• 选择：Vec <Box <dyn Selection <T> >>-选择算法的向量；
• pre_births：Vec <Box <dyn PreBirth <T> >>-一种在创建个体之前销毁不成功染色体的算法的载体；
• 记录器：Vec <Box <dyn Logger <T> >>-对象的向量，保留遗传算法的日志。

要运行该算法，必须执行Optimizer特性的find_min（）方法。 另外，GeneticOptimizer结构具有next_iterations（）方法，可在find_min（）方法完成后用于继续计算。

有时在停止算法后，更改算法参数或使用的方法很有用。 可以使用GeneticOptimizer结构的以下方法完成此操作：replace_pairing（），replace_cross（），replace_mutation（），replace_pre_birth（），replace_selection（），replace_stop_checker（）。 这些方法使您可以替换在创建GeneticOptimizer结构时传递给它的特征对象。

遗传算法的主要类型将在以下各节中讨论。

目标特质-目标功能

目标特征在optlib ::遗传模块中声明如下：

 pub trait Goal<T> { fn get(&self, chromosomes: &T) -> f64; } 

get（）方法应返回给定染色体的目标函数的值。

在optlib :: Genetic ::目标模块内部，有一个GoalFromFunction结构，该结构实现了Goal 特性 。 对于此结构，有一个采用函数的构造函数，这是目标函数。 也就是说，使用此结构，您可以从常规函数创建目标类型对象。

创作者特征-创建初始人口

创造者特​​征描述了初始种群的“创造者”。 此特征声明如下：

 pub trait Creator<T: Clone> { fn create(&mut self) -> Vec<T>; } 

create（）方法应返回染色体向量，并以此为基础创建初始种群。

对于优化多个浮点数的函数的情况， optlib :: Genetic :: Creator :: Vec_float模块具有RandomCreator <G>结构，用于以随机方式创建染色体的初始分布。

在下文中，类型<G>是染色体载体中一个染色体的类型（有时使用术语“基因”代替术语“染色体”）。 如果染色体是Vec <f32>或Vec <f64>类型，则<G>基本上表示f32或f64类型。

RandomCreator <G>的结构声明如下：

 pub struct RandomCreator<G: Clone + NumCast + PartialOrd> { ... } 

这里的NumCast是来自num crate的类型。 此类型允许您使用from（）方法从其他数字类型创建类型。

要创建RandomCreator <G>结构，您需要使用new（）函数，该函数声明如下：

 pub fn new(population_size: usize, intervals: Vec<(G, G)>) -> RandomCreator<G> { ... } 

在这里，种群大小是种群的大小（要创建的染色体组的数量），间隔是两个元素的元组的向量-染色体组中相应染色体（基因）的最小值和最大值，此向量的大小决定了该染色体组中包含多少个染色体每个人。

在上面的示例中，Schweffel函数针对f32类型的15个变量进行了优化。 每个变量必须在[-500; 500]。 也就是说，要创建总体，间隔向量必须包含15个元组（-500.0f32、500.0f32）。

类型配对-选择配对伙伴

配对特征用于选择要杂交的个体。 此特征声明如下：

 pub trait Pairing<T: Clone> { fn get_pairs(&mut self, population: &Population<T>) -> Vec<Vec<usize>>; } 

get_pairs（）方法使用一个指向“ 人口”结构的指针，该结构包含人口中的所有个体，通过该结构，您还可以找出人口中最好和最差的个体。

配对get_pairs（）方法应返回一个向量，该向量包含存储将要杂交的个体的索引的向量。 根据交叉算法（将在下一节中讨论），两个或更多个人可以交叉。

例如，如果具有索引0和10、5、2、6和3的个体被交叉，则get_pairs（）方法应返回向量vec！[Vec！[0，10]，vec！[5，2]，vec！[ 6，3]]。

optlib ::遗传::配对模块包含两个结构，可实现各种伙伴选择算法。

对于RandomPairing结构，配对类型的实现方式是随机选择伙伴进行交配 。

对于锦标赛结构，配对特征以使用锦标赛方法的方式实现。 锦标赛方法意味着将要参加十字架的每个人都必须击败另一个人（获胜个人的目标函数的值必须较小）。 如果锦标赛方法使用一轮，则意味着随机选择了两个人，并且这两个人中目标函数值较低的一个人进入了未来的“家庭”。 如果使用多个回合，则以这种方式获胜的个人应与几个随机的个人获胜。

Tournament结构的构造函数声明如下：

 pub fn new(partners_count: usize, families_count: usize, rounds_count: usize) -> Tournament { ... } 

在这里：

• partners_count-穿越所需的个人人数；
• family_count-“家庭”数，即 将产生后代的个体的集合；
• rounds_count-比赛中的回合数。

作为对锦标赛方法的进一步修改，您可以使用随机数生成器，以很小的机会击败目标函数值最差的个人，即 为了使获胜概率受目标函数值的影响，并且两个竞争对手之间的差异越大，获胜最佳个人的机会就越大，并且在目标函数值几乎相等的情况下，一个人获胜的可能性将接近50％。

交叉类型

个体的“家庭”形成后，为了杂交，您需要杂交他们的染色体才能使孩子拥有新的染色体。 Cross阶段由Cross类型表示，声明如下：

 pub trait Cross<T: Clone> { fn cross(&mut self, parents: &[&T]) -> Vec<T>; } 

cross（）方法跨一组父母。 该方法接受父母参数（来自对父母（而不是个人本身）染色体的切片），并应返回新染色体的向量。 父母的大小取决于使用配对特征选择配对对象的算法，该算法已在上一节中进行了描述。 通常使用一种算法，该算法基于两个亲本的染色体创建新的染色体，然后亲本的大小将等于两个。

optlib :: Genetic :: cross模块包含使用不同的cross算法实现Cross类型的结构。

• VecCrossAllGenes-一种用于跨染色体的结构，当每个人都有一组染色体时-这是一个向量。 VecCrossAllGenes构造函数接受Cross对象类型，该类型将应用于父染色体向量的所有元素。 在这种情况下，亲本染色体载体的大小必须相同。 上面的示例使用VecCrossAllGenes结构，因为使用的个体中的染色体是Vec <f32>类型。
• CrossMean是一种以两个数相交的结构，以作为子染色体，将有一个作为母体染色体的算术平均值计算出的数字。
• FloatCrossGeometricMean是一个以两个数相交的结构，以作为子染色体，将有一个作为母染色体的几何平均值计算出的数。 应该有浮点数作为染色体。
• CrossBitwise-两个数字的按位单点交叉。
• FloatCrossExp-浮点数的按位单点交叉。 尾数与父母参展商相互交叉。 孩子从一位父母那里收到了手势。

optlib :: Genetic :: cross模块还包含用于对不同类型的数字（整数和浮点数）进行按位交叉的函数。

类型突变-突变

杂交后，有必要对获得的孩子进行突变，以保持染色体的多样性，并且种群没有滑落到简并状态。 对于人群，特质是突变的 ，声明如下：

 pub trait Mutation<T: Clone> { fn mutation(&mut self, chromosomes: &T) -> T; } 

突变性状的唯一mutation（）方法引用了一条染色体，并且应该返回一个可能发生了改变的染色体。 通常，建立突变的可能性很小，例如百分之几，因此仍然保留了在亲本的基础上获得的染色体，从而提高了种群。

optlib :: Genetic ::突变模块中已经实现了一些突变算法。

例如，此模块包含VecMutation结构，该结构与VecCrossAllGenes结构类似，即 如果染色体是向量，则VecMutation接受Mutation对象类型，并以给定的概率将其应用于向量的所有元素，从而创建具有突变基因（染色体向量的元素）的新向量。

optlib :: genetic :: mutation模块还包含一个实现了Mutation 特性的BitwiseMutation结构。 这种结构可以反转染色体中给定数目的随机位数。 建议将此结构与VecMutation结构一起使用。

出生前特征-预选

杂交和变异后，通常会发生选择阶段，最失败的个体将被摧毁。 但是，在optlib ::遗传库中实施遗传算法时，在选择步骤之前，还有另一个步骤可以丢弃不成功的染色体。 添加此步骤的原因是，针对个人的目标函数的计算通常会花费大量时间，并且如果染色体未落入已知搜索间隔，则无需进行计算。 例如，在上面的示例中，染色体不落在段[-500; 500]。

要执行此类预过滤，必须使用PreBirth特质 ，该特质声明如下：

 pub trait PreBirth<T: Clone> { fn pre_birth(&mut self, population: &Population<T>, new_chromosomes: &mut Vec<T>); } 

PreBirth性状的唯一preBirth（）方法是对上述种群结构的引用，也是对new_chromosomes染色体向量的可变引用。 这是突变步骤后获得的染色体载体。 pre_birth（）方法的实现应从该向量中删除显然不适合该问题条件的那些染色体。

对于优化浮点数矢量的功能的情况， optlib :: Genetic :: pre_birth :: vec_float模块包含CheckChromoInterval结构，该结构旨在删除染色体（如果它们是浮点数矢量）以及该矢量的某些元素不属于指定的时间间隔。

CheckChromoInterval结构的构造函数如下：

 pub fn new(intervals: Vec<(G, G)>) -> CheckChromoInterval<G> { ... } 

在这里，构造函数采用具有两个元素的元组向量-染色体中每个元素的最小值和最大值。 因此，间隔向量的大小必须与个体的染色体向量的大小一致。 在上面的示例中，使用15个元组（-500.0f32、500.0f32）的向量作为间隔。

选择选择-选择

初步选择染色体后，将创建个体并将其放置在种群中（ 种群结构）。 在为每个人创建个人的过程中，将计算目标函数的值。 在选择阶段，一定数量的个体必须被销毁，以使种群不会无限期地增长。 为此，使用选择特征，其声明如下：

 pub trait Selection<T: Clone> { fn kill(&mut self, population: &mut Population<T>); } 

在kill（）方法中实现Selection特质的对象必须为需要销毁的种群中的每个个体调用Individual结构（个体）的kill（）方法。

要绕过人口中的所有个人，可以使用返回人口结构的IterMut（）方法的迭代器。

由于通常必须应用几个选择条件，因此在创建GeneticOptimizer结构时，构造函数接受选择类型对象的向量。

与遗传算法的其他阶段一样， optlib :: Genetic ::选择模块已经提供了选择阶段的几种实现。

• KillFitnessNaN-销毁目标函数值为NaN或Inf的个人。
• LimitPopulation-销毁这么多最坏的个体，使人口规模不超过给定规模。
• optlib ::遗传::选择:: vec_float :: CheckChromoInterval-如果优化了浮点数向量的功能，则会破坏其染色体值不适合给定间隔的个体。 该结构的工作方式与遗传算法前一阶段的optlib :: Genetic :: pre_birth :: vec_floatCheckChromoInterval结构相似。

StopChecker特性-停止条件

在选择阶段之后，您需要检查是否应该停止遗传算法。 如上所述，在此阶段，您还可以使用各种停止算法。 对于算法的中断，对象负责实现StopChecker特性 ，该特性声明如下：

 pub trait StopChecker<T: Clone> { fn can_stop(&mut self, population: &Population<T>) -> bool; } 

如果可以停止算法，则can_stop（）方法应返回true，否则该方法应返回false。

optlib :: Genetic :: Stopchecker模块包含几个具有基本停止条件的结构，以及两个用于从其他条件创建组合的结构：

• MaxIterations-按世代号中断标准。 遗传算法将在给定数量的迭代（生成）后停止。
• GoalNotChange-中断标准，如果对于给定的迭代次数找不到新的解决方案，则算法应根据该标准停止运行。 换句话说，如果对于给定的世代数，没有更多的成功个体出现。
• 阈值 -一种停止标准，如果当前最佳解决方案的目标函数的值小于指定的阈值，则遗传算法将被中断。
• CompositeAll — , ( - StopChecker). , - , .
• CompositeAny — , ( - StopChecker). , - , .

Logger —

Logger , , , . Logger :

 pub trait Logger<T: Clone> { ///       fn start(&mut self, _population: &Population<T>) {} ///     , ///           fn resume(&mut self, _population: &Population<T>) {} ///         /// (    ) fn next_iteration(&mut self, _population: &Population<T>) {} ///      fn finish(&mut self, _population: &Population<T>) {} } 

optlib::genetic::logging , Logger:

• StdoutResultOnlyLogger — ;
• VerboseStdoutLogger — .
• TimeStdoutLogger — , .

作为最后一个参数，GeneticOptimizer结构的构造函数接受Logger 特征 -objects的向量，这使您可以灵活地配置程序的输出。

测试优化算法的功能

Schweffel函数

为了测试优化算法，发明了许多具有许多局部极值的功能。模块optlib :: testfunctions包含几个功能，其可以被测试的算法。在撰写本文时，optlib :: testfunctions模块仅包含两个函数。

这些功能之一是Schweffel函数，该函数在本文的开头就进行了介绍。再一次，我记得该函数编写如下：

$$

$$F(\boldsymbol x) = 418.9829N - \sum_{i=1}^{N}x_i \sin (\sqrt{|x_i|})$$

x' = (420.9687, 420.9687, ...). .

optlib::testfunctions schwefel . N .

, , , , .

:

$$

$$F(\boldsymbol x) = \sum_{i=1}^{N} (x_i - n)^2$$

x' = (1.0, 2.0,… N). .

optlib::testfunctions paraboloid .

结论

optlib , . ( optlib::genetic ), , , , .

optlib::genetic. . , , , , .

, . , ( , ..)

此外，计划添加新的分析功能（除Schweffel函数外）以测试优化算法。

我再次回忆起与optlib库相关的链接：

• github上的页面-https: //github.com/Jenyay/rust-optimization
• 页面上crates.io - https://crates.io/crates/optlib
• 文档-https: //docs.rs/optlib

我期待您的评论，补充和评论。