我们将从本周开始的有用资料开始,专门介绍
“开发人员算法”课程。 好好阅读。
 1.概述
1.概述散列是一种很好的实用工具,具有有趣而精妙的理论。 除了将数据用作词汇结构外,在许多不同领域也发现了哈希,包括密码学和复杂性理论。 在本讲座中,我们将描述两个重要的概念:通用哈希(也称为通用哈希函数家族)和理想哈希。
本讲座重点介绍的材料包括:
2.简介我们将考虑之前讨论的字典的主要问题,并考虑两个版本:静态和动态:
- 静态的 :给定很多S元素,我们希望以一种可以快速执行搜索的方式来存储它。
- 例如,固定字典。
- 动态的 :这里我们有一系列插入,搜索和可能的删除请求。 我们希望有效地完成所有这些工作。
对于第一个问题,我们可以使用排序数组和二进制搜索。 第二,我们可以使用平衡的搜索树。 但是,哈希提供了一种替代方法,通常是解决这些问题的最快,最方便的方法。 例如,假设您正在编写一个用于AI搜索的程序,并且想要存储已经解决的情况(电路板上的位置或状态空间的元素),以便在再次遇到它们时不再重复相同的计算。 散列提供了一种存储此信息的简便方法。 在密码学,网络,复杂性理论中也有许多应用。
3.哈希基础哈希的正式设置如下。
- 这些键属于某个较大的U集(例如,假设U是所有字符串的集合,最大长度为80个ascii字符。)
- U中确实需要一些S键(键可以是静态的也可以是动态的)。 令N = | S |。 想象一下,N比U的大小小得多。例如,S是班级中比128 ^ 80小得多的学生姓名的集合。
- 我们将使用大小为M的数组A和哈希函数 h进行插入和搜索:U→{0,...,M-1}。 给定元素x,哈希的思想是我们要将其存储在A [h(x)]中。 请注意,如果U小(例如2个字符的字符串),则可以像块排序一样将x保存到A [x]中。 问题在于U很大,因此我们需要一个哈希函数。
- 我们需要一种解决冲突的方法。 当两个不同的键x和y的h(x)= h(y)时发生冲突。 在本讲座中,我们将通过将A的每个元素定义为链接列表来处理冲突。 还有许多其他方法,但是对于我们将在此处关注的问题,这是最合适的。 该方法称为链接方法。 要插入项目,我们只需将其放在列表顶部。 如果h是一个很好的哈希函数,那么我们希望列表会很小。
哈希的一大优点是所有字典操作都非常容易实现。 要搜索键x,只需计算索引i = h(x),然后遍历A [i]中的列表,直到找到它为止(或退出列表)。 要插入,只需在列表顶部放置一个新项目即可。 要删除,您只需要在链表中执行删除操作。 现在我们来思考一个问题:要取得良好的性能我们需要什么?
理想的特性。 良好的哈希方案的关键期望的属性:
- 键分散得很好,因此我们不会发生太多冲突,因为冲突会影响搜索和删除时间。
- M = O(N):尤其是,我们希望电路实现特性(1),而表M的大小不必比元素N的数目大得多。
- 函数h必须快速计算。 在今天的分析中,我们将考虑将h(x)计算为常数的时间。 但是,值得记住的是,它不应该太复杂,因为它会影响整个执行时间。
鉴于此,元素x的搜索时间为O(列表的大小为A [h(x)])。 删除也是如此。 无论列表的长度如何,插入都需要O(1)时间。 因此,我们要分析这些列表的大小。
基本直觉:精美分配元素的一种方法是随机分配元素。 不幸的是,我们不能仅使用随机数生成器来决定将下一个元素定向到哪里,因为那样我们再也找不到它了。 因此,从某种形式上讲,我们希望h成为“伪随机”。
现在,我们将介绍一些坏消息,然后是一些好消息。
语句1(坏消息)对于任何哈希函数h,如果| U | ≥(N -1)M +1,存在N个元素的集合S,所有元素散列在一个位置。
证明:通过狄利克雷原理。 特别是要考虑对点,如果每个位置都具有不超过N-1个元素(对其进行散列),则U的大小不超过M(N-1)。
这就是为什么散列看起来如此神秘的部分原因-如果对于任何散列函数,您都可以想到防止散列的方法,那么如何辩称散列是好的呢? 一个答案是,有很多简单的哈希函数在典型的S集上都可以很好地工作,但是如果我们想对最坏的情况做出好的保证,该怎么办?
这是关键思想:让我们在h构造中使用随机化,类似于随机化的快速排序。 (不用说,h将是确定性函数)。 我们将证明,对于任何插入和搜索操作序列(我们不需要假定插入元素S的集合是随机的),如果我们以这种概率方式选择h,则该h在此序列中的性能会很好。 因此,这与随机快速分类或陷阱中的保证相同。 特别是,这就是通用哈希的想法。
一旦提出了这个想法,我们将把它用于一个特别有趣的应用程序,称为“完美哈希”。
4.通用哈希定义1.用于构造哈希函数h的随机算法H:U→{1,...,M}
如果所有x!= y在U中都是通用的
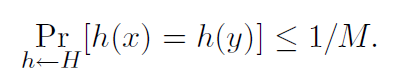
我们也可以说,如果“随机选择h∈H”过程是通用的,则哈希函数的集合H是哈希函数的通用族。 (在这里,我们确定了一组函数,并且在该函数集上具有均匀的分布。)
定理2。如果H是普适的,则对于任何大小为N的集合S⊆U,对于任何x∈U(例如,我们可以寻找),如果我们根据H随机构造h,则x与其他物体之间的预期碰撞次数S中的元素不超过N / M。
证明:根据“通用”的定义,每个y∈S(y!= X)最多有1 / M与x发生碰撞的机会。 所以
- 如果x和y发生冲突,则令Cxy = 1,否则为0。
- 令Cx表示x的碰撞总数。 因此,Cx =Py∈S,y!= X Cxy。
- 我们知道E [Cxy] = Pr(x和y碰撞)≤1 /M。
- 因此,在期望线性中,E [Cx] = Py E [Cxy] <N /M。
现在我们得到以下推论。
推论3。如果H是通用的,那么对于任何一次插入,搜索和删除操作L的序列(一次在一个系统中最多只能有M个元素),随机h∈H的L个操作的预期总成本仅为O(L)(查看时间)将h计算为常数)。
证明:对于序列中的任何给定运算,其期望成本由定理2恒定,因此L运算的期望总成本在期望线性上为O(L)。
问题:我们实际上可以构建通用H吗? 如果没有,那么这一切都是毫无意义的。 幸运的是,答案是肯定的。
4.1。 创建通用哈希族:矩阵方法假设密钥长度为u位。 假设表M的大小等于2度;因此,索引为b位长,M = 2b。
我们要做的是选择h作为0/1 b-by-u的随机矩阵,并定义h(x)= hx,在其中添加mod2。这些矩阵又短又厚。 例如:
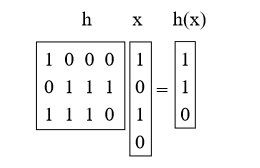
命题4。对于x!= Y Prh [h(x)= h(y)] = 1 / M = 1 / 2b。
证明:首先,将h乘以x是什么意思? 我们可以将其视为添加一些列h(执行矢量加法模2),其中x中的1位表示要添加的列。 (例如,我们在上面添加了h的第一列和第三列)
现在取一个任意的密钥对x,y,使x!=Y。 它们在某处必须不同,以使它们的第i个坐标不同,并且为具体起见,我们说xi = 0和yi =1。想象一下,我们首先选择了除第i列以外的所有h。 对于第i列的其余样本,h(x)是固定的。 但是,第i列的2b个不同设置中的每一个都会给出不同的h(y)值(特别是,每次我们在此列中旋转一位时,都会将相应的位转换为h(y))。 因此,h(x)= h(y)恰好有1 / 2b的机会。
还有其他构造通用哈希族的方法,这些方法也基于素数的乘法(请参见第6.1节)。
我们将考虑的下一个问题:如果纠正集合S,是否可以找到一个哈希函数h,使所有搜索都具有恒定的时间? 答案是肯定的,这引出了完美哈希的主题。
5.完美的哈希我们说,如果所有搜索都在O(1)中进行,那么散列函数对于S是理想的。 这是为给定集合S构建完善的哈希函数的两种方法。
5.1方法1:空间O(N2)中的解假设我们想要一个表,其大小是字典S的大小N的平方。然后,这是一种构造理想哈希函数的简单方法。 令H为通用且M = N2。 然后从H中随机选择一个h并尝试! 声明说,她至少有50%的机会不会发生碰撞。
命题5。如果H是通用的且M = N2,则Prh〜H(S中无碰撞)≥1/2。
证明:
•S中有几对(x,y)? 答案是:

•对于每一对,根据通用性的定义,它们发生碰撞的概率≤1 /M。
•因此Pr(有碰撞)≤

/ M <1/2。
这就像“生日悖论”的另一面。 如果天数比平方数大得多,则很可能没有一对夫妇有相同的生日。
因此,我们只是从H中选择一个随机的h,如果发生任何冲突,我们只需选择一个新的h。 平均而言,我们只需要这样做两次。 现在,如果我们只想使用O(N)空间怎么办?
5.2方法2:空间O(N)中的解
关于是否可以在O(N)空间中实现完美哈希的问题已经存在了一段时间:“是否应该对表进行排序?” 也就是说,对于固定集,仅线性空间可以获得恒定的搜索时间? 进行了一系列越来越复杂的尝试,直到最终使用两级方案中的通用哈希函数的好主意将其解决。
方法如下。 首先,我们将使用通用哈希将其哈希到大小为N的表中。 这将导致一些碰撞(除非我们很幸运)。 但是,然后我们使用方法1重新哈希每个篮子,对篮子的大小进行平方以得到零碰撞。 因此,该方案包括以下事实:我们具有第一级h的哈希函数和第一级的表A,然后具有第二级A1,...,hN和N的第二级的表H1,...,hN和N的N个哈希函数。为了找到元素x,我们首先计算i = h(x),然后在Ai [hi(x)]中找到元素。 (如果您在实践中这样做,则可以设置标志,以便仅在与索引i确实存在冲突时才采取第二步,否则,您只需将x本身放在A [i]中,但让我们让我们不必为此担心。)
假设哈希函数h将S的n个元素哈希到位置i。 我们已经证明(通过分析方法1),我们可以找到h1,...,hN,因此辅助表中使用的总空间为Pi(ni)2。这仍然表明我们可以找到一个第一级函数h使得Pi(ni)2 = O(N)。 实际上,我们将显示以下内容:
定理6.如果我们从通用集合H中选择起点h,则
Pr[X i (ni)2 > 4N] < 1/2.
证明。 让我们证明E [Pi(ni)2] <2N。 这意味着我们要从马尔可夫不等式中得到什么。 (如果总和可能大于4N的概率甚至是1/2,那么仅此事实就意味着期望值应大于2N。因此,如果期望值小于2N,则失败的可能性应该较小1/2)。
现在,棘手的技巧是,计算此数量的一种方法是计算发生冲突(包括与自身的冲突)的有序对的数量。 例如,如果购物篮具有{d,e,f},则d将与{d,e,f}中的每个冲突,e将与{d,e,f}中的每个冲突,并且f将与以下两个冲突{d,e,f}的每一个,所以我们得到9。因此,我们有:
E[X i (ni)2] = E[X x X y Cxy] (Cxy = 1 if x and y collide, else Cxy = 0) = N +X x X y6=x E[Cxy] ≤ N + N(N − 1)/M (where the 1/M comes from the definition of universal) < 2N. (since M = N)
因此,我们只是尝试从H随机选择一个h,直到找到一个使Pi n2 i <4N的值,然后固定此函数h,就可以像方法1那样找到N个二级哈希函数h1,...,hN。
6.进一步讨论6.1另一种通用哈希方法这是构造通用哈希函数的另一种方法,它比先前给出的矩阵方法稍微有效。
在矩阵方法中,我们将密钥视为位向量。 在这种方法中,我们将把键x视为整数[x1,x2,...,xk]的向量,唯一的要求是每个xi在{0,1,...,M-1}范围内。 例如,如果我们对长度为k的字符串进行哈希处理,则xi可以是第i个字符(如果表的大小至少为256)或第i个字符对(如果表的大小至少为65536)。 另外,我们将要求表M的大小为素数。 要选择哈希函数h,我们从{0,1,...,M-1}中选择k个随机数r1,r2,...,pk,并确定:
h(x) = r1x1 + r2x2 + . . . + rkxk mod M.
该方法具有通用性的证明与矩阵方法的证明相同。 令x和y为两个不同的键。 我们要证明Prh(h(x)= h(y))≤1 /M。由于x!= Y,因此应该存在这样的情况:存在某个索引i使得xi!= Yi。 现在假设您首先为j!= I选择了所有随机数rj。 令h'(x)= Pj6 = i rjxj。 因此,选择ri,我们得到h(x)= h'(x)+ rixi。 这意味着我们恰好在x和y之间存在冲突
h′(x) + rixi = h′(y) + riyi mod M, or equivalently when ri(xi − yi) = h′(y) − h′(x) mod M.
由于M为质数,除以mod M的一个非零值是有效的(从1到M -1的每个整数都具有一个乘积逆模M),这意味着存在一个等式ri模M的正值真,即ri =(h'(y)-h'(x))/(xi-yi)modM。因此,此事件的概率恰好是1 /M。
6.2哈希的其他用途假设我们有很长的元素序列,并且我们想看看列表中有多少个不同的元素。 有什么好方法吗?
一种方法是创建一个哈希表,然后通过搜索每个元素然后插入(如果尚未在表中插入)来遍历序列。 单个元素的数量就是插入数。
现在,如果列表确实很大并且我们没有存储空间的地方,但是大概的答案适合我们。 例如,假设我们是一台路由器,观察有多少个数据包通过,我们想(大约)看到有多少个不同的源IP地址。
这是一个好主意:假设我们有一个散列函数h的行为类似于随机函数,并且假设h(x)是从0到1的实数。我们可以做的一件事就是保持最小值到目前为止,哈希值已经产生(因此我们根本没有表格)。 例如,如果键是3,10,3,3,12,10,12且h(3)= 0.4,h(10)= 0.2,h(12)= 0.7,则得到0, 2。
事实是,如果我们在[0,1]中选择N个随机数,则期望的最小值将是1 /(N + 1)。 此外,它很有可能非常接近(我们可以通过运行多个哈希函数并取低点的中位数来提高估计值)。
问题:为什么要使用哈希函数,而不是每次都选择随机数? 这是因为我们关心的是不同元素的数量,而不仅仅是元素的总数(这个问题要简单得多:只需使用一个计数器...)。
朋友,这篇文章对您有帮助吗? 发表评论并参加将于4月25日举行的
开放日。