👩🏻‍🤝‍👨🏽 🙈 👩‍❤️‍💋‍👨 但是我们不向光通信挥手吗？激光，太空，CubeSat 👩🏿‍🚒 ⏸️ ⏭️

下述材料是作为当地课程项目（高级研究项目）的一部分与伊尔默瑙理工大学教师共同努力的结果。经验很有趣，但并非没有一定的困难。我们和当时的新娘一起完成了这个项目（还有一个）-是的，所以我们很幸运能一起学习并前往德国实习。实际上，是她在更大程度上完成了这部分工作，但我想推广这个话题。

因此，有一天我们约好选择科学工作的主题...

背景短（面部）

1号德语老师 ：哦，听说您在家学习CubeSat卫星？

我和我未来的妻子 ：恩，你可以这么说...

净重 1号：太好了！但是，如果您尝试考虑卫星之间的光通信怎么办？我知道在某些情况下光学器件可以提供最佳的能量性能，对于这样的小型卫星，我认为这个问题非常重要。我有一个专业从事无线光学的朋友。我认为这将是一个有趣的项目！

我们：听起来很有趣！

（过了一段时间）

与2号德语老师见面 。

净重 2号：是的，所有这一切当然很棒，但是什么样的卫星呢？这么小的质量？他们甚至可以交流吗？谁建议的？理解了……显然，我们不会在这些会议上见到他。去搜索真实的例子-我还不相信。

然后我们出发 ...

而且，令他们高兴的是，他们甚至找到了整篇有关该主题的文章。一个重要的区别是，通过光学设备进行的通信应该与地球进行通信，而不是与卫星之间进行通信。这非常重要，因为：

各种各样的散射和干扰，当然，在这种情况下，
但是，地球上的接收器可以设置得足够大，并且发射器非常准确。您知道，空间部分使事情变得有些复杂。

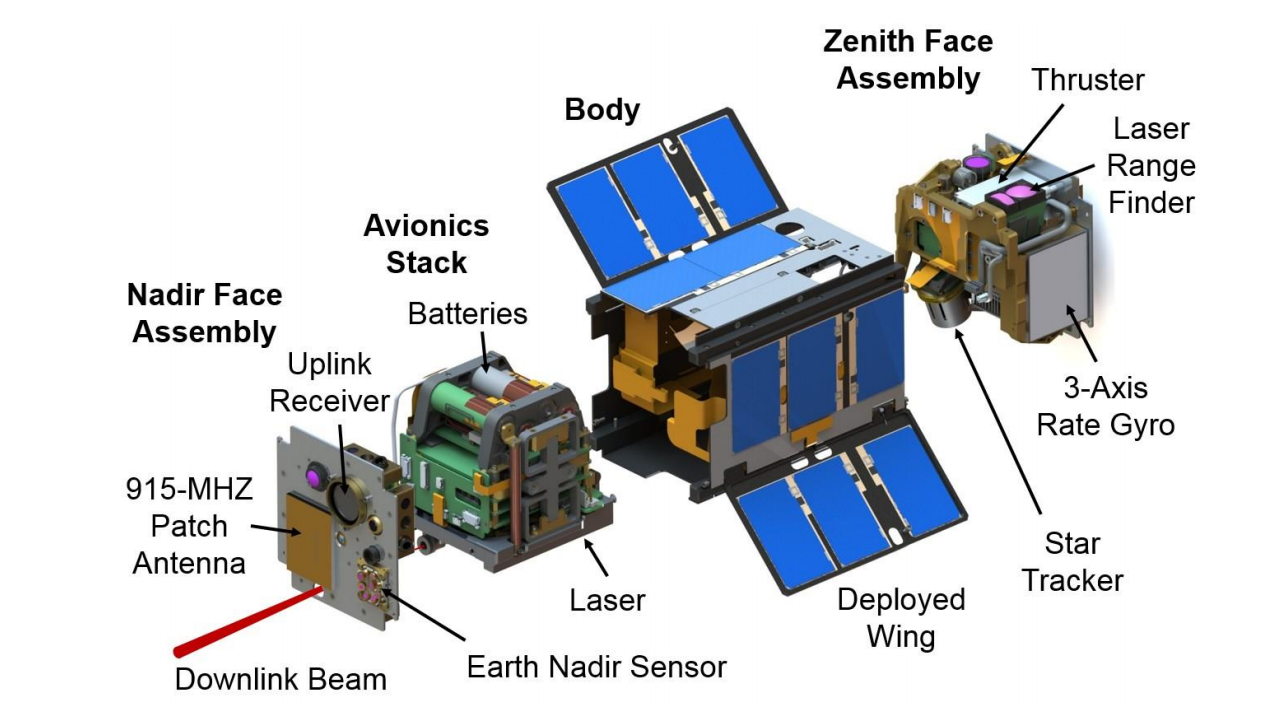
图 1. AeroCube-OCSD纳米卫星[1]的示意图。

但这已经是事情了，我们再次预约了。

净重 No. 2 ：好吧，好吧，因为NASA ...让我们尝试计算能量预算，并将其与无线电链路的能量预算进行比较。相关文章甩开？

他删除了自己的文章[2] （今天我将多次提及）和其他作者的几篇文章，以期对该问题有一个大致的了解。

卫星间光线路的能量预算意味着什么？

无线光能预算

但这通常暗示着自己与往常一样（必要的发射机功率，接收功率，SNR等）–仅噪声被认为比无线电通信更有趣...

让我们开始建模-这将变得更加清晰：

import numpy as np from matplotlib.pyplot import plot, grid, xlabel, ylabel, legend import matplotlib.pyplot as plt from scipy import special

假设我们有这样一个系统：

 #initial parameters for optical case R = 100*1e3 #distance between objects, eg satellites, in m (100 km) Bit_rate = 1e6 #bit rate (1 Mbps) h = 6.62607004*1e-34 # Planck constant c = 299792458 #speed of light wavelength_opt = 1550*1e-9 #optical wavelength freq_opt = c/wavelength_opt #optical frequency Ptx_opt = 1 #transmitter power in Watts Ptx_opt_dBm = 10*np.log10(Ptx_opt*1e3) #transmitter power in dBm

我们定义了一组可能的光接收器直径（实际上是透镜）-我们牢记对卫星自身大小的限制：

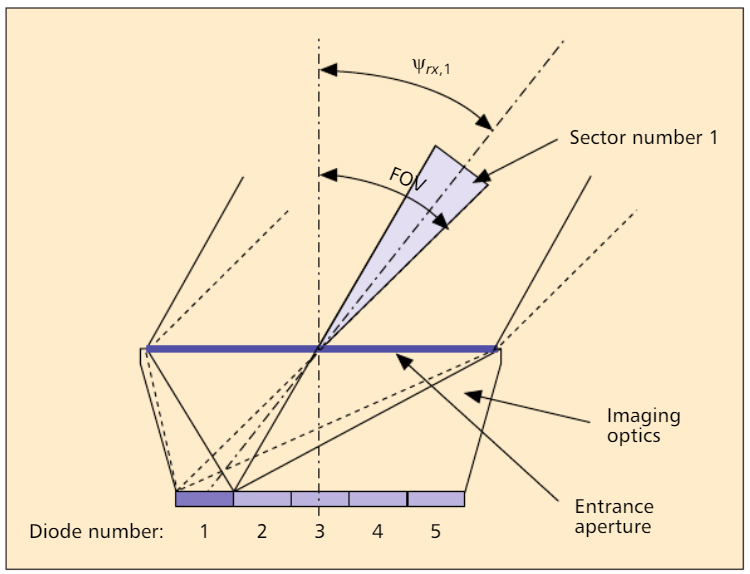
 a = [i for i in range(0,50,5)] a = np.array(a)*1e-3 #diameter of the receiver (in meters) a[0] = 1*1e-3 a_m = a*100 # for figures (in cm)

图2。 光电探测器的示意图：以第1扇区的示例为例，其入射角显示在第1光电二极管[2]上。

以及激光束（我们的发射器）的一些可能发散角：

 div_ang = [0.2*1e-3, 0.5*1e-3, 2*1e-3, 5*1e-3, 7*1e-3] div_ang = np.array(div_ang) #half of divergence angle

图 3.激光束发散角的图示。

接收机输入端的功率 （接收功率）可以通过公式[2]计算：

$P_ {rx} = \ frac {A_ {rx}} {2 \ pi R ^ 2} \左（1-\ frac {ln2} {ln（cos \ theta_ {div}）} \右）P_ {tx} \四倍[W]$

在哪里 $A_ {rx} = \ frac {d_ {rx} ^ 2 \ pi} {4}$ 是接待区， $d_ {rx}$ -接收镜的直径， $[R$ -卫星之间的距离， $\ theta_ {div}$ 是发散角的一半，并且 $P_ {tx}$ -发射功率。

 Prx_opt_dBm = np.zeros((len(div_ang), len(a))) Prx_opt = np.zeros((len(div_ang), len(a))) Pathloss_dBm = np.zeros((len(div_ang), len(a))) Pathloss = np.zeros((len(div_ang), len(a))) Arx_m2 = (np.pi/4)*(a**2) for f, dvangl in enumerate(div_ang): #received power Prx_opt[f,:] = (Ptx_opt*Arx_m2)/ (2*np.pi*(R**2))\ *(1-(np.log(2)/np.log(np.cos(dvangl)))) Prx_opt_dBm[f,:] = 10*np.log10(Prx_opt[f,:]*1e3) #path loss Pathloss[f,:] = (Arx_m2)/(2*np.pi*(R**2))\ *(1-(np.log(2)/np.log(np.cos(dvangl)))) Pathloss_dBm[f,:] = 10*np.log10(Pathloss[f,:]*1000)

好的，已经有东西了。但是这些物理上可以实现多少呢？

灵敏度限制

量子极限

回忆光子能量公式：

$E = hf \ quad \左[m ^ 2 kg / s ^ 2 \右]$

在哪里 $^ h$ = 6.62607004e-34 $m ^ 2千克/秒$ 是普朗克的常数，并且 $˚F$ -载波频率（Hz）。

在此之后，我们会进行一些小的启发。如果有人知道理论上的正当性或反驳-请分享！

所需能量（接收方每比特信息的最低能量至少可检测到某物）：

$E_ {req，Q} = N_ {ph} hf \ quad \ left [m ^ 2 kg / s ^ 2 \ right]$

在哪里 $N_ {ph}$ -检测1位信息所需的平均光子数。

光脉冲的理论能量：

 E_theor = 10*h*freq_opt

光脉冲（ APD二极管）的更现实的能量值：

 E_real_APD = 1000*h*freq_opt

光脉冲（ PIN二极管）的更现实的能量值：

 E_real_PIN = 10000*h*freq_opt

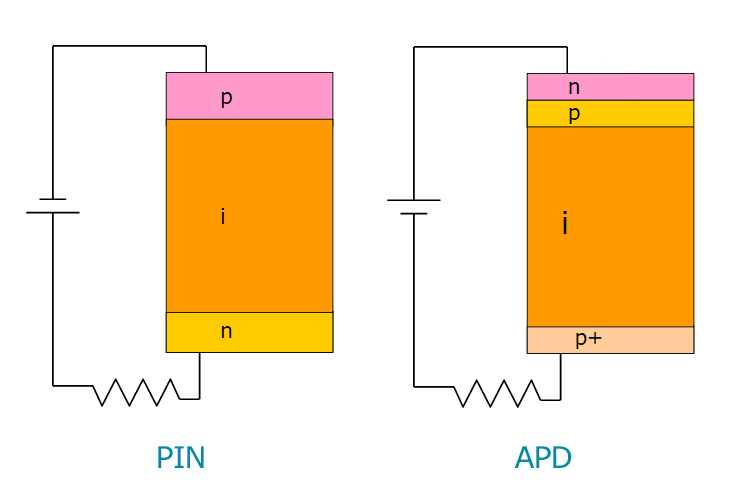
图4。 正在考虑的光电二极管的电路。

所需（最小）接收功率（最大灵敏度）：

$P_ {req，Q} = 10 \ log_ {10} \左（\ frac {E_ {req，Q} B} {10 ^ {-3}} \ right）= 10 \ log_ {10} \左（\ frac {E_ {req，Q} R_b} {10 ^ {-3}} \右）\ Quad [dBm]$

在哪里 $乙$ 是通信通道的带宽，并且 $R_b$ 是比特率。

 P_req_theor = 10*np.log10(E_theor*Bit_rate*1000) P_req_real_APD = 10*np.log10(E_real_APD*Bit_rate*1000) P_req_real_PIN = 10*np.log10(E_real_PIN*Bit_rate*1000)

但这还不是全部：调制也做出了有限的贡献。

错误概率限制

首先，我们将考虑调制OOK （开关键控）。

图5。 OOK调制原理的图示。

发生错误的概率（ BER ）为[2]：

$P_b = \ frac {1} {2} ercf \左（\ sqrt {\ frac {SNR} {2}} \右）= \ frac {1} {2} ercf \ left（\ sqrt {\ frac {P_ { req} ^ 2 \ gamma ^ 2} {2 \ sigma ^ 2}} \对）$

在哪里 $信噪比$ 是信噪比， $\ sigma ^ 2$ 是噪声方差（即噪声功率），并且 $\伽玛$ 是光电二极管的灵敏度（ photodioderesponsivity ）。

OOK的BER（PIN二极管）：

$P_ {b，PIN} = \ frac {1} {2} ercf \ left（\ frac {\ gamma P_ {req，PIN}} {\ sqrt {2 \ sigma_ {PIN} ^ 2}} \ right）$

因此：

$P_ {req，PIN} = \ frac {erfcinv（2P_b）\ sqrt {2 \ sigma_ {PIN} ^ 2}} {\ gamma} \ quad [W]$

OOK的BER（APD二极管）：

$P_ {b，APD} = \ frac {1} {2} ercf \ left（\ frac {\ gamma M P_ {req，APD}} {\ sqrt {2 \ sigma_ {APD} ^ 2}} \ right）$

因此：

$P_ {req，APD} = \ frac {erfcinv（2P_b）\ sqrt {2 \ sigma_ {APD} ^ 2}} {\ gamma M} \ quad [W]$

在哪里 $中号$ -这是一些参考增益。

噪音功率

您可能已经猜到了，噪声的计算方式也会有所不同。

PIN二极管的噪声功率

可以通过公式[3，p 11]计算热噪声：

$\ sigma_ {PIN} ^ 2 = \左（\ frac {4kT} {R_f} + 2qI_ {BE} \右）I_2R_b = N_0 + 2qI_ {BE} I_2R_b \ quad [W]$

在哪里 $T = 290千$ ， $k = 1.38064852e-23$ -玻尔兹曼常数 $R_f = \ frac {100} {2 \ pi C_d R_b}$ -直接抵抗 $C_d$ -光电二极管的容量， $q$ 是电子的电荷， $I_ {BE} = \ frac {I_C} {\ beta}$ -基极-发射极电流（ 基极-发射极或泄漏或偏置电流 ）， $I_2$ -针对热噪声的Personick积分的值（-我放弃了，我没有找到足够的转换，请告诉我）， $R_b$ -比特率 $N_0$ -噪声的频谱密度。

 Cd = 2*1e-12 #capacitance of the photodiode T = 290 #absolute temperature Rf = 100/(Cd*2*np.pi*Bit_rate) #photodiode resistance k = 1.38064852*1e-23 #Bolzman constant I2 = 0.562 #depends on filter (Personick integral) for match filter q = 1.60217662*1e-19 #electron charge Ibe = (0.25*1e-3)/200 #RESULT thermal_Noise_variance_add = 2*q*Ibe*I2*Bit_rate N_0 = 4*k*T/Rf #thermal noise density for PIN thermal_Noise_variance = N_0*Bit_rate*I2

APD二极管的噪声功率

为这个二极管做好准备-许多拉丁字母：

$\ sigma_ {APD} ^ 2 = \ frac {4kT} {R_f} I_2R_b + 2qI_dM_ {Si} ^ 2F_ {Si} I_2R_b = N_0 + 2qI_2R_b（I_ {BE} + M_ {Si} ^ 2F_ {Si} I_d）\大约N_0 + 2qI_2I_dR_bM_ {Si} ^ 2F_ {Si} \ quad [W]$

在哪里 $I_d$ -暗电流（暗电流）， $M_ {Si}$ 是典型的增益（硅）， $F_ {Si}$ -多余的噪声系数。

从以下参数中收集参数：

在本文中，未考虑输入场效应晶体管的噪声（输入FET噪声）和输入场效应晶体管的负载的噪声（输入FET负载的噪声）。在[3，p 15]中阅读有关这些术语的更多信息。

 Id = 0.05*10e-9 #dark current (500e-12) M_Si = 100 #typical gain F_Si = 7.9 #excess noise factor apd_noise_Si = 2*q*Id*I2*Bit_rate*(M_Si**2)*F_Si #noise

造型

收到功率

我们用公式中阐明的所有内容代替：

 r = 0.53 #A/W photodiode responsivity Pb = 10e-9 #Bit error rate (BER) P_req_pin = 10*np.log10((special.erfcinv(2*Pb)* np.sqrt(2*(thermal_Noise_variance+thermal_Noise_variance_add))/(r))*1e3) #in dBm P_req_apd_lin = special.erfcinv(2*Pb)*np.sqrt(2*(thermal_Noise_variance+apd_noise_Si))/(r*M_Si) P_req_apd = 10*np.log10(P_req_apd_lin*1e3) #in dBm fig = plt.figure(figsize=(10, 7), dpi=300) req_theor = np.ones((len(a_m),))*P_req_theor req_real_APD = np.ones((len(a_m),))*P_req_real_APD req_real_PIN = np.ones((len(a_m),))*P_req_real_PIN PIN = np.ones((len(a_m),))*P_req_pin APD = np.ones((len(a_m),))*P_req_apd a_m = a_m.reshape((10,)) plot(a_m, Prx_opt_dBm[0,:],'-o', label = '0.2 mrad') plot(a_m, Prx_opt_dBm[1,:],'-o', label = '0.5 mrad') plot(a_m, Prx_opt_dBm[2,:],'-o', label = '2 mrad') plot(a_m, Prx_opt_dBm[3,:],'-o', label = '5 mrad') plot(a_m, Prx_opt_dBm[4,:],'-o', label = '7 mrad') plot(a_m, req_theor,'k--', label = 'Sensitivity limit (theory)') plot(a_m, req_real_APD, '--*', label = 'Sensitivity limit (APD)') plot(a_m, req_real_PIN, '--', label = 'Sensitivity limit (PIN)') plot(a_m, APD, '-*',label = '1e-9 OOK BER limit (APD)') plot(a_m, PIN, label = '1e-9 OOK BER limit (PIN)') plt.gca().invert_yaxis() xlabel('Rx diameter (cm)'); ylabel('Prx and Preq (dBm)') legend() grid() plt.show()

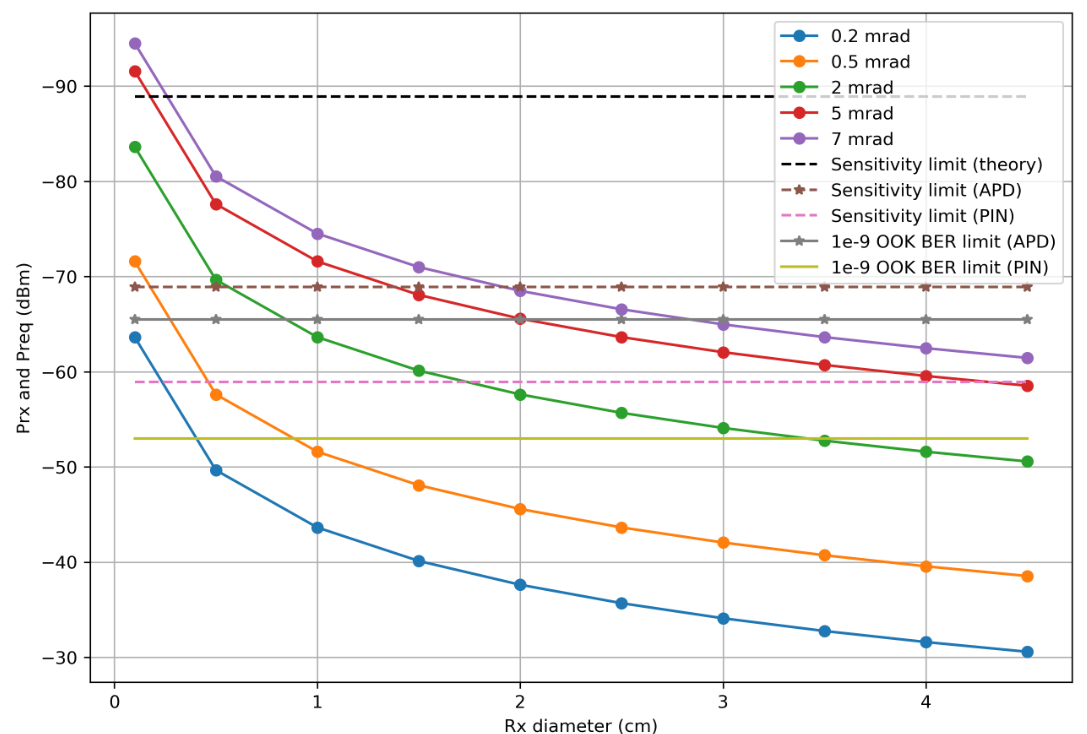
让我们解释一下：您需要查看曲线的相应水平线下方的那些部分。

发射功率

现在让我们看一下相反的问题：我们在接收侧固定一些电源，然后看看需要在发送侧施加哪种电源：

$P_ {tx，dBm} = P_ {rx，dBm} + | L | + | L_ {添加} |$

在哪里 $L = 10 \ log_ {10} \左[\ frac {A_ {rx}} {2 \ pi R ^ 2} \左（1-\ frac {ln2} {ln（cos \ theta_ {div}）} \右）\对]$ 是路径衰减，并且 $L_ {添加}$ -这是一些亏损的保证金。

 Prx_req_dB_APD = -65.5 Prx_req_dB_PIN = -52.9 margin = 5 Arx_m2 = np.zeros((len(a))) Ptx_variable_APD = np.zeros((len(div_ang), len(a))) Ptx_variable_PIN = np.zeros((len(div_ang), len(a))) #area rx Arx_m2 = (np.pi/4)*(a**2) for f, dvangl in enumerate(div_ang): #Ptx required Ptx_variable_APD[f,:] = Prx_req_dB_APD + np.abs(Pathloss_dBm[f,:]) + margin; Ptx_variable_PIN[f,:] = Prx_req_dB_PIN + np.abs(Pathloss_dBm[f,:]) + margin; fig = plt.figure(figsize=(10, 7), dpi=300) plot(a_m, Ptx_variable_APD[0,:],'-o', label = 'APD, 0.2 mrad') plot(a_m, Ptx_variable_PIN[0,:],'-*', label = 'PIN, 0.2 mrad') plot(a_m, Ptx_variable_APD[1,:],'-o', label = 'APD, 0.5 mrad') plot(a_m, Ptx_variable_PIN[1,:],'-*', label = 'PIN, 0.5 mrad') plot(a_m, Ptx_variable_APD[2,:],'-o', label = 'APD, 2 mrad') plot(a_m, Ptx_variable_PIN[2,:],'-*', label = 'PIN, 2 mrad') xlabel('Rx diameter (cm)'); ylabel('P_tx (dBm)') legend() grid() plt.show()

在我们的期刊文章中可以找到与电磁星际通道情况的比较。它还描述了最终我们拒绝这种情况的原因，但在此我将详细说明。

陷阱

在这里，我们受到参考书和数学公式的打击，但是仍然受到所获得结果的启发（是的，实际上是美丽的图形！），我们正在防御之前进行最后的会面。我们面临着新一轮的重要细节...

净重 第2名 ：恩，恩，很明显，有赢家。他们确信已经有了某种硬件基础。定位如何？您可能已经听说过PAT系统 （点印，征服和T货架）。

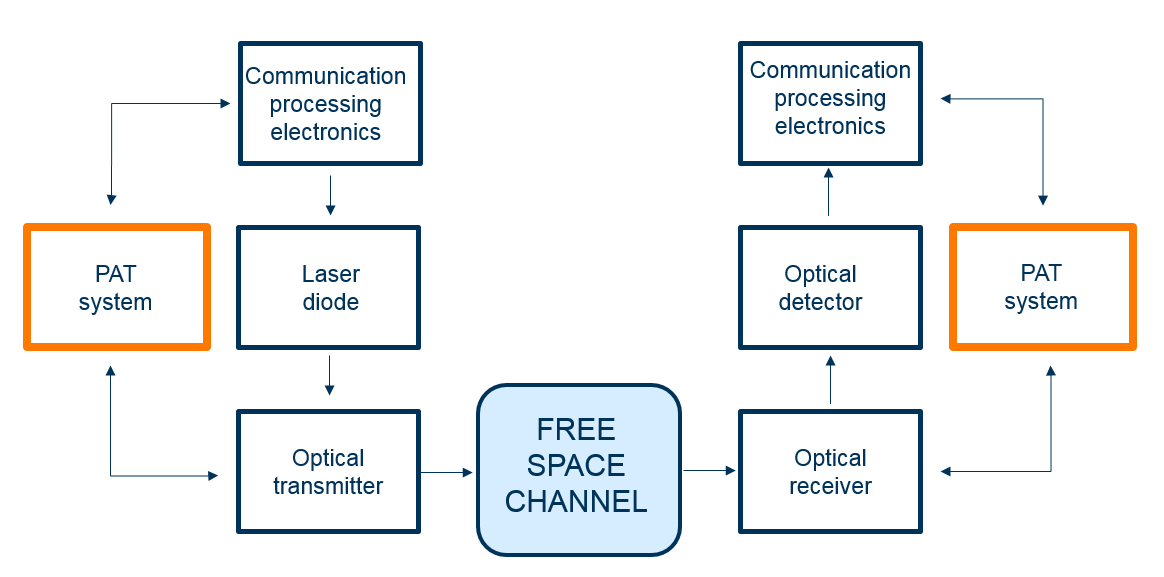
图 6.无线光收发器系统的简化图。

净重 No. 2 ：是的，有一些用于大型卫星的光信道的例子[4] ，但是，在这种情况下，您可以提供更大的接收器直径，更大的激光发散角和更高的发射功率。而且，我认为CubeSat本身在移动时会振动很大。但是，对于频率相对较低的无线电信道，这可能不是必需的，对于光学设备-您自己也可以理解。目前是否有如此精确的稳定和PAT系统？

我们非常体贴...

净重 2 ：就我而言，这就是我给您的积极评价。但是，我对您的建议是：从天堂降落到人间...

我们精疲力竭地失败了：我们决定不继续使用卫星光学系统进行该项目。而且，即使在我们的频繁会议中，我们也积累了一些倦怠...

但是，不，不，甚至学生希望的音符都会落入心中，即老师的怀疑态度是错误的。不，不，我想在现代技术成就中找到真正的概念。然后凝视向上...

文学作品

威尔逊（Welle）RP 的詹森（Janson），美国国家航空航天局（NASA）的光通信和传感器演示计划： // //第28届年度AIAA / USU小卫星会议。 -2014年。-S. 4-7。
沃尔夫（Wolf，M.）和克雷斯（Kreß，D.）（2003）短距离无线红外传输：与RF相比，链路buoget更为明显。 IEEE无线通信，10（2），8-14。
https://www.nii.ac.jp/qis/first-quantum/forStudents/lecture/pdf/noise/chapter12.pdf
Smutny B.等。 5.6 Gbps卫星间光通信链路 //自由空间激光通信技术XXI。 -国际光学和光子学会，2009年。-T.7199。-S. 719906。

但是我们不向光通信挥手吗？ 激光，太空，CubeSat