亲爱的读者您好！ 我向您介绍克里斯·赫克（ Chris Hecker）撰写的文章《物理学，下一个前沿》的英语翻译。

我是Java的新手开发人员，因此面临这样一个事实，即用于创建物理游戏引擎的材料仅以英语提供，因此本文进行了翻译。 该系列中还将有三篇文章，我会尽快发布。 祝您阅读愉快！

物理学的新领域

毫无疑问，每年游戏中的图形都变得越来越逼真。 如今，每个人都已经使用纹理贴图创建（或至少显示了屏幕截图）3D世界，并且当有足够的勤奋人员聚集在一起从事一个项目时，每个开发人员每秒都可以绘制数十亿个逼真的多边形和阴影多边形。 用技术术语来说，要想创造高水平的游戏还需要做些什么？ 每位拥有“在21天之内学会使用3D硬件”一本书的开发人员，都能创造出真正令人印象深刻的游戏吗？

一点也不。 高端开发人员将继续提高许多不同技术（例如GUI复杂性，人工智能和网络）的标准。 当然，所有这些都是非常重要的，如果不指定详细信息，我们甚至无法认真讨论其中的任何一个。 不过，有一种技术适用于所有事物，我认为，在不久的将来它将成为决定性因素：物理学。

请考虑以下示例：您是否还记得Duke Nukem 3D早期级别之一中的这些巨大的旋转齿轮？



图1.游戏“ Duke Nukem 3D”的屏幕截图

试想一下，它们的旋转不是由循环动画来描述，而是由真实的物理引擎来描述。 就像在印第安纳·琼斯的电影中一样，其中的一个齿轮偏离了给定的角度，并在您身后的走廊上滚来滚去，齿轮突然变得不仅仅是游戏装饰。 或想象一下，从火箭发射器发射齿轮后，它会滚落走廊并压死您的朋友，后者已经悄悄地追杀了您！ 物理引擎使这种情况成为现实。

物理模拟是整个游戏世界的源泉：由于它，如果您理解我的意思，“这里”就位于这里。 如果玩家将渗透到另一位玩家，关卡或关卡的墙壁中，或者如果没有感觉到质量和质量矩，那么世界上任何图形上的魔术都将不允许玩家投入游戏过程。 迪士尼的动画师发现，群众的这种感觉是将好动画与坏动画区分开的原因。 根据弗兰克·托马斯（Frank Thomas）和奥利·约翰斯顿（Ollie Johnston）的史诗《迪斯尼动画：生命的错觉》，迪斯尼动画师，甚至只是在工作室里挂一张海报，都应该问自己：“他们的绘画中是否有很大的重量，深度和平衡性？” ？

但是今天几乎每个游戏都有一个物理引擎，对吗？ 毫无疑问，这就是阻止您的车掉落在游戏世界边缘的原因，这要归功于您的角色在跳跃时不会飞入太空，并且当火箭在附近爆炸时，这会使您的船只驶向侧面。 但是，现代游戏中的大多数物理引擎都非常薄弱。 他们仅能应付阻止赛车掉落在世界边缘的任务，但他们的能力不足以将游戏提升到一个新的高度-撞毁的汽车残骸可能会在赛道上爆炸，造成一堵墙和其他汽车翻滚。

其他经常被忽略的物理效果包括：从切线罢工产生的简单扭曲效果，到游戏中的角色自身保持平衡和移动，与静态动画不同。 我相信许多开发人员会忽略这些可能性，因为他们不了解描述物理的数学方法，或者太忙创建纹理贴图来学习它。 使用3D的硬件冲击将解决后者，我将开始撰写新的系列文章。 第一篇文章将涉及手续。 在周期结束时，您可以自己创建一个物理引擎，借助令人难以置信的逼真度或有趣但持久的超现实主义，使玩家完全沉浸在游戏中。

警告！ 物理=数学，为了完成一个有趣的项目，您将不得不同时使用两者。 在让您惊慌失措之前，让我注意一下描述物理的数学不仅优雅而美丽，而且还具有实用性。 也就是说，它不是数学的抽象数学。 我们使用的每个方程都有实际的物理意义。 我们根据物理模型创建方程式，然后这些方程式告诉我们模型如何及时运行。

大企业

物理学是一个广泛的科学领域。 但是，我们对它称为“动力学”，或更确切地说是“固体动力学”的一小部分确实感兴趣。 动力学可以根据相关部分来定义-运动学（时间运动学说）。 运动学并不关注导致运动的原因，也不关注身体如何在原处结束，它只是描述运动。 相反，动力学描述的是影响运动学值随时间变化的力和质量。 如果飞行时间为10秒且初始速度为50公里/小时，并且棒球的轨迹是一条直线，那么棒球将飞多远，这是一个运动学问题。 如果我用蝙蝠将棒球击中，那么棒球球将在地球的重力场中飞行多远-这是一个动态问题。

描述实体的动力学部分与我们为模拟对象添加的约束有关。 实体的形状在仿真过程中不会改变-实体比果冻状的更可能是木制或金属的。 例如，我们可以通过从实体构造人体的各个部分并在它们之间创建韧带来创建一个人的关节连接体，但是我们不会指望在压力或类似作用下弯曲的骨头。 这将使我们能够简化方程式，而不会损失物体有趣的动态行为的质量。

即使我们只考虑动力学的一小部分，但刚体的动力学仍需要一系列文章来解释其本质。 我们通过研究计算机编程的基础知识来开始我们的旅程，以描述在力作用下平面刚体的运动。 我坚持不懈地重复“计算机编程”，因为除了我们为运动学和动力学编写的方程式之外，我们还将学习如何使用带有浮点数的计算来求解这些方程式，这对于每个程序员都至关重要。 我之所以说“扁平固体”，是因为我们将仅在下一篇文章及以后的文章中处理二维世界。 原理（实际上不仅仅是方程式）也可以传递到三维世界，但是绝对肯定，二维世界中的一切都简单得多，因此我们将在那里进行研究，直到我们对进入三维空间充满信心为止。 在以后的文章中，我们将学习描述旋转的效果，物体接触的过程，当然还有如何在三维世界中实现所有这些功能。 好吧，足够的话！ 让我们开始吧！

使用导数

这可能会让您感到意外，但实际上您不能仅通过推动它来移动对象。 我知道，您认为通过将这本杂志扔进垃圾箱来写这样的废话而证明与我相反，这是错误的，但这是真的！ 仅对弹匣施加压力绝不会直接影响弹匣在太空中的位置。 实际上，压力甚至不会直接影响其速度。 压力实际上影响的是期刊的发展，实际上，这是科学史上最重要的结论之一。

为了利用这个事实来做一些有趣的事情，我们首先需要讨论身体位置与速度和加速度之间的关系。 实际上，所有这些值都是非常紧密相关的（您可能知道）：速度是随时间变化的身体坐标的指标，而加速度是速度变化的指标。 研究这些量随时间变化的主要工具是微积分。 如果您了解这一点，那么我们继续。 我想你数学很好。 我们将仅使用简单的标量和向量计算（导数和积分），但是如果您对整个数学都非常熟悉，那将不是多余的。 供参考：我最喜欢的关于计算的书是Thomas和Finney撰写的《具有解析几何的微积分》。

坐标，速度和加速度是运动学，本文将对此进行讨论。 固体在二维世界中的位置显然是一对坐标X和Y，它们表示身体某个给定点的空间坐标。 坐标向量的导数是速度向量，它向我们显示该点朝哪个方向移动（如果忽略旋转，则该物体为主体，而现在正在发生旋转）以及该点移动的速度。 向量演算只是向量每个元素的标量演算，因此X坐标的导数是相对于X的体速度，依此类推。 我们介绍以下符号。 设物体的坐标为矢量r，速度为矢量v或带质数的矢量r。 我们得到等式：

$$

$${{dx} \ over {dt}} = v = r'$$

等式1

如果我们将速度矢量相对于时间进行区分，这将显示坐标矢量如何随时间变化。 加速是通过类比确定的。 这是速度的一阶导数或坐标矢量的二阶导数：

$$

$${{d ^ 2 r} \ over {dt ^ 2}} = r''= {{dr'} \ over {dt}} = {{dv} \ over {dt}} = v'= a$$

方程式2

加速度的积分将为我们提供速度，而积分两次的加速度将获得坐标。

运动学中的这些关系表明，我们可以找到对象的加速度，可以随时间对其进行积分以获得速度和坐标。 正如我们将在后面看到的，我们将在仿真代码中多次进行积分，并为每一帧计算实体的新位置。 万岁动画！

这是我们可以分析集成的一维世界的简单示例。 让我们同意，我们想要找到从最后一帧的末尾到当前帧的时间的坐标变化以绘制当前位置。 接下来，我们说固体的加速度等于5个任意单位/秒^ 2。 我们将从最后一帧结束起经过的时间用作变量t（在积分元素dt中）。

$$

$$v（t）=∫adt=∫5dt= 5t + C$$

方程式3

上面的等式表明速度是从最后一帧开始经过的时间的函数。 我们发现积分常数C等于积分周期开始时的初始速度（在t = 0时）。

$$

$$v（0）= 5（0）+ C$$

$$

$$v_0 = {C}$$

方程式4

$$

$$v（t）= 5t + v_0 {}$$

现在，我们对速度方程进行积分以找到坐标（再次，不要忘记积分常数）：

$$

$$r（t）=∫v（t）dt =∫5t+ v_0 dt = {{5} \ over {2}} t ^ 2 + v_0 t + r_0$$

方程式5

基于方程式5，如果我们知道初始坐标和速度（将从最后一帧开始获取）和经过的时间，则只能以给定的加速度找到当前位置。 输入变量是时间，函数的值是当前位置。 我们还将在公式4中指出时间，以便计算最终速度，以便我们可以将其用作下一帧的初始条件。

愿力量与你同在

现在，我们意识到需要正确设置加速度以集成运动学方程，以便获得动画。 舞台上扬声器的输出。 还记得我说过的，通过按压某些东西，您仅直接影响身体的加速度吗？ 好吧，“施加压力”只是短语“施加力”（动力学中两个关键变量之一）的委婉说法，现在我们可以求助于牛顿，以了解力如何影响加速度。 牛顿第二定律将力F与质量的导数（动力学的第二量级）乘以速度。 质量与速度的乘积称为“身体动量”，用p表示：

$$

$$F = p'= {{dp} \ over {dt}} = {{d（mv）} \ over {dt}} = mv'= ma$$

方程式6

质量是我们现在正在使用的速度的常数，它来自方程式6的导数，并且我们得到了众所周知的方程F = ma（尽管我确定牛顿最初是通过动量的导数来确定力的）。

如果仅处理实质性问题，则方程6是动力学中需要的。 对于给定材料点的给定力，可以通过将力除以质量来获得加速度。 这为我们提供了加速度，将有助于解决上述示例中的运动方程。 但是，我们正在处理的是质量分布在某个区域（体积，涉及到三维世界）的实体，因此我们仍然需要工作。

首先，将实体视为一组点质量。 我们将固体的总动量pT定义为组成身体的所有点的动量的总和（我使用上标度，因为我想更清楚地显示哪些数值属于这些点）：

$$

$$p ^ T = \ sum_ {i} {m ^ i v ^ i}$$

式7

通过引入质心（CM）的概念，我们可以大大简化对刚体动力学的分析。 指向质心的矢量是从实体的所有质量点指向的矢量的线性总和，除以整个实体的质量M：

$$

$$r ^ {CM} = {\ sum_ {i} {m ^ i r ^ i} \超过{M}}$$

方程式8

使用质心的定义，我们可以通过将等式8的两边乘以M，对其求微分，然后将结果代入等式7来简化等式7：

$$

$${{d（Mr ^ {CM}）} \ over {dt}} = {\ sum_ {i} {} {{d（m ^ ir ^ i）\ over dt}}} = {\ sum_ {i} {} {m ^ iv ^ i}} = p ^ T$$

式9

等式9的右侧是等式7中定义的总动量。现在让我们看一下等式的左侧：这是质心的速度乘以整个身体的质量。 将右侧移到左侧并获得：

$$

$$p ^ T = {{d（Mr ^ {CM}）} \ over {dt}} = Mv ^ {CM}$$

式10

从等式10可以得出，线性动量等于总质量乘以从质心指向的速度，因此如果我们知道物体的质量和质心的速度矢量的方向，则无需对等式7求和即可找到动量。 此外，计算的所有最终结果都是找到整个身体的积分，但质心存在并大大简化了根据式10的总动量的确定，因此我们不必担心-找到线性动量，我们可以将物体视为具有给定速度和质量的物质点。

以此类推，总力是总动量的导数，因此质心的概念可用于简化力方程：

$$

$$F ^ T = p ^ T = Mv'^ {CM} = Ma ^ {CM}$$

式11

简而言之，从等式11可以得出，我们可以考虑所有与实体相互作用的力，好像它们的和矢量对质心点（包含整个身体的质量）有影响。 我们将力（读取的重力）除以M，以找到质心的加速度，然后对加速度进行及时积分，以获得身体的速度和坐标。 因为 在下一篇文章之前，我们将忽略旋转的影响；我们已经拥有描述刚体动力学所需的所有方程式。 请注意，公式11不包含有关向身体施加力的方向的信息。 当我们处理线性动量和质心时，这会弹出，我们只需要向CM施加力即可找到质心的加速度。 在下一篇文章中，当我们在这些力的影响下计算身体的旋转时，我们将看到如何使用力的坐标。

欢乐颂

在此阶段，我们可以考虑分析积分的另一个示例，它使用公式11来查找质心的加速度，而不是任意选择的值=5。但是，由于分析积分通常没有适用的值，因此我们面临着一个严重的问题，因为它太复杂了，因此我们将集中于所谓的常微分方程（ODE）的数值积分。 哇，现在听起来像是真正的数学！ 一旦了解了这一点，就该提高标准了。 幸运的是，ODE的数值积分并不像乍看起来那样困难！ 为了理解这意味着什么，我们从言传身教！

因此，微分方程是一个方程，除了函数本身，独立变量和参数外，还包含因变量的导数。 这很冗长，但这是一维世界中随时间变化的力的一个示例：F = 2t，F是从属量，t是独立的。 F的值仅由F确定。让力方程式仅取决于我们身体的速度。空气阻力随着飞机速度的增加而增加。让我们回到一维世界的例子中，如果F = -v意味着摩擦力使速度减慢，速度会变慢？我们有一个问题，因为我们按如下公式求解方程：F = ma = -v，然后除以m得到（记住加速度是速度的导数）：

$$

$$a = {{dv}\over {dt}} = {-v\over m}$$

公式12

此微分方程（速度方程包含方程12中的速度导数）之所以称为常微分方程，是因为它仅包含因变量的常导数（与偏微分相反，偏微分构成了偏微分方程[PDE]，而我们不知道这些微分方程我们会谈）。

现在，让我们继续我们的短语的下一部分：集成。我们先前如何积分dv / dt来在等式的条件下找到v？

这似乎令人难以置信，但是物理学中几乎每个方程都是微分的，因此对ODE进行了充分的研究。微分方程通常可以在物理学中找到，因为定量数量的变化率通常取决于数量本身。例如，我们已经注意到，制动（速度变化的幅度），包括空气阻力的速度，取决于速度。物理学中的其他示例：冷却（热量损失的速度取决于当前温度）和放射性衰变（衰减速度取决于存在的放射性物质的数量）。

我们这句话中的最后一个词-数字-是我们的救赎。我之所以这样说是因为，即使是最简单的方程组，微分方程组的分析积分理论也是庞大而令人困惑的。尽管具有讽刺意味的是，使用计算机数值方法进行ODE的集成实际上相对容易理解。接下来，我将描述一个基于Euler方法的简单数值积分器，并将在下一篇文章中对其进行完善。

几乎所有的数值积分器，但没有像欧拉方法那样明确的数字积分器，仅基于通过斜率的一阶导数进行计算的旧定义：dy / dx根据x确定y的斜率。例如，如果我们有线性方程y = 5x，则dy / dx = 5意味着对于任何x，斜率都是一个等于5的常数，并且您可以假设，这是一条直线。一个更困难的例子是抛物线y = x2。在这种情况下，dy / dx = 2x，这是确定每个x坐标的新倾斜度的函数。我在图2中描绘了y = x2：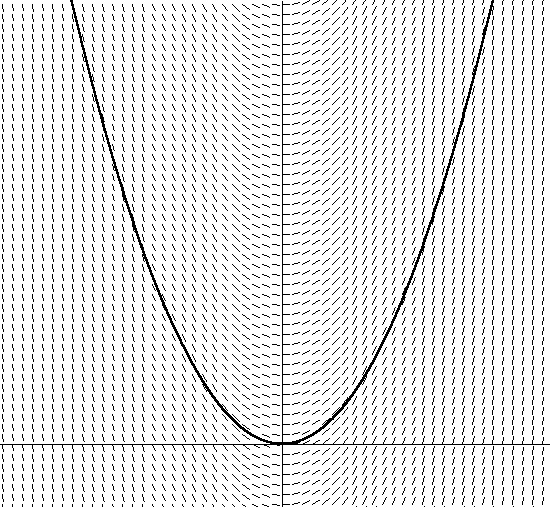



图 2。y = x2

除此之外，我还通过求解所有x的等式dy / dx = 2x + C来绘制矢量斜线的方向。请注意，在这一点上，倾斜矢量的角度等于切线角度的切线。还要注意，有许多不同的抛物线满足切线组的角度，只是沿y轴的位移不同。这些抛物线中的每一个都是通过使用不同的积分常数获得的，积分常数包含在方程dy / dx = 2x + C中。我所描绘的抛物线的积分常数为0。如果我选​​择另一个常数，例如1，则可以得出方程y = 2x +1。这意味着存在类似的抛物线，其沿y轴移动了1个单位。

现在考虑一下这样一个事实：如果您不知道图2中由抛物线定义的向量的域，则只需坐在一个水坑中即可。因此，如果要求解切线方程，则只需遵循矢量在每个点上的方向，并根据矢量场方向的变化来改变方向。一段时间后，您会惊讶地发现，根据开始的位置，您正在沿着抛物线轨迹（或沿着抛物线的一部分）移动。没有意识到这一点，您对向量场的方程进行了积分。您仅使用导数方程式（在向量字段中移动时计算dy / dx）找到了特定的抛物线形（取决于起始位置或初始条件）。

对一个实数微分方程做同样的事情也很简单。对于类型dy / dx = f（x，y）的微分方程，找到导数dy / dx作为与f（x，y）的切线，可以描述x，y图上每个坐标的切线的倾斜角度。如果要绘制由dy / dx = f（x，y）给定的向量场，则可以通过在每个点处找到导数并沿该方向跟随，以抛物线类推其后。图2显示了方程12（即空气阻力方程）的矢量场，其中沿垂直轴的速度和沿水平轴的时间（我在该图中任意选择m = 1）。



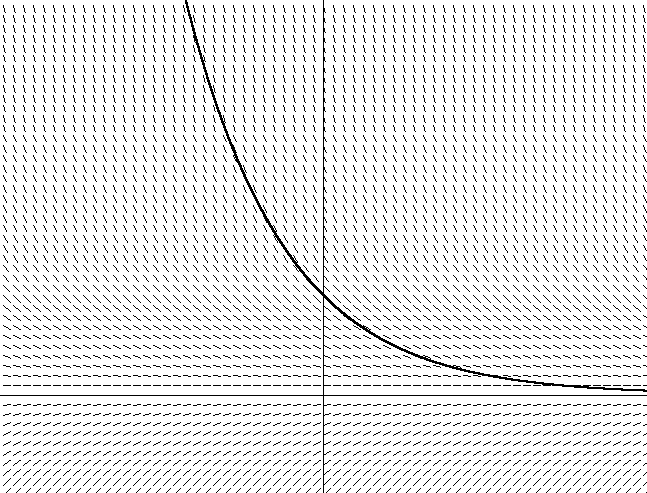图3. dv / dt = -v / m

它还显示了许多可能的曲线之一。您可能会注意到，如果选择图形中的起始位置（取决于方程式中的初始速度），则随着时间的流逝，速度将趋于零，因为摩擦力会降低身体的速度。您还可以看到速度降低如何取决于当前速度值-移动得越快，速度降低得越快。当从公式12得出相同结论时，这一点变得显而易见。

数值积分与我们在图表上所做的相似。用于数值积分的Euler算法通过找到方程的导数（在本例中为-v / m，带有摩擦力）来简单地遵循初始位置来确定矢量场，以确定当前点的斜率，然后根据需要随时间逐步向前移动沿斜率的h值不变。然后，在特定时间间隔后，将计算新位置以确定新斜率：

$$

$$y_{n+1} ≈ y_{ n } + {h(dy_{ n })\over dx}$$

或更确切地说，对于我们的空气阻力方程式：

$$

$$v_{ n+1 } ≈v_{ n }+{h( -v_{n})\over m}$$

显然，Euler方法在每个时间步长上都会产生很小的误差，这是因为实际速度矢量（以及解曲线）在每个点处都有偏差弯曲，并且Euler算法与倾斜角度略有偏离。但是，如果时间步长h很小，则误差趋于零。将来我们将对此进行更详细的讨论。

这就是使用Euler方法进行数值积分所需的所有知识。您可能会问我们如何整合速度以获得坐标。类似地，我们再次简单地使用Euler方法对dr / dt = v进行积分，就像我们对dv / dt = a进行积分一样。我们得到两个相连的微分方程（我们的又一个胜利）：

$$

$$v_{n+1} ≈ v_n+hv'=v_n+{h F_n\over M }$$

$$

$$r_{ n+1 } = r_n + hr_n'= r_n+hv_n$$

这为我们提供了一种替代算法，用于在任意施加力作用于对象上之后计算坐标（这可能取决于我们看到的速度或时间，甚至取决于我们身体和其他物体的位置，或者一次取决于所有物体！）。对于欧拉方法，所施加的力是什么样的并不重要，因为您可以随时计算它。欧拉对力对质量的影响程度（倾斜）很感兴趣，仅此而已。
我的空间不足，因此无法提供链接。下次，我将推荐各种精彩的书籍，我们将弄清楚如何计算固体的旋转。

尽管他的身体不像我们想要的那样坚固，但克里斯·赫克（Chris Hecker）却富有活力。如果您施加武力，他将回复电子邮件checker@bix.com。

译者的注释：这里有一个双关语，文章的主题及其内容都会显示出来。

PS翻译的作者特别感谢berez和MarazmDed的用户对翻译的编辑。谢谢你