在数十次动态测试（例如，研究车辆的振动活动时）中，“研究对象”被数十个传感器粘贴，可以轻松地为我们提供大量数据，但通常不清楚如何处理。 具有大量自由度的系统动态过程的仿真建模也是如此。
对于那些不经常遇到问题的人来说，这可能并不完全清楚，但是-通常，观察时间和空间上随机过程的相应动画几乎是没有意义的。 它破裂的地方或为什么会这样晃动-通常“不可见”。 除了动画，他们还提出了什么，下面我将告诉您，但我会推荐这一点。
通过基本过程，还可以获得振动本身的空间“形式”，而且，恰恰是给定载荷条件下的实际表现形式及其表现形式的强度（分散；如果需要，过程本身）。
图1将多通道响应分解为伪形式。 “粘稠介质中的细绳”（见图2）
除了动画之外，众所周知，“成对”研究（互谱等）当然不能给出总体图。
这种方法非常明显-通过“切出”对应于频谱图中共振峰的非常窄的光谱带，频谱图（再次“成对”）方法产生几乎形式的几乎谐波（高度相关）的振动。
除了明显的技术复杂性之外，此类方法的缺点还在于，您通常需要“成功”选择“参考”通道，但这并不总是可能的。 结果，在过程的相互阶段会发生很大的错误。 此外，由于线性系统的特性，独特的振荡空间形式且没有此类错误，可能会变得“复杂”（非相位），通常用于（但不总是）显着降低其用于后续主观分析的价值。
众所周知，对扭转振动的4通道研究（平均公共汽车的承载系统）是通过研究人员的灵感确定的空间振动形状在一个过程中分配的-添加了对角线位于身体各个角落的两个传感器的读数（取自“ +”），将它们减去（取自“-”）另外两个轴对称的证词。
即使只有少量的传感器，这种方法也不是完全好的。 例如，卡车的车架通常分别在副发动机（前）部分具有更大的延展性，并且具有扭转形状，也许应该以更复杂的形式进行假设（前传感器的系数可能会“增加”，同时还要证实接受的问题）。型号）。 有了大量的监视渠道，所有这一切都非常复杂且缺乏合理性。
以前由我（可能不仅是我）提出过一种由其他实验或模型确定的几种形式的振动（模态）的显式分离（分为单独的过程），后来被我的院长称为“模态分解方法”。 本来应该以这种方式分析现场测试的结果，并通过基准测试（或有限元建模）确定其自身形式的向量。
实际上，他们是这样做的，但同时事实证明了这一点。
显然，与“多边形”实验者相反，“基准实验者”可用于同步观察真正的干扰过程。 这给他们带来了很大的优势-他们可以确定真正的传递函数，并使用可用的硬件和软件通过实验确定其自身的结构振动形式和频率（基于couvfitting，“目视”“削减”频率范围，并向系统指示存在多少形式）找到；还有艺术而不是科学，但仍然如此）。
但是 他们显然避免了探索诸如汽车装配之类的物体，而更倾向于使用单个框架，支撑体等。 -阻尼非常低的物体。 它涉及模态台架试验-确定固有频率和形状。 与模拟无关。 可以通过实验从实验上获得在阻尼稍强的物体上的合理的固有振动模式，但难度要大得多。
事实证明，非常有价值的信息与这些“首选项”有关。 如果只是非常简短地总结，那么仅是随后逐渐得出的结论：尽管构想是“美丽的”，但努力不使构想准确地分解为真正正确的构造形式却几乎不值得。
如果它“在您的手指上”，那么原因很可能是这样的-根据外部干扰，“自然振动模式”（更确切地说，是与自然振动模式相对应的固定“模式”过程）很可能像这样或否则，它们相互关联，实际上形成了某种其他形式的空间振动，它们彼此之间有某种程度的差异，这自然表现为强烈依赖于结构的阻尼。
作为“相反”的简要解释-当然，两个不同的“未阻尼”谐波是不相关的。 （说明。在没有“显着的非线性”的情况下，以及在“复杂的形式”之外，在线性系统中具有“不成比例的”阻尼，都观察到了上述“混合自身形式”的影响。）
基于上述内容，建议将系统的响应表示为几个独立于相关过程的总和，例如某些形式的振动（弯曲，扭转等）。 这样的分析非常简单，通常它会给出非常有价值的结果。 所获得的形式可能与系统的振动本征模式相似，也可能不相似，但是它们始终在真实的外部影响条件下精确地反映系统的行为。 此外，它们反映的内容尽可能简单和有益，并且按其方差排序的序列是一个近似序列。
为了获得我们感兴趣的分解，我们考虑（1），
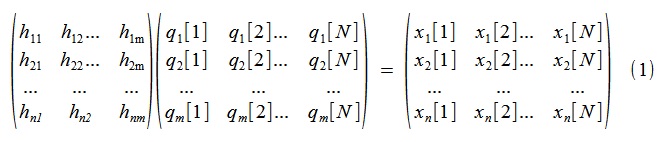
或者，同样，紧凑地（2），
其中
x是系统的n通道物理响应，其中N个样本的持续时间是在实验中直接获得的，
q是m通道具有相互不相关的通道的真实“模态”过程，H是描述所需的同相（“真实”）振动模态的列矩阵。
一般而言，随后会期望m <n（形式数小于物理响应通道数），但是最初我们假设m = n，则如果H和
q的秩为n，则（2）在任何情况下都满足且没有残差，我们显然得出
| H·Rqq [0]·H T = Rxx [0]（3） |
或更详细
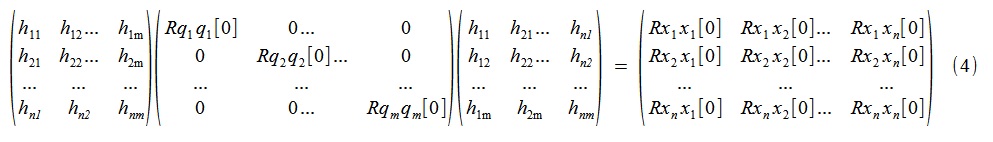
也就是说，寻找这种振动的“伪适当”模式以及相应的不相关（零滞后）过程
q的搜索减少到对称矩阵Rxx [0]（由过程
x的自相关和互相关的值组成）的频谱分解（就特征矢量和数量而言）滞后Δτ= 0）它自己的正交向量为我们提供了所需的形式，而实际特征值为我们提供了相应过程的方差（除了重要的过程外，方差约为0，因此实际上通常m <n）。 如果需要，您仍然可以以临时实现的形式自行构建流程，查找其频谱等。
为了阐明上述内容，我们考虑一个具有五个自由度的线性机械系统模型，大致模拟了弦在粘性介质中的行为（图2），
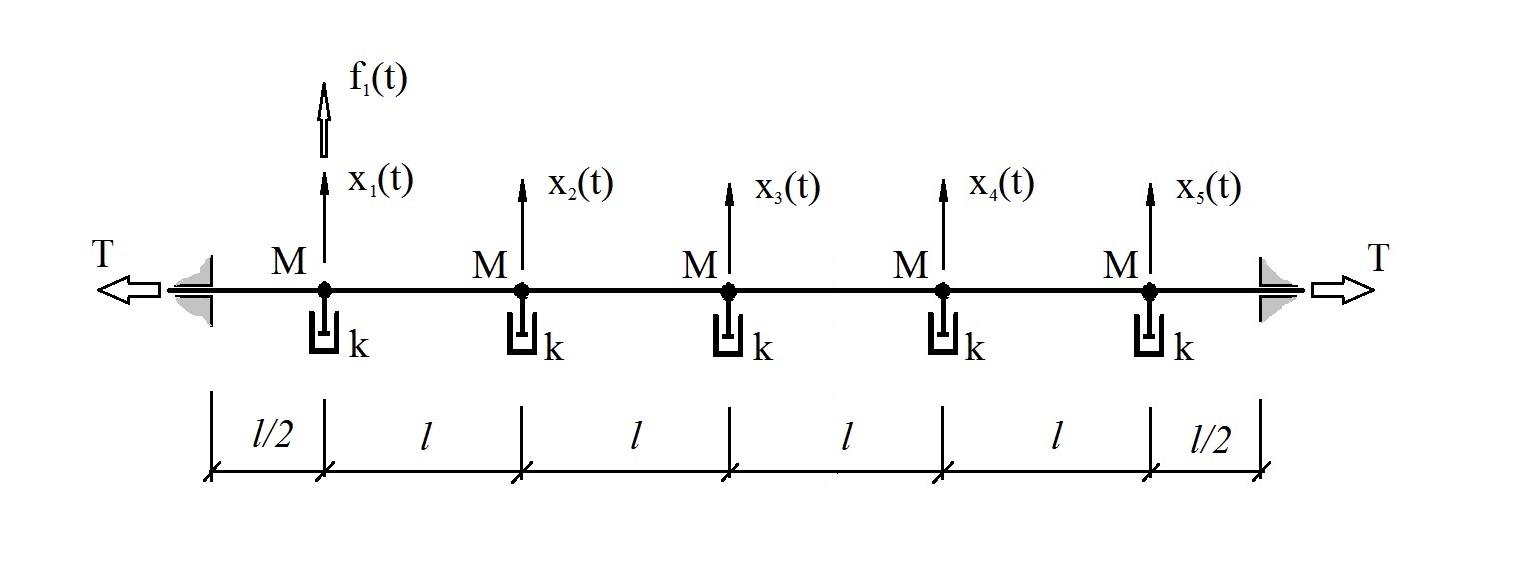图2测试系统在粉红噪声类型的随机扰动f
1 [i]（图3），采样间隔Δt= 0.01 s，执行长度25000个样本的影响下振荡（此后，通过Welch方法获得PSD估计值，段长度1024，应用Hamming窗，细分重叠60％。）
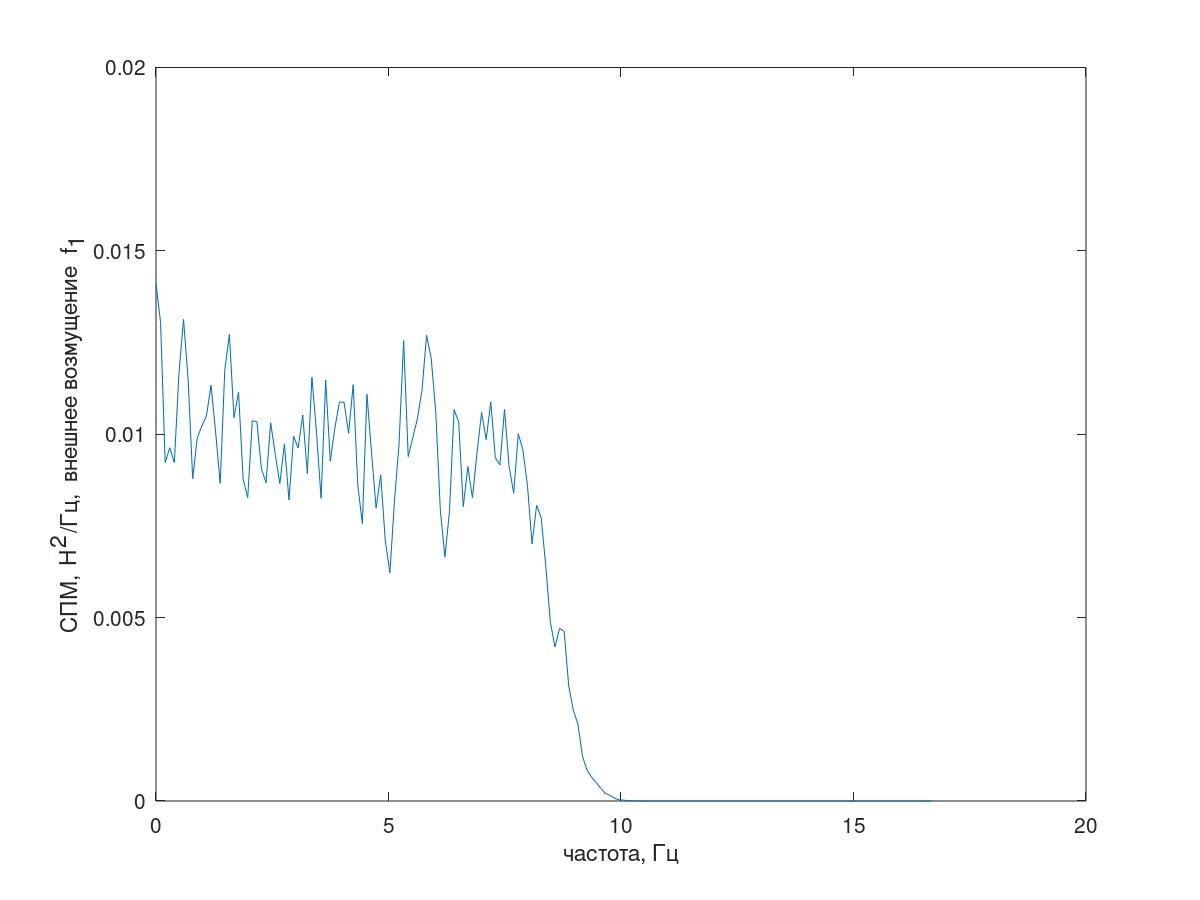图 3外部干扰频谱。
临时实施干扰的片段如图4所示。
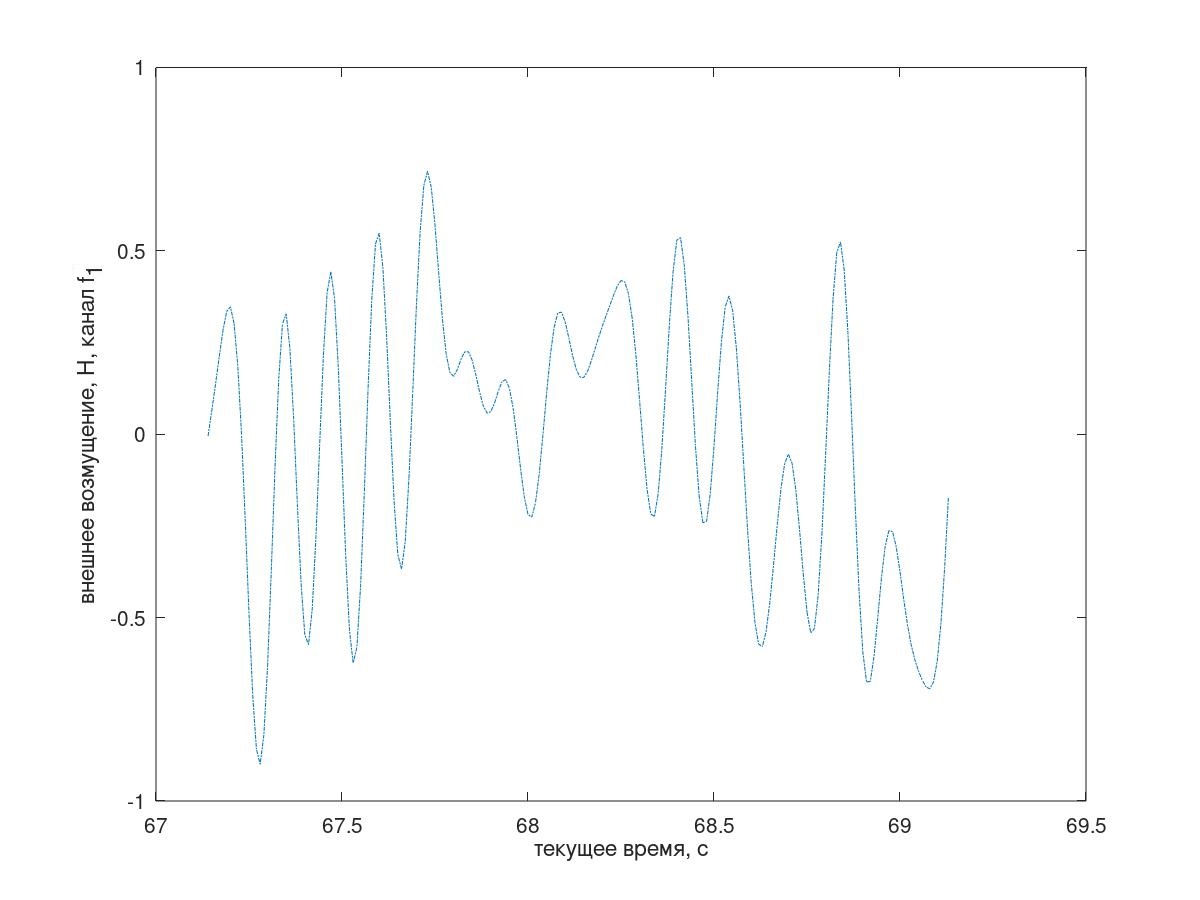
图4临时执行传入干扰的片段
在连续时间内，模型是扩散方程组（6），
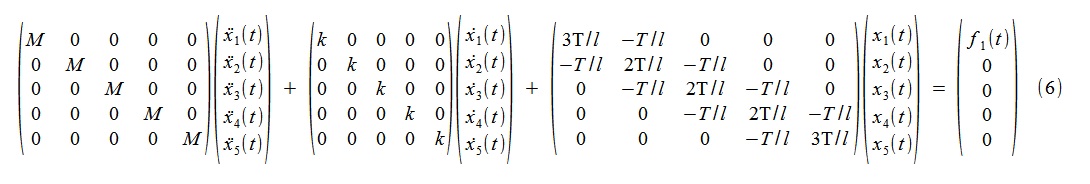
其中M = 1kg，k = 10kg / s，T = 2000N，l = 1m。
相应的（显而易见的）矩阵在数值上等于以下各项：
系统的频率响应之一如图5所示。
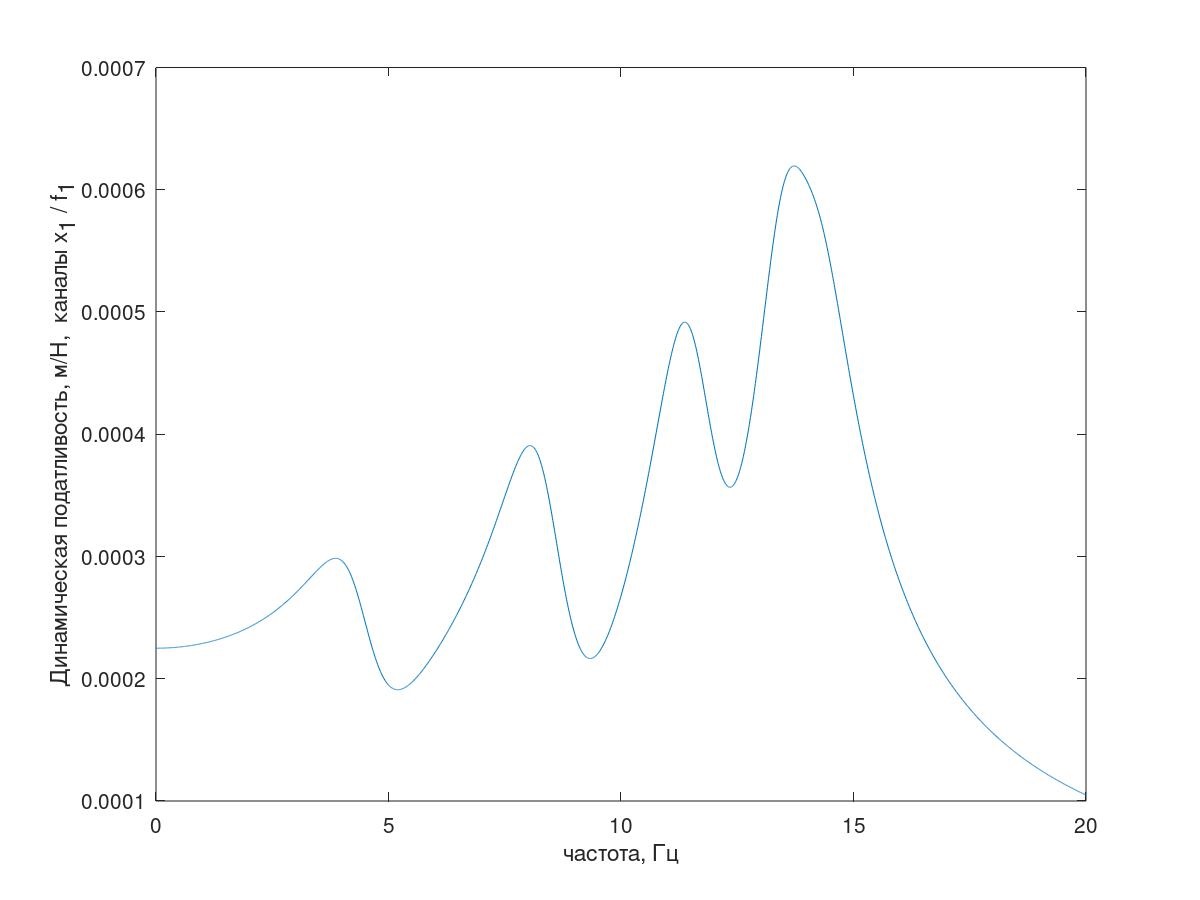图5。 测试系统的频率响应（说明-谐振峰的数量全部按顺序排列，如图5所示，这是对系统的频率响应进行了有条件减小的阻尼（k = 1 kg / s）的解释）
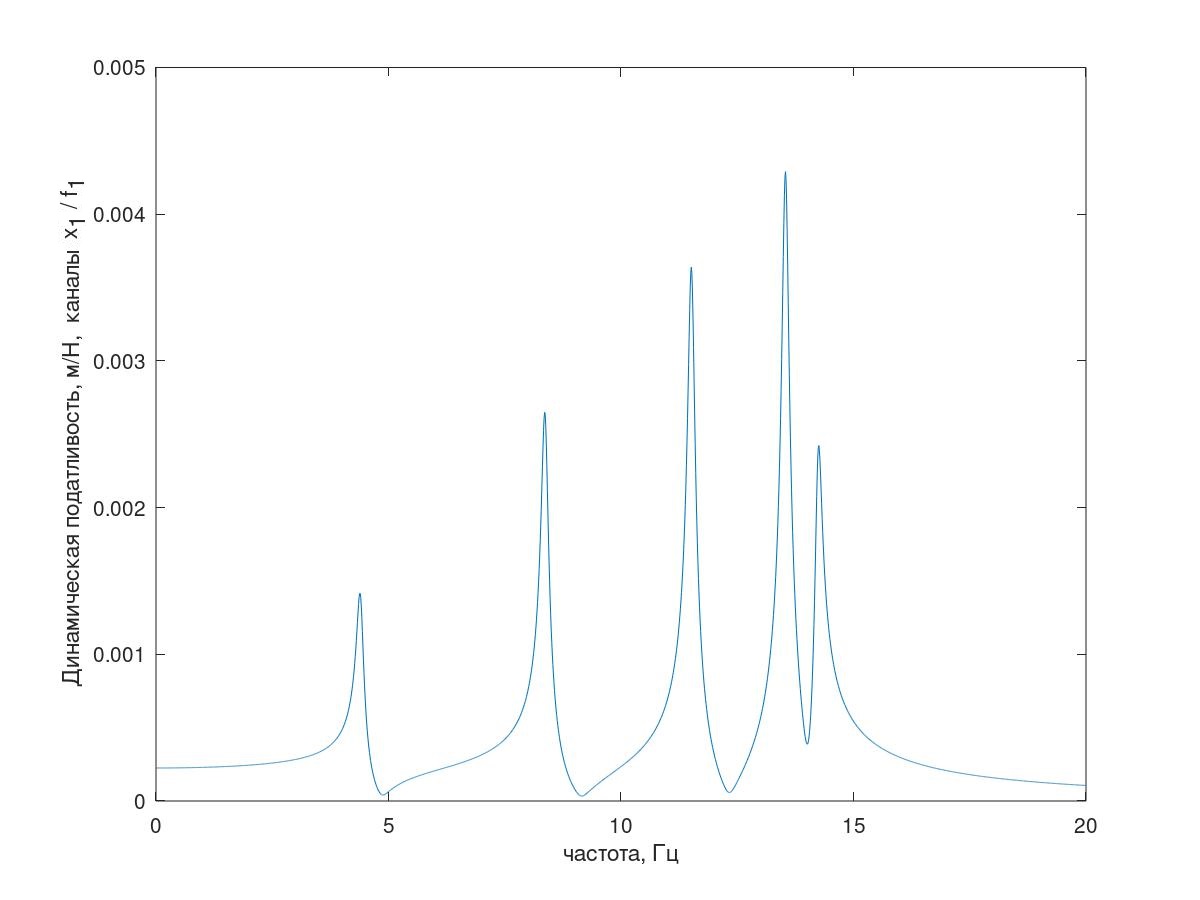图6五个共振的说明。
对于离散时间仿真，使用了有限差分模型（拉曼模型在较小的采样间隔下效果很好，
如图所示 ）。
一个小题外话。 一段时间后，在另一项工作的框架内，通过其他方式对该测试系统进行了有限差分建模（Xcos \ Simulink）。 在数学上，模型是相同的。 获得了系统对节点No 1和No 3的单次脉冲响应的动画图像。 从验证有限差分模型的角度来看，这里的结果很有趣。
（自由软件帧的“不可预测的”缓冲会稍微破坏图像，尤其是第二个图像，但从原理上讲，结果是非常好的。）
回到我们的Matlab（GNUOctave）模型。 产生的响应频谱如图7所示。
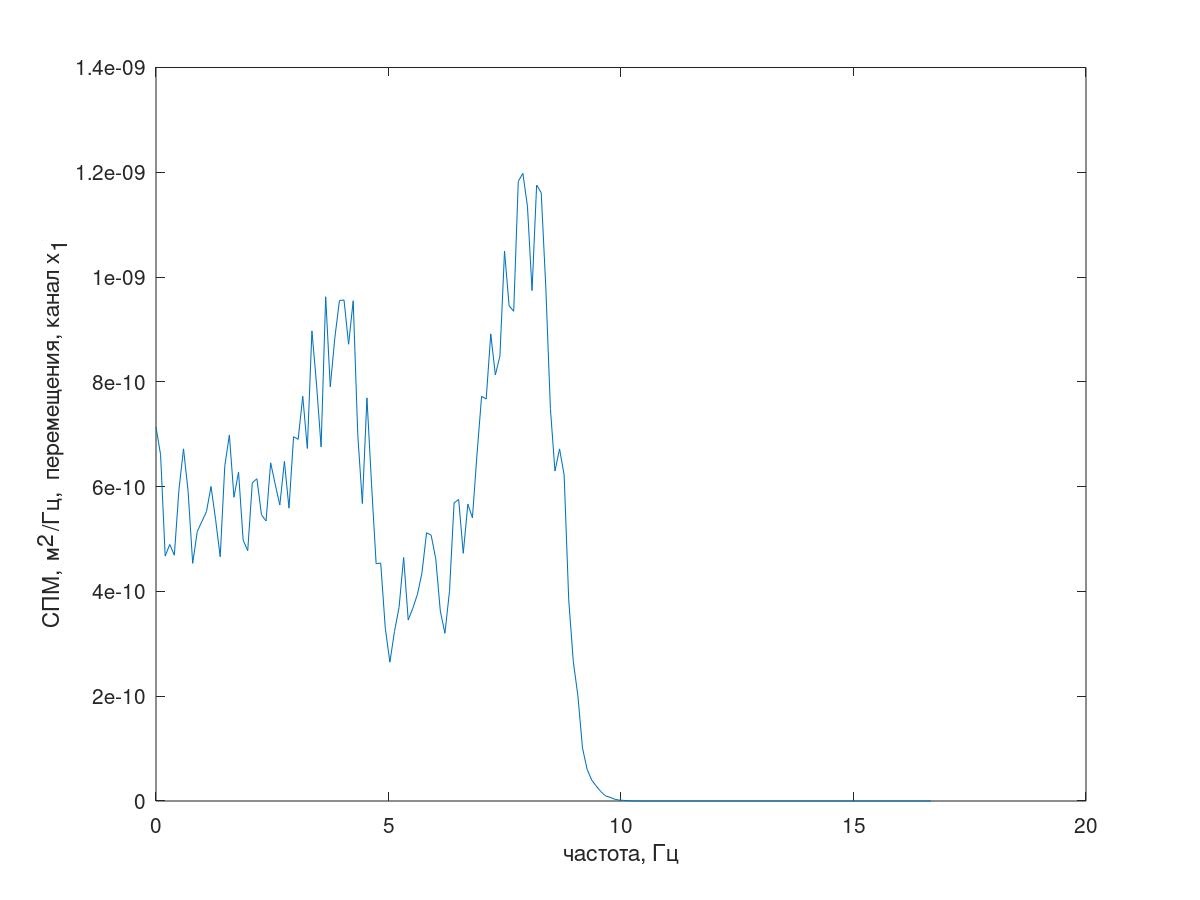图7响应频谱（通道x 1 ）此外，使用相关方法来找到响应通道的自相关和互相关值。
应用讨论中的方法的结果：发现伪模态过程Rqq的变异和H的伪明显形式：
分解中的前三个过程，整个多通道过程的动画以及32个样本（从6714个样本到6746个样本，即从67.13 s的数量）中相应的前三个振动模式显然在数量上有意义（根据它们在Rqq中的分散值）本文开头的图1中显示了67.63 s的当前时间）。 如您所见，这些伪形式与它们自己的弦振动形式有一些相似之处。
积累的经验表明该方法具有以下特点。
- 该方法对外部噪声敏感，包括 高频率。 存在获得“随机”结果（具有较大的随机误差）的危险，并且实验结果具有明显的不可重复性。 必须仔细滤除多通道信号频率范围的无效部分（在数量上微不足道）。 （有一次，由于实验者报道通道之间“不存在”相关性（强噪声的影响），甚至停止了该方向的工作。）
- 当观察通道的数量明显大于振动形式的预期表现形式（研究范围内的共振峰数量）时，即获得最佳结果。 对于m << n。
- 在高Q因子的情况下，伪形式系统似乎倾向于系统的真实本征模。 在出现噪音的情况下，在此类系统上获得的结果更加稳定。
- 如果一对特征值Rxx [0]一致甚至收敛，则显然要确定一对相应的伪形式，直到它们独立的线性组合-在给定的实验条件下，这些形式之间不能分开。
- 显然，比较实际的形式（通过其他方法找到的形式）和所考虑的伪形式，如果这样的问题是相关的，则有可能找到外部扰动的应用点（特别是对于小通道扰动）。