😭 ◻️ 👵🏿 小波分析。基础知识 🕓 🏤 👨🏻‍🍳

引言

英语单词wavelet（来自法语“ ondelette”）字面翻译为“短（小）波”。在将外国文章翻译成俄文的各种翻译中，也有一些术语：“爆发”，“爆发功能”，“低波功能”，“波”等。

小波变换（VP）广泛用于信号分析。另外，它在数据压缩领域也有很大的应用。一维信号的VP是在基函数系统上以广义级数或傅立叶积分的形式表示的。

p s i_{a b} （ t ） = f r a c 1 s q r t a p s i l e f t （ f r a c t - b a r i g h t ）

$\ psi _ {ab}（t）= \ frac {1} {\ sqrt {a}} \ psi \ left（\ frac {t-b} {a} \ right）$ ，（1）

从母亲（源）小波构造

p s i （ 吨 ）

$\ psi（吨）$ 由于时移操作（b）和时标变化（a）而具有某些属性。

乘数

1 / s q r t a

$1 / \ sqrt {a}$ 确保函数规范（1）与缩放数（a）的独立性。对于参数a和b的给定值，该函数

p s i_{a b} （ t ）

$\ psi_ {ab}（t）$ 母小波产生了一个小波

p s i （ 吨 ）

$\ psi（吨）$ 。

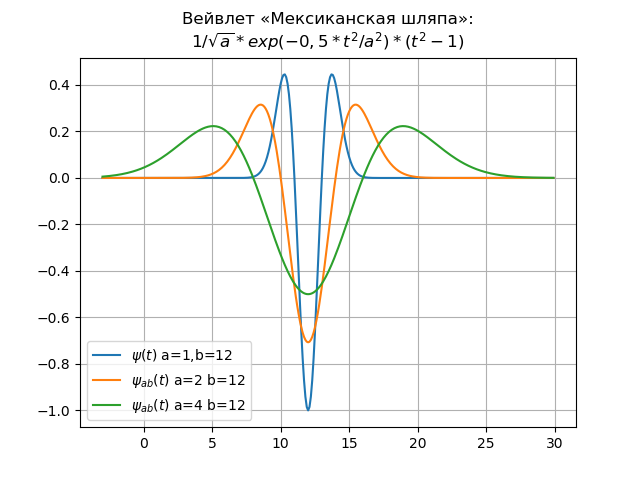
一个示例是时域和频域中的墨西哥帽小波：

时域的小波列表

from numpy import* import matplotlib.pyplot as plt x= arange(-4,30,0.01) def w(a,b,t): f =(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1) return f plt.title(" « »:\n$1/\sqrt{a}*exp(-0,5*t^{2}/a^{2})*(t^{2}-1)$") y=[w(1,12,t) for t in x] plt.plot(x,y,label="$\psi(t)$ a=1,b=12") y=[w(2,12,t) for t in x] plt.plot(x,y,label="$\psi_{ab}(t)$ a=2 b=12") y=[w(4,12,t) for t in x] plt.plot(x,y,label="$\psi_{ab}(t)$ a=4 b=12") plt.legend(loc='best') plt.grid(True) plt.show()

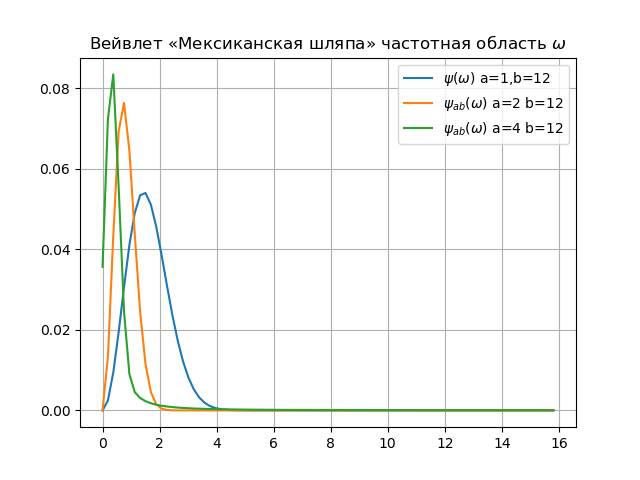
小波频谱清单

 from numpy import* from pylab import * from scipy import * import os def w(a,b,t): f =(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1) return f x= arange(-4,30,0.2) def plotSpectrum(y,Fs): n = len(y) k = arange(n) T = n/Fs frq = k/T frq = frq[range(int(n/2))] Y = fft(y)/n Y = Y[range(int(n/2))] return Y,frq xlabel('f (Hz)') ylabel('|Y(f)|') Fs=1024.0 y=[w(1,12,t) for t in x] Y,frq=plotSpectrum(y,Fs) plot(frq,abs(Y),label="$\psi(\omega)$ a=1,b=12") y=[w(2,12,t) for t in x] Y,frq=plotSpectrum(y,Fs) plot(frq,abs(Y),label="$\psi_{ab}(\omega)$ a=2 b=12") y=[w(4,12,t) for t in x] Y,frq=plotSpectrum(y,Fs) plot(frq,abs(Y),label="$\psi_{ab}(\omega)$ a=4 b=12") plt.title(" « »   $\omega$") legend(loc='best') grid(True) show()

结论：

1.在傅立叶谐波的概念和小波的尺度之间，确实存在关系。这种关系中最主要的是自然频率和比例的反比例。另外，减小尺度，我们增加了小波谱的带宽。

2.通过更改比例（增大a会导致函数的傅立叶谱变窄

p s i_{a b} （ t ）

$\ psi_ {ab}（t）$ ），小波能够检测到不同尺度（频率）上的特征差异，并且由于偏移，可以在整个研究区间的不同点分析信号特性。因此，在分析非平稳信号时，由于小波的局部性，它们相对于傅立叶变换具有明显的优势，傅立叶变换仅给出有关所分析信号的频率（标度）的全局信息，因为所使用的函数系统（复指数或正弦和余弦）是在无限间隔。

3.以上以自由发行的高级Python语言编写的清单允许您选择满足指定要求的小波函数。但是，还必须考虑小波的所有主要符号。

小波的主要迹象

局限性。 函数范数的平方必须是有限的：

\左 | p s i \右 |^{2} = i n t_{- i n f t y}^{i n f t y} \左 | p s i （ t ） \右 |^{2} d t < i n f t y

$\左\ | \ psi \右\ | ^ {2} = \ int _ {-\ infty} ^ {\ infty} \左| \ psi（t）\右| ^ {2} dt <\ infty$ 。（2）

本地化 与傅立叶变换相反，VP在时间和频率上都使用局部初始函数。为此，满足条件就足够了：

\左 | p s i （ t ） \右 | l e q C （ 1 + \左 | t \右 | ）^{- 1 - v a r e p s i l o n}

$\左| \ psi（t）\右| \ leq C（1+ \左| t \右|）^ {-1- \ varepsilon}$ 和

\左 | S_{p s i} （ o m e g a ） \右 | l e q C （ 1 + \左 | o m e g a \右 | ）^{- 1 - v a r e p s i l o n}

$\左| S _ {\ psi}（\ omega）\右| \ leq C（1+ \左| \ omega \右|）^ {-1- \ varepsilon}$ 在

v a r e p s i l o n > 0

$\ varepsilon> 0$ ，（3）

例如，增量功能

\增 量 （ t ）

$\增量（t）$ 和谐波函数不能满足时域和频域同时定位的必要条件。

零平均值。 原始函数的图应在时间轴上围绕零振荡（交替），并具有零面积：

i n t_{- i n f t y}^{i n f t y} p s i （ t ） d t = 0

$\ int _ {-\ infty} ^ {\ infty} \ psi（t）dt = 0$ 。（4）

从这种情况下，可以清楚地选择“小波”的名称-小波。

等于零功能区

p s i （ 吨 ）

$\ psi（吨）$ ，即零矩，导致傅立叶变换

S_{p s i} （ o m e g a ）

$S _ {\ psi}（\ omega）$ 该函数等于零

o m e g a = 0

$\ omega = 0$ 并具有带通滤波器的形式。对于各种值（a），这将是一组带通滤波器。

通常，对于应用程序，不仅有必要使零，而且所有前n个矩都必须等于零：

i n t_{- i n f t y}^{i n f t y} t^{^{n}} p s i （ t ） d t = 0

$\ int _ {-\ infty} ^ {\ infty} t ^ {^ {n}} \ psi（t）dt = 0$ 。（5）

第n个子波可以分析信号的更精细（高频）结构，从而抑制其缓慢变化的分量。

自制的。 VP的一个特征是它的自相似性。特定家庭的所有小波

p s i_{a b} （ t ）

$\ psi_ {ab}（t）$ 振荡次数与母小波相同

p s i （ 吨 ）

$\ psi（吨）$ ，因为它是通过比例变换（a）和平移（b）从中获得的。

连续小波变换

连续（积分）小波变换（NVP或WT-连续小波变换）。我们建立基础

p s i_{a b} （ t ）

$\ psi_ {ab}（t）$ 使用母子波的连续尺度变换（a）和传递（b）

p s i （ 吨 ）

$\ psi（吨）$ 在公式（1）中具有基本参数a和b的任意值。

然后，根据定义，信号S（t）的正向（分析）和反向（合成）NVP（即PNVP和ONVP）编写如下：

W_{s} （ a ， b ） = （ S （ t ） ， p s i_{a b} （ t ） ） = f r a c 1 s q r t a i n t_{- i n f t y}^{i n f t y} S （ t ） p s i \左 （ f r a c t b a \右 ） d t

$W_ {s}（a，b）=（S（t），\ psi _ {ab}（t））= \ frac {1} {\ sqrt {a}} \ int _ {-\ infty} ^ {\ infty} S（t）\ psi \左（\ frac {tb} {a} \右）dt$ ，（6）

S （ t ） = f r a c 1 C_{p s i} i n t_{- i n f t y}^{i n f t y} i n t_{- i n f t y}^{i n f t y} W_{s} （ a ， b ） p s i_{a b} （ t ） f r a c d a d b a^{2}

$S（t）= \ frac {1} {C _ {\ psi}} \ int _ {-\ infty} ^ {\ infty} \ int _ {-\ infty} ^ {\ infty} W_ {s}（a，b ）\ psi _ {ab}（t）\ frac {dadb} {a ^ {2}}$ ，（7）

在哪里

C_{p s i}

$C _ {\ psi}$ -归一化系数，

C_{p s i} = i n t_{- i n f t y}^{i n f t y} \左 | p s i （ o m e g a ） \右 |^{2} \左 | o m e g a \对 |^{- 1} d o m e g a < i n f t y

$C _ {\ psi} = \ int _ {-\ infty} ^ {\ infty} \左| \ psi（\ omega）\右| ^ {2} \左| \ omega \对| ^ {-1} d \ omega <\ infty$
其中：（•，•）是相应因子的标量积，

m a t h b f p s i （ o m e g a ）

$\ mathbf {\ psi（\ omega）}$ -小波的傅立叶变换

p s i （ 吨 ）

$\ psi（吨）$ 。对于正交小波

C_{p s i} = 1

$C _ {\ psi} = 1$ 。

从（6）可知，小波谱

W_{s} （ b ， a ）

$W_ {s}（b，a）$ （小波频谱或时标频谱）不同于傅立叶频谱（单频谱），它是两个自变量的函数：第一个自变量a（时间标度）类似于振荡周期，即与频率成反比，第二个b –与沿时间轴的信号偏移相似。

应该注意的是

W_{s} （ b ， a_{0} ）

$W_ {s}（b，a_ {0}）$ 表征时间依赖性（在

a = a_{0} ）

$a = a_ {0}）$ ，而依赖项

W_{s} （ a ， b_{0} ）

$W_ {s}（a，b_ {0}）$ 可以匹配频率依赖性（对于

b = b_{0}

$b = b_ {0}$ ）

如果研究信号S（t）是持续时间的单个脉冲

t a u_{u}

$\ tau_ {u}$ 集中在附近

t = t_{0}

$t = t_ {0}$ ，则其小波谱将在具有坐标的点附近具有最大值

a = t a u_{u} ， b = t_{0}

$a = \ tau_ {u}，b = t_ {0}$ 。

演示方法

W_{s} （ b ， a ）

$W_ {s}（b，a）$ 可能有所不同。频谱图

W_{s} （ b ， a ）

$W_ {s}（b，a）$ 是三维空间中的曲面。但是，通常不是等值于表面的图像，而是等值线（或各种颜色的图形）显示了它在ab平面上的投影，这使得可以跟踪不同比例（a）和时间（b）的EP振幅强度的变化。

此外，它们还描绘了这些表面的局部极值线，即所谓的骨架（塞尔顿），它揭示了所分析信号的结构。

在基于母子波（“墨西哥帽”）确定子波频谱时，进行连续子波变换。

还使用了其他用于NVP的孕妇小波：

连续VP广泛用于信号处理。特别是，小波分析（VA）提供了独特的机会来识别信号（功能）的局部和“细微”特征，这在无线电工程，通信，无线电电子，地球物理学和其他科学和技术领域的许多领域都非常重要。让我们通过一些简单的例子来考虑这种可能性。

谐波振荡。

信号具有以下形式：

s （ t ） = 阿 辛 （ o m e g a t - p h i ）

$s（t）=阿辛（\ omega t- \ phi）$

其中：

A = 1 V ， o m e g a = f r a c 2 p i T = f r a c 2 p i 50 ， p s i = 0

$A = 1 V，\ omega = \ frac {2 \ pi} {T} = \ frac {2 \ pi} {50}，\ psi = 0$

小波形成功能：

M H A T （ t ） ： = f r a c d^{2} d t^{2} e x p （ - t^{2} / 2 ）

$MHAT（t）：= \ frac {d ^ {2}} {dt ^ {2}} exp（-t ^ {2} / 2）$ ，

小波：

p s i （ a ， b ， t ） = f r a c 1 s q r t a 左 侧 （ f r a c t - b a r i g h t ）

$\ psi（a，b，t）= \ frac {1} {\ sqrt {a}}左侧\\（frac {t-b} {a} \ right）$ ，

小波谱：N：= 256，a：= 1..30，b：= 0..50，

W （ a ， b ） ： = i n t_{- N}^{N} p s i （ a ， b ， t ） s （ t ） d t ， N_{a b} ： = W （ a ， b ）

$W（a，b）：= \ int _ {-N} ^ {N} \ psi（a，b，t）s（t）dt，N_ {ab}：= W（a，b）$ 。

程序清单

 from scipy.integrate import quad from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm N=256 T=50 def S(t): return sin(2*pi*t/T) plt.figure() plt.title('  ', size=12) y=[S(t) for t in arange(0,100,1)] x=[t for t in arange(0,100,1)] plt.plot(x,y) plt.grid() def w(a,b): f = lambda t :(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1)*S(t) r= quad(f, -N, N) return round(r[0],3) x = arange(1,50,1) y = arange(1,50,1) z = array([w(i,j) for j in y for i in x]) X, Y = meshgrid(x, y) Z = z.reshape(49,49) fig = plt.figure("- :  ") ax = Axes3D(fig) ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel(' :a') ax.set_ylabel(': b') ax.set_zlabel(' : $ N_{ab}$') plt.figure("2D-  z = w (a,b)") plt.title(' ab    ', size=12) plt.contourf(X, Y, Z,100) plt.show()

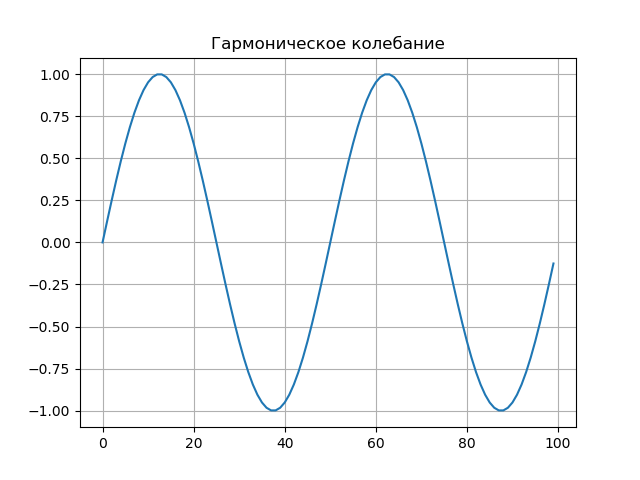
信号图。

两参数光谱图

N_{a b} = W （ a b ）

$N_ {ab} = W（ab）$ 在三维空间中显示为曲面。

应当注意的是，时标的W（a，b）节

a = a_{0}

$a = a_ {0}$ 表征初始振荡s（t）。而且，它的振幅在

a_{0} ： 1 / o m e g a

$a_ {0}：1 / \ omega$ 。依存关系

W （ a_{0} ， b_{0} ）

$W（a_ {0}，b_ {0}）$ 可以匹配当前的振荡频谱

b = b_{0}

$b = b_ {0}$ 。

两次谐波振荡的总和。

信号具有以下形式：

s （ t ） ： = A_{1} s i n （ o m e g a_{1} t ） + A_{2} s i n （ o m e g a_{2} t ）

$s（t）：= A_ {1} sin（\ omega _ {1} t）+ A_ {2} sin（\ omega _ {2} t）$

其中：

A_{1} = A_{2} = 1 V ， o m e g a_{1} = f r a c 2 p i T_{1} ， o m e g a_{2} = f r a c 2 p i T_{2} ， T_{1} = 50 秒 ， T_{2} = 10 秒

$A_ {1} = A_ {2} = 1V，\ omega_ {1} = \ frac {2 \ pi} {T_ {1}}，\ omega_ {2} = \ frac {2 \ pi} {T_ {2 }}，T_ {1} = 50秒，T_ {2} = 10秒$ 。

M H A T （ t ） ： = f r a c d^{2} d t^{2} \左 [e^{- t^{2 / 2}} \右]

$MHAT（t）：= \ frac {d ^ {2}} {dt ^ {2}} \左[e ^ {-t ^ {2/2}} \右]$ ，N：= 256，

p s i （ a ， b ， t ） ： = 哪 一 个 \左 （ f r a c t b a \右 ） ， W （ a ， b ） ： = i n t_{- N}^{N} p s i （ a ， b ， t ） f （ t ） d t

$\ psi（a，b，t）：=哪一个\左（\ frac {tb} {a} \右），W（a，b）：= \ int _ {-N} ^ {N} \ psi（a ，b，t）f（t）dt$ ，a：= 1 ... 30，b：= 0 ... 50，

N_{a b} ： = W （ a ， b ）

$N_ {ab}：= W（a，b）$ 。

程序清单

 from scipy.integrate import quad from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm N=256 def S(t): return sin(2*pi*t/10)+sin(2*pi*t/50) plt.figure('    ') plt.title('    ', size=12) y=[S(t) for t in arange(0,250,1)] x=[t for t in arange(0,250,1)] plt.plot(x,y) plt.grid() def w(a,b): f = lambda t :(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1)*S(t) r= quad(f, -N, N) return round(r[0],3) x = arange(1,50,1) y = arange(1,50,1) z = array([w(i,j) for j in y for i in x]) X, Y = meshgrid(x, y) Z = z.reshape(49, 49) fig = plt.figure("-:2-  ") ax = Axes3D(fig) ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel(' :a') ax.set_ylabel(': b') ax.set_zlabel(' : $ N_{ab}$') plt.figure("2D-  z = w (a,b)") plt.title(' ab    ', size=12) plt.contourf(X, Y, Z, 100) plt.figure() q=[w(2,i) for i in y] p=[i for i in y] plt.plot(p,q,label='w(2,b)') q=[w(15,i) for i in y] plt.plot(p,q,label='w(15,b)') q=[w(30,i) for i in y] plt.plot(p,q,label='w(30,b)') plt.legend(loc='best') plt.grid(True) plt.figure() q=[w(i,13) for i in x] p=[i for i in x] plt.plot(p,q,label='w(a,13)') q=[w(i,17) for i in x] plt.plot(p,q,label='w(a,17)') plt.legend(loc='best') plt.grid(True) plt.show()

信号图。

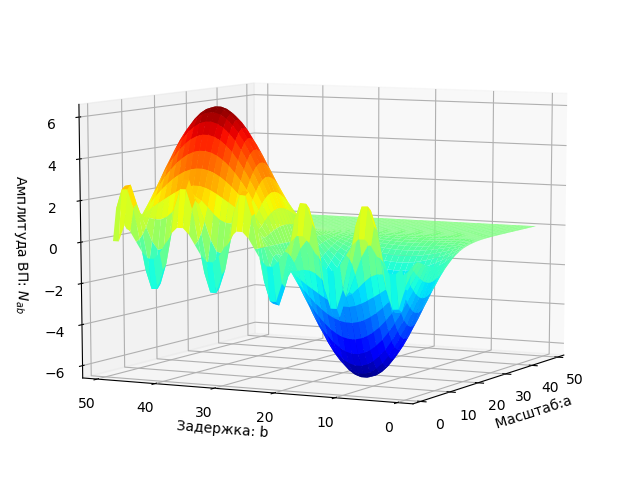
两参数频谱W（a，b）的图显示为三维空间中的曲面。

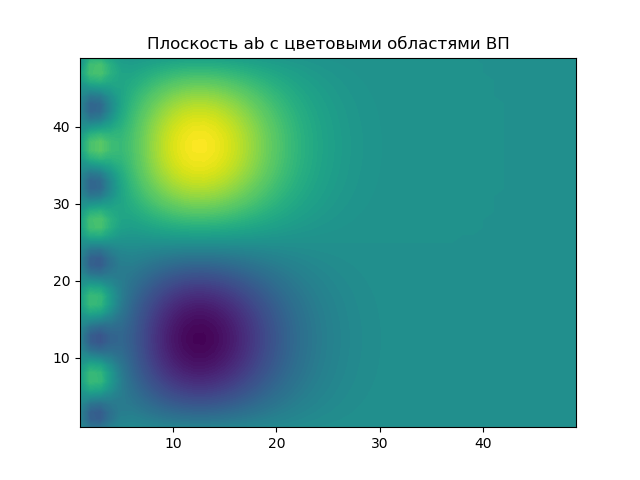
EP的结果在彩色区域中突出显示参数a，b的平面。

该图显示了参数a的两个值的小波谱的“横截面”。使用相对较小的时间标度a

a_{1} = 2 （ a_{1} ： 1 / o m e g a_{2} ）

$a_ {1} = 2（a_ {1}：1 / \ omega_ {2}）$ ，频谱的横截面仅携带有关信号高频分量的信息，从而滤出（抑制）其低频分量。

随着增加，基函数的扩展

p s i （ f r a c t - b a ）

$\ psi（\ frac {t-b} {a}）$ 因此，会缩小其频谱，并缩小频率“窗口”的带宽。结果，当

a_{2} = 15 （ a_{2} ： 1 / o m e g a_{1} ）

$a_ {2} = 15（a_ {2}：1 / \ omega_ {1}）$ 频谱的横截面只是信号的低频成分。

随着a的进一步增加，窗带仍然减小，并且该低频分量的电平减小到恒定分量（对于a> 25），对于分析的信号等于零。

该图显示了表征小波频谱W（a，b）的部分
当前信号频谱

b_{1} = 13

$b_ {1} = 13$ 和

b_{2} = 17

$b_ {2} = 17$ 。与谐波相比，所考虑信号的频谱在时间标度a（a：1..3）的较小值区域中包含一个高频分量，它对应于信号的第二分量

A_{2} 罪 （ o m e g a_{2} t ）

$A_ {2}罪（\ omega_ {2} t）$ 。

矩形动量。

U ： = 5 ， t_{0} ： = 20 ， t a u ： = 60

$U：= 5，t_ {0}：= 20，\ tau：= 60$

s （ t ） ： = \开 始 v m a t r i x U ， 如 果 t_{0} l e q t l e q t_{0} + t a u 0 ， 否 则 e n d v m a t r i x

$s（t）：= \开始{vmatrix} U，如果t_ {0} \ leq t \ leq t_ {0} + \ tau \\ 0，否则\ end {vmatrix}$

M H A T （ t ） ： = f r a c d^{2} d t^{2} e x p \左 （ f r a c - t^{2} 2 \右 ）

$MHAT（t）：= \ frac {d ^ {2}} {dt ^ {2}} exp \左（\ frac {-t ^ {2}} {2} \右）$

N ： = 128 ， p s i （ a ， b ， t ） ： = M H A T \左 （ f r a c t b a \右 ） ， W （ a ， b ） ： = i n t_{- N}^{N} p s i （ a ， b ， t ） f （ t ） d t

$N：= 128，\ psi（a，b，t）：= MHAT \左（\ frac {tb} {a} \右），W（a，b）：= \ int _ {-N} ^ {N } \ psi（a，b，t）f（t）dt$

a ： = 1..50 ， b ： = 0..100 ， N_{b a} ： = W （ a ， b ）

$a：= 1..50，b：= 0..100，N_ {ba}：= W（a，b）$

程序清单

 from scipy.integrate import quad from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm N=256 def S(t): U=5;t0=20;tau=60 if t0<=t<=t0+tau: return U else: return 0 plt.figure() plt.title(' ', size=12) y=[S(t) for t in arange(0,120,1)] x=[t for t in arange(0,120,1)] plt.plot(x,y) plt.grid() def w(a,b): f = lambda t :(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1)*S(t) r= quad(f, -N, N) return round(r[0],3) x = arange(1,100,1) y = arange(1,100,1) z = array([w(i,j) for j in y for i in x]) X, Y = meshgrid(x, y) Z = z.reshape(99, 99) fig = plt.figure("3D-  ") ax = Axes3D(fig) ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel(' :a') ax.set_ylabel(': b') ax.set_zlabel(' : $ N_{ab}$') plt.figure("2D-  z = w (a,b)") plt.title(' ab    ', size=12) plt.contourf(X, Y, Z,100) plt.show()

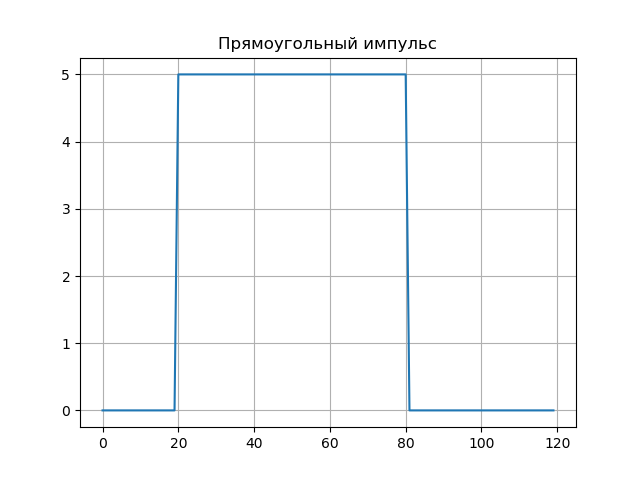
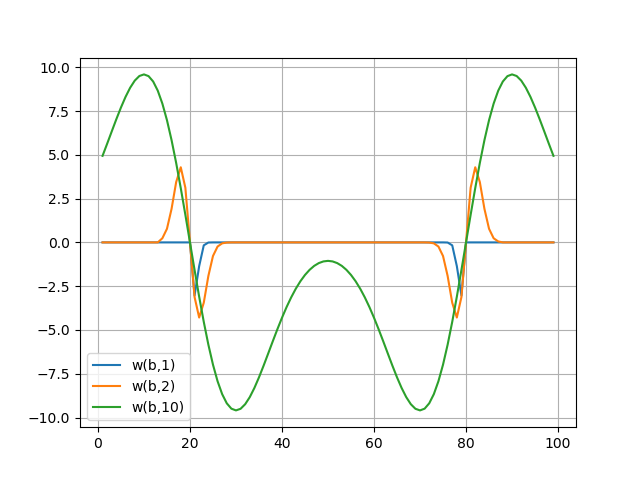
小波频谱如图所示，小波频谱很好地传达了信号的微妙特征-其在样本b = 20和b = 80上的跳跃（对于a：1..10）。

结论

该出版物本质上是教育性的，它提供了有关小波分析的基本信息，而自由分发的高级编程语言Python中的简单示例显示了具有广泛的图形3D和2D可视化的连续小波分析的功能。

PS作者在小波数量和速度方面都没有减损使用Matlab进行小波分析的无条件优势。但是在Python中，仍有进一步开发的空间：scipy.signal和PyWavelets。

小波分析。 基础知识

引言

小波的主要迹象

连续小波变换

在基于母子波（“墨西哥帽”）确定子波频谱时，进行连续子波变换。

结论

More articles:

小波分析。基础知识