IT行业的每个人都知道评估项目截止日期有多么困难 。 很难客观地评估解决一个困难的任务需要多长时间。 我最喜欢的理论之一是，这只是统计伪像。

假设您在1周时评估了一个项目。 假设有三个同样可能的结果：将需要1/2周，1周或2周。 中位数结果实际上与估算值相同：1周，但平均值（也就是平均值，也就是预期值）为7/6 = 1.17周。 该分数实际上是针对中位数（即1）进行了校准（特别是），而不是针对平均值进行了校准。

合理的“通货膨胀因子”模型（实际时间除以估计时间）将类似于对数正态分布 。 如果估计值等于一周，则我们将真实结果模拟为一个随机变量，该随机变量按照对数正态分布分布约一周。 在这种情况下，分布的中位数恰好是一周，但平均值要大得多：



如果我们采用通货膨胀系数的对数，我们将得到一个简单的正态分布，其中心大约为0。这假设通货膨胀系数的中位数为1x，并且如您所愿，请记住，log（1）=0。但是，在各种问题中，0附近的不确定性可能不同。我们可以通过更改参数σ来建模，该参数对应于正态分布的标准偏差：



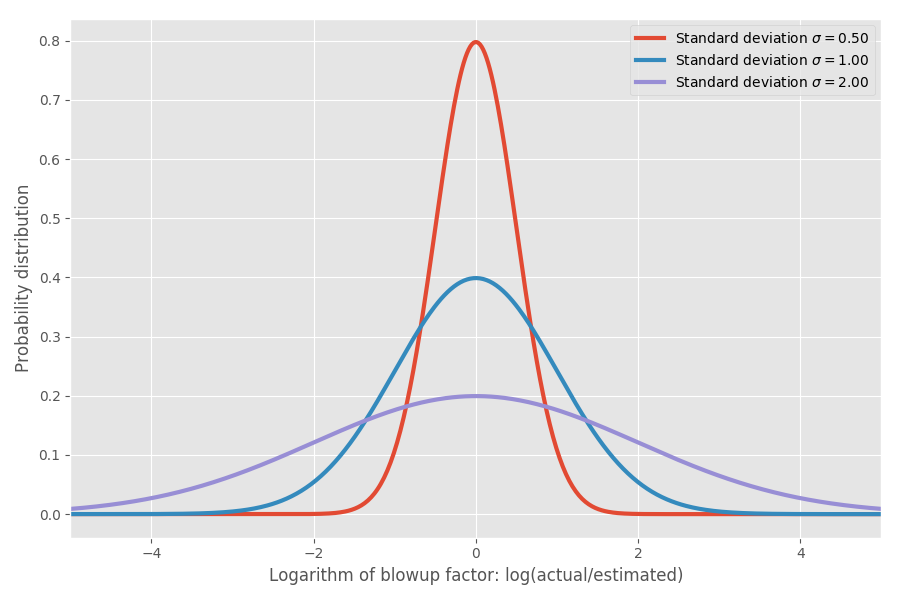
仅显示实数：当log（实际/估计）= 1时，通胀系数exp（1）= e = 2.72。 同样有可能项目将扩展为exp（2）= 7.4倍，并且项目将以exp（-2）= 0.14结束，即估计时间的14％。 直观上，平均值之所以如此之大是因为运行速度比预期快的任务无法补偿花费比预期长得多的任务。 我们限制为0，但不限于另一个方向。

这只是一个模特吗？ 希望你能！ 但是很快我将获得真实数据，并根据一些经验数据将证明实际上它与现实非常吻合。

估算软件开发时间表

到目前为止，一切都很好，但是让我们真正地尝试了解它在估计软件开发时间表方面的意义。 假设我们研究了一个由20个不同软件项目组成的计划，并尝试评估完成所有这些软件将花费多长时间。

这就是平均值成为决定性因素的地方。 平均值加起来，但没有中位数。 因此，如果我们想了解完成N个项目的总和需要多长时间，则需要查看平均值。 假设我们有三个不同的项目，它们的σ= 1：


请注意，平均值加起来为4.95 = 1.65 * 3，但其他列则不然。

现在，我们添加三个具有不同sigma的项目：


平均数仍在形成中，但实际情况甚至还不接近您可能期望的3周天真估计。 请注意，σ= 2的高度不确定的项目在平均完成时间中占主导地位 。 对于第99个百分位数，它不仅占主导地位，而且实际上吸收了所有其他百分比。 我们可以举一个更大的例子：


同样，至少在99％的情况下，唯一不愉快的任务主要是在估算的计算中占主导地位。 即使在平均时间上，一个疯狂的项目最终也要花费大约一半的时间在所有任务上，尽管它们的中值相似。 为简单起见，我假设所有任务的时间估计都相同，但不确定性不同。 术语更改时将保存数学。

很有趣，但是我很早就有这种感觉。 当您有很多任务时，添加评分很少会起作用。 相反，找出不确定性最高的任务：这些任务通常将主导平均执行时间。

该图显示了平均值和第99个百分位数作为不确定性（σ）的函数：



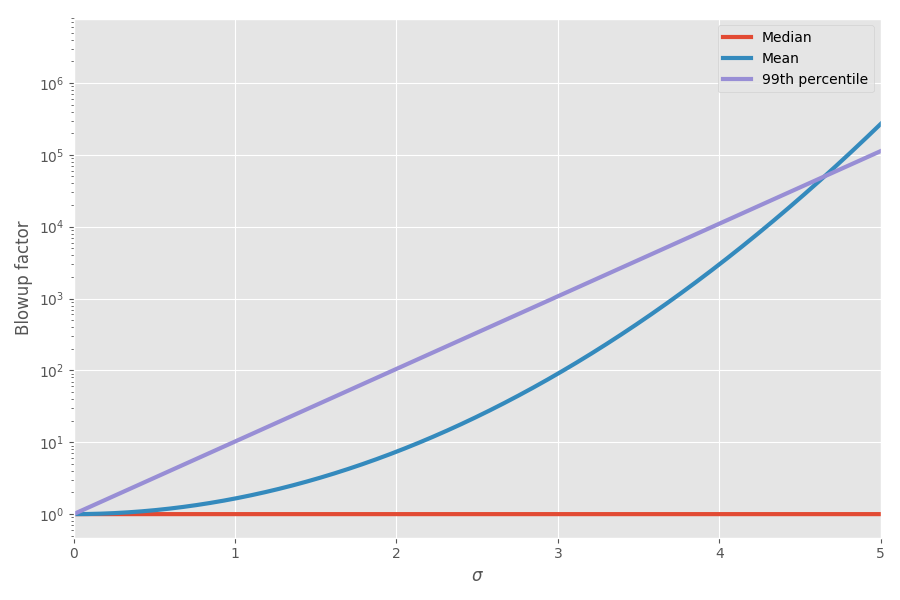
现在数学解释了我的感觉！ 在计划项目时，我开始考虑到这一点。 我真的认为添加任务期限的估计值非常容易产生误导，并且会错误地说明整个项目将花费多少时间，因为您有这些疯狂的，歪斜的任务最终会一直占用。

经验证据在哪里？

很长时间以来，我一直在“好奇的玩具模型”部分中将其保存在大脑中，有时认为这是对现实世界现象的巧妙说明。 但是有一天，我在网络上四处游荡，偶然发现了一组有趣的数据，用于评估项目的时间安排和完成项目的实际时间。 小说！

让我们快速制作一个估计和实际时间的散点图：



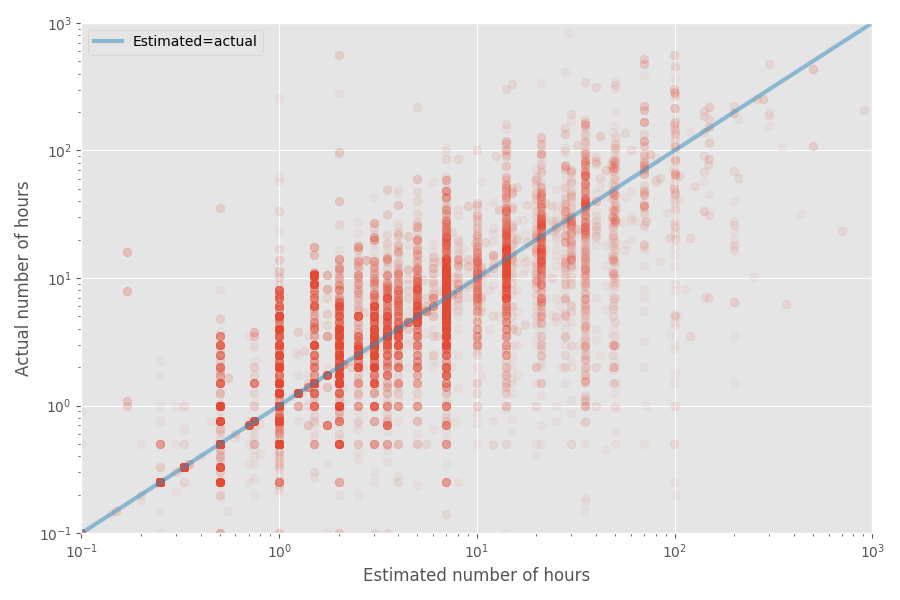
此数据集的中位数通胀率为1倍，而平均系数为1.81倍。 同样，这证实了开发人员对中位数的评价很好的预感，但平均值要高得多。

让我们看一下通货膨胀系数（对数）的分布：



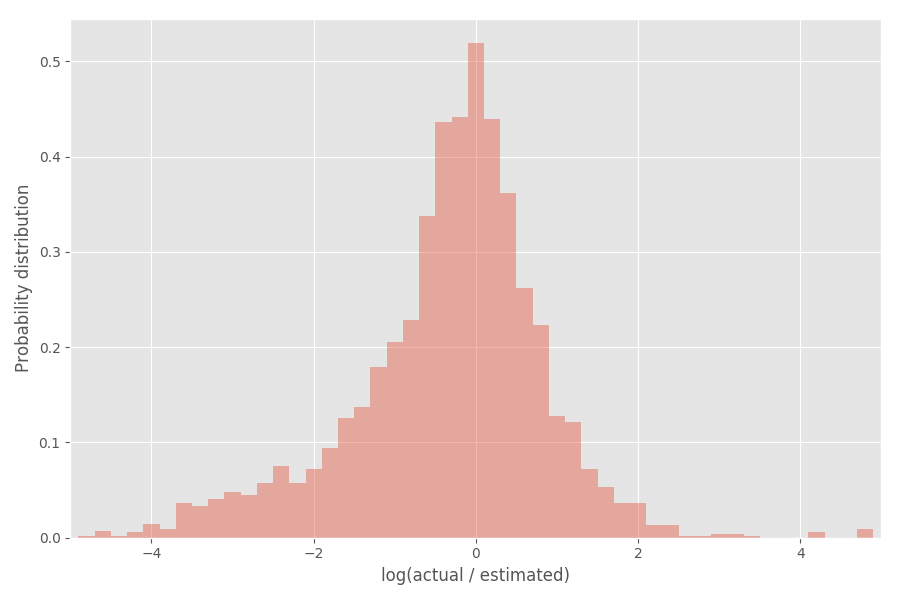
如您所见，它很好地位于0的中心，其中通胀系数exp（0）= 1。

采取统计工具

现在，我将对统计数据有所幻想-如果您觉得这部分内容不感兴趣，请立即跳过此部分。 从这种经验分布中我们可以得出什么结论？ 您可以预期通货膨胀率的对数将根据正态分布进行分布，但这并非完全正确。 请注意，σ本身是随机的，并且随每个项目而变化。

对σ建模的一种简便方法是从反伽马分布中选择它们。 如果我们假设（与以前一样）通货膨胀系数的对数是根据正态分布分布的，那么通货膨胀系数对数的“全局”分布以学生分布结尾。

我们将学生分配应用于上一个分配：



在我看来，相当不错！ 学生分布参数还确定σ值的反伽马分布：



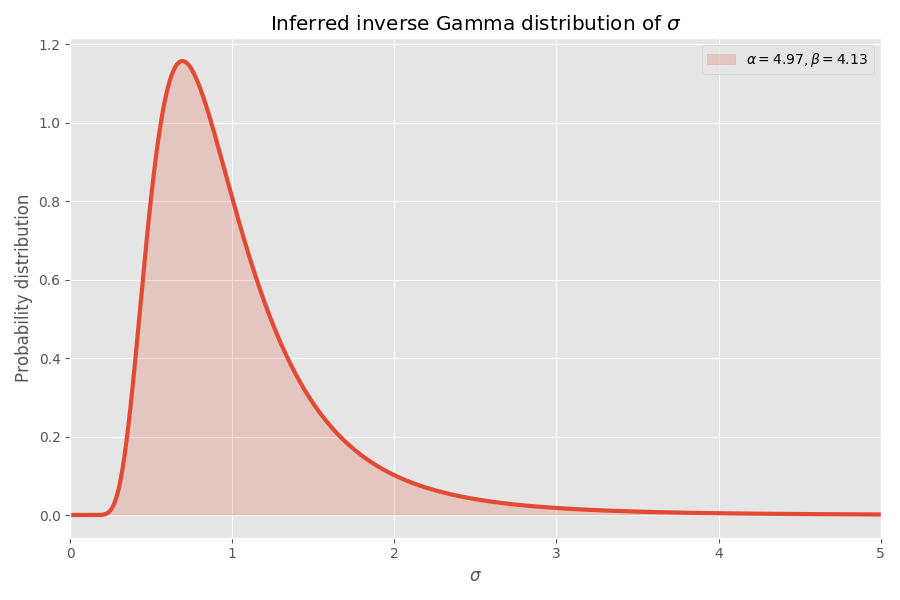
请注意，σ> 4的值不太可能，但是当它们出现时，它们会引起平均数千次爆炸。

为什么软件任务总是花费比您想象的更多的时间

假设该数据集代表软件开发（可疑！），我们可以得出更多结论。 我们有学生分布的参数，因此我们可以计算完成任务所需的平均时间，而无需知道此任务的σ。

尽管这次拟合的通货膨胀率中位数是1倍（和以前一样），但99％的通货膨胀率是32倍，但是如果您达到99.99个百分位，那将高达5500 万 ！ 一种（免费的）解释是，某些任务最终是不可能的。 实际上，这些极端情况对平均值产生巨大影响，以至于任何任务的平均通货膨胀率都是无限的 。 对于任何想按时完成任务的人来说，这都是一个坏消息！

总结

如果我的模型是正确的（如果是，则为大），这是我们可以发现的内容：

• 人们会很好地估计完成任务的中值时间，而不是平均时间。
  
• 由于分布失真（对数正态分布），因此平均时间比中位数大得多。
  
• 当您为n个任务添加分数时，情况会变得更糟。
  
• 不确定性最大的任务（而不是最大的任务）通常在完成所有任务所需的平均时间中占主导地位。
  
• 我们一无所知的任务的平均执行时间实际上是无限的 。

注意事项

• 显然，这些发现仅基于我在Internet上找到的一个数据集。 其他数据集可能会给出不同的结果。
  
• 我的模型当然也很主观，就像任何统计模型一样。
  
• 我很乐意将该模型应用于更大的数据集，以查看其稳定性。
  
• 我建议所有任务都是独立的。 实际上，它们可能具有相关性，这会使分析变得更加烦人，但是（我认为）最终得出的结论相似。
  
• 对数正态分布值的总和不是另一个对数正态分布值。 这是此分布的弱点，因为您可以说大多数任务只是子任务的总和。 如果我们的分布是可持续的 ，那就太好了。
  
• 我从直方图中删除了一些小任务（估计时间少于或等于7个小时），因为它们使分析失真，并且出现了恰好为7的怪异现象。
  
• 像往常一样， 代码在Github上 。