下午好，亲爱的读者！ 这是Chris Hecker撰写的有关创建物理引擎的系列文章中的第二篇翻译文章。 如果您尚未熟悉first ，那么我建议您这样做，因为一切都会立即变得清楚。 非常感谢您支持第一个翻译：继续努力是非常令人鼓舞的！ 祝您阅读愉快！

物理，第2部分，角度效应

我只是想用沉重的东西后门，以免入侵者进入。 我问很多吗？ 我希望他的车翻到特定位置并爆炸。 我希望大齿轮在压扁我之前先卡住。 我想匆忙建造一个看起来像秋千的东西，以便通过城堡的堡垒墙射出可爱的发光礼物。 谁能阻止我将所有这些变为现实？ 您假设我的对手在游戏世界中，但实际上-物理引擎的程序员，因为以上所有内容都是基于角度效应。 您可以指望那些实施了角点效果的游戏，更不用说找到至少一个可以正确完成这种效果的游戏了。

如今在游戏中未实现角度（或其他旋转）效果的主要原因是程序员认为描述旋转运动的物理学过于复杂，无法理解并转化为现实。 在高中的物理课中（我们都学过牛顿第二定律），他们通常不会谈论旋转效应，而且如何将施加于物体的力转变为物体的旋转还不是很明显。 当然，旋转运动的动力学比线性运动的动力学更难理解，但比看起来要简单。 可以根据周期的第一篇文章中介绍的材料创建物理引擎的任何人也将设法包括本文所述的角度效果。 希望在本文发表后，世界将充满利用角落效应的所有可能性和优势的游戏，或者至少您可以创建一个游戏，当您弯曲时，在致命的战斗中用腿射击朋友。

简短重复

尽管我的每篇文章都涉及一个独特的主题，但我始终会重新阅读我之前写的内容，以了解最终的结果。 我刚刚看了第一篇有关物理学的文章，我感到很高兴：我们学到了很多东西，而且，我们从未编写程序代码或阅读过其他文献！ 在开始之前，让我们刷新上一篇文章的内容。



表1包含了有关固体动力学的最重要结论。 从等式1可以得出，坐标矢量（r），速度矢量（v）和加速度矢量（a）与导数（和积分，如果我们以相反的顺序阅读）相关。 提醒一下，我们用质数（r'）标记时间差。 r'与dr / dt相同，并且r''与二阶导数相同。 从等式2可以得出，力与线性动量（质量与速度的乘积），质量和加速度相关。 质心的定义可以从等式3中获得（这是所有质量和距离彼此平衡的点）。 公式4指出，固体的总线性动量是其所有动量的总和，就我们的运气而言，它仅等于质心（CM）的动量。 公式5是真正的宝石。 它使用公式4证明对象的质心的加速度与标量即对象的质量的总力（在给定时间作用于对象的所有力之和的矢量）有关。

总结第一篇文章中描述的所有内容：我们了解到，作用在我们质心上的总力等于施加到身体上的所有力的总和（包括重力，小人的货车，附近的爆炸，引擎的推力等）。 ）。 之后，我们将该总和除以体重以获得CM加速度，然后对时间加速度进行积分以获得身体的速度和坐标。

方程式5只是杰作！ 您将看到其中没有对身体施加力的概念，这是确定身体在其作用下如何旋转的关键点。 等式5是正确的。 实际上，它对于找到线性加速度非常有用。 我们错过了一半的战斗。 但是首先要先...

你的角度是多少？

在第一篇文章中，旋转被忽略，因此我们只需要一个半径矢量及其导数来描述2D人体的构造。 现在，让我们添加另一个运动学值，方向（以大写字母Ω-Ω表示），以便使用转角效果。 为了设置Ω，我们需要选择相对于实体的坐标系和游戏世界的坐标系，并且Ω的值将等于它们之间的弧度角之差，如图1所示。



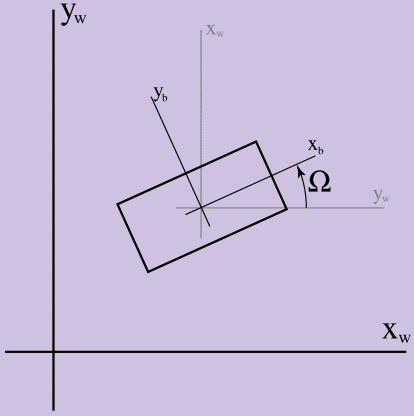图1.Ω的定义

在图中，xw，yw轴是游戏世界的坐标轴，而xb，yb是实体的坐标轴。 如果逆时针计数，则Ω大于0。 重要的是要澄清为什么我们要在转向三维之前研究二维世界的动力学：二维中的方向是一个标量（弧度的坐标系之间的角度），而确定三维世界中的方向要困难得多。

随着身体旋转，Ω的值改变。 这种变化将我们引向另一个运动学-角速度（用小写字母ω-ω表示）。 与物体的坐标和线速度相反，我们不将角速度表示为-Ω'。 但是，有时我们将速度相对于时间或角加速度的导数表示为ω'（这是另一个运动学值）或α（小写字母α）。 不要怪我：我没有提出所有这些称号； 在我读的每本书中都有细微的差异。 等式1的对应角为：

$$$$ display $$ {d ^ 2Ω\ over {dt ^ 2}} = {dω\ over {dt}} =ω'=α$$ display $$

方程式6

如公式1所示，我们在时间上微分ω以获得α。 通过对α的角加速度进行了解，我们可以对其进行两次积分以获得新的方向。 但是这里的关键是要知道α的值。

可以想像，本文的目标是为表1中的每个线性方程式得出一个角模拟量，然后考虑线性和角方程式以及施加到对象上的力，我们可以计算出其线性加速度a和角加速度α。 最后，我们可以对这些加速度进行数值积分，以找到我们身体的新位置和方向。

首先，我们将线性量和角度量连接在一起。 这是使用角速度的相当不明显的技巧。 在动力学计算中，我们经常需要找到对象上任意点的速度。 例如，当我们计算实体的碰撞时，我们需要知道碰撞点的速度，以便了解它们相互碰撞的程度。 如果我们的身体不旋转，则身体每个点的速度都相同。 我们可以简单地监视身体质心的速度，这就足够了。 如果我们的身体旋转，则这些身体的每个点都可以具有不同的速度。 显然，我们无法计算出刚体无限个点的速度，因此我们需要一个不同的更好的解决方案。

查找对象内部任意点的线速度的一种简单方法就是使用对象的角速度。 考虑以下情况：主体仅绕一个固定点O旋转，而不更改主体的坐标。 即，身体旋转，但是不移动。 从等式7，得出如何计算旋转体的B点的速度：

$$$$显示$$ v ^ B =ωr^ {OB}_⟂$$显示$$

式7

我们需要澄清公式7中的几点，让我们花一些时间在此上。 首先，我使用顶部索引来显示哪个参数属于这些点，因此v ^ B是人体B点的速度向量。 同样，r ^ OB表示从人体O的旋转中心到B点的向量。有趣的倒转字母T是作用于该向量上的“垂直算子”（如公式7中的向量r一样），并将其逆时针旋转90度。箭头。 换句话说，构建了一个垂直于旧矢量的新矢量。 在二维世界中，垂直于（x，y）的向量就是（-y，x）。 您可以轻松地在方格纸上检查我的话。 让我们更多地谈论这个。 垂直矢量的大小由角速度ω决定，并设置线速度v ^B。 用俄语表示，公式7表明，旋转体点的速度是通过将从旋转中心得出的垂直矢量乘以角速度来计算的。 我怎么理解？ 好吧，我在书中读过它，但是很显然，这样的解释是不够的，因此我们证明这是真的。

让我们分两个阶段证明等式7的结论的真实性。 首先，我们证明所得速度矢量的值是正确的； 然后-他的方向是正确的。 对于证明的第一部分，请考虑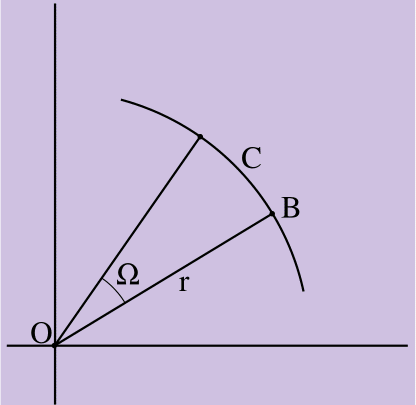图2。



图2. C =Ωr

图2显示了B点沿刚体旋转方向以Ω弧度旋转的角度，其半径矢量为从体O的旋转中心到B点的长度为r.B通过了圆弧C的长度，其中C =Ωr，以弧度表示。 （角度的弧度是指以圆的半径为边界的弧的量度。由于圆弧的弧度是2π[或360度]，所以圆的周长为C =2πr）。

点的速度是其时间坐标的变化。 因此，我们可以通过相对于时间微分运动方程来找到B点的速度，换句话说，就是速度矢量的大小。 C =Ωr是运动方程。

$$

$${d（Ωr）\ over {dt}} = {dΩ\ over {dt}} r =ωr$$

半径从微分符号中减去，因为它是一个常数（点B只是旋转，没有线性运动），并且时间导数Ω是根据等式6的ω。因此，向量B的大小为速度向量ωr。

通过考虑方程式7，我们注意到速度矢量的大小是正确的，因为垂直线不影响矢量的长度，并且r ^ OB是从O指向B的半径矢量。

为了验证公式7中的速度矢量的方向正确，让我们从确保速度矢量必须垂直于半径矢量开始。 这个假设是直观可理解的，因为围绕某个其他给定点旋转的点只能垂直于这些点之间的向量移动。 它不能接近或远离旋转中心，否则该运动将不再是旋转。 我们可以通过向量的计算来支持我们的假设，但是对于本文的篇幅，我受制于一定的框架，因此我们将假设我们的假设是正确的。 （如果您渴望自己证明这一点，请自己区分固定长度向量的标量积。）

最后，我们必须确保正确标记矢量，因为该图显示了两个垂直于半径的长度相等的矢量：v和-v。 因为Ω的值是逆时针测量的，所以当点顺时针旋转时ω> 0。 垂直点以及半径向量都指向顺时针方向。 图3显示了公式7的结论：



图3.线速度和角之间的关系

补充方程式7以描述运动物体的旋转。 我们将实体的运动视为围绕该点的身体旋转中心的简单运动和身体其余部分的简单旋转。 对于那些感兴趣的人，这是关于运动分类的沙尔定理。

查尔定理将我们的运动分为线性和角度两个部分。 令物体O的旋转中心为唯一的移动点，然后使用ω计算绕点O的旋转，这使我们得到了等式7的一般形式：

$$$$显示$$ v ^ B = v ^ O +ωr^ {OB}_⟂$$显示$$

式9

公式9表示，我们可以使用物体旋转中心的线性速度以及在物体旋转过程中获得的速度来计算运动物体任何点的速度。

我们冲动的原因

现在我们可以写出等式2的角度类似物，即力的等式。 我们从确定给定点B围绕另一个点A的角动量L ^ AB开始：

$$

$${L} ^ {AB} = {\ vec r} ^ {AB} \次{\ vec p} ^ B$$

式10

点的动量矩与点的线性动量的不同之处在于，方程的角度形式考虑了物体在空间中的位置。 由此得出结论，与为给定点（其质量和速度的乘积）确定的线性脉冲相反，必须为游戏世界中的另一个位置测量点的角动量。 这通过等式10中的较高索引显示。符号L ^ AB表示从点A（物体的旋转中心）为点B测量了角动量。 想象一个箭头，该箭头从A点指向B点。该箭头是两点之间的半径向量，它表示r ^ AB。 因此，一个点的角动量是线性动量向量和垂直于该点的半径向量的标量积。 此操作称为“垂直标量积”，是3D矢量积的2D模拟，但我们将在下一次讨论。

如果您在纸上以图形方式描述方程10的结果，就像我在图4中所做的那样，您将看到它确定了点B的线性矩如何“绕” A旋转的度量。



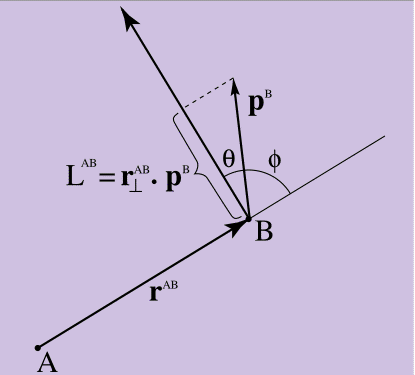图4.冲动的时刻

如果点B的动量直接指向点A，则等式10 = 0（因为与r垂直的直线与p形成直角，并且标量积为0），一切都正确。 垂直于A的动量B越大，动量越大。 从图4中可以看出，公式10中的标量积的参数r包含在垂直r ^ AB与p ^ B之间的夹角θ的余弦。 另一方面，标量乘积的大小由原始的，而不是垂直的r ^ AB与p ^ B之间的角度φ的正弦给出（正弦是解开向量与标量积之间关系的另一个关键）。 公式10给出了相对于点A，点B在“旋转方向”上“看”多少动量的度量。

同样，当我们使用线性动量的导数来确定力时，我们将使用角动量的导数来确定力的角孪生力-力矩（用小写字母tau-τ表示）。

$$

$$τ^ {AB} = {dL ^ {AB} \ over dt} = {d（{\ vec r} ^ {AB} \倍{\ vec p} ^ B）\ over dt} = \ vec r ^ { AB} \乘以ma ^ B = \ vec r ^ {AB} \乘以F ^ B$$

式11

为了节省空间，我在等式11中作了一点欺骗，跳过了一些涉及寻找导数的困难步骤。 根据前述内容，可以得出力的力矩与通过标量积在特定点处的力相关联。

最后，我们得到了一个使用力施加点的动力学方程，该动力学方程先前在线性动量方程中被忽略。 公式11使用具有垂直方向的标量积来度量施加到点B的力有多少围绕点A旋转； 这种“旋转力”被称为力矩。 公式11使您能够找到力矩的数值，从而求出角动量，如果我们对力矩进行积分，则知道所施加的力和作用点。

但是，我们仍未收到力矩与运动所需的绕其轴旋转的运动学角度大小之间的关系方程式，例如角加速度，角速度或方向。 因此，我们无法继续推导更多的方程式。

我们都在等待的时刻

在动力学和运动学之间建立联系之前，我们需要类似于在公式4中确定总线性动量的方式来确定总角动量。我没有忘记方程3中质心的等效角。 我们将在总角动量方程中看到它。

点A附近的总角动量由L ^ AT表示，由公式12确定：

$$

$$L ^ {AT} = {\ sum _ {i} {} {\ vec r ^ {Ai} \ times p ^ i}} = {\ sum _ {i} {\ vec r ^ {Ai} \ times m ^ iv ^ i}}$$

式12

等式12是相对于点A测得的人体所有点的所有角力矩的总和。在右侧，我使用线性动量的定义以便将p ^ i表示为质量与速度（mv）的乘积。 将来对我来说将很有用，以便根据等式12制作出具有更明显应用特性的东西。 该方程式说，要找到我们物体的总角动量，必须将其所有点的角动量求和。 对于包含面（而不是来自不同点）的实体，有必要针对非离散和计算积分。

幸运的是，我们可以通过引入一个称为“惯性矩”的新量来简化计算，类似于我们引入质心来简化总动量方程式的方式。回想一下，由于方程式7，我们可以通过角速度找到点的速度。假设公式12中的点A是公式7的旋转中心，公式12中的总索引i是公式7的点B，则可以将公式7转换为公式12。我们得到：

$$

$$L^{AT} = \sum _{ i} {\vec r ^{Ai} \times m^i ω \vec r^{Ai}} = ω {\sum _{ i} {m^i \vec r^{Ai} \times \vec r ^{Ai}}} = ω \sum_{ i} {m^i (\vec r ^{Ai})^2} = ωI^A$$

公式13我将

逐步详细记录公式13。首先，我们用12代替等式7，以便得到等式13中的总和。这种替换使我们能够使用角速度描述角动量。接下来，我们将ω作为总和，因为它对于实体的所有点都是相等的（角速度是为整个身体确定的，而不是分别为每个点确定的），并记下左侧带有索引i的质量，以便更清楚地看到标量积半径自己的矢量。此标量乘积等于半径矢量的长度的平方（任何矢量本身的标量乘积=其长度的平方。请记住，垂直算子不会更改矢量的长度。）。最后，我们写出I ^ A，以表示围绕点A的惯性矩。

二维实体的惯性矩是一个非常好的数，因为组成物体的这些点不能改变其质量或移动离开旋转中心。由于这两个属性，公式13中的和对于每个物体都是一个常数，因此我们可以对其进行计算。用俄语说，I ^ A是从点A到人体所有其他点的距离的平方和，并且每个这样的距离根据每个点的质量进行缩放。就像质心一样-如果实体比由离散点组成的实体更坚固，则总和将变成积分。惯性矩的大小将保持不变，并且具有相同的物理含义。

确定某个点附近的惯性矩很冗长，但可以将I ^ A看作是使身体绕点A旋转的难易程度的度量。例如，想象一下一支铅笔（扁平铅笔）。如果我们测量铅笔中心附近的惯性矩，我们将得到一个等于根据每个点的质量缩放的距离的平方和的某个值。而如果我们在同一根铅笔的笔尖上测量惯性，则会得到一个更大的值，因为质量被删除的点越远，其距离平方的值就越大。在这里，我们将用数学的方式来表达对我们直观的内容：绕着铅笔的中心旋转铅笔比绕着一支铅笔的末端旋转铅笔要容易得多（省力）。

最后，我们准备在动力学的角度方程和运动学的角度方程之间建立联系。如果我们对方程式13求微分，则左侧得到的是总力矩，而右边则是惯性矩与角加速度的乘积（I ^ A是一个常数，我们将其置于微分符号之外）：

$$

$$τ^{AT} = {dL^{AT} \over dt} = {d( I^A ω) \over dt} = I^A ω = I^A α$$

公式14

该公式与公式5等效。实际上，对于角动力学，它为F = ma。这是通过标量惯性矩将总力矩与车身角加速度联系起来的方程式。如果我们知道施加在身体上的力矩，就可以找到它的角加速度，然后通过积分求出空间中的角速度和方向-用力矩除以惯性矩。

动力学算法

他几乎没有通过方程式的旋涡看到我们，但是所有这些都是方程式的组成部分。我们已经推导了足够的方程来获得二维世界的宏伟动态，其中具有任意给定的力和移动和旋转物体的力的力矩。如何使用这些方程式？下面是基本算法：

1. 求出质心的值和质心的惯性矩。
2. 设置物体的初始坐标，其在空间中的方向，其线性和角速度。
3. 考虑所有作用在身体上的力及其应用要点。
4. 求出所有力的合力，然后将其除以物体的质量，以求出质心的线性加速度（公式5）。
5. , , , ( 11).
6. ( 14).
7. , , ( ).
8. , 3.

在上面的算法中，只有两个步骤我没有解释。首先，如何计算步骤1中的固体物体的惯性矩？其次，如何用步骤3中的力解决问题？第一个问题的答案可以在一个简单的代码示例中找到，我将在本文结尾处将其留在应用程序中（您将按对象的区域对对象进行集成）。许多关于动力学的书最后都包含了应用程序中经常遇到的物体形式的惯性矩的计算，因此您不必每次都自己显示它们。

关于如何计算第3步中的力的问题的答案取决于应用程序，但是我将给出一些一般性建议。首先，诸如重力之类的力始终指向一个方向（在重力情况下为向下），不会产生力矩，因为它们在同一时间同时拉动所有点，尽管我们我们将这些力直接施加到质心。类似于弹力的力会施加到物体的某个点，它们会产生一个力矩，因此我们在一般情况下考虑它们。正如我们在第一篇文章中看到的那样，摩擦力是与物体的速度相反的方向上的相同力。

您可以制作一个简单的物理模型来展示摩擦力，然后将力施加到质心，或者选择对象的哪些部分将施加摩擦力，然后执行此操作，这会产生作用在物体上的力矩。物体在碰撞中所受的力要困难一些，我们将在下一篇文章中了解它们。应该将像火箭发动机推力之类的力视为具有作用点的力（在这种情况下，如果其中一台发动机发生故障，您将开始绕其轴旋转，直到您调整方向盘以平衡力力矩为止！）。如果您想要类似UFO的重力射线，则应将此力计算为重力，而不要产生力矩，或者应将其应用于对象上的特定点，上升时会围绕这一点旋转吗？选择是您的。关键是不要害怕尝试以不同方式计算的不同力，因为现在您有了一个真正的二维图形模拟器，可以尝试不同类型的力！

我将所有需要的代码和链接留在了我的网站上，因为没有更多空间了。在我的简单应用程序中，我实现了二维世界动力学的算法，还添加了通过弹簧固定的对象；它们绕其轴旋转，有时甚至与墙壁碰撞并旋转。但我会再谈一次。单击链接获取更多文献，以及适用于Windows 32和Macintosh的简单应用程序。

克里斯·赫克（Chris Hecker）很少遇到惯性矩的影响，但通常很快就会过去。可以将力施加到checker@bix.com。

译者的注释：这里有一个双关语，文章的主题及其内容都会显示出来。

PS欢迎反馈。您的评论可以提高工作质量。谢谢你

PPS翻译的作者特别感谢berez和Vasily Tereshkov的用户编辑了翻译。谢谢你