自适应天线阵列：如何工作？ （基本）

大家好

最近几年，我致力于研究和创建用于自适应天线阵列中信号空间处理的各种算法，并且作为我目前工作的一部分，我将继续这样做。 在这里，我想分享我发现的知识和芯片。 我希望这对开始研究信号处理领域或只是感兴趣的人们有用。

什么是自适应天线阵列？

天线阵列是一组天线元件，以某种方式布置在空间中。 为了简化自适应天线阵列的结构，我们将考虑采用以下形式表示：


自适应天线阵列通常称为“智能天线”（ Smart Antennas）。 “智能”天线阵列由空间信号处理单元及其中实现的算法组成。 这些算法分析接收到的信号并形成一组权重$$ $ inline $ w_1 ... w_N $ inline $ 它确定每个元素的信号幅度和初始相位。 给定的幅度相位分布确定了整个晶格整体的方向性模式 。 合成所需形状的辐射方向图并在信号处理期间对其进行更改的能力是自适应天线阵列的主要特征之一，它可以解决各种各样的问题 。 但是首先是第一件事。

辐射图是如何形成的？

辐射图表征了沿特定方向辐射的信号的功率。 为简单起见，我们将晶格元素各向同性，即 对于每个信号，发射信号的功率不取决于方向。 由于天线阵列的各个元件发射的 电磁波的干扰，获得了在特定方向上由阵列辐射的功率的放大或衰减。 仅当EMW 相干 （即 信号的相位差不应随时间变化。 在理想情况下，天线阵列的每个元件应以相同的载波频率发射谐波信号$$ $内联$ f_ {0} $内联$ 。 然而，实际上，有必要使用具有有限宽度频谱的窄带信号$$ $ inline $ \ Delta f << f_ {0} $ inline $ 。
让所有AR元件发出具有复振幅的相同信号$$ $内联$ x_n（t）= u（t）$内联$ 。 然后，在远程接收器处，可以从第n个元素接收的信号以解析形式表示：

$$$$显示$$ a_n（t）= u（t- \ tau_n）e ^ {i2 \ pi f_0（t- \ tau_n）} $$显示$$

在哪里$$ $内联$ \ tau_n $内联$ -从天线元件到接收点的信号传播延迟。
这样的信号是“准谐波”，并且为了满足相干条件，任何两个元素之间的电磁波传播的最大延迟必须远小于信号包络变化的特征时间。$$ $内联$ T $内联$ ，即$$ $ inline $ u（t- \ tau_n）≈u（t- \ tau_m）$ inline $ 。 因此，窄带信号的相干性条件可以写为：

$$$$ display $$T≈\ frac {1} {\ Delta f} >> \ frac {D_ {max}} {c} = max（\ tau_k- \ tau_m）$$ display $$

在哪里$$ $ inline $ D_ {max} $ inline $ -AR元素之间的最大距离，并且$$ $ inline $和$ inline $ 是光速。

当接收信号时，在空间处理单元中以数字方式执行相干求和。 在这种情况下，该块输出处的数字信号的复数值由以下表达式确定：

$$$$显示$$ y = \ sum_ {n = 1} ^ Nw_n ^ * x_n $$显示$$

以矩阵形式的 N维复矢量的标量积形式表示最后一个表达式更加方便：

$$$$ display $$ y =（\ textbf {w}，\ textbf {x}）= \ textbf {w} ^ H \ textbf {x} $$ display $$

其中w和x是列向量，并且$$ $ inline $（。）^ H $ inline $ -Hermitian配对的运算。

信号的矢量表示是使用天线阵列的基本方法之一，因为 通常避免繁琐的数学计算。 另外，利用向量对在某个时刻接收到的信号进行识别通常可以使我们从真实的物理系统中抽象出来，并从几何学的角度理解发生了什么。

为了计算天线阵列的方向性图，有必要在思维上始终如一地“运行”来自所有可能方向的一组平面波 。 在这种情况下，向量x的元素值可以表示如下：

$$$$显示$$ x_n = s_n = \ exp \ {-i（\ textbf {k}（\ phi，\ theta），\ textbf {r} _n）\} $$显示$$

其中k是波矢$$ $内联$ \ phi $内联$ 和$$ $内联$ \ theta $内联$ -表征平面波到达方向的方位角和仰角 ，$$ $ inline $ \ textbf {r} _n $ inline $ -天线元件的坐标，$$ $内联$ s_n $内联$ -具有波矢量k 的平面波的相位矢量s的元素（在英语文献中，相位矢量称为转向矢量）。 y的振幅平方对$$ $内联$ \ phi $内联$ 和$$ $内联$ \ theta $内联$ 对于权重系数w的给定向量，确定接收时天线阵列的方向性图。

天线阵列的特征

在水平平面上研究线性等距天线阵列上天线阵列辐射方向图的一般特性非常方便（即波束方向图仅取决于方位角$$ $内联$ \ phi $内联$ ） 从两个角度来看，它很方便：分析计算和可视化表示。

我们计算单位重量向量的DN（$$ $内联$ w_n = 1，n = 1 ... N $内联$ ），遵循上述方法。


结果，我们得到：

$$$$ display $$ F（\ phi）= | y | ^ 2 = \ frac {\ sin ^ 2（\ pi \ frac {Nd} {\ lambda} \ sin \ phi）} {\ sin ^ 2（\ pi \ frac {d} {\ lambda} \ sin \ phi）} $$显示$$

辐射图频率

天线阵列的最终辐射方向图是角度正弦的周期函数。 这意味着对于d /λ比的某些值，它具有衍射（附加）最大值。
N = 5时的非归一化天线方向图
极坐标系中N = 5时天线阵列的归一化辐射方向图

可以从NAM 公式直接查看“衍射主义者”的位置。 但是，我们将尝试了解它们的物理和几何来源（在N维空间中）。

相位向量s的元素是复指数$$ $ inline $ e ^ {i \ Psi n} $ inline $ 其值由广义角度的值确定$$ $ inline $ \ Psi = 2 \ pi \ frac {d} {\ lambda} \ sin \ phi $内联$ 。 如果存在两个对应于平面波到达方向不同的广义角，$$ $内联$ \ Psi_1 = \ Psi_2 + 2 \ pi m $内联$ ，则意味着两件事：

• 物理上：来自这些方向的平面波前会在天线阵列的元件上感应出相同的电磁波振幅相位分布。
• 在几何上：这两个方向的相位矢量是重合的。

从天线阵列的角度来看，以类似方式连接的波到达方向是等效的，并且彼此无法区分。

如何确定仅MD的一个主要最大值始终位于的角度区域？ 由于以下原因，我们将在零方位角附近执行此操作：两个相邻元素之间的相移应位于从$$ $ inline $-\ pi $ inline $ 之前$$ $内联$ \ pi $内联$ 。

$$$$ display $$-\ pi <2 \ pi \ frac {d} {\ lambda} \ sin \ phi <\ pi $$ display $$

解决这个不等式，我们得到零附近的唯一性区域的条件：

$$$$显示$$ | \ sin \ phi | <\ frac {\ lambda} {2d} $$显示$$

可以看出，角度唯一区域的大小取决于比率d /λ 。 如果d = 0.5λ ，则信号的每个到达方向都是“个体”，并且唯一性区域会覆盖整个角度范围。 如果d = 2.0λ ，则方向0，±30，±90是等效的。 衍射波瓣出现在辐射图上。

通常，衍射波瓣倾向于使用定向天线元件来抑制。 在这种情况下，天线阵列的完整辐射方向图是一个元件的方向图和各向同性元件的阵列的乘积。 通常根据天线阵列的唯一性区域上的条件来选择一个元素的DN参数。

主瓣宽度

估算天线系统主瓣宽度的工程公式是众所周知的 ：$$ $ inline $ \ Delta \ phi≈\ frac {\ lambda} {D} $ inline $ 其中D是天线的特征尺寸。 该公式用于各种类型的天线，包括SLR天线。 我们证明它对于天线阵列也是有效的。

我们通过主最大值附近的MD的第一个零来确定主瓣的宽度。 的分子表达$$ $内联$ F（\ phi）$内联$ 消失在$$ $ inline $ \ sin \ phi = m \ frac {\ lambda} {dN} $ inline $ 。 第一个零对应于m =±1。 假设$$ $ inline $ \ frac {\ lambda} {dN} << 1 $ inline $ 我们得到$$ $ inline $ \ Delta \ phi = 2 \ frac {\ lambda} {dN} $ inline $ 。

通常，方向性波束宽度AR由半功率电平（-3 dB）确定。 在这种情况下，请使用表达式：

$$$$显示$$ \ Delta \phi≈0.​​88\ frac {\ lambda} {dN} $$显示$$

通过为天线阵列的权重系数设置不同的振幅值，可以控制主瓣的宽度。 考虑三个分布：

• 均匀振幅分布（权重1）：$$ $内联$ w_n = 1 $内联$ 。
• 幅度值下降到晶格的边缘（权重2）：$$ $ inline $ w_n = 0.5 + 0.3 \ cos（2 \ pi \ frac {n-1} {N}-\ pi \ frac {N-1} {N}）$ inline $
• 幅度值增加到光栅的边缘（权重3）：$$ $ inline $ w_n = 0.5-0.3 \ cos（2 \ pi \ frac {n-1} {N}-\ pi \ frac {N-1} {N}）$ inline $

该图以对数刻度显示了所得的归一化辐射方向图：
从图中可以观察到以下趋势：朝着晶格边缘减小的权重系数的幅度分布导致MD的主瓣变宽，但旁瓣的水平减小。 相反，朝向天线阵列的边缘增加的幅度导致主瓣变窄并且侧面的水平增加。 在这里考虑限制情况很方便：

1. 除极端元素外，所有元素的加权系数幅度均等于零。 极端元素的权重等于1。 在这种情况下，晶格等于周期为D =（N-1）d的两元素AR。 根据以上公式估算主瓣的宽度并不难。 在这种情况下，支管将变成衍射最大值并与主最大值对齐。
2. 中心元素的权重等于1，其余所有权重等于0。 在这种情况下，我们基本上得到了一个具有各向同性辐射方向图的天线。

主要最大值的方向

因此，我们研究了如何调整AP AR主瓣的宽度。 现在，让我们看看如何引导方向。 调用接收信号的矢量表达式 。 假设我们要让最大辐射图朝某个方向看$$ $内联$ \ phi_0 $内联$ 。 这意味着应从该方向获取最大功率。 相位矢量对应于该方向$$ $ inline $ \ textbf {s}（\ phi_0）$ inline $ 在N维向量空间中，接收功率定义为该相位向量的标量乘以权重系数w的向量的平方。 当两个向量共线时 ，即两个向量的标量积最大。$$ $ inline $ \ textbf {w} = \ beta \ textbf {s}（\ phi_0）$ inline $ ，其中β是一些归一化因子。 因此，如果我们选择所需方向的权重向量等于相位向量，则将旋转最大辐射方向图。

以以下权重为例：$$ $ inline $ \ textbf {w} = \ textbf {s}（10°）$ inline $

$$$$ display $$ w_n = \ exp \ {i2 \ pi \ frac {d} {\ lambda}（n-1）\ sin（10 \ pi / 180）\} $$ display $$

结果，我们获得了在10°方向上具有最大最大值的辐射图。

现在我们应用相同的权重，但不用于信号接收，而是用于传输。 在此值得考虑的是，在发送信号时，波矢量的方向相反。 这意味着用于接收和发送的相位矢量的元素在指数上的符号不同，即 通过复杂的共轭相互联系。 结果，我们在-10°方向上获得了辐射方向图的最大值，这与相同权重系数下的接收信号的最大值不一致。要纠正这种情况，还必须对权重系数应用复共轭。

在使用天线阵列时，应始终牢记所描述的用于接收和发射的波束的特征。

让我们玩一下辐射图

几高

我们提出的问题是在方向上形成辐射图的两个主要最大值：-5°和10°。 为此，我们选择相应方向的相位矢量的加权和作为加权矢量。

$$$$显示$$ \ textbf {w} = \ beta \ textbf {s}（10°）+（1- \ beta）\ textbf {s}（-5°）$$显示$$

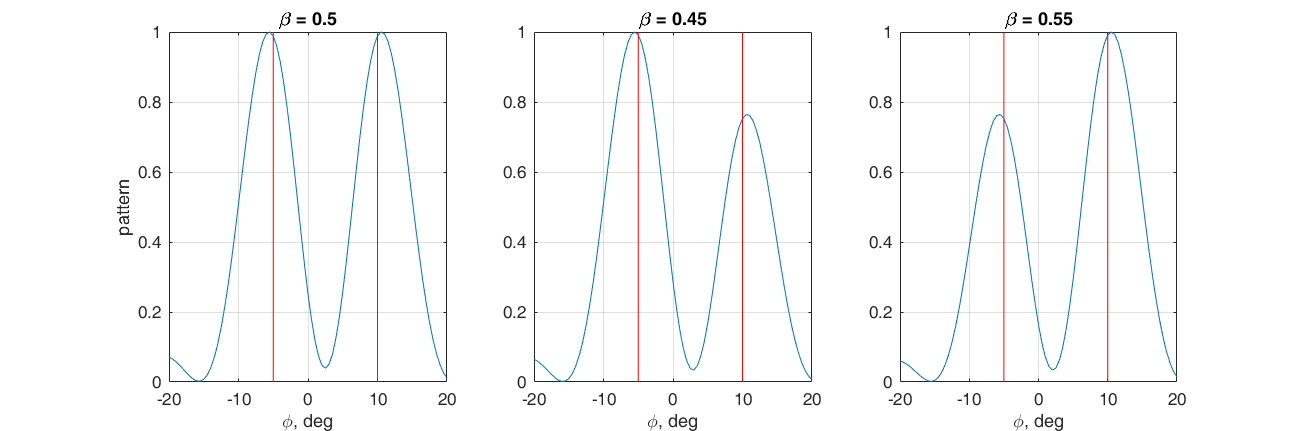
通过调节系数β ，可以调节主瓣之间的比率。 同样，这里很方便地查看向量空间中正在发生的事情。 如果β大于0.5，则权重向量更接近s （10°），否则更接近s （-5°）。 权重向量越靠近相量之一，则相应的标量积越大，因此ND的相应最大值的幅度也越大。

但是，值得考虑的是，两个主瓣都具有有限的宽度，如果我们要在两个接近的方向上进行调谐，则这些瓣将合并为一个，朝向某个中间方向。

一最大值零

现在让我们尝试将最大辐射图调整到$$ $ inline $ \ phi_1 = 10°$ inline $ 同时抑制来自方向的信号$$ $ inline $ \ phi_2 = -5°$ inline $ 。 为此，必须将相应角度设置为零。 您可以按照以下步骤进行操作：

$$$$ display $$ \ textbf {s} = \ textbf {s} _1- \ frac {\ textbf {s} _2 ^ H \ textbf {s} _1} {N} \ textbf {s} _2 $$ display $$

在哪里$$ $ inline $ \ textbf {s} _1 = \ textbf {s}（10°）$ inline $ 和$$ $ inline $ \ textbf {s} _2 = \ textbf {s}（-5°）$ inline $ 。

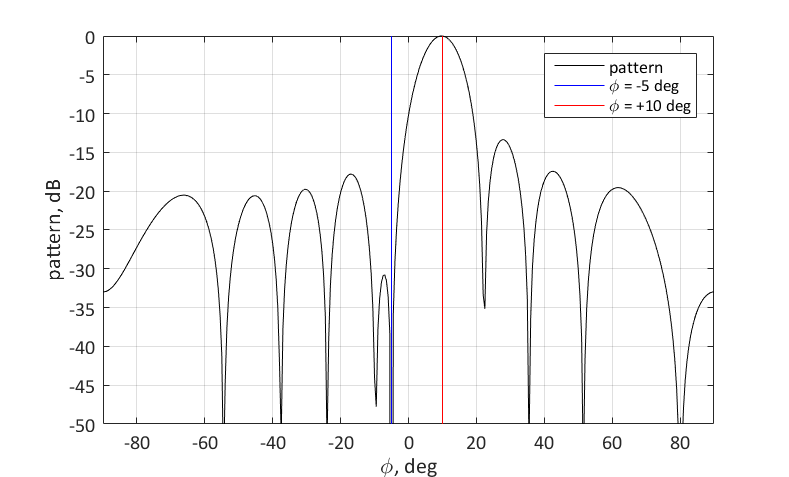
选择权重向量的几何意义如下。 我们希望向量w在上具有最大投影$$ $ inline $ \ textbf {s} _1 $ inline $ 并且与向量正交$$ $ inline $ \ textbf {s} _2 $ inline $ 。 向量$$ $ inline $ \ textbf {s} _1 $ inline $ 可以表示为两个术语：共线向量$$ $ inline $ \ textbf {s} _2 $ inline $ 和正交向量$$ $ inline $ \ textbf {s} _2 $ inline $ 。 为了满足问题陈述，有必要选择第二分量作为权重系数w的向量。 共线分量可以通过设计矢量来计算$$ $ inline $ \ textbf {s} _1 $ inline $ 归一化向量$$ $ inline $ \ frac {\ textbf {s} _2} {\ sqrt {N}} $ inline $ 使用标量产品。

$$$$ display $$ \ textbf {s} _ {1 ||} = \ frac {\ textbf {s} _2} {\ sqrt {N}} \ frac {\ textbf {s} _2 ^ H \ textbf {s} _1} {\ sqrt {N}} $$显示$$

因此，从初始相位矢量中减去$$ $ inline $ \ textbf {s} _1 $ inline $ 它的共线分量，我们获得所需的权重向量。

一些附加说明

1. 在上面的所有地方，我都省略了归一化权重向量的问题，即 它的长度。 因此，权重向量的归一化不会影响天线阵列辐射方向图的特性：主最大值的方向，主瓣的宽度等。 还可以表明，这种归一化不会影响空间处理块输出处的SNR 。 在这方面，当考虑空间信号处理算法时，我通常接受加权向量的单位归一化，即$$ $ inline $ \ textbf {w} ^ H \ textbf {w} = 1 $ inline $
2. 形成天线阵列底部的可能性由元件的数量N决定。元件越多，可能性就越大。 在空间权重处理的实现中，自由度越高，如何在N维空间中“扭曲”权重矢量的选择就越多。
3. 当接收天线波束方向图时，天线阵列实际上并不存在，而所有这些仅存在于处理信号的计算单元的“成像”中。 这意味着，可以同时合成多个MD，并独立处理从不同方向到达的信号。 在传输的情况下，一切都有些复杂，但是也可以合成几个MD来传输各种数据流。 通信系统中的这项技术称为MIMO 。
4. 使用提供的Matlab代码，您可以自己玩NAM
   
   代号

   % antenna array settings N = 10; % number of elements d = 0.5; % period of antenna array wLength = 1; % wavelength mode = 'receiver'; % receiver or transmitter % weights of antenna array w = ones(N,1); % w = 0.5 + 0.3*cos(2*pi*((0:N-1)-0.5*(N-1))/N).'; % w = 0.5 - 0.3*cos(2*pi*((0:N-1)-0.5*(N-1))/N).'; % w = exp(2i*pi*d/wLength*sin(10/180*pi)*(0:N-1)).'; % b = 0.5; w = b*exp(2i*pi*d/wLength*sin(+10/180*pi)*(0:N-1)).' + (1-b)*exp(2i*pi*d/wLength*sin(-5/180*pi)*(0:N-1)).'; % b = 0.5; w = b*exp(2i*pi*d/wLength*sin(+3/180*pi)*(0:N-1)).' + (1-b)*exp(2i*pi*d/wLength*sin(-3/180*pi)*(0:N-1)).'; % s1 = exp(2i*pi*d/wLength*sin(10/180*pi)*(0:N-1)).'; % s2 = exp(2i*pi*d/wLength*sin(-5/180*pi)*(0:N-1)).'; % w = s1 - (1/N)*s2*s2'*s1; % w = s1; % normalize weights w = w./sqrt(sum(abs(w).^2)); % set of angle values to calculate pattern angGrid_deg = (-90:0.5:90); % convert degree to radian angGrid = angGrid_deg * pi / 180; % calculate set of steerage vectors for angle grid switch (mode) case 'receiver' s = exp(2i*pi*d/wLength*bsxfun(@times,(0:N-1)',sin(angGrid))); case 'transmitter' s = exp(-2i*pi*d/wLength*bsxfun(@times,(0:N-1)',sin(angGrid))); end % calculate pattern y = (abs(w'*s)).^2; %linear scale plot(angGrid_deg,y/max(y)); grid on; xlim([-90 90]); % log scale % plot(angGrid_deg,10*log10(y/max(y))); % grid on; % xlim([-90 90]); 

   
   

借助自适应天线阵列可以解决哪些任务？

谢谢您的关注。